Riemannsche Vermutung: Unterschied zwischen den Versionen
K |
|||
| (12 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 69: | Zeile 69: | ||
Im Fall <math> f(s) = 1 </math> ist dies gleich der Zeta-Funktion, und es gilt | Im Fall <math> f(s) = 1 </math> ist dies gleich der Zeta-Funktion, und es gilt | ||
| − | :<math>\displaystyle \zeta (s) = \prod _{p ~\text{prim}} \sum_{k = 0}^\infty \frac{1}{p^{ks}}</math> für <math>\text{Re}(s) > 1 </math>. | + | :<math>\displaystyle \zeta (s) = \prod _{p ~\text{prim}} \sum_{k = 0}^\infty \frac{1}{p^{ks}}~~~</math> für <math>\text{Re}(s) > 1 </math>. |
Da jede Summe eine geometrische Reihe mit Quotient <math> p^{-s} </math> bildet, folgt | Da jede Summe eine geometrische Reihe mit Quotient <math> p^{-s} </math> bildet, folgt | ||
| − | :<math>\displaystyle \zeta (s) = \prod _{p \text{ prim}} \frac{1}{1- \frac{1}{p^s}} </math> für <math>s \in \mathbb{C}, \text{Re}(s) > 1 </math>. | + | :<math>\displaystyle \zeta (s) = \prod _{p \text{ prim}} \frac{1}{1- \frac{1}{p^s}}~~~ </math> für <math>s \in \mathbb{C}, \text{Re}(s) > 1 </math>. |
| Zeile 92: | Zeile 92: | ||
:<math>\displaystyle | :<math>\displaystyle | ||
| − | \zeta (s) = \frac{1}{\Gamma (s)} \left( \frac{1}{s-1} \frac{1}{2s} \sum_{n=2}^\infty \frac{B_n}{n!} \frac{1}{s + n -1} + \int_1 ^\infty \frac{x^{s-1}}{e^x-1} \right) | + | \zeta (s) = \frac{1}{\Gamma (s)} \left( \frac{1}{s-1} \frac{1}{2s} \sum_{n=2}^\infty \frac{B_n}{n!} \frac{1}{s + n -1} + \int_1 ^\infty \frac{x^{s-1}}{e^x-1} \right) ~~~ |
| − | </math> | + | </math> für <math>s \in \mathbb{C} \backslash \{ 1\} </math> |
Eine Herleitung und weiterführende Informationen | Eine Herleitung und weiterführende Informationen | ||
| Zeile 118: | Zeile 118: | ||
Um den Verlauf der bereits erwähnten Primzahlfunktion <math> \pi (x) </math> abzuschätzen, eignet sich der Primzahlsatz, der dafür eine konkrete Näherungsfunktion angibt: | Um den Verlauf der bereits erwähnten Primzahlfunktion <math> \pi (x) </math> abzuschätzen, eignet sich der Primzahlsatz, der dafür eine konkrete Näherungsfunktion angibt: | ||
| − | :<math>\displaystyle \lim _{{x\to \infty }}{\frac {\pi (x)}{{\frac {x}{\ln(x)}}}}=1</math> , also <math>\displaystyle \pi (x) \sim \frac{x}{\ln {x}} </math> | + | :<math>\displaystyle \lim _{{x\to \infty }}{\frac {\pi (x)}{{\frac {x}{\ln(x)}}}}=1~~</math>, also <math>\displaystyle \pi (x) \sim \frac{x}{\ln {x}} </math> |
: (<math>\sim</math> bedeutet "asymptotisch äquivalent", d.h. die Abschätzung wird prozentual immer genauer) | : (<math>\sim</math> bedeutet "asymptotisch äquivalent", d.h. die Abschätzung wird prozentual immer genauer) | ||
| Zeile 135: | Zeile 135: | ||
Die Zeta-Funktion hängt über ihre Produktschreibweise direkt mit den Primzahlen zusammen: | Die Zeta-Funktion hängt über ihre Produktschreibweise direkt mit den Primzahlen zusammen: | ||
| − | :<math>\displaystyle \zeta (s)=\prod _{p\ {\text{prim}}}{\frac {1}{1-{\frac {1}{p^{s}}}}}</math> | + | :<math>\displaystyle \zeta (s)=\prod _{p\ {\text{prim}}}{\frac {1}{1-{\frac {1}{p^{s}}}}}~~~</math>für <math>\text{Re}(s)>1</math> |
Diese zweite Form der Zeta-Funktion lässt sich umwandeln in eine Formel für <math>\ln {\zeta(s)}</math> : | Diese zweite Form der Zeta-Funktion lässt sich umwandeln in eine Formel für <math>\ln {\zeta(s)}</math> : | ||
| Zeile 151: | Zeile 151: | ||
Dieser Ausdruck lässt sich über eine inverse Mellin-Transformation ([https://de.wikipedia.org/wiki/Mellin-Transformation siehe Wikipedia]) "umkehren" zu: | Dieser Ausdruck lässt sich über eine inverse Mellin-Transformation ([https://de.wikipedia.org/wiki/Mellin-Transformation siehe Wikipedia]) "umkehren" zu: | ||
| − | :<math>{\displaystyle \Pi (x)={\frac {1}{2\pi i}}\int \limits _{c-i\infty }^{c+i\infty }{\frac {\ln \zeta (s)}{s}}x^{s}\mathrm {d} s}</math> | + | :<math>{\displaystyle \Pi (x)={\frac {1}{2\pi i}}\int \limits _{c-i\infty }^{c+i\infty }{\frac {\ln \zeta (s)}{s}}x^{s}\mathrm {d} s}~~~</math> mit einem <math> c>1 </math><math>~~~(*)</math> |
Eine weitere von Riemann eingeführte Funktion, die Riemannsche Xi-Funktion, benutzt in ihrer Produktdarstellung alle nicht-trivialen Nullstellen <math>\rho</math> der Zeta-Funktion: | Eine weitere von Riemann eingeführte Funktion, die Riemannsche Xi-Funktion, benutzt in ihrer Produktdarstellung alle nicht-trivialen Nullstellen <math>\rho</math> der Zeta-Funktion: | ||
| Zeile 160: | Zeile 160: | ||
:<math>{\displaystyle \ln \zeta (s)=\sum _{\rho }\ln \left(1-{\frac {s}{\rho }}\right)-\ln 2-\ln \Gamma \left(1+{\frac {s}{2}}\right)+{\frac {s}{2}}\ln \pi -\ln(s-1)}</math> | :<math>{\displaystyle \ln \zeta (s)=\sum _{\rho }\ln \left(1-{\frac {s}{\rho }}\right)-\ln 2-\ln \Gamma \left(1+{\frac {s}{2}}\right)+{\frac {s}{2}}\ln \pi -\ln(s-1)}</math> | ||
| − | Indem man <math>\ln {\zeta(s)}</math> in der Gleichung <math> | + | Indem man <math>\ln {\zeta(s)}</math> in der Gleichung <math>(*)</math> durch obigen Ausdruck substituiert, erhält man (was nochmals einige Arbeit vonseiten Riemanns erforderte) letztendlich eine Formel für <math>\Pi (x)</math>, in der über alle nicht-trivialen Nullstellen <math> \rho </math> der Zeta-Funktion summiert wird: |
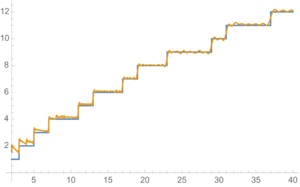
[[Datei:Li angenaehrt.png|mini|Je mehr Nullstellen der Zeta-Funktion eingesetzt werden, desto besser nähert sich die Vorhersage (gelb) der Primzahlfunktion (blau) an.]] | [[Datei:Li angenaehrt.png|mini|Je mehr Nullstellen der Zeta-Funktion eingesetzt werden, desto besser nähert sich die Vorhersage (gelb) der Primzahlfunktion (blau) an.]] | ||
:<math>{\displaystyle \Pi (x)=\mathrm {Li} (x)-\sum _{\rho }\mathrm {Li} (x^{\rho })-\ln 2+\int \limits _{x}^{\infty }{\frac {\mathrm {d} t}{t(t^{2}-1)\ln t}}}</math> | :<math>{\displaystyle \Pi (x)=\mathrm {Li} (x)-\sum _{\rho }\mathrm {Li} (x^{\rho })-\ln 2+\int \limits _{x}^{\infty }{\frac {\mathrm {d} t}{t(t^{2}-1)\ln t}}}</math> | ||
| Zeile 173: | Zeile 173: | ||
* Aus der Riemannschen Vermutung folgt eine sehr scharfe Restgliedabschätzung im Primzahlsatz der Form <math>\pi(x) = \mathrm{Li}\,x+\mathcal{O}(\sqrt x\cdot\log x)</math>. <!-- Als eine Folge davon ließen sich schnelle Primzahltests entwickeln, welche wiederum essentiell in der modernen Kryptographie sind. (RSA – Verfahren…?) --> | * Aus der Riemannschen Vermutung folgt eine sehr scharfe Restgliedabschätzung im Primzahlsatz der Form <math>\pi(x) = \mathrm{Li}\,x+\mathcal{O}(\sqrt x\cdot\log x)</math>. <!-- Als eine Folge davon ließen sich schnelle Primzahltests entwickeln, welche wiederum essentiell in der modernen Kryptographie sind. (RSA – Verfahren…?) --> | ||
| − | * Unter Annahme der allgemeinen Riemannschen Hypothese wurde 1975 von Gary L. Miller der | + | * Unter Annahme der allgemeinen Riemannschen Hypothese wurde 1975 von Gary L. Miller der [[Der_kleine_Satz_von_Fermat#Der_Miller-Rabin_Test|Miller-Rabin Test]] vorgestellt. Dieser war der erste Primzahltest mit polynomieller Laufzeit. 2002 stellten Agrawal, Kayal, und Saxena den AKS-Primzahltest vor, welcher auch in polynomieller Zeit läuft und nicht von der Korrektheit der Riemannschen Hypothese abhängt. |
* In den 1970er Jahren entdeckte Hugh Montgomery, dass die Verteilung der Abstände aufeinanderfolgender Nullstellen eine ähnliche Verteilung wie die Eigenwerte hermitescher Zufallsmatrizen (vgl. dazu auch den Artikel [[Zufallsmatrizen - Bohemians und die geheimnisvolle Ordnung im Chaos]]) zeigt. Insgesamt scheint es also, dass tiefe Verbindungen zwischen der Riemannschen Vermutung und zahlreichen anderen Gebieten der Mathematik und Physik existieren müssen, was auch viele verschiedene Beweisideen der letzten Jahrzehnte zeigen. | * In den 1970er Jahren entdeckte Hugh Montgomery, dass die Verteilung der Abstände aufeinanderfolgender Nullstellen eine ähnliche Verteilung wie die Eigenwerte hermitescher Zufallsmatrizen (vgl. dazu auch den Artikel [[Zufallsmatrizen - Bohemians und die geheimnisvolle Ordnung im Chaos]]) zeigt. Insgesamt scheint es also, dass tiefe Verbindungen zwischen der Riemannschen Vermutung und zahlreichen anderen Gebieten der Mathematik und Physik existieren müssen, was auch viele verschiedene Beweisideen der letzten Jahrzehnte zeigen. | ||
| Zeile 218: | Zeile 218: | ||
* https://de.wikipedia.org/wiki/Miller-Rabin-Test | * https://de.wikipedia.org/wiki/Miller-Rabin-Test | ||
* https://de.wikipedia.org/wiki/AKS-Primzahltest | * https://de.wikipedia.org/wiki/AKS-Primzahltest | ||
| + | |||
| + | == Autoren == | ||
| + | * Fiona Teßmann | ||
| + | * Moritz Barth | ||
| + | * Finn Prem | ||
| + | * Tobias Thaller | ||
Aktuelle Version vom 17. April 2021, 19:29 Uhr
Die Riemannsche Vermutung oder Riemannsche Hypothese besagt, dass alle nicht-trivialen Nullstellen der Riemannschen Zeta-Funktion einen Realteil von genau [math]\frac{1}{2}[/math] haben. Sie wurde 1859 von Bernhard Riemann in seiner Arbeit Über die Anzahl der Primzahlen unter einer gegebenen Größe formuliert und gilt als ein bedeutendes ungelöstes Problem der Mathematik. Sie ist von besonderem Interesse für die Zahlentheorie, da sie eng mit der statistischen Verteilung der Primzahlen zusammenhängt.
Die Riemannsche Vermutung wurde im Jahr 1900 von David Hilbert auf seine Liste 23 wichtiger Jahrhundertprobleme gesetzt und im Jahr 2000 vom Clay Mathematics Institute in die Liste der sieben Millennium-Probleme der Mathematik aufgenommen.
Einführung
Die Untersuchung der Primzahlen steht im Zentrum der Zahlentheorie, jedoch scheint ein detailliertes Verständnis ihrer unerreichbar fern. Um mehr über sie zu erfahren, ist es daher sinnvoll, stattdessen ihre statistische Verteilung zu untersuchen. Dabei stellt sich unter anderem die Frage, wie viele Primzahlen unter einer gegebenen natürlichen Zahl existieren. Diese Frage kann in der Sprache der Mathematik mit Hilfe der Primzahlfunktion
- [math]\displaystyle{\pi (x):=\left|\{{p\leq x\ \mid p ~\text{prim}}\}\right|}[/math]
dargestellt werden.
Riemann gelang es nun 1859 für diese Funktion einen analytischen Ausdruck zu finden. Dieser Ausdruck beschreibt die Primzahlen exakt und enthält alle ihre Informationen. Da jedoch mit diesem das Bestimmen von Primzahlen mit sehr viel Aufwand verbunden ist und sich numerische Methoden dafür besser eignen, gilt damit das Primzahlproblem nicht als gelöst. Der Ausdruck ist jedoch von theoretischem Interesse, da mit ihm sehr genaue Abschätzungen über die Verteilung der Primzahlen gemacht werden können.
In Riemanns analytischem Ausdruck für [math]\pi (x)[/math] taucht eine Summe über die Nullstellen [math]{\rho }[/math] der Riemannschen Zeta-Funktion [math] \zeta (s) [/math] auf. Diese besitzt so genannte "triviale" Nullstellen, welche bei den negativen geraden Zahlen liegen. Diese folgen also einem einfachen Muster und sind damit bekannt. Es gibt jedoch noch unendlich viele weitere Nullstellen der Zeta-Funktion welche "nicht-triviale" Nullstellen genannt werden. Die Riemannsche Hypothese betrachtet genau diese Nullstellen und besagt:
Der Realteil aller nicht-trivialen Nullstellen der Riemannschen Zeta-Funktion beträgt [math]\frac{1}{2}[/math].
Viele prominente Mathematiker haben sich seit ihrer Formulierung mit der Riemannschen Vermutung auseinander gesetzt. Sie ist jedoch bis jetzt unbewiesen. Durch umfassenden Einsatz von Computern ist es gelungen, die Riemannsche Vermutung für die ersten 10 Billionen Nullstellen der Zeta-Funktion zu verifizieren. Da es jedoch unendlich viele Nullstellen gibt, könnte sie auf diese Weise nur durch Angabe eines expliziten Gegenbeispiels widerlegt, jedoch nicht bewiesen werden.
Riemannsche Zeta-Funktion
Dirichlet-Reihen
Die Riemannsche Zeta-Funktion [math] \zeta (s) [/math] ist eine komplexwertige Funktion. Häufig wird sie für [math]\text{Re}(s) \gt 1[/math] über eine Dirichlet-Reihe definiert, nämlich
- [math]\displaystyle \zeta (s) = \sum_{n=1}^\infty \frac{1}{n^s} [/math]
Eine Dirichlet-Reihe ist allgemein definiert als
- [math]\displaystyle F(s) = \sum_{n=1}^\infty \frac{f(n)}{n^s}[/math]
mit [math]s \in \mathbb{C}[/math], die Zeta-Funktion entspricht also der Dirichlet-Reihe mit [math]f(n) = 1[/math].
[math] \zeta (1)[/math] entspricht hierbei der bekannten harmonischen Reihe, darum ist es wenig verwunderlich, dass die Dirichlet-Reihe bei [math]\text{Re}(s) \gt 1 [/math] konvergiert, während dies für [math] \text{Re}(s) \leq 1 [/math] nicht der Fall ist. Deshalb charakterisiert die Dirichlet-Reihe die Zeta-Funktion nur für [math]\text{Re}(s) \gt 1 [/math]. Die Berechnung des Wertes [math]\zeta (2) [/math] ist als das Basler Problem bekannt.
Euler-Produkt
Das Euler-Produkt einer Dirichlet-Reihe [math] F(s) [/math] ist allgemein definiert als
- [math]\displaystyle F(s) = \prod _{p ~\text{prim}} \sum_{k = 0}^\infty \frac{f(p^k)}{p^{ks}} [/math].
Im Fall [math] f(s) = 1 [/math] ist dies gleich der Zeta-Funktion, und es gilt
- [math]\displaystyle \zeta (s) = \prod _{p ~\text{prim}} \sum_{k = 0}^\infty \frac{1}{p^{ks}}~~~[/math] für [math]\text{Re}(s) \gt 1 [/math].
Da jede Summe eine geometrische Reihe mit Quotient [math] p^{-s} [/math] bildet, folgt
- [math]\displaystyle \zeta (s) = \prod _{p \text{ prim}} \frac{1}{1- \frac{1}{p^s}}~~~ [/math] für [math]s \in \mathbb{C}, \text{Re}(s) \gt 1 [/math].
Ein schöner Beweis der Gleichheit dieser Darstellung mittels Siebtechnik ist hier zu finden.
Analytische Fortsetzung
Eine komplexe Funktion, die an jedem Punkt einer zusammenhängenden offenen Menge [math]U[/math] komplex differenzierbar ist, heißt holomorph in [math]U[/math]. Ist eine holomorphe Funktion [math]f[/math] nur auf einer Teilmenge einer Obermenge definiert, so existiert höchstens eine Funktion [math]f^*[/math], welche auf der Teilmenge mit [math]f[/math] übereinstimmt und in der Obermenge holomorph ist. Diese nennt man die analytische Fortsetzung von [math]f[/math]. Die Riemannsche Zeta-Funktion lässt sich eindeutig auf ganz [math]\mathbb{C}[/math] fortsetzen, mit einer Definitionslücke bei [math]s = 1[/math].
Um die erweiterte Form einmal gesehen zu haben, findet sich hier eine Darstellung mit der Gamma Funktion [math]\Gamma [/math] und den Bernoullizahlen [math]B_n[/math], für welche wir auf entsprechende Wikipedia Artikel verweisen wollen:
- [math]\displaystyle \zeta (s) = \frac{1}{\Gamma (s)} \left( \frac{1}{s-1} \frac{1}{2s} \sum_{n=2}^\infty \frac{B_n}{n!} \frac{1}{s + n -1} + \int_1 ^\infty \frac{x^{s-1}}{e^x-1} \right) ~~~ [/math] für [math]s \in \mathbb{C} \backslash \{ 1\} [/math]
Eine Herleitung und weiterführende Informationen sind aber zum Beispiel hier gegeben und eine graphische Anschauung in diesem Video.
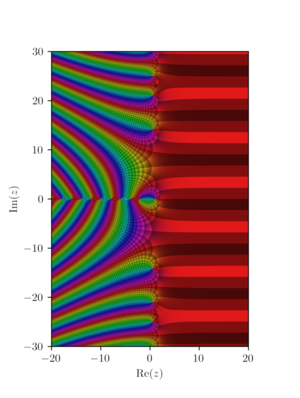
Nullstellen der Zeta-Funktion
Von besonderem Interesse sind die Nullstellen der Zeta-Funktion. Die sogenannten trivialen Nullstellen liegen auf -2, -4, -6 usw. Diese ergeben sich, da die Gamma-Funktion bei allen negativen ganzen Zahlen Polstellen hat, wobei [math]\frac{1}{\Gamma (s)}[/math] dort eine Nullstelle hat, für ungerade Werte werden diese jedoch durch Polstellen des Klammemerausdrucks "weggehoben". Die Position der Nullstellen des Klammerausdrucks (den nicht-trivialen Nullstellen) zu bestimmen, ist eines der größten ungelösten Probleme der Mathematik. Die Riemannsche Vermutung besagt, dass alle nicht-trivialen Nullstellen den Realteil [math]\frac{1}{2}[/math] haben, was bisher weder bestätigt noch widerlegt werden konnte.
Zusammenhang mit Primzahlen
Primzahlsatz
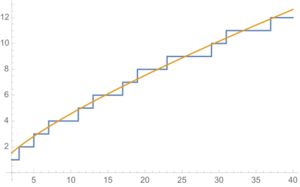
Um den Verlauf der bereits erwähnten Primzahlfunktion [math] \pi (x) [/math] abzuschätzen, eignet sich der Primzahlsatz, der dafür eine konkrete Näherungsfunktion angibt:
- [math]\displaystyle \lim _{{x\to \infty }}{\frac {\pi (x)}{{\frac {x}{\ln(x)}}}}=1~~[/math], also [math]\displaystyle \pi (x) \sim \frac{x}{\ln {x}} [/math]
- ([math]\sim[/math] bedeutet "asymptotisch äquivalent", d.h. die Abschätzung wird prozentual immer genauer)
Hans von Mangoldt konnte 1895 beweisen, dass der Primzahlsatz dazu äquivalent ist, dass die Riemannsche Zeta-Funktion keine Nullstellen mit Realteil 1 hat.
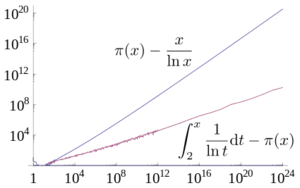
Eine bessere Approximation als [math]\displaystyle \frac{x}{\ln {x}} [/math] gibt der Integrallogarithmus [math]\displaystyle \mathrm{Li}(x):=\int _{2}^{x}{\frac { \mathrm{d}t }{\ln {t}} } [/math]
Verbesserung der Vorhersage
Wäre eine analytische Funktionsgleichung der Primzahlfunktion bekannt, wäre die genaue Verteilung der Primzahlen bekannt, und ob eine Zahl eine Primzahl ist, könnte einfach abgelesen werden. Diese analytische Form zu finden, ist das Ziel der ganzen folgenden Gleichungen und Umformungen. Letztendlich wird eine konkrete Formel gefunden, in die aber alle (unendlich vielen) nicht-trivialen Nullstellen der Zeta-Funktion eingesetzt werden müssen.
Disclaimer: Die folgenden Schritte sollen ein prinzipielles Verständnis des Zusammenhangs mit der Primzahlfunktion ermöglichen; da sie dafür stark vereinfacht wurden, reichen die angegebenen Formeln und Methoden nicht aus, um jeden der Schritte nachvollziehen zu können.
Die Zeta-Funktion hängt über ihre Produktschreibweise direkt mit den Primzahlen zusammen:
- [math]\displaystyle \zeta (s)=\prod _{p\ {\text{prim}}}{\frac {1}{1-{\frac {1}{p^{s}}}}}~~~[/math]für [math]\text{Re}(s)\gt 1[/math]
Diese zweite Form der Zeta-Funktion lässt sich umwandeln in eine Formel für [math]\ln {\zeta(s)}[/math] :
- [math]{\displaystyle \ln \zeta (s)=\sum _{p\ \mathrm {prim} }\sum _{n=1}^{\infty }{\frac {p^{-ns}}{n}}}[/math]
Um [math] \ln \zeta (s) [/math] im nächsten Schritt in einer geschlossenen Form zu schreiben, wird [math] \Pi (x) [/math] eingeführt:
- [math]{\displaystyle \Pi (x)=\sum _{p^{n}\lt x}{\frac {1}{n}}}[/math]
Unter Verwendung dieser Funktion lässt sich [math]\ln {\zeta(s)}[/math] in Integralform bringen:
- [math]{\displaystyle \ln \zeta (s)=s\int \limits _{0}^{\infty }x^{-s-1}\Pi (x)\mathrm {d} x}[/math]
Dieser Ausdruck lässt sich über eine inverse Mellin-Transformation (siehe Wikipedia) "umkehren" zu:
- [math]{\displaystyle \Pi (x)={\frac {1}{2\pi i}}\int \limits _{c-i\infty }^{c+i\infty }{\frac {\ln \zeta (s)}{s}}x^{s}\mathrm {d} s}~~~[/math] mit einem [math] c\gt 1 [/math][math]~~~(*)[/math]
Eine weitere von Riemann eingeführte Funktion, die Riemannsche Xi-Funktion, benutzt in ihrer Produktdarstellung alle nicht-trivialen Nullstellen [math]\rho[/math] der Zeta-Funktion:
- [math]{\displaystyle \xi (s)={\frac {1}{2}}\prod _{\rho }\left(1-{\frac {s}{\rho }}\right)}[/math]
Hieraus lässt sich eine zweite, deutlich kompliziertere Form für [math]\ln {\zeta(s)}[/math] formulieren:
- [math]{\displaystyle \ln \zeta (s)=\sum _{\rho }\ln \left(1-{\frac {s}{\rho }}\right)-\ln 2-\ln \Gamma \left(1+{\frac {s}{2}}\right)+{\frac {s}{2}}\ln \pi -\ln(s-1)}[/math]
Indem man [math]\ln {\zeta(s)}[/math] in der Gleichung [math](*)[/math] durch obigen Ausdruck substituiert, erhält man (was nochmals einige Arbeit vonseiten Riemanns erforderte) letztendlich eine Formel für [math]\Pi (x)[/math], in der über alle nicht-trivialen Nullstellen [math] \rho [/math] der Zeta-Funktion summiert wird:
- [math]{\displaystyle \Pi (x)=\mathrm {Li} (x)-\sum _{\rho }\mathrm {Li} (x^{\rho })-\ln 2+\int \limits _{x}^{\infty }{\frac {\mathrm {d} t}{t(t^{2}-1)\ln t}}}[/math]
Über die Möbius-Inversion lässt sich folgender Zusammenhang zwischen [math]\pi (x)[/math] und [math]\Pi (x)[/math] herleiten, mit der Möbiusfunktion [math]\mu (n)[/math] (siehe Wikipedia) :
- [math] {\displaystyle {\pi (x)=\sum _{n=1}^{\infty }{\frac {\mu (n)}{n}}\Pi (x^{1/n})}} [/math]
Benutzt man hier nun für [math]\Pi (x)[/math] den Ausdruck mit den nicht-trivialen Nullstellen der Zeta-Funktion, hat man eine analytische Darstellung der Primzahlfunktion [math]\pi (x)[/math] hergeleitet, was das ursprüngliche Ziel war. Das Problem liegt ab hier also im Finden und in der Verteilung der nicht-trivialen Nullstellen der Zeta-Funktion. In diese Formel müssten unendlich viele Nullstellen eingesetzt werden, was praktisch nicht möglich ist. Man setzt daher nur eine bestimmte Zahl von Nullstellen ein und erhält so zumindest eine berechenbare Näherung für [math] \pi (x) [/math], die umso genauer ist, je mehr Nullstellen verwendet werden.
Bedeutung in der Wissenschaft
Es gibt sowohl eine Vielzahl von wichtigen Theoremen und Aussagen die aus der Riemannschen Vermutung folgen bzw. nur unter der Annahme, dass diese der Wahrheit entspricht, gezeigt werden konnten, als auch einige Aussagen für die gezeigt werden konnte, dass sie äquivalent zu dieser sind. Das bedeutet natürlich, dass einzig die Lösung des Riemannschen Problems Licht in viele verschiedene Bereiche der Mathematik und auch der Physik bringen würde. Dazu nun einige konkrete Beispiele, wie die Riemannsche Vermutung mit aktuellen Forschungsgebieten und Anwendungsfällen verknüpft ist:
- Aus der Riemannschen Vermutung folgt eine sehr scharfe Restgliedabschätzung im Primzahlsatz der Form [math]\pi(x) = \mathrm{Li}\,x+\mathcal{O}(\sqrt x\cdot\log x)[/math].
- Unter Annahme der allgemeinen Riemannschen Hypothese wurde 1975 von Gary L. Miller der Miller-Rabin Test vorgestellt. Dieser war der erste Primzahltest mit polynomieller Laufzeit. 2002 stellten Agrawal, Kayal, und Saxena den AKS-Primzahltest vor, welcher auch in polynomieller Zeit läuft und nicht von der Korrektheit der Riemannschen Hypothese abhängt.
- In den 1970er Jahren entdeckte Hugh Montgomery, dass die Verteilung der Abstände aufeinanderfolgender Nullstellen eine ähnliche Verteilung wie die Eigenwerte hermitescher Zufallsmatrizen (vgl. dazu auch den Artikel Zufallsmatrizen - Bohemians und die geheimnisvolle Ordnung im Chaos) zeigt. Insgesamt scheint es also, dass tiefe Verbindungen zwischen der Riemannschen Vermutung und zahlreichen anderen Gebieten der Mathematik und Physik existieren müssen, was auch viele verschiedene Beweisideen der letzten Jahrzehnte zeigen.
- Wird die Riemannsche Vermutung als korrekt vorausgesetzt, so kann gezeigt werden, dass sich die Anzahl der Primfaktoren einer Zahl statistisch zufällig verhält. Ob eine Zahl sich also in gerade oder ungerade viele Primfaktoren zerlegen lässt, entspricht dann also genau der Wahrscheinlichkeit, ob bei einem Münzwurf Kopf oder Zahl fällt. Dieses statistische Verhalten würde natürlich in der Zahlentheorie eine sehr große Bedeutung bekommen.
Insgesamt vermutet man, dass sich hinter der Riemannschen Vermutung eine fundamentale Theorie verbirgt, sodass die Lösung dieses Millennium-Problems einen sehr großen Fortschritt in der Mathematik (besonders im Verständnis der Zahlentheorie) mit sich bringen würde. Dies ist die Hauptmotivation vieler Mathematiker die auch heute noch (162 Jahre nach der erstmaligen Veröffentlichung der Riemannsche Vermutung) an rigorosen Beweisen arbeiten.
Argumente für und gegen die Korrektheit der Riemannschen Vermutung
Abschließend stellt sich nun natürlich die Frage, ob die Riemannsche Vermutung denn nun korrekt ist oder nicht.
Auf jeden Fall ist heutzutage die vorherrschende wissenschaftliche Ansicht, dass Bernhard Riemann mit seiner Vermutung recht hatte. Dies mag vor allem daran liegen, dass bereits die ersten 10 Billionen (10 000 000 000 000) nicht-trivialen Nullstellen durch Superrechner überprüft wurden und mit der Behauptung übereinstimmen, aber auch daran, dass es schon viele Theoreme gab, die zuerst nur mit der Annahme der Korrektheit der Riemannschen Vermutung gezeigt werden konnten, sich später jedoch auch unabhängig von dieser als korrekt herausstellten (die "Vorhersagen" mithilfe der Hypothese stimmten folglich, was für deren Korrektheit spricht). Ein Beispiel dafür wäre die schwache Goldbachsche Vermutung (siehe Wikipedia). Die Riemannsche Vermutung passt also sehr gut in die gegenwärtige mathematische Theorie, mehr noch, ein Widerlegen der Hypothese würde das jetzige Verständnis vieler noch nicht vollständig gelöster Probleme komplett durcheinanderbringen und zum Umdenken zwingen.
Dennoch kann ohne einen vollständigen Beweis natürlich nicht einfach davon ausgegangen werden, dass eine Annahme korrekt ist. Alleine, dass einige der renommiertesten Mathematiker die es je gab, wie z.B. Alan Turing, dachten, dass die Vermutung nicht stimmen würde, gibt einem zu denken; eines der ersten Dinge, die Turing mit seinem ersten Modell eines Computers berechnete, waren Nullstellen der Zeta-Funktion, um eine zu finden, die nicht mit der Behauptung übereinstimmt. Aber auch die Billionen von bereits verifizierten Nullstellen könnten einen nur in die Irre leiten. So tritt z.B. das erste Gegenbeispiel eines ähnlichen Theorems im Zusammenhang mit der Skewes-Zahl (siehe Wikipedia) erst in einer Größenordnung von 10316 auf. Mit anderen Worten kann es also sein, dass das eigentlich charakteristische Verhalten der Zeta-Funktion erst bei unerreichbar großen Werten eintritt, wodurch die ersten 10 Billionen Nullstellen entscheidend an Wichtigkeit verlieren würden.
Abschließend kann man sagen, dass es einige spezielle Eigenschaften der Zeta-Funktion gibt, die mal für und mal gegen die Riemannsche Vermutung sprechen. Insgesamt kann jedoch nach momentanem Wissensstand davon ausgegangen werden, dass die Riemannsche Vermutung korrekt ist, man sollte jedoch immer im Hinterkopf behalten, dass sie bis jetzt noch nicht vollständig gezeigt werden konnte. Trotz der bereits vielfältigen Benutzung der Vermutung in zahlreichen Forschungsarbeiten wäre ein vollständiger Beweis ein sehr großer Schritt für die Mathematik und würde viel zu einem tieferen Verständnis zahlreicher mathematischer und physikalischer Bereiche beitragen. Jetzt wisst ihr also, was ihr tun könnt, um berühmt zu werden und die ganze Welt voranzubringen. Achtet dann darauf, dass euer Beweis auch nicht widerlegt werden kann, im Gegensatz zu den hunderten veröffentlichten Beweisversuchen vor euch! Viel Erfolg!
Quellen
- https://de.wikipedia.org/wiki/Bernoulli-Zahl
- https://de.wikipedia.org/wiki/Primzahlsatz
- https://dmg.tuwien.ac.at/drmota/Sas_primetests_endversion.pdf
- https://de.wikipedia.org/wiki/Miller-Rabin-Test
- https://de.wikipedia.org/wiki/AKS-Primzahltest
Autoren
- Fiona Teßmann
- Moritz Barth
- Finn Prem
- Tobias Thaller