Arctic Circle Theorem: Unterschied zwischen den Versionen
| (114 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | In diesem Artikel wollen wir | + | In diesem Artikel wollen wir das "Arctic Circle"-Theorem beschreiben, welches eine mathematische Spielerei beschreibt, die mit Schachbrettern und Dominosteinen zu tun hat. Wir beginnen damit die Überdeckungen von Schachbrettern mit Dominosteinen zu untersuchen. Danach betrachten wir eine spezielle Form von abgeschnittenen Schachbrettern, den Aztekendiamanten, die uns zum Arctic Circle Theorem führen werden. |
| − | === Schachbretter und Dominosteine === | + | == Grundlagen über Schachbretter und Dominosteine == |
| + | ===Schachbretter und Dominosteine=== | ||
[[Datei:Schachbrettbelegung.gif|mini|Normales und Brett mit abgeschnittenen Ecken werden mit Dominosteinen belegt]] | [[Datei:Schachbrettbelegung.gif|mini|Normales und Brett mit abgeschnittenen Ecken werden mit Dominosteinen belegt]] | ||
| − | Ein typisches Schachbrett besteht aus einem Brett mit 8 x 8 Feldern. Diese sind abwechselnd Schwarz und Weiß. | + | Ein typisches Schachbrett besteht aus einem Brett mit 8 x 8 Feldern. Diese sind abwechselnd Schwarz und Weiß. Wir stellen uns nun die Frage wie viele 2x1 Dominosteine benötigt werden um ein Schachbrett komplett abzudecken. Offensichtlich gibt es hierbei mehr als eine Möglichkeit das Schachbrett mit Dominosteinen abzudecken, wir sprechen nun immer von einer Überdeckung wenn wir eine solche Möglichkeit meinen. Während wir im Folgenden immer 2x1 Dominosteine betrachen werden, so werden wir die größe und Form der Schachbretter variieren. Wir sprechen dann weiterhin vom (Schach)-Brett. Wir wollen nun die Frage nach der Anzahl der Überdeckungen etwas nach hinten verschieben und uns erst einmal überlegen, wann beliebige Schachbretter überhaupt eine Überdeckung besitzen. |
| − | |||
| − | + | === Abgeschnittene Schachbretter === | |
| − | + | Auf ein normales Schachbrett mit 8 x 8 Feldern passen genau 32 Dominosteine. Was passiert, wenn man nun beliebig Felder aus diesem Schachbrett entfernt? Hier fällt auch schon die erste Bedingung auf, wir benötigen immer eine gerade Anzahl an Feldern für die Überdeckung mit Dominosteinen. Zu erst wollen wir uns den einfachen Fall ansehen, bei dem die diagonal zueinander liegenden Ecken entfernt werden. Wir haben nun also 62 Felder, die wir mit 31 Dominosteinen abdecken wollen. Nun kann man versuchen das verkleinerte Schachbrett zu überdecken. Das muss allerdings unweigerlich scheitern, denn wir haben zwei Felder der gleichen Farbe entfernt. Dominosteine liegen allerdings immer auf einem schwarzen und einem weißen Feld. Dadurch bleiben bei jedem Versuch zwei Felder der gleichen Farbe übrig. Das heißt bei abgeschnittenen Schachbrettern muss immer die gleiche Anzahl an weißen und schwarzen Feldern enthalten sein um ein überdeckbares Schachbrett zu erhalten. | |
| − | + | ||
| − | + | === Die Kasteleyn-Fisher-Temperley-Formel === | |
| − | + | ||
| − | + | Diese Formel wurde 1961 entwickelt und beschreibt die Anzahl <math>B(m,n)</math> der möglichen Belegungen eines rechteckigen <math>m \times\ n</math> - Schachbrettes. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | === | + | <math>B(m,n) = \prod_{j=1}^{\lceil \frac{m}{2}\rceil}\prod_{k=1}^{\lceil \frac{n}{2}\rceil}\left(4\cos^2{\frac{j\pi}{m+1}}+4\cos^2{\frac{k\pi}{n+1}}\right)</math> |
| − | |||
| − | |||
| − | |||
| − | ( | ||
| − | + | Beispiel der Anwendung dieser Formel anhand eines <math> 2 \times 4</math>- Schachbretts: | |
| − | + | <math>B(2,4)=\ \prod_{j=1}^\frac{2}{2}\prod_{k=1}^\frac{4}{2}\left(4\cos^2{\frac{j\pi}{2+1}}+4\cos^2{\frac{k\pi}{4+1}}\right)=\ \prod_{j=1}^{1}\prod_{k=1}^{2}\left(4\cos^2{\frac{j\pi}{3}}+4\cos^2{\frac{k\pi}{5}}\right)</math> | |
| − | + | Nach Auflösen der Produkte ergibt sich: | |
| − | + | <math>B(2,4)=\left(4{cos}^2{\frac{1\pi}{3}}+4{cos}^2{\frac{1\pi}{5}}\right)\left(4{cos}^2{\frac{1\pi}{3}}+4{cos}^2{\frac{2\pi}{5}}\right) = {5}</math> | |
| + | Somit gibt es in diesem Beispiel 5 mögliche Belegungen des Schachbretts. Für das gewöhnliche <math> 8 \times 8</math>-Schachbrett erhalten wir für die Anzahl an möglichen Überdeckungen: <math> 12.988.816</math> | ||
| − | + | Wenn m und n ungerade Zahlen sind, so hat auch das Schachbrett eine ungerade Anzahl an Feldern und kann deshalb nicht gekachelt werden. Die Formel ergibt für diesen Fall immer den Wert 0. | |
| − | + | Nun wird die Funktionsweise dieser Formel anhand eines Prinzips verdeutlicht, welches nicht nur für rechteckige Schachbretter, sondern allgemein gültig ist. Hier muss lediglich die Anzahl der schwarzen und weißen Felder identisch sein und kein Loch enthalten sein. | |
| + | [[Datei:1.png|mini|Bestimmung der möglichen Belegungen|alternativtext=]] | ||
| + | In der Abbildung rechts ist als Beispiel ein zufälliges und nicht rechteckiges Schachbrett dargestellt. Zunächst werden jeweils die schwarzen und weißen Felder durchgezählt. Die Positionierung der Zahlen spielt hierbei keine Rolle. | ||
| + | Anschließend werden alle direkt aneinander liegenden Zahlen in der nebenstehenden Tabelle markiert. Diagonal zueinander befindliche Felder sind hierbei ausgeschlossen. Alle in Verbindung stehenden Zahlen werden mit einer 1 markiert. Sind die beiden Zahlen identisch, so werden sie in der Tabelle mit der imaginären Zahl i versehen. Die restlichen Einträge der Tabelle werden auf Null gesetzt. | ||
| − | + | Die entstandene Tabelle kann nun direkt in eine Matrix übernommen werden, aus deren Determinante man die Anzahl der möglichen Belegungen des Schachbrettes ablesen kann. | |
| − | |||
| − | <math>\left( | + | [[Datei:2.1.png|mini|Mögliche Belegungen|alternativtext=]] |
| + | <math>\det K = \det \left(\begin{matrix}i&1&0&0&0\\1&i&1&0&0\\0&1&i&1&1\\0&0&0&i&1\\0&0&0&0&i\\\end{matrix}\right) = {3i}</math> | ||
| − | |||
| + | Das Vorzeichen und die imaginäre Zahl i sind bei den jeweiligen Ergebnissen zu vernachlässigen. Somit beträgt die Anzahl der möglichen Belegungen in unserem Beispiel 3. | ||
| + | Die unterschiedlichen Möglichkeiten für dieses Beispiel werden in nebenstehender Abbildung dargestellt. Wir wollen nun eine kurze Erklärung geben wie dieser Trick funktioniert. Wir erinnern uns an die bekannte Leibnitz-Formel für die Determinante: | ||
| − | + | <math>\det K = \sum_{\sigma \in S_5} sgn(\sigma) \prod_{i = 1}^{n} K_{i, \sigma(i)} </math> | |
| − | ( | + | Man kann sich jetzt überlegen, dass jede Permutation <math> \sigma</math> versucht ein schwarzes mit einem weißen Feld zu vereinigen. Ist dies für alle Felder möglich erhalten wir einen Summanden der ungleich Null ist. Es kann nun gezeigt werden, dass diese Summanden alle von der gleichen Art sind, also alle <math> 1</math>, <math> -1</math> oder <math> i</math>. Somit zählt die Determinante, wie viele der Permutationen möglich sind und der Betrag der Determinante gibt die Anzahl wieder. Der Zusammenhang mit der Kasteleyn-Fischer-Temperly-Formel besteht nun darin, dass es sich bei dem Matrix-Trick um eine Verallgemeinerung handelt. Es kann gezeigt werden, dass für reckeckige Schachbretter die Terme in der Formel gerade die Eigenwerte der Matrix <math> \left(\begin{matrix} 0 & K\\ K' & 0 \\\end{matrix} \right)</math> sind. |
| − | <math>\ | + | Berechnet man die mögliche Anzahl an Belegungen der <math>2\times n</math>-Schachbretter in aufsteigender Reihenfolge, so erhält man die [[Fibonacci Folge]]. |
| − | + | == Aztekendiamanten == | |
| − | + | === Definition der Aztekendiamanten === | |
| + | [[Datei:Aztekenfeld.gif|mini|Aztekenfelder verschiedener Größe]] | ||
| + | Wir betrachten beim Arctic Circle Theorem oder dem Aztek Diamond nun Schachbretter, bei denen nicht nur 2 Felder entfernt wurden, sondern im allgemeinen <math>n((n/2)-1)</math> Felder an allen vier Ecken entfernt wurden, sodass eine Raute in Pixelgraphik entsteht. | ||
| + | Somit hat das Feld nur noch <math>n((n/2)+1)</math> Feldern. | ||
| + | Dabei ist die Feldgröße angegeben in der maximalen Kästchenweite der Diagonale. | ||
| − | <math></math> | + | Die Felder haben dann folgendes Aussehen: |
| + | * Feldgröße 2 x 2 besteht aus 2 schwarzen 2 weißen Feldern | ||
| + | * Feldgröße 4 x 4 besteht aus 6 schwarzen 6 weißen Feldern | ||
| + | * Feldgröße 6 x 6 besteht aus 12 schwarzen 12 weißen Feldern | ||
| + | * Feldgröße 8 x 8 besteht aus 20 schwarzen 20 weißen Feldern | ||
| + | * ... | ||
| + | * Feldgröße <math>n \times n </math> für <math>n \geq 2 </math> besteht aus <math>n((n/2)+1)/2</math> schwarzen und <math>n((n/2)+1)/2</math> weißen Feldern. | ||
| + | Auch hier bestehen die Felder aus jeweils gleichvielen verschiedenfarbigen Feldern, da sonst die Überdeckung mit Dominosteinen nicht möglich ist, wie oben Bewiesen. | ||
| + | n ist hier immer gerade, da bei den Feldern die mit 2 begonnen wird und an allen Seiten neue Kästchen hinzugelegt wird. Also nach der Form Feldgröße = 2n mit <math>n \in \mathbb{N}</math>. | ||
| − | == | + | == Das Arctic Circle Theorem == |
| − | In der kombinatorischen Mathematik bestehen | + | In der kombinatorischen Mathematik bestehen Aztekendiamanten der Kardinalität (Ordnung) n aus allen Quadraten, deren Zentrum (x,y), die Gleichung <math>|x|+|y|<=n</math> erfüllen. Wir bezeichnen den n-ten Aztekendiamant mit <math>A(n)</math>. Die Anzahl wie oft man ein Aztec-Diamond der Ordnung <math>n</math> legen kann ist <math>2^{\frac{n(n+1)}{2}}</math>. Das Arctic Circle Theorem sagt nun, dass wenn n größer wird und damit die Anzahl der möglichen Überdeckungen größer wird, die Wahrscheinlichkeit, dass die Ecken des Diamanten jeweils in einer Farbe sind und sich in der Mitte eine kreisförmige chaotische Region befindet gegen 1 geht. Das heißt es gibt nur noch vernachlässigbar wenige Überdeckungen gibt die eine andere Struktur besitzen. Desweiteren kann für den Grenzfall [math]n \rightarrow \infty[/math] gezeigt werden, dass sich die chaotische Mitte im Mittel einem perfekten Kreis annähert. Jedes Domino wird genau ein schwarzes und ein weißes Feld treffen. Die Farben werden dann so festgelegt, je nachdem ob rechts, links oder oben, unten weiß oder schwarz ist. |
| + | [[Datei:Square dance gif mit 5sec.gif|alternativtext=|mini|Square Dance]] | ||
| − | + | === Tanzende Dominosteine === | |
| − | + | Um einen zufällig gefärbten Aztekendiamanten zu erhalten gibt es verschiedene Methoden. Einfach ein gegebenes Schachbrett zu färben ist leider keine praktikable Möglichkeit, da die Wahrscheinlichkeiten für jedes Feld und im Allgemeinen auch für jede Fabe unterschiedlich sind und nicht 25% betragen. Eine Möglichkeit wäre es jedoch zum Beispiel viele Diamanten in der gewünschten Größe zu erstellen und jeden dieser Diamanten mit einer möglichen Kombination an Dominosteinenen bedecken, sodass alle möglichen Kombinationen einmal vorkommen. Aus dieser Menge könnte dann ein zufälliger Aztekendiamant gezogen werden. Das Problem ist, dass auch diese Methode sehr (rechen-)aufwendig ist. | |
| − | Eine bessere Methode ist die sogenannte Square-Dance-Methode. Hierbei werden ausgehend vom einfachsten Diamanten | + | Eine bessere Methode ist die sogenannte Square-Dance-Methode. Hierbei werden ausgehend vom einfachsten Diamanten <math> A(1)</math>, ( ein <math> 2 \times 2</math> Quadrat) schrittweise beliebig große Aztenkendiamanten aufgebaut. Hierbei wird jeweils eine Farbe mit einer Richtung assoziiert, im Beispiel rechts entspricht blau nach oben. |
| − | Square-Dance-Algorithmus: | + | Der Square-Dance-Algorithmus lautet: |
| − | # | + | # <math> 2 \times 2</math> Diamant zufällig mit zwei Dominosteinen belegen. |
| − | # Den Diamant um eine Ordung erweitern | + | # Den Diamant um eine Ordung erweitern. |
# Prüfen ob zwei Felder aufeinander zeigen, da hier kein Verschieben möglich wäre, diese Felder entfernen. | # Prüfen ob zwei Felder aufeinander zeigen, da hier kein Verschieben möglich wäre, diese Felder entfernen. | ||
| − | # Die Dominosteine in die | + | # Die Dominosteine in die zu den Farben gehörigen Richungen verschieben. |
| − | # Die resultierenden | + | # Die resultierenden <math> 2 \times 2</math> Felder zufällig belegen. |
# zurück zu Schritt 2 gehen. | # zurück zu Schritt 2 gehen. | ||
Anhand dieses Vorgehens ist es recht einfach zu sehen wie der Arctic Circle und vor allem die stabilen Ecken entstehen. | Anhand dieses Vorgehens ist es recht einfach zu sehen wie der Arctic Circle und vor allem die stabilen Ecken entstehen. | ||
| + | [[Datei:Eis 2 cases new.png|mini|Fall 1. links und Fall 2. rechts]] | ||
| − | + | === Arktischer Kreis und stabile Ecken === | |
| − | + | Anhand obigen Vorgehens ist es recht einfach zu sehen, aber doch sehr erstaunlich, wie trotz des von Anfang an zufälligen Vorgehens, ein Aztekendiamant mit einigen sehr stabilen und geordeneten Regionen entsteht. Das erste Merkmal ist schon nach nur wenigen Iterationen sichtbar, nämlich die stabilen Ecken. Diese Struktur entsteht, da eine Ecke, z.B. oben, entweder: | |
| − | |||
# mit zwei Dominosteinen, die nach rechts und links zeigen ausgefüllt ist, oder | # mit zwei Dominosteinen, die nach rechts und links zeigen ausgefüllt ist, oder | ||
# mit einem nach oben zeigendem Stein. | # mit einem nach oben zeigendem Stein. | ||
| − | Im ersten Fall, entseht im nächsten Iterationsschritt in der oberen Ecke ein freies | + | Im ersten Fall, entseht im nächsten Iterationsschritt in der oberen Ecke ein freies <math> 2 \times 2</math> Feld, was wieder entweder mit 1. oder 2. gefüllt wird. Im zweiten Fall jedoch verschiebt sich der blaue Stein jedoch nach oben und sitzt wieder in der oberen Ecke. Da für den ersten Fall im nächsten Schritt die Wahrscheinlichkeiten für beide Fälle 50/50 sind, wird irgendwann Fall 2. eintreten. Dieser Stein blockiert dann dauerhaft die obere Ecke. Das selbe Prinzip sorgt dafür, dass unterhalb dieser Spitze sich nach und nach ein immer größer werdendes Feld an gleichen Steinen ansammelt. Dies gilt natürlich für alle Ecken, sodass das charateristisches "Eis" in den Ecken entsteht. |
| − | + | [[Datei:FY1GU gedreht.png|mini|Ein großer Aztekendiamant mit erkennbarem arktischem Kreis und stabilen Ecken]] | |
| − | Diese stabile Verschieben in die Ecken sorgt außerdem für einen weiteren Effekt, nämlich dass in der Mitte des Diamanten ein Kreis von ungeordneten Dominosteinen entsteht. Dies ist der Arktische Kreis, der Namensgeber des Arctic Circle Theorem. | + | Diese stabile Verschieben in die Ecken sorgt außerdem für einen weiteren Effekt, nämlich dass in der Mitte des Diamanten ein Kreis von ungeordneten Dominosteinen entsteht. Dies ist der Arktische Kreis, der Namensgeber des Arctic Circle Theorem. Das Arctic Circle Theorem besagt weiter, dass die zentrale Region für steigendes n sich einem Kreis annähert. Dieser hat den Radius <math> \frac{n}{\sqrt{2}}</math>. |
| + | * | ||
| − | // | + | === Anzahl der Überdeckungen === |
| + | Nachdem wir nun den Tanz der Dominosteine verstanden haben, wollen wir nun die Anzahl der Überdeckungen für einen beliebigen Aztekendiamant <math> A(n)</math> berechnen. Wir beginnen mit <math> A(1)</math> und sehen ein, dass es für diesen genau zwei Überdeckungen gibt. Ausgehend von einer dieser Möglichkeiten schieben wir nun im erweiterten <math> A(2)</math> die Dominosteine in die durch den Pfeil angezeigte Richtung. Es bleiben nun zwei 4x4 Felder frei, die auf <math> 2^2</math> Weisen überdeckt werden können. Dies ist das zentrale Argument im rigorosen Beweis der Aussage. Es kann nämlich analog zu unseren Überlegungen gezeigt werden, dass im k-ten Schritt <math> 2^{k}</math> Möglichkeiten hinzukommen. Insgesamt erhalten wir also für den <math> A(n)</math> genau <math> 2^{1} \cdot 2^{2} \cdot ... \cdot 2^{n} = 2^{1 + 2 + 3 + ... + n} = 2^{\frac{n(n+1)}{2}}</math> mögliche Überdeckungen. | ||
<math> </math> | <math> </math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | == Quellen == | |
| − | |||
*Sciencia, Librero, ISBN: 978-90-8998-430-2, Seite 14f. | *Sciencia, Librero, ISBN: 978-90-8998-430-2, Seite 14f. | ||
*Fermats letzter Satz, Simon Singh, dtv, ISBN: 978-3-423-33052-7, Seite 44-50 | *Fermats letzter Satz, Simon Singh, dtv, ISBN: 978-3-423-33052-7, Seite 44-50 | ||
| + | *Dimers and Dominoes, James Propp, arXiv:1405.2615 | ||
| − | Weiterführende Literatur | + | ==Weiterführende Literatur== |
*https://link.springer.com/article/10.1023/A:1008605912200 | *https://link.springer.com/article/10.1023/A:1008605912200 | ||
*https://archive.org/details/arxiv-math9801068/mode/2up | *https://archive.org/details/arxiv-math9801068/mode/2up | ||
| + | *http://www.issmys.eu/scientific-information/lectures-notes/the-arctic-circle-by-vincent-beffara | ||
| + | *https://www.youtube.com/watch?v=Yy7Q8IWNfHM | ||
| − | == | + | ==Autoren== |
| − | + | * | |
| − | + | * | |
| − | + | * | |
| − | + | *Alexander Fichtelmann | |
| − | + | *Julian Groth | |
| − | + | *Steven Göbl | |
| − | + | *Alicia Trabold | |
| − | |||
| − | |||
| − | |||
Aktuelle Version vom 16. April 2021, 14:05 Uhr
In diesem Artikel wollen wir das "Arctic Circle"-Theorem beschreiben, welches eine mathematische Spielerei beschreibt, die mit Schachbrettern und Dominosteinen zu tun hat. Wir beginnen damit die Überdeckungen von Schachbrettern mit Dominosteinen zu untersuchen. Danach betrachten wir eine spezielle Form von abgeschnittenen Schachbrettern, den Aztekendiamanten, die uns zum Arctic Circle Theorem führen werden.
Grundlagen über Schachbretter und Dominosteine
Schachbretter und Dominosteine
Ein typisches Schachbrett besteht aus einem Brett mit 8 x 8 Feldern. Diese sind abwechselnd Schwarz und Weiß. Wir stellen uns nun die Frage wie viele 2x1 Dominosteine benötigt werden um ein Schachbrett komplett abzudecken. Offensichtlich gibt es hierbei mehr als eine Möglichkeit das Schachbrett mit Dominosteinen abzudecken, wir sprechen nun immer von einer Überdeckung wenn wir eine solche Möglichkeit meinen. Während wir im Folgenden immer 2x1 Dominosteine betrachen werden, so werden wir die größe und Form der Schachbretter variieren. Wir sprechen dann weiterhin vom (Schach)-Brett. Wir wollen nun die Frage nach der Anzahl der Überdeckungen etwas nach hinten verschieben und uns erst einmal überlegen, wann beliebige Schachbretter überhaupt eine Überdeckung besitzen.
Abgeschnittene Schachbretter
Auf ein normales Schachbrett mit 8 x 8 Feldern passen genau 32 Dominosteine. Was passiert, wenn man nun beliebig Felder aus diesem Schachbrett entfernt? Hier fällt auch schon die erste Bedingung auf, wir benötigen immer eine gerade Anzahl an Feldern für die Überdeckung mit Dominosteinen. Zu erst wollen wir uns den einfachen Fall ansehen, bei dem die diagonal zueinander liegenden Ecken entfernt werden. Wir haben nun also 62 Felder, die wir mit 31 Dominosteinen abdecken wollen. Nun kann man versuchen das verkleinerte Schachbrett zu überdecken. Das muss allerdings unweigerlich scheitern, denn wir haben zwei Felder der gleichen Farbe entfernt. Dominosteine liegen allerdings immer auf einem schwarzen und einem weißen Feld. Dadurch bleiben bei jedem Versuch zwei Felder der gleichen Farbe übrig. Das heißt bei abgeschnittenen Schachbrettern muss immer die gleiche Anzahl an weißen und schwarzen Feldern enthalten sein um ein überdeckbares Schachbrett zu erhalten.
Die Kasteleyn-Fisher-Temperley-Formel
Diese Formel wurde 1961 entwickelt und beschreibt die Anzahl [math]B(m,n)[/math] der möglichen Belegungen eines rechteckigen [math]m \times\ n[/math] - Schachbrettes.
[math]B(m,n) = \prod_{j=1}^{\lceil \frac{m}{2}\rceil}\prod_{k=1}^{\lceil \frac{n}{2}\rceil}\left(4\cos^2{\frac{j\pi}{m+1}}+4\cos^2{\frac{k\pi}{n+1}}\right)[/math]
Beispiel der Anwendung dieser Formel anhand eines [math] 2 \times 4[/math]- Schachbretts:
[math]B(2,4)=\ \prod_{j=1}^\frac{2}{2}\prod_{k=1}^\frac{4}{2}\left(4\cos^2{\frac{j\pi}{2+1}}+4\cos^2{\frac{k\pi}{4+1}}\right)=\ \prod_{j=1}^{1}\prod_{k=1}^{2}\left(4\cos^2{\frac{j\pi}{3}}+4\cos^2{\frac{k\pi}{5}}\right)[/math]
Nach Auflösen der Produkte ergibt sich:
[math]B(2,4)=\left(4{cos}^2{\frac{1\pi}{3}}+4{cos}^2{\frac{1\pi}{5}}\right)\left(4{cos}^2{\frac{1\pi}{3}}+4{cos}^2{\frac{2\pi}{5}}\right) = {5}[/math]
Somit gibt es in diesem Beispiel 5 mögliche Belegungen des Schachbretts. Für das gewöhnliche [math] 8 \times 8[/math]-Schachbrett erhalten wir für die Anzahl an möglichen Überdeckungen: [math] 12.988.816[/math]
Wenn m und n ungerade Zahlen sind, so hat auch das Schachbrett eine ungerade Anzahl an Feldern und kann deshalb nicht gekachelt werden. Die Formel ergibt für diesen Fall immer den Wert 0.
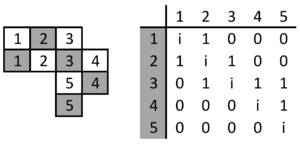
Nun wird die Funktionsweise dieser Formel anhand eines Prinzips verdeutlicht, welches nicht nur für rechteckige Schachbretter, sondern allgemein gültig ist. Hier muss lediglich die Anzahl der schwarzen und weißen Felder identisch sein und kein Loch enthalten sein.
In der Abbildung rechts ist als Beispiel ein zufälliges und nicht rechteckiges Schachbrett dargestellt. Zunächst werden jeweils die schwarzen und weißen Felder durchgezählt. Die Positionierung der Zahlen spielt hierbei keine Rolle. Anschließend werden alle direkt aneinander liegenden Zahlen in der nebenstehenden Tabelle markiert. Diagonal zueinander befindliche Felder sind hierbei ausgeschlossen. Alle in Verbindung stehenden Zahlen werden mit einer 1 markiert. Sind die beiden Zahlen identisch, so werden sie in der Tabelle mit der imaginären Zahl i versehen. Die restlichen Einträge der Tabelle werden auf Null gesetzt.
Die entstandene Tabelle kann nun direkt in eine Matrix übernommen werden, aus deren Determinante man die Anzahl der möglichen Belegungen des Schachbrettes ablesen kann.
[math]\det K = \det \left(\begin{matrix}i&1&0&0&0\\1&i&1&0&0\\0&1&i&1&1\\0&0&0&i&1\\0&0&0&0&i\\\end{matrix}\right) = {3i}[/math]
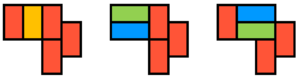
Das Vorzeichen und die imaginäre Zahl i sind bei den jeweiligen Ergebnissen zu vernachlässigen. Somit beträgt die Anzahl der möglichen Belegungen in unserem Beispiel 3.
Die unterschiedlichen Möglichkeiten für dieses Beispiel werden in nebenstehender Abbildung dargestellt. Wir wollen nun eine kurze Erklärung geben wie dieser Trick funktioniert. Wir erinnern uns an die bekannte Leibnitz-Formel für die Determinante:
[math]\det K = \sum_{\sigma \in S_5} sgn(\sigma) \prod_{i = 1}^{n} K_{i, \sigma(i)} [/math]
Man kann sich jetzt überlegen, dass jede Permutation [math] \sigma[/math] versucht ein schwarzes mit einem weißen Feld zu vereinigen. Ist dies für alle Felder möglich erhalten wir einen Summanden der ungleich Null ist. Es kann nun gezeigt werden, dass diese Summanden alle von der gleichen Art sind, also alle [math] 1[/math], [math] -1[/math] oder [math] i[/math]. Somit zählt die Determinante, wie viele der Permutationen möglich sind und der Betrag der Determinante gibt die Anzahl wieder. Der Zusammenhang mit der Kasteleyn-Fischer-Temperly-Formel besteht nun darin, dass es sich bei dem Matrix-Trick um eine Verallgemeinerung handelt. Es kann gezeigt werden, dass für reckeckige Schachbretter die Terme in der Formel gerade die Eigenwerte der Matrix [math] \left(\begin{matrix} 0 & K\\ K' & 0 \\\end{matrix} \right)[/math] sind.
Berechnet man die mögliche Anzahl an Belegungen der [math]2\times n[/math]-Schachbretter in aufsteigender Reihenfolge, so erhält man die Fibonacci Folge.
Aztekendiamanten
Definition der Aztekendiamanten
Wir betrachten beim Arctic Circle Theorem oder dem Aztek Diamond nun Schachbretter, bei denen nicht nur 2 Felder entfernt wurden, sondern im allgemeinen [math]n((n/2)-1)[/math] Felder an allen vier Ecken entfernt wurden, sodass eine Raute in Pixelgraphik entsteht. Somit hat das Feld nur noch [math]n((n/2)+1)[/math] Feldern. Dabei ist die Feldgröße angegeben in der maximalen Kästchenweite der Diagonale.
Die Felder haben dann folgendes Aussehen:
- Feldgröße 2 x 2 besteht aus 2 schwarzen 2 weißen Feldern
- Feldgröße 4 x 4 besteht aus 6 schwarzen 6 weißen Feldern
- Feldgröße 6 x 6 besteht aus 12 schwarzen 12 weißen Feldern
- Feldgröße 8 x 8 besteht aus 20 schwarzen 20 weißen Feldern
- ...
- Feldgröße [math]n \times n [/math] für [math]n \geq 2 [/math] besteht aus [math]n((n/2)+1)/2[/math] schwarzen und [math]n((n/2)+1)/2[/math] weißen Feldern.
Auch hier bestehen die Felder aus jeweils gleichvielen verschiedenfarbigen Feldern, da sonst die Überdeckung mit Dominosteinen nicht möglich ist, wie oben Bewiesen. n ist hier immer gerade, da bei den Feldern die mit 2 begonnen wird und an allen Seiten neue Kästchen hinzugelegt wird. Also nach der Form Feldgröße = 2n mit [math]n \in \mathbb{N}[/math].
Das Arctic Circle Theorem
In der kombinatorischen Mathematik bestehen Aztekendiamanten der Kardinalität (Ordnung) n aus allen Quadraten, deren Zentrum (x,y), die Gleichung [math]|x|+|y|\lt =n[/math] erfüllen. Wir bezeichnen den n-ten Aztekendiamant mit [math]A(n)[/math]. Die Anzahl wie oft man ein Aztec-Diamond der Ordnung [math]n[/math] legen kann ist [math]2^{\frac{n(n+1)}{2}}[/math]. Das Arctic Circle Theorem sagt nun, dass wenn n größer wird und damit die Anzahl der möglichen Überdeckungen größer wird, die Wahrscheinlichkeit, dass die Ecken des Diamanten jeweils in einer Farbe sind und sich in der Mitte eine kreisförmige chaotische Region befindet gegen 1 geht. Das heißt es gibt nur noch vernachlässigbar wenige Überdeckungen gibt die eine andere Struktur besitzen. Desweiteren kann für den Grenzfall [math]n \rightarrow \infty[/math] gezeigt werden, dass sich die chaotische Mitte im Mittel einem perfekten Kreis annähert. Jedes Domino wird genau ein schwarzes und ein weißes Feld treffen. Die Farben werden dann so festgelegt, je nachdem ob rechts, links oder oben, unten weiß oder schwarz ist.
Tanzende Dominosteine
Um einen zufällig gefärbten Aztekendiamanten zu erhalten gibt es verschiedene Methoden. Einfach ein gegebenes Schachbrett zu färben ist leider keine praktikable Möglichkeit, da die Wahrscheinlichkeiten für jedes Feld und im Allgemeinen auch für jede Fabe unterschiedlich sind und nicht 25% betragen. Eine Möglichkeit wäre es jedoch zum Beispiel viele Diamanten in der gewünschten Größe zu erstellen und jeden dieser Diamanten mit einer möglichen Kombination an Dominosteinenen bedecken, sodass alle möglichen Kombinationen einmal vorkommen. Aus dieser Menge könnte dann ein zufälliger Aztekendiamant gezogen werden. Das Problem ist, dass auch diese Methode sehr (rechen-)aufwendig ist.
Eine bessere Methode ist die sogenannte Square-Dance-Methode. Hierbei werden ausgehend vom einfachsten Diamanten [math] A(1)[/math], ( ein [math] 2 \times 2[/math] Quadrat) schrittweise beliebig große Aztenkendiamanten aufgebaut. Hierbei wird jeweils eine Farbe mit einer Richtung assoziiert, im Beispiel rechts entspricht blau nach oben.
Der Square-Dance-Algorithmus lautet:
- [math] 2 \times 2[/math] Diamant zufällig mit zwei Dominosteinen belegen.
- Den Diamant um eine Ordung erweitern.
- Prüfen ob zwei Felder aufeinander zeigen, da hier kein Verschieben möglich wäre, diese Felder entfernen.
- Die Dominosteine in die zu den Farben gehörigen Richungen verschieben.
- Die resultierenden [math] 2 \times 2[/math] Felder zufällig belegen.
- zurück zu Schritt 2 gehen.
Anhand dieses Vorgehens ist es recht einfach zu sehen wie der Arctic Circle und vor allem die stabilen Ecken entstehen.
Arktischer Kreis und stabile Ecken
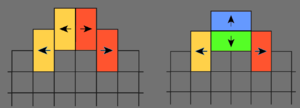
Anhand obigen Vorgehens ist es recht einfach zu sehen, aber doch sehr erstaunlich, wie trotz des von Anfang an zufälligen Vorgehens, ein Aztekendiamant mit einigen sehr stabilen und geordeneten Regionen entsteht. Das erste Merkmal ist schon nach nur wenigen Iterationen sichtbar, nämlich die stabilen Ecken. Diese Struktur entsteht, da eine Ecke, z.B. oben, entweder:
- mit zwei Dominosteinen, die nach rechts und links zeigen ausgefüllt ist, oder
- mit einem nach oben zeigendem Stein.
Im ersten Fall, entseht im nächsten Iterationsschritt in der oberen Ecke ein freies [math] 2 \times 2[/math] Feld, was wieder entweder mit 1. oder 2. gefüllt wird. Im zweiten Fall jedoch verschiebt sich der blaue Stein jedoch nach oben und sitzt wieder in der oberen Ecke. Da für den ersten Fall im nächsten Schritt die Wahrscheinlichkeiten für beide Fälle 50/50 sind, wird irgendwann Fall 2. eintreten. Dieser Stein blockiert dann dauerhaft die obere Ecke. Das selbe Prinzip sorgt dafür, dass unterhalb dieser Spitze sich nach und nach ein immer größer werdendes Feld an gleichen Steinen ansammelt. Dies gilt natürlich für alle Ecken, sodass das charateristisches "Eis" in den Ecken entsteht.
Diese stabile Verschieben in die Ecken sorgt außerdem für einen weiteren Effekt, nämlich dass in der Mitte des Diamanten ein Kreis von ungeordneten Dominosteinen entsteht. Dies ist der Arktische Kreis, der Namensgeber des Arctic Circle Theorem. Das Arctic Circle Theorem besagt weiter, dass die zentrale Region für steigendes n sich einem Kreis annähert. Dieser hat den Radius [math] \frac{n}{\sqrt{2}}[/math].
Anzahl der Überdeckungen
Nachdem wir nun den Tanz der Dominosteine verstanden haben, wollen wir nun die Anzahl der Überdeckungen für einen beliebigen Aztekendiamant [math] A(n)[/math] berechnen. Wir beginnen mit [math] A(1)[/math] und sehen ein, dass es für diesen genau zwei Überdeckungen gibt. Ausgehend von einer dieser Möglichkeiten schieben wir nun im erweiterten [math] A(2)[/math] die Dominosteine in die durch den Pfeil angezeigte Richtung. Es bleiben nun zwei 4x4 Felder frei, die auf [math] 2^2[/math] Weisen überdeckt werden können. Dies ist das zentrale Argument im rigorosen Beweis der Aussage. Es kann nämlich analog zu unseren Überlegungen gezeigt werden, dass im k-ten Schritt [math] 2^{k}[/math] Möglichkeiten hinzukommen. Insgesamt erhalten wir also für den [math] A(n)[/math] genau [math] 2^{1} \cdot 2^{2} \cdot ... \cdot 2^{n} = 2^{1 + 2 + 3 + ... + n} = 2^{\frac{n(n+1)}{2}}[/math] mögliche Überdeckungen.
[math] [/math]
Quellen
- Sciencia, Librero, ISBN: 978-90-8998-430-2, Seite 14f.
- Fermats letzter Satz, Simon Singh, dtv, ISBN: 978-3-423-33052-7, Seite 44-50
- Dimers and Dominoes, James Propp, arXiv:1405.2615
Weiterführende Literatur
- https://link.springer.com/article/10.1023/A:1008605912200
- https://archive.org/details/arxiv-math9801068/mode/2up
- http://www.issmys.eu/scientific-information/lectures-notes/the-arctic-circle-by-vincent-beffara
- https://www.youtube.com/watch?v=Yy7Q8IWNfHM
Autoren
- Alexander Fichtelmann
- Julian Groth
- Steven Göbl
- Alicia Trabold