Fibonacci Folge

Die Fibonacci Folge ist eine Folge natürlicher Zahlen. Konstruiert wird sie durch folgende, rekursive Bildungsvorschrift:

[math] f_{n}=f_{n-1}+f_{n-2} [/math]

mit den Startwerten [math] f_1=f_2=1 [/math].

[math] \begin{array}{c|c|c|c|c|c|c|c|c|c} f_{1} & f_{2} & f_{3} & f_{4} & f_{5} & f_{6} & f_{7} & f_8 & f_9 & f_{10}\\\hline 1 & 1 & 2 & 3 & 5 & 8 & 13 & 21 & 34 & 55 \end{array} \cdots [/math]

Verhältnis zweier aufeinanderfolgender Fibonacci-Zahlen

Die Folge [math] \left(\frac{f_{n+1}}{f_n}\right)_{n\in\mathbb{N}} [/math] der Verhältnisse zweier aufeinanderfolgender Fibonacci-Zahlen konvergiert in [math]\mathbb{R}[/math] mit folgendem Grenzwert:

[math]\lim_{n\to\infty}\frac{f_{n+1}}{f_n}=\frac{1+\sqrt{5}}{2}:=\Phi[/math]

[math]\Phi[/math] wird auch Goldener Schnitt genannt.

Beweis

Diese Behauptung lässt sich leicht mit der weiter unten bewiesenen Formel von Moivre und Binet beweisen: [math] \begin{array}{rcl} \frac{f_{n+1}}{f_n}&=&\frac{\frac{\Phi^{n+1}-(1-\Phi)^{n+1}}{\sqrt{5}}}{\frac{\Phi^n-(1-\Phi)^n}{\sqrt{5}}} =\frac{\Phi^{n+1}-(1-\Phi)^{n+1}}{\Phi^n-(1-\Phi)^n} & \end{array} [/math] Da [math]|1-\Phi|\lt 1 [/math] fällt dieser Teil im Limes weg und es gilt: [math] \begin{array}{rcl} \lim_{n\to\infty}\frac{f_{n+1}}{f_n}&=&\lim_{n\to\infty}\frac{\Phi^{n+1}-(1-\Phi)^{n+1}}{\Phi^n-(1-\Phi)^n}\\ &=&\lim_{n\to\infty}\frac{\Phi^{n+1}}{\Phi^n}=\Phi \end{array} [/math]

Kaninchen-Aufgabe

Eine Anwendungsbeispiel findet die Fibonacci Folge bei der Kaninchenpopulation.

Es startet ein männliches und ein weibliches Kaninchenneugeborenes (ein Paar). Angenommen ein Neugeborenes braucht ein Monat um auszuwachsen, ein Paar bekommt pro Monat ein Paar Neugeborenes und kein Kaninchen stirbt.

Im ersten Monat sind es also ein Paar Neugebore, im 2. Monat sind sie Erwachsen, also keine Neugeborenen. Dann bekommen sie ein Paar Neugeborene im dritten Monat und so weiter.

Es gibt also im ersten Monat keine Erwachsenen, im zweiten Monat dann ein Paar Erwachsene, 3. Monat 1 Paar, im vierten Monat 2 Paare und so weiter.

Wenn man sich nun also die Gesamtpopulation anguckt folgt:

[math] \begin{align*} \begin{array}[h]{l|c|c|c|c|c|c}     Monat & 1 & 2 & 3 & 4 & 5 & 6\\     \hline     Erwachsene & 0 & 1 & 1 & 2 & 3 & 5 \\     \hline     Neugeborene & 1 & 0 & 1 & 1 & 2 & 3 \\     \hline     Gesamt & 1 & 1 & 2 & 3 & 5 & 8\\     \end{array} \end{align*} [/math]

Hier in dem vereinfachten Beispiel beschreibt also die Fibonacci Folge die Gesamtpopulation der Kaninchen, sowie die jeweiligen Populationen der erwachsenen Kaninchen ab dem zweiten Monat, bzw. auch die neugeborenen Population der Kaninchen ab dem dritten Monat.

Matrixdarstellung

Man kann die Fibonacci Folge auf verschiedene Weisen darstellen. Hier ein Beispiel für die Darstellung in einer Matrix:

[math]\begin{align*} \left( \begin{array}{cc}    f_{n+1}& f_n \\     f_n & f_{n-1} \end{array} \right) = \left( \begin{array}{cc}    1&1 \\     1&0 \end{array} \right)^n \end{align*}[/math]

Die n-te potenz der Matrix [math]A = \left( \begin{array}{cc} 1&1 \\1&0 \end{array} \right)[/math] gibt die n-te Fibonaccizahl auf der Gegendiagonalen an, aufgrund der Matrixmultiplikation.

Pisano-Folge

Betrachten wir nun eine Folge modulo einer Primzahl [math]p \in \mathbb{P} [/math], d.h. über dem Restklassenkörper [math] \mathbb{Z}/_{p\mathbb{Z}} [/math] Nun gucken wir uns die Fibonaccifolge: 0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368,121393,196418,317811,514229,832040,1346269 über dem Restklassenkörper [math] \mathbb{Z}/_{7\mathbb{Z}} [/math] an. Wir erhalten: 0,1,1,2,3,5,1,6,0,6,6,5,4,2,6,1,0,1,1,2,3,5,1,6,0,6,6,5,4,2,6,1,0

Wir sehen, dass die Folge sich nach 16 Werten wiederholt. Außerdem ist die Restklassenfolge wieder eine Fibonaccifolge, da [math]f_n=f_{n-1}+f_{n-2}[/math] man braucht also nicht die Restklasse von jeder einzelnen Werte der Fibonaccifolge in [math]\mathbb{Z}[/math] bilden, sondern kann die Folge direkt in der Restklasse bilden

Auf [math]\mathbb{Z}/_{2\mathbb{Z}}[/math] wiederholt sich die Folge nach 3 Schritten: 0,1,1....

[math]\mathbb{Z}/_{3\mathbb{Z}}[/math] nach 8 Schritten: 0,1,1,2,0,2,2,1,0....

Erweiterung

Die Bildungsvorschrift lässt sich einfach umstellen:

[math] f_{n}=f_{n+2}-f_{n+1} [/math]

Damit erhält man eine erweiterte Fibonacci-Folge:

[math] \cdots\begin{array}{c|c|c|c|c|c|c|c|c|c|c|c|c|c|c} f_{-7} & f_{-6} & f_{-5} & f_{-4} & f_{-3} & f_{-2} & f_{-1} & f_0 & f_1 & f_2 & f_3 & f_4 & f_5 & f_6 & f_7\\\hline 13 & -8 & 5 & -3 & 2 & -1 & 1 & 0 & 1 & 1 & 2 & 3 & 5 & 8 & 13 \end{array} \cdots [/math]

Die Beträge der Werte sind symmetrisch, im Negtiaven alternieren sie jedoch:

[math] f_{-n}=(-1)^{n+1}f_n[/math]

Dementsprechend nähert sich das Verhältnis zweier aufeinanderfolgender Fibonacci-Zahlen im Negativen gegen [math] -\frac{1}{\Phi} [/math] an.

Bei der Fibonacci-Folge sind die ersten beiden Glieder 1. Also [math]f_1 = f_2 = 1[/math]. Damit ist die Fibonaccifolge vollständig definiert. Eine andere Folge erhält man, wenn man [math]f_1 = 2[/math] und [math]f_2 = 1[/math] nimmt. Diese Folge wird auch Lucas-Folge genannt:

[math] \cdots\begin{array}{c|c|c|c|c|c|c|c|c|c|c|c|c|c|c} f_{-7} & f_{-6} & f_{-5} & f_{-4} & f_{-3} & f_{-2} & f_{-1} & f_0 & f_1 & f_2 & f_3 & f_4 & f_5 & f_6 & f_7\\\hline 47 & -29 & 18 & -11 & 7 & -4 & 3 & -1 & 2 & 1 & 3 & 4 & 7 & 11 & 18 \end{array} \cdots [/math]

Diese Folge ist nicht mehr betragsmäßig symmetrisch zu [math]f_0[/math] sondern zu [math]f_1[/math]:

[math] f_{-n-1}=(-1)^{n}f_{n-1} [/math]

Das Verhältnis zweier aufeinanderfolgender Lucas-Zahlen nähert sich im Unendlichen ebenfalls gegen [math]\Phi[/math] (bzw. [math]-\frac{1}{\Phi}[/math] im Negativen) an.

Kontinuierliche Fibonacci-Funktion

Formel von Moivre-Binet

Die Formel von Moivre und Binet ist eine Formel zur expliziten Berechung der n-ten Fibonacci-Zahl:

[math] \begin{array}{rcl} f:\mathbb{N}&\to&\mathbb{N}\\ n&\mapsto&f_n=\frac{\Phi^n-(1-\Phi)^n}{\sqrt{5}} \end{array} [/math]

[math]\Phi[/math] ist dabei der Goldener Schnitt [math]\Phi=\frac{1+\sqrt{5}}{2}[/math]. Diese Formel liefert für ganzzahlige Werte für n auch exakte, ganzzahlige Ergebnisse.

Beweis durch vollständige Induktion

Um zu zeigen, dass diese Formel die Fibonacci-Zahlen ergibt, überprüfen wir die Bildungsvorschrift: IA: Die Formel gilt für [math]n=0\ \left(\frac{\Phi^0-(1-\Phi)^0}{\sqrt{5}}=\frac{1-1}{\sqrt{5}}=0=f_0\right)[/math] und für [math] n=1\ \left( \frac{\Phi^1-(1-\Phi)^1}{\sqrt{5}}=\frac{\sqrt{5}}{\sqrt{5}}=1=f_1\right)[/math]. IV: Nun gelte sie für ein [math] n,\ n-1\in\mathbb{N}[/math]. IS: Dann gilt: [math] \begin{array}{rl} f_{n+1}=f_{n}+f_{n-1}&=\frac{\Phi^n-(1-\Phi)^n+\Phi^{n-1}-(1-\Phi)^{n-1}}{\sqrt{5}}\\ &=\frac{\Phi^{n-1}(1+\Phi)-(1-\Phi)^{n-1}\left(1+(1-\Phi)\right)}{\sqrt{5}}\\ &=\frac{\Phi^{n-1}(\Phi^2)-(1-\Phi)^{n-1}(1-\Phi)^2}{\sqrt{5}}\\ &=\frac{\Phi^{n+1}-(1-\Phi)^{n+1}}{\sqrt{5}} \end{array} [/math] Ebenso für negative Zahlen: [math] \begin{array}{rl} f_{n-2}=f_{n}-f_{n-1}&=\frac{\Phi^n-(1-\Phi)^n-\Phi^{n-1}+(1-\Phi)^{n-1}}{\sqrt{5}}\\ &=\frac{\Phi^{n-1}(\Phi-1)-(1-\Phi)^{n-1}\left((1-\Phi)-1\right)}{\sqrt{5}}\\ &=\frac{\Phi^{n-1}\left(\frac{1}{\Phi}\right)-(1-\Phi)^{n-1}\left(\frac{1}{1-\Phi}\right)}{\sqrt{5}}\\ &=\frac{\Phi^{n-2}-(1-\Phi)^{n-2}}{\sqrt{5}} \end{array} [/math]

Erweiterung auf eine kontinuierliche Funktion

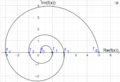
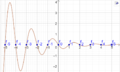
Nun stellt sich die Frage was passiert, wenn wir in die Formel von Moivre-Binet nicht-ganzzahlige Werte für n einsetzen, die Fibonacci-Folge also in eine kontinuierliche Funktion umwandeln. Da [math]1-\Phi[/math] jedoch negativ ist, und nicht-ganzzahlige Potenzen von negativen Zahlen nur im Komplexen definiert sind, müssen wir den Wertebereich auf [math]\mathbb{C}[/math] erweitern:

[math] \begin{array}{rl} f:&\mathbb{R}\to\mathbb{C}\\&x\mapsto f(x)=\frac{\Phi^x-(1-\Phi)^x}{\sqrt{5}} \end{array} [/math]

Der Graph dieser Funktion sieht wie folgt aus (Darstellung als Kurve mit Kurvenparameter x):

• 

  [math] -5\leq x\leq0[/math]

• 

  [math] 0\leq x\leq5[/math]

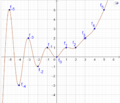
Eine andere Darstellung sieht wie Folgt aus:

• 

  Imaginärteil der Moivre-Binet-Funktion

• 

  Realteil der Moivre-Binet-Funktion

Kompexe Fibonacci-Funktion

Wir haben bereits gesehen, dass wir die Fibonaccifolge zu einer komplexwertige Funktion mit reellen Eingabewerten erweitern können. Nun können wir dieses Konzept noch weiter abstrahieren, indem wir auch komplexe Eingabewerte zulassen:

[math] \begin{array}{rl} f:&\mathbb{C}\to\mathbb{C}\\&z\mapsto f(z)=\frac{\Phi^z-(1-\Phi)^z}{\sqrt{5}} \end{array} [/math]

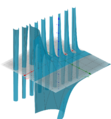
Da die Darstellung komplexer Funktionen immer etwas kompliziert ist, zeigen wir mehrere Darstellungsmöglichkeiten:

• 

  Darstellung mittels Domain colouring

Bei einer anderen Art der Darstellung stellt man den Real- und Imaginärteil der Funktionswerte als Funktionen [math] \mathbb{R}^2\to\mathbb{R} [/math] dar. Im Folgenden ist dies mit dem Funktionen-Plotter Geogebra dargestellt (Bemerkung: Da Geogebra keine sonderlich exakte Berechnung ermöglicht, sind diese Bilder etwas ungenauer):

• 

  Realteil

• 

  Imaginärteil

• 

  Betrag

Interaktive Darstellung mittels Geogebra:

https://www.geogebra.org/m/qhrggvtr

Nullstellen

Wie man bereits anhand der Bilder (mehr oder weniger gut) erkennen kann, liegen alle Nullstellen auf einer Gerade durch den Nullpunkt. Genauer lassen sich alle Nullstellen [math]z_n[/math] darstellen als:

[math]z_n=n\cdot\frac{2\pi i}{\ln(\Phi)-\ln(1-\Phi)}\qquad n\in\mathbb{Z}[/math]

Beweis

Es gilt: [math] \begin{array}{rcll} f(z)=\frac{\Phi^z-(1-\Phi)^z}{\sqrt{5}}&=&0&\\ \Phi^z&=&(1-\Phi)^z&\\ z\cdot\ln(\Phi)&=&z\cdot\ln(1-\Phi)+2\pi n i&\qquad n\in\mathbb{Z}\\ z&=&n\cdot\frac{2\pi i}{\ln(\Phi)-\ln(1-\Phi)}&\qquad n\in\mathbb{Z} \end{array} [/math]

Autoren

Ines Christa, Konrad Kockler, Sebastian Splitthoff, Dennis Straub