Goldener Schnitt: Unterschied zwischen den Versionen
Seb Sp (Diskussion | Beiträge) |
|||
| (66 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
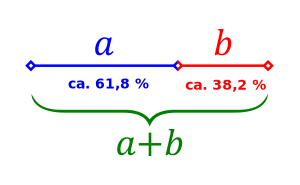
Der "Goldene Schnitt" bezeichnet allgemein ein spezielles Teilungsverhältnis einer Strecke. | Der "Goldene Schnitt" bezeichnet allgemein ein spezielles Teilungsverhältnis einer Strecke. | ||
| − | Die Besonderheit dieses Verhältnisses besteht darin, die Gesamtstrecke in zwei Teile aufzuteilen, wobei die Gesamtstrecke dasselbe Teilungsverhältnis zur größeren Teilstrecke aufweist, wie auch die größere Teilstrecke zur kleineren Teilstrecke. | + | Die Besonderheit dieses Verhältnisses besteht darin, die Gesamtstrecke in zwei Teile aufzuteilen, wobei die Gesamtstrecke dasselbe Teilungsverhältnis zur größeren Teilstrecke aufweist, wie auch die größere Teilstrecke (Major) zur kleineren Teilstrecke (Minor). |
[[Datei:GS formatiert.png|alternativtext=|mini|300x300px|Proportionen des Goldenen Schnitts]] | [[Datei:GS formatiert.png|alternativtext=|mini|300x300px|Proportionen des Goldenen Schnitts]] | ||
Den Quotient der Strecken nennt man die Goldene Zahl <math>\Phi</math>. | Den Quotient der Strecken nennt man die Goldene Zahl <math>\Phi</math>. | ||
== Herleitung des Goldenen Schnitts == | == Herleitung des Goldenen Schnitts == | ||
| − | Die obige Definition lässt sich algebraisch ausdrücken und wie folgt eindeutig lösen | + | Die obige Definition lässt sich algebraisch ausdrücken und wie folgt eindeutig lösen, wobei a (Major) und b (Minor) die Teilstrecken und a+b die Gesamtstrecke ist. |
<br /> | <br /> | ||
| − | ::<math> \Phi = \frac{a}{b} = \frac{a+b}{a} = 1+\frac{b}{a} = 1 + \frac{1}{\Phi}\\\\ </math> | + | ::<math> \Phi = \frac{a}{b} \overset{!}{=} \frac{a+b}{a} = 1+\frac{b}{a} = 1 + \frac{1}{\Phi}\\\\ </math> |
::<math> \Leftrightarrow \Phi^{2} = \Phi + 1 \\\\ </math> | ::<math> \Leftrightarrow \Phi^{2} = \Phi + 1 \\\\ </math> | ||
| Zeile 16: | Zeile 16: | ||
::<math> \Leftrightarrow 0 = \Phi^{2} - \Phi - 1 \\\\ </math> | ::<math> \Leftrightarrow 0 = \Phi^{2} - \Phi - 1 \\\\ </math> | ||
| − | ::<math> \Rightarrow \Phi_{1} = \frac{1+\sqrt[]{5}}{2} \approx 1,618\\ </math> | + | ::<math> \Rightarrow \Phi_{1} = \frac{1+\sqrt[]{5}}{2} = \Phi \approx 1,618\\ </math> |
| − | ::<math> \Rightarrow \Phi_{2} = \frac{1-\sqrt[]{5}}{2} \approx 0,618 | + | ::<math> \Rightarrow \Phi_{2} = \frac{1-\sqrt[]{5}}{2} = \varphi \approx 0,618 </math> |
| − | Wir nennen <math> \ | + | Wir nennen <math> \Phi </math> die Goldene Zahl bzw. den Goldenen Schnitt, für den gilt: <br /><br /> |
| + | ::<math> \frac{1}{\Phi} = \Phi - 1 = \varphi</math> | ||
| + | <br /> | ||
== <math>\Phi</math> als "irrationalste" Zahl == | == <math>\Phi</math> als "irrationalste" Zahl == | ||
Allgemein gibt es keine irrationale Zahl die "irrationaler" als eine andere irrationale Zahl ist. <math>\Phi</math> lässt sich nur sehr "langsam" durch rationale Zahlen annähern, daher die meist scherzhafte Aussage <math>\Phi</math> sei die "irrationalste" Zahl. | Allgemein gibt es keine irrationale Zahl die "irrationaler" als eine andere irrationale Zahl ist. <math>\Phi</math> lässt sich nur sehr "langsam" durch rationale Zahlen annähern, daher die meist scherzhafte Aussage <math>\Phi</math> sei die "irrationalste" Zahl. | ||
| − | === Kettenbruchdarstellung=== | + | === [https://funfacts.mathi.uni-heidelberg.de/index.php/Euklidischer_Algorithmus_und_Kettenbrüche Kettenbruchdarstellung]=== |
| − | Um die Annäherung durch rationale Zahlen vorzunehmen, stellt man die Zahl als unendlichen Kettenbruch dar und bricht diesen an einer Stelle ab. Je später, desto genauer die Annäherung. | + | Um die Annäherung durch rationale Zahlen vorzunehmen, stellt man die Zahl als unendlichen Kettenbruch dar und bricht diesen an einer Stelle ab. Je später man abbricht, desto genauer die Annäherung. |
| + | |||
| + | <math> \Phi = 1 + \frac{1}{\Phi} = 1 + \frac{1}{1 + \frac{1}{\Phi}} = 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{\Phi}}} = 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{\Phi}}}} \quad ... </math> | ||
| − | |||
:: | :: | ||
Wir sehen nun, dass der Kettenbruch von <math>\Phi</math> nur Einsen als Elemente enthält, woraus sich wiederum folgern lässt, dass der Nenner der Näherung durch rationale Zahlen so langsam wie nur möglich wächst und sich somit eine möglichst genaue Approximation nur schlecht durchzuführen ist. | Wir sehen nun, dass der Kettenbruch von <math>\Phi</math> nur Einsen als Elemente enthält, woraus sich wiederum folgern lässt, dass der Nenner der Näherung durch rationale Zahlen so langsam wie nur möglich wächst und sich somit eine möglichst genaue Approximation nur schlecht durchzuführen ist. | ||
| Zeile 36: | Zeile 39: | ||
Daher die Aussage <math>\Phi</math> sei die irrationalste nur mögliche Zahl. | Daher die Aussage <math>\Phi</math> sei die irrationalste nur mögliche Zahl. | ||
| − | + | Interessant hierbei ist, dass der Näherungsbruch immer aus zwei aufeinanderfolgenden [[Fibonacci Folge|Fibonacci-Zahlen]] besteht. | |
{| class="wikitable mw-collapsible centered" | {| class="wikitable mw-collapsible centered" | ||
|+Annäherung durch Kettenbruchverfahren | |+Annäherung durch Kettenbruchverfahren | ||
| Zeile 51: | Zeile 54: | ||
! rowspan="3" |Die rekursive Bildungsformel lautet: <br /> | ! rowspan="3" |Die rekursive Bildungsformel lautet: <br /> | ||
<big> <math> \frac{p_{n}}{q_{n}} = \frac{p_{n-1} + q_{n-1}}{p_{n-1}} </math> </big> <br /> <br /> | <big> <math> \frac{p_{n}}{q_{n}} = \frac{p_{n-1} + q_{n-1}}{p_{n-1}} </math> </big> <br /> <br /> | ||
| − | ''<small> mit <math> p_{0},q_{0} = 1 </math> </small>'' | + | ''<small> mit <math> p_{0}, q_{0} = 1 </math> </small>'' |
|- | |- | ||
| Zeile 86: | Zeile 89: | ||
=== Innere Teilung === | === Innere Teilung === | ||
{| class="wikitable" | {| class="wikitable" | ||
| − | | style="text-align:center;" |[[Datei:Innere Teilung Klassisch neu.png|alternativtext=|zentriert|mini| | + | | style="text-align:center;" |[[Datei:Innere Teilung Klassisch neu.png|alternativtext=|zentriert|mini|300x300px]] |
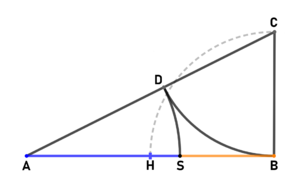
| style="text-align:left;" |<big>'''<u>"klassische Methode" zur inneren Teilung</u>:'''</big> | | style="text-align:left;" |<big>'''<u>"klassische Methode" zur inneren Teilung</u>:'''</big> | ||
Gegeben sei eine beliebige Länge <small><math> \overline{AB}</math></small>. Die Strecke <small><math> \overline{BC}</math></small> steht senkrecht zu <small><math> \overline{AB}</math></small> im Punkt B und hat die Länge <math> \frac{\overline{AB}}{2}</math>. | Gegeben sei eine beliebige Länge <small><math> \overline{AB}</math></small>. Die Strecke <small><math> \overline{BC}</math></small> steht senkrecht zu <small><math> \overline{AB}</math></small> im Punkt B und hat die Länge <math> \frac{\overline{AB}}{2}</math>. | ||
| + | |||
Der Kreis um C mit Radius <small><math> \overline{BC}</math></small> schneidet die Strecke <small><math> \overline{AC}</math></small> im Punkt D. | Der Kreis um C mit Radius <small><math> \overline{BC}</math></small> schneidet die Strecke <small><math> \overline{AC}</math></small> im Punkt D. | ||
Der Kreis um A mit Radius <small><math> \overline{AD}</math></small> teilt die Strecke <small><math> \overline{AB}</math></small> im Verhältnis des Goldenen Schnitts. | Der Kreis um A mit Radius <small><math> \overline{AD}</math></small> teilt die Strecke <small><math> \overline{AB}</math></small> im Verhältnis des Goldenen Schnitts. | ||
| + | |||
| + | '''<u>Beweis</u>:''' | ||
| + | {| class="wikitable mw-collapsible mw-collapsed" | ||
| + | |+ | ||
| + | |- | ||
| + | |<math> \begin{align*} | ||
| + | &a = \overline{AS}\\ | ||
| + | &b = \overline{BS}\\\\ | ||
| + | &k = a+b\\ | ||
| + | &k^2+\left( \frac{k}{2}\right)^2 = \left( a+ \frac{k}{2} \right)^2\\ | ||
| + | &\Leftrightarrow k^2+\frac{k^2}{4} = a^2 + ak+ \frac{k^2}{4} | \text{ ersetze k durch a+b} \\ | ||
| + | &\Leftrightarrow a^2 + 2ab + b^2 = a^2 + a^2 + ab\\ | ||
| + | &\Leftrightarrow b^2 + ab = a^2 \\ | ||
| + | &\Leftrightarrow \frac{a}{b} = \frac{a+b}{a} \text{ Gleichung des Goldenen Schnitts} | ||
| + | \end{align*} | ||
| + | </math><ref>Funfacts Vorlesung; Universität Heidelberg; Wintersemester 20/21</ref> | ||
| + | |} | ||
|- | |- | ||
| − | | style="text-align:center;" |[[Datei:Innere Teilung Euklid | + | | style="text-align:center;" |[[Datei:Innere Teilung Euklid neue Beschriftung.png|alternativtext=|zentriert|mini|300x300px]] |
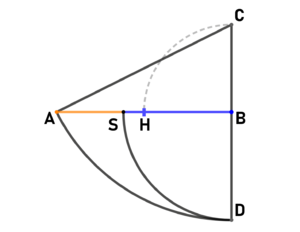
| style="text-align:left;" |<big>'''<u>Methode nach Euklid</u>:'''</big> | | style="text-align:left;" |<big>'''<u>Methode nach Euklid</u>:'''</big> | ||
Gegeben sei eine beliebige Länge <small><math> \overline{AB}</math></small>. | Gegeben sei eine beliebige Länge <small><math> \overline{AB}</math></small>. | ||
Die Strecke <small><math> \overline{BC}</math></small> steht senkrecht zu <small><math> \overline{AB}</math></small> im Punkt B und hat die Länge <math> \frac{\overline{AB}}{2}</math>. | Die Strecke <small><math> \overline{BC}</math></small> steht senkrecht zu <small><math> \overline{AB}</math></small> im Punkt B und hat die Länge <math> \frac{\overline{AB}}{2}</math>. | ||
| − | Der Kreis um | + | |
| + | Der Kreis um C mit Radius <small><math> \overline{AC}</math></small> ergibt Punkt D, welche auf der Verlängerung der Strecke <small><math> \overline{BC}</math></small> liegt. | ||
| + | |||
| + | Der Kreis um B mit Radius <small><math> \overline{BD}</math></small> teilt die Strecke <small><math> \overline{AB}</math></small> im Verhältnis des Goldenen Schnitts. | ||
|} | |} | ||
=== Äußere Teilung === | === Äußere Teilung === | ||
{| class="wikitable" | {| class="wikitable" | ||
| − | | style="text-align:center;" |[[Datei:Äußere Teilung klassisch.png|alternativtext=|zentriert|mini| | + | | style="text-align:center;" |[[Datei:Äußere Teilung klassisch.png|alternativtext=|zentriert|mini|300x300px]] |
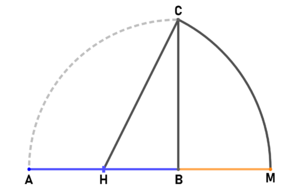
| style="text-align:left;" |<big>'''<u>"klassische Methode" zur äußeren Teilung</u>:'''</big> | | style="text-align:left;" |<big>'''<u>"klassische Methode" zur äußeren Teilung</u>:'''</big> | ||
| − | Gegeben ist eine Strecke <small><math> \overline{AB}</math></small>. Die Strecke <small><math> \overline{BC}</math></small> hat die gleiche Länge wie <small><math> \overline{AB}</math></small> und steht senkrecht auf Punkt B. Der Punkt teilt Strecke <small><math> \overline{AB}</math></small> in der Hälfte. Der Kreis um Punkt H mit Radius <small><math> \overline{ | + | Gegeben ist eine Strecke <small><math> \overline{AB}</math></small>. Die Strecke <small><math> \overline{BC}</math></small> hat die gleiche Länge wie <small><math> \overline{AB}</math></small> und steht senkrecht auf Punkt B. |
| + | |||
| + | Der Punkt H teilt die Strecke <small><math> \overline{AB}</math></small> in der Hälfte. Der Kreis um Punkt H mit Radius <small><math> \overline{HC}</math></small> schneidet die Verlängerung von <small><math> \overline{AB}</math></small> im Punkt M. | ||
| + | |||
| + | Punkt B teilt nun die Strecke <small><math> \overline{AM}</math></small> im goldenen Schnitt. | ||
| + | |||
| + | '''<u>Beweis</u>:''' | ||
| + | |||
| + | {| class="wikitable mw-collapsible mw-collapsed" | ||
| + | |+ | ||
| + | |- | ||
| + | |<math> \begin{align*} | ||
| + | &a = \overline{AB}\\ | ||
| + | |||
| + | &b = \overline{BM}\\\\ | ||
| + | |||
| + | &\Rightarrow \overline{CH} = \sqrt{\left(\frac{a}{2}\right)^2+a^2} = \sqrt{\frac{5 a^2}{4}} = \sqrt{\frac{5}{4}}a\\ | ||
| + | |||
| + | &\Rightarrow k = a + b = \frac{a}{2} + \sqrt{\frac{5}{4}}a= a + \sqrt{\frac{5}{4}} a - \frac{a}{2}a \\ | ||
| + | |||
| + | &\Rightarrow \frac{a}{b} = \frac{a}{\sqrt{\frac{5}{4}}a-\frac{a}{2}} = \frac{1}{\sqrt{\frac{5}{4}}-\frac{1}{2}} = \frac{2}{\sqrt{5} -1 }= \Phi \end{align*}</math> | ||
| + | |||
| + | |} | ||
|- | |- | ||
| − | | style="text-align:center;" |[[Datei:Äußere Teilung George (2).png|alternativtext=|zentriert|mini| | + | | style="text-align:center;" |[[Datei:Äußere Teilung George (2).png|alternativtext=|zentriert|mini|300x300px]] |
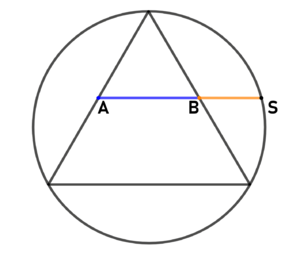
| style="text-align:left;" |<big>'''<u>Methode nach George Odom</u>:'''</big> | | style="text-align:left;" |<big>'''<u>Methode nach George Odom</u>:'''</big> | ||
| − | Gegeben sei ein gleichseitiges Dreieck mit Umkreis. Teilt man nun zwei Seiten des Dreiecks in der Mitte und verbindet die Punkte (A, B) so ergibt die Verlängerung von <small><math> \overline{AB}</math></small> einen Schnittpunkt S mit dem Umkreis. Punkt B teilt nun die Strecke <small><math> \overline{AS}</math></small> im goldenen Schnitt. | + | Gegeben sei ein gleichseitiges Dreieck mit Umkreis. |
| + | |||
| + | Teilt man nun zwei Seiten des Dreiecks in der Mitte und verbindet die Punkte (A, B) so ergibt die Verlängerung von <small><math> \overline{AB}</math></small> einen Schnittpunkt S mit dem Umkreis. | ||
| + | |||
| + | Punkt B teilt nun die Strecke <small><math> \overline{AS}</math></small> im goldenen Schnitt. | ||
|} | |} | ||
| Zeile 120: | Zeile 170: | ||
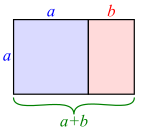
Unter einem Goldenen Rechteck verstehen wir das Rechteck mit dem Seitenverhältnis des Goldenen Schnittes. <ref>Walser, Hans, Der Goldene Schnitt, Eagle Einblicke, Leipzig, 2009, 5.Auflage, Seite 39</ref>Das bedeutet die Seiten a und b stehen im Verhältnis <math> \frac{a}{b} = \frac{a+b}{a} \\ </math>. | Unter einem Goldenen Rechteck verstehen wir das Rechteck mit dem Seitenverhältnis des Goldenen Schnittes. <ref>Walser, Hans, Der Goldene Schnitt, Eagle Einblicke, Leipzig, 2009, 5.Auflage, Seite 39</ref>Das bedeutet die Seiten a und b stehen im Verhältnis <math> \frac{a}{b} = \frac{a+b}{a} \\ </math>. | ||
| − | Konstruiert wird das Goldene Rechtecks durch eine abgewandelte Form der Konstruktion. | + | Konstruiert wird das Goldene Rechtecks durch eine abgewandelte Form der äußeren Konstruktion. Gegeben haben wir eine Strecke a, aus welcher wir ein Quadrat konstruieren. Wie oben beschrieben wird zur Teilstrecke a die Teilstrecke b im Goldenen Schnitt konstruiert. Nun haben wir das Quadrat mit der Seitenlänge a und die Teilstrecke b, was wir nun zu einem Goldenen Rechteck ergänzen können. <ref>Walser, Hans, Der Goldene Schnitt, Eagle Einblicke, Leipzig, 2009, 5.Auflage, Seite 39</ref> |
Eine Besonderheit des Goldenen Rechtecks ist, dass man immer ein Goldenes Rechteck erhält wenn man von einem Goldenen Rechteck ein größtmögliches Quadrat abschneidet. In dem Bild gibt also das kleinere rote Rechteckt wieder ein Goldenes Rechteck. Dies kann beliebig oft wiederholt werden. <ref>Walser, Hans, Der Goldene Schnitt, Eagle Einblicke, Leipzig, 2009, 5.Auflage, Seite 40</ref> | Eine Besonderheit des Goldenen Rechtecks ist, dass man immer ein Goldenes Rechteck erhält wenn man von einem Goldenen Rechteck ein größtmögliches Quadrat abschneidet. In dem Bild gibt also das kleinere rote Rechteckt wieder ein Goldenes Rechteck. Dies kann beliebig oft wiederholt werden. <ref>Walser, Hans, Der Goldene Schnitt, Eagle Einblicke, Leipzig, 2009, 5.Auflage, Seite 40</ref> | ||
| Zeile 129: | Zeile 179: | ||
=== Goldene Dreiecke === | === Goldene Dreiecke === | ||
| − | [[Datei: | + | [[Datei:Goldene Dreiecke.jpg|alternativtext=|mini|345x345px|Goldene Dreiecke]] |
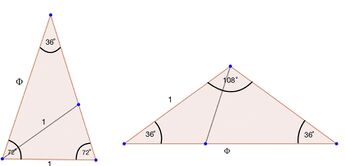
Es gibt zwei unterschiedliche Arten des Goldenes Dreiecks, ein spitzes (erster Art) und ein stumpfes (zweiter Art). Beides sind gleichschenklige Dreiecke, bei denen ein Schenkel zur Grundseite im Goldenen Schnitt steht. <ref>Walser, Hans, Der Goldene Schnitt, Eagle Einblicke, Leipzig, 2009, 5.Auflage, Seite 51</ref> | Es gibt zwei unterschiedliche Arten des Goldenes Dreiecks, ein spitzes (erster Art) und ein stumpfes (zweiter Art). Beides sind gleichschenklige Dreiecke, bei denen ein Schenkel zur Grundseite im Goldenen Schnitt steht. <ref>Walser, Hans, Der Goldene Schnitt, Eagle Einblicke, Leipzig, 2009, 5.Auflage, Seite 51</ref> | ||
| − | Beim Goldenen Dreieck erster Art | + | Beim Goldenen Dreieck erster Art bilden die Schenkel die Majoren, also die längere Teilstrecke, und die Grundseite ist der Minor. Die beiden Winkel die an die Grundseite grenzen haben 72° und der dritte 36°. Das Goldene Dreieck zweiter Art hat zwei Minoren, die Schenkel, und die Basiswinkel haben jeweils 36° während der dritte Winkel 108° hat. <ref>Walser, Hans, Der Goldene Schnitt, Eagle Einblicke, Leipzig, 2009, 5.Auflage, Seite 51</ref> |
Herleitung: Mit <math>\frac{k}{a}=\Phi</math> können wir auch die Winkel im Dreieck berechnen: | Herleitung: Mit <math>\frac{k}{a}=\Phi</math> können wir auch die Winkel im Dreieck berechnen: | ||
| Zeile 153: | Zeile 203: | ||
180° - 90° - 72° = 18° \rightarrow \beta &= 36° \\ | 180° - 90° - 72° = 18° \rightarrow \beta &= 36° \\ | ||
| − | + | ||
\end{align*} | \end{align*} | ||
| Zeile 162: | Zeile 212: | ||
Insbesondere können wir vom Goldenen Dreieck erster Art ein größtmögliches Goldenes Dreieck zweiter Art abschneiden und zurück bleibt ein Goldenes Dreieck erster Art. <ref>Walser, Hans, Der Goldene Schnitt, Eagle Einblicke, Leipzig, 2009, 5.Auflage, Seite 51</ref> | Insbesondere können wir vom Goldenen Dreieck erster Art ein größtmögliches Goldenes Dreieck zweiter Art abschneiden und zurück bleibt ein Goldenes Dreieck erster Art. <ref>Walser, Hans, Der Goldene Schnitt, Eagle Einblicke, Leipzig, 2009, 5.Auflage, Seite 51</ref> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=== Goldener Winkel === | === Goldener Winkel === | ||
| − | [[Datei:01-Goldener Winkel.svg.png|mini| | + | [[Datei:01-Goldener Winkel.svg.png|mini|123x123px|Goldener Winkel]] |
| − | + | Man betrachtet einen Kreis und teilt ihn in 2 Segmente, so dass die Teilumfänge a und b im goldenen Schnitt stehen. Dabei ergibt sich der Goldene Winkel indem man den Vollwinkel im goldenen Schnitt teilt: <math>\frac{2 \pi}{\Phi} \approx 222,5°</math>. Üblicherweise wird allerdings nicht der überstumpfe Winkel, sondern seine Ergänzung zum Vollkreis als Goldener Winkel bezeichnet: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <math>\Psi = 2\pi - \frac{2 \pi}{\Phi} \approx 137,5° </math>.<ref>Spiralen, Winkel und die "göttliche Proportion" - scinexx.de</ref> | |
| + | [[Datei:Goldener Schnitt Blattstand.png|mini|124x124px|Blattstand]] | ||
| − | + | ==== Goldener Winkel in der Natur ==== | |
| − | + | Interessant ist das Vorkommen des Goldenen Winkels in der Natur. Ein Beispiel sind die Kerne einer Sonnenblume. Diese sind angeordnet in rechts- und linksdrehenden Spiralen mit der Anzahl zweier aufeinanderfolgenden Fibonacci Zahlen. Außerdem ergeben sich bei der Sonnenblume die vorher aufgezeigten Spiralen durch die Umkreisung eines Strahls um einen Punkt im Goldenen Winkel. <ref>http://summa.stiftungrechnen.de/der-goldene-schnitt-und-die-schoenheit/ | |
| − | + | </ref><ref>http://www.3d-meier.de/tut22/Sonne/Seite1.html#:~:text=In%20der%20Sonnenblume%20sind%20die%20Kerne%20in%20Spiralen%20angeordnet.&text=Die%20Anordnung%20der%20Kerne%20in,sich%20vom%20Goldenen%20Schnitt%20ableitet.</ref> | |
| − | |||
| − | |||
| − | |||
| + | Bei Pflanzen ist die Anordnung von Blättern entlang ihres Stängels oft im Goldenen Winkel. Die Blätter wachsen spiralförmig um ihren Stängel und haben zu ihrem Nachbarn den Goldenen Winkel. Dadurch nehmen alle Blätter unterschiedliche Positionen um den Pflanzenholm ein, was besonders bei der Fotosynthese eine wichtige Rolle spielt. <ref>https://opus.ostfalia.de/frontdoor/deliver/index/docId/432/file/Schroth_2017_Goldener_Schnitt.pdf</ref> | ||
=== Pentagramm === | === Pentagramm === | ||
| − | Zuerst nimmt man ein regelmäßiges Fünfeck und zeichnet die | + | [[Datei:Pentagramm .jpg|alternativtext=|mini|167x167px|Pentagramm]] |
| + | Zuerst nimmt man ein regelmäßiges Fünfeck und zeichnet die Diagonalen ein. Die Diagonalen formen einen Stern mit fünf Zacken. Jedes gleichschenklige Dreieck, was sich im Pentagon bildet, ist ein goldenes Dreieck. Die Diagonalen teilen die Seiten im Goldenen Schnitt. Jede Sternspitze hat einen Winkel von 36°. | ||
<ref>https://christianrohrbach.net/wp-content/uploads/42-Goldener-Schnitt-Pentagramm.pdf</ref> | <ref>https://christianrohrbach.net/wp-content/uploads/42-Goldener-Schnitt-Pentagramm.pdf</ref> | ||
| − | == | + | ==== Vorkommen des Pentagramms ==== |
| − | Die | + | Das Pentagramm, auch Drudenfuß genannt, war das Zeichen der Pythagoräer und galt als magisches Zeichen. Die Streckenverhältnisse, die im Goldenen Schnitt stehen, sind inkommensurabel. Das bedeutet, dass die Strecken irrationale Längen haben und nur durch Zirkel und Lineal genau konstruiert werden können. <ref>F:\SCHULE\MA\AUFGABEN\09\pentagra.9p (herder-oberschule.de)</ref> |
| − | + | Eine Frage die aufgeworfen wird ist, ob das Pentagramm seit je her eine magische Wirkung nachgesagt wird, weil es durch die vielfache Verwendung des Goldenen Schnittes eine besondere oder besonders harmonische Wirkung hat. <ref>F:\SCHULE\MA\AUFGABEN\09\pentagra.9p (herder-oberschule.de)</ref> | |
| + | |||
| + | == Zusammenhang mit der [[Fibonacci Folge|Fibonacci-Folge]] == | ||
| + | Durch die Quotienten zweier aufeinanderfolgenden [[Fibonacci Folge|Fibonacci-Zahlen]] wird der Goldene Schnitt angenähert. | ||
| + | {| class="wikitable" | ||
| + | !<math>f_n</math> | ||
| + | !<math>f_{n+1}</math> | ||
| + | !<math>\frac{f_{n+1}}{f_n}</math> | ||
| + | |- | ||
| + | |<small><math>1</math></small> | ||
| + | |<small><math>1</math></small> | ||
| + | |<small><math>= 1</math></small> | ||
| + | |- | ||
| + | |<small><math>1</math></small> | ||
| + | |<small><math>2</math></small> | ||
| + | |<small><math>= 2</math></small> | ||
| + | |- | ||
| + | |<small><math>2</math></small> | ||
| + | |<small><math>3</math></small> | ||
| + | |<small><math>= 1,5</math></small> | ||
| + | |- | ||
| + | |<small><math>3</math></small> | ||
| + | |<small><math>5</math></small> | ||
| + | |<small><math>\approx 1,667 </math></small> | ||
| + | |- | ||
| + | |<small><math>5</math></small> | ||
| + | |<small><math>8</math></small> | ||
| + | |<small><math>= 1,6</math></small> | ||
| + | |- | ||
| + | |<small><math>8</math></small> | ||
| + | |<small><math>13</math></small> | ||
| + | |<small><math>= 1,625</math></small> | ||
| + | |- | ||
| + | |<small><math>13</math></small> | ||
| + | |<small><math>21</math></small> | ||
| + | |<small><math>\approx 1,6154 </math></small> | ||
| + | |- | ||
| + | |<small><math>21</math></small> | ||
| + | |<small><math>34</math></small> | ||
| + | |<small><math> \approx 1,619 </math></small> | ||
| + | |- | ||
| + | |<small><math>34</math></small> | ||
| + | |<small><math>55</math></small> | ||
| + | |<small><math> \approx 1,6176 </math></small> | ||
| + | |} | ||
== Der Goldener Schnitt in der Architektur == | == Der Goldener Schnitt in der Architektur == | ||
| Zeile 237: | Zeile 283: | ||
=== Leipziger Rathaus === | === Leipziger Rathaus === | ||
| − | Beim Bau des alten Leipziger Rathauses ließ der Architekt Hieronymus Lotter den Turmeingang und Turm so positionieren, dass er die Vorderfront des Gebäudes im Verhältnis des | + | Beim Bau des alten Leipziger Rathauses ließ der Architekt Hieronymus Lotter den Turmeingang und Turm so positionieren, dass er die Vorderfront des Gebäudes im Verhältnis des Goldenen Schnitts teilte. Kunst und Architektur wurden zu dieser Zeit geprägt von den Merkmalen der Renaissance, wie in diesem Fall mathematische Klarheit und Schönheit. <ref>https://www.planet-wissen.de/natur/forschung/mathematik/pwiedergoldeneschnitt100.html</ref> Das alte Rathaus erhielt dadurch die bis heute erkennbare asymmetrische Fassade die seitdem ein Wahrzeichen der Stadt ist.[[Datei:Petersdom Goldener Schnitt.png|mini|Petersdom mit mehreren goldenen Schnitten|alternativtext=|links]] |
| − | === | + | === Petersdom === |
| + | [[Datei:(Cheops) Pyramide.png|mini|200x200px|Pyramide mit eingezeichneten Längen|alternativtext=]]Da der Goldene Schnitt oft auch als "proportiona divina" (göttliches Maß) bezeichnet wird, ist er auch in vielen sakralen Bauten wiederzuentdecken, so auch in der größten päpstlichen Basilika der Welt: dem Petersdom in Rom. | ||
| − | === | + | === Cheops-Pyramide === |
| − | + | Die Cheopspyramide ist so konstruiert, dass die Höhe d eines Seitendreiecks zur halben Grundseitenlänge s/2 im Verhältnis des Goldenen Schnitts steht. Nach heutigem Wissen betrugen die Maße der Cheops-Pyramide vor Verwitterung etc. 146,5 Meter in der Höhe und 230,36 Meter Seitenlänge. Allerdings ist davon auszugehen, dass den Ägyptern der Goldenen Schnitt noch nicht bekannt war und sie die Pyramide nur nach reinen Ästhetik-Aspekten konstruierten. Zudem gab es bautechnische Limitierungen die eine steilere Steigung nicht erlaubten.<ref>''Professor Bernd Thaller „Goldene Verhältnisse: [http://www.oemg.ac.at/DK/Didaktikhefte/2011%20Band%2044/VortragThaller.pdf Das Geheimnis der großen Pyramide“]''</ref> Der Goldenen Schnitt ist hierbei dennoch wie folgt aufzufinden: <blockquote> | |
| − | + | <center><math> \frac{\text{Höhe des Seitendreiecks}}{\text{halbe Seitenlänge}} = \frac{\text{186,356 m}}{\text{115,18 m}} = 1,617957... \approx \Phi \\\\ </math></center> | |
| − | + | </blockquote> | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | ||
| − | |||
| − | |||
== Der Goldene Schnitt in der Kunst == | == Der Goldene Schnitt in der Kunst == | ||
[[Datei:Goldener Schnitt Fechner.jpg|mini|336x336px|Fechner Methode der Wahl]] | [[Datei:Goldener Schnitt Fechner.jpg|mini|336x336px|Fechner Methode der Wahl]] | ||
| − | In der Kunst wird der Goldene Schnitt | + | In der Kunst wird der Goldene Schnitt verwendet, um eine harmonische und schöne Wirkung zu erzielen. Es gibt viele Möglichkeiten den Goldenen Schnitt in der Kunst zu verwenden, ob nun die Goldenen Figuren oder den Goldenen Schnitt als Verhältnis der Proportionen. Meistens wird es mit dem Ziel der angeblichen Wirkungen verwendet. Auch wenn einige Studien zu der angeblichen Schönheit des Goldenen Schnittes existieren gibt es auch viele Zweifel daran. <ref>Der goldene Schnitt in der Kunst (goldener-schnitt.info)</ref> |
=== Empfinden des Goldenen Schnitts === | === Empfinden des Goldenen Schnitts === | ||
| − | Fechner hat mithilfe dreier verschiedener Methoden herauszufinden gesucht, ob der Goldene Schnitt tatsächlich bevorzugt wird. Diese Methoden waren die der Wahl, der Herstellung und der Verwendung. <ref>Fechner, Gustav, Zur experimentalen Ästhetik, Hirzel, Leipzig, 1871, Seite 50</ref> Bei der Methode der Wahl legte er den Probanden weiße Rechtecke vor und tatsächlich hat sich eine Bevorzugung jener Rechtecke herausgestellt die als Seitenverhältnis annähernd den Goldenen Schnitt haben. <ref>Schoot, Albert van der, Die Geschichte des Goldenen Schnitts, Aufstieg und Fall der göttlichen Proportion, Frommann-Holzboog, Stuttgart, 2005, Seite 215-225</ref> | + | Fechner hat mithilfe dreier verschiedener Methoden herauszufinden gesucht, ob der Goldene Schnitt tatsächlich bevorzugt wird. Diese Methoden waren die der Wahl, der Herstellung und der Verwendung. <ref>Fechner, Gustav, Zur experimentalen Ästhetik, Hirzel, Leipzig, 1871, Seite 50</ref> Bei der Methode der Wahl legte er den Probanden weiße Rechtecke vor und tatsächlich hat sich eine Bevorzugung jener Rechtecke herausgestellt die als Seitenverhältnis annähernd den Goldenen Schnitt haben. Die Methode der Verwendung besteht aus der Vermessung im Alltag genutzter Rechtecke. Dazu gehören zum Beispiel Spielkarten und Fenster. Auch hier hat sich ,laut Fechner, eine häufige Verwendung des Goldenen Schnittes rausgestellt. <ref>Schoot, Albert van der, Die Geschichte des Goldenen Schnitts, Aufstieg und Fall der göttlichen Proportion, Frommann-Holzboog, Stuttgart, 2005, Seite 215-225</ref> |
| + | |||
| + | === Berühmte Künstler und Kunstwerke === | ||
| + | [[Datei:Vitruvianischer Mensch.jpg|mini|172x172px|Vitruvianischer Mensch]] | ||
| + | Leonardo da Vinci gilt als einer der bekanntesten Künstler, bei dessen Kunstwerken der Goldene Schnitt zu erkennen ist. Der Vitruvianische Mensch gilt als Mensch mit optimalen Proportionen und diese Proportionen sind im Goldenen Schnitt. Auch bei der Mona Lisa ist vor allem die Verwendung der Goldenen Dreiecke zur Bildkonstruktion deutlich. <ref>https://www.lernhelfer.de/schuelerlexikon/kunst/artikel/proportion-und-goldener-schnitt</ref> | ||
| + | |||
| + | Auch bei anderen Künstlern wie Raffael und Dürer ist die Verwendung des Goldenen Schnittes auffällig. So zum Beispiel beim Triumph der Galatea, der Sixtinischen Madonna oder das Selbstbildnis von Dürer. <ref>https://www.lernhelfer.de/schuelerlexikon/kunst/artikel/proportion-und-goldener-schnitt</ref> Der französische Maler Paul Sérusier ist einer der wenigen, bei denen bekannt ist, dass er den Goldenen Schnitt bewusst eingesetzt hat. Bei vielen anderen, wie George Seurat oder Juan Gris, wird vermutet, dass der Goldene Schnitt unbewusst, wegen seiner umstrittenen harmonischen Wirkung genutzt wurde. <ref>https://goldener-schnitt.info/#der_goldene_schnitt_in_der_kunst</ref> | ||
== Quellen == | == Quellen == | ||
<references /> | <references /> | ||
| + | |||
| + | == Autoren == | ||
| + | Ines Christa, Konrad Kockler, Sebastian Splitthoff, Dennis Straub | ||
Aktuelle Version vom 12. April 2021, 13:34 Uhr
Der "Goldene Schnitt" bezeichnet allgemein ein spezielles Teilungsverhältnis einer Strecke.
Die Besonderheit dieses Verhältnisses besteht darin, die Gesamtstrecke in zwei Teile aufzuteilen, wobei die Gesamtstrecke dasselbe Teilungsverhältnis zur größeren Teilstrecke aufweist, wie auch die größere Teilstrecke (Major) zur kleineren Teilstrecke (Minor).
Den Quotient der Strecken nennt man die Goldene Zahl [math]\Phi[/math].
Herleitung des Goldenen Schnitts
Die obige Definition lässt sich algebraisch ausdrücken und wie folgt eindeutig lösen, wobei a (Major) und b (Minor) die Teilstrecken und a+b die Gesamtstrecke ist.
- [math] \Phi = \frac{a}{b} \overset{!}{=} \frac{a+b}{a} = 1+\frac{b}{a} = 1 + \frac{1}{\Phi}\\\\ [/math]
- [math] \Leftrightarrow \Phi^{2} = \Phi + 1 \\\\ [/math]
- [math] \Leftrightarrow 0 = \Phi^{2} - \Phi - 1 \\\\ [/math]
- [math] \Rightarrow \Phi_{1} = \frac{1+\sqrt[]{5}}{2} = \Phi \approx 1,618\\ [/math]
- [math] \Rightarrow \Phi_{2} = \frac{1-\sqrt[]{5}}{2} = \varphi \approx 0,618 [/math]
Wir nennen [math] \Phi [/math] die Goldene Zahl bzw. den Goldenen Schnitt, für den gilt:
- [math] \frac{1}{\Phi} = \Phi - 1 = \varphi[/math]
[math]\Phi[/math] als "irrationalste" Zahl
Allgemein gibt es keine irrationale Zahl die "irrationaler" als eine andere irrationale Zahl ist. [math]\Phi[/math] lässt sich nur sehr "langsam" durch rationale Zahlen annähern, daher die meist scherzhafte Aussage [math]\Phi[/math] sei die "irrationalste" Zahl.
Kettenbruchdarstellung
Um die Annäherung durch rationale Zahlen vorzunehmen, stellt man die Zahl als unendlichen Kettenbruch dar und bricht diesen an einer Stelle ab. Je später man abbricht, desto genauer die Annäherung.
[math] \Phi = 1 + \frac{1}{\Phi} = 1 + \frac{1}{1 + \frac{1}{\Phi}} = 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{\Phi}}} = 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{\Phi}}}} \quad ... [/math]
Wir sehen nun, dass der Kettenbruch von [math]\Phi[/math] nur Einsen als Elemente enthält, woraus sich wiederum folgern lässt, dass der Nenner der Näherung durch rationale Zahlen so langsam wie nur möglich wächst und sich somit eine möglichst genaue Approximation nur schlecht durchzuführen ist.
Daher die Aussage [math]\Phi[/math] sei die irrationalste nur mögliche Zahl.
Interessant hierbei ist, dass der Näherungsbruch immer aus zwei aufeinanderfolgenden Fibonacci-Zahlen besteht.
| Abbruch nach n Elementen | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | [math]\vdots[/math] | Die rekursive Bildungsformel lautet: [math] \frac{p_{n}}{q_{n}} = \frac{p_{n-1} + q_{n-1}}{p_{n-1}} [/math] |
|---|---|---|---|---|---|---|---|---|---|---|
| Näherungswert | 2 | [math] \frac{3}{2} [/math] | [math] \frac{5}{3} [/math] | [math] \frac{8}{5} [/math] | [math] \frac{13}{8} [/math] | [math] \frac{21}{13} [/math] | [math] \frac{34}{21} [/math] | [math] \frac{55}{34} [/math] | ||
| Abweichung von [math] \Phi [/math] in % | 23,6 | 7,3 | 3 | 1,1 | 0,43 | 0,16 | 0,062 | 0,024 |
Kettenwurzeldarstellung
Alternativ lässt sich [math]\Phi[/math] auch durch eine unendliche Kettenwurzel nähern, dies folgt aus [math]\Phi^{2} = \Phi + 1[/math]
- [math] \Phi = \sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+...}}}} [/math]
Geometrische Konstruktion von [math]\Phi[/math]
Unterschieden wird die geometrische Konstruktion in innere und äußere Teilung. Die innere Teilung teilt eine gegebene Strecke im goldenen Schnitt, wohingegen die äußere Teilung zu einer gegebenen Strecke eine weitere außerhalb liegende Strecke konstruiert, sodass die Beiden im goldenen Verhältnis zueinander stehen.
Innere Teilung
| "klassische Methode" zur inneren Teilung:
Gegeben sei eine beliebige Länge [math] \overline{AB}[/math]. Die Strecke [math] \overline{BC}[/math] steht senkrecht zu [math] \overline{AB}[/math] im Punkt B und hat die Länge [math] \frac{\overline{AB}}{2}[/math]. Der Kreis um C mit Radius [math] \overline{BC}[/math] schneidet die Strecke [math] \overline{AC}[/math] im Punkt D. Der Kreis um A mit Radius [math] \overline{AD}[/math] teilt die Strecke [math] \overline{AB}[/math] im Verhältnis des Goldenen Schnitts. Beweis: | |
| Methode nach Euklid:
Gegeben sei eine beliebige Länge [math] \overline{AB}[/math]. Die Strecke [math] \overline{BC}[/math] steht senkrecht zu [math] \overline{AB}[/math] im Punkt B und hat die Länge [math] \frac{\overline{AB}}{2}[/math]. Der Kreis um C mit Radius [math] \overline{AC}[/math] ergibt Punkt D, welche auf der Verlängerung der Strecke [math] \overline{BC}[/math] liegt. Der Kreis um B mit Radius [math] \overline{BD}[/math] teilt die Strecke [math] \overline{AB}[/math] im Verhältnis des Goldenen Schnitts. |
Äußere Teilung
| "klassische Methode" zur äußeren Teilung:
Gegeben ist eine Strecke [math] \overline{AB}[/math]. Die Strecke [math] \overline{BC}[/math] hat die gleiche Länge wie [math] \overline{AB}[/math] und steht senkrecht auf Punkt B. Der Punkt H teilt die Strecke [math] \overline{AB}[/math] in der Hälfte. Der Kreis um Punkt H mit Radius [math] \overline{HC}[/math] schneidet die Verlängerung von [math] \overline{AB}[/math] im Punkt M. Punkt B teilt nun die Strecke [math] \overline{AM}[/math] im goldenen Schnitt. Beweis: | |
| Methode nach George Odom:
Gegeben sei ein gleichseitiges Dreieck mit Umkreis. Teilt man nun zwei Seiten des Dreiecks in der Mitte und verbindet die Punkte (A, B) so ergibt die Verlängerung von [math] \overline{AB}[/math] einen Schnittpunkt S mit dem Umkreis. Punkt B teilt nun die Strecke [math] \overline{AS}[/math] im goldenen Schnitt. |
Goldene Geometrie
Goldenes Rechteck
Unter einem Goldenen Rechteck verstehen wir das Rechteck mit dem Seitenverhältnis des Goldenen Schnittes. [2]Das bedeutet die Seiten a und b stehen im Verhältnis [math] \frac{a}{b} = \frac{a+b}{a} \\ [/math].
Konstruiert wird das Goldene Rechtecks durch eine abgewandelte Form der äußeren Konstruktion. Gegeben haben wir eine Strecke a, aus welcher wir ein Quadrat konstruieren. Wie oben beschrieben wird zur Teilstrecke a die Teilstrecke b im Goldenen Schnitt konstruiert. Nun haben wir das Quadrat mit der Seitenlänge a und die Teilstrecke b, was wir nun zu einem Goldenen Rechteck ergänzen können. [3]
Eine Besonderheit des Goldenen Rechtecks ist, dass man immer ein Goldenes Rechteck erhält wenn man von einem Goldenen Rechteck ein größtmögliches Quadrat abschneidet. In dem Bild gibt also das kleinere rote Rechteckt wieder ein Goldenes Rechteck. Dies kann beliebig oft wiederholt werden. [4]
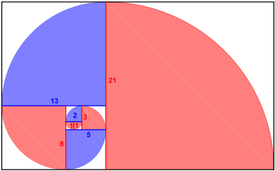
Goldene Spirale
Wenn wir ein Goldenes Rechteck in ein größtmögliches Quadrat und ein kleineres Goldenes Rechteck einteilen und dies bei dem kleineren wiederholen und immer bei dem kleineren Rechteck so machen, entsteht eine endlose Folge. Zeichnen wir jetzt ,in die Quadrate, in geeigneter Weise Viertelkreise ein, entsteht eine Spirale, die eine gute Approximation der logarithmischen Spirale ist. Der Mittelpunkt der Spirale liegt auf dem Schnittpunkt der Diagonalen des ersten und des zweiten Goldenen Rechtecks. [5] Besonders ist auch der Zusammenhang mit der Fibonacci-Folge, da die Radien der Kreissektoren genau der Folge entspricht. [6]
Goldene Dreiecke
Es gibt zwei unterschiedliche Arten des Goldenes Dreiecks, ein spitzes (erster Art) und ein stumpfes (zweiter Art). Beides sind gleichschenklige Dreiecke, bei denen ein Schenkel zur Grundseite im Goldenen Schnitt steht. [7]
Beim Goldenen Dreieck erster Art bilden die Schenkel die Majoren, also die längere Teilstrecke, und die Grundseite ist der Minor. Die beiden Winkel die an die Grundseite grenzen haben 72° und der dritte 36°. Das Goldene Dreieck zweiter Art hat zwei Minoren, die Schenkel, und die Basiswinkel haben jeweils 36° während der dritte Winkel 108° hat. [8]
Herleitung: Mit [math]\frac{k}{a}=\Phi[/math] können wir auch die Winkel im Dreieck berechnen:
[math] \begin{align*} \cos(\alpha) &= \frac{\frac{a}{2}}{k} = \frac{a}{2k} = \frac{1}{2\Phi}\\ \Leftrightarrow \alpha &= 72°\\ \end{align*} [/math]
Damit bekommen wir:
[math] \begin{align*} 180° - 90° - 72° = 18° \rightarrow \beta &= 36° \\ \end{align*} [/math]
Im stumpfwinkligen Dreieck bekommen wir noch einen Winkel: [math]180° - 2 \cdot 36° = 108°[/math]
Insbesondere können wir vom Goldenen Dreieck erster Art ein größtmögliches Goldenes Dreieck zweiter Art abschneiden und zurück bleibt ein Goldenes Dreieck erster Art. [9]
Goldener Winkel
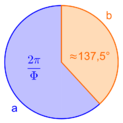
Man betrachtet einen Kreis und teilt ihn in 2 Segmente, so dass die Teilumfänge a und b im goldenen Schnitt stehen. Dabei ergibt sich der Goldene Winkel indem man den Vollwinkel im goldenen Schnitt teilt: [math]\frac{2 \pi}{\Phi} \approx 222,5°[/math]. Üblicherweise wird allerdings nicht der überstumpfe Winkel, sondern seine Ergänzung zum Vollkreis als Goldener Winkel bezeichnet:
[math]\Psi = 2\pi - \frac{2 \pi}{\Phi} \approx 137,5° [/math].[10]
Goldener Winkel in der Natur
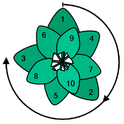
Interessant ist das Vorkommen des Goldenen Winkels in der Natur. Ein Beispiel sind die Kerne einer Sonnenblume. Diese sind angeordnet in rechts- und linksdrehenden Spiralen mit der Anzahl zweier aufeinanderfolgenden Fibonacci Zahlen. Außerdem ergeben sich bei der Sonnenblume die vorher aufgezeigten Spiralen durch die Umkreisung eines Strahls um einen Punkt im Goldenen Winkel. [11][12]
Bei Pflanzen ist die Anordnung von Blättern entlang ihres Stängels oft im Goldenen Winkel. Die Blätter wachsen spiralförmig um ihren Stängel und haben zu ihrem Nachbarn den Goldenen Winkel. Dadurch nehmen alle Blätter unterschiedliche Positionen um den Pflanzenholm ein, was besonders bei der Fotosynthese eine wichtige Rolle spielt. [13]
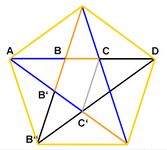
Pentagramm
Zuerst nimmt man ein regelmäßiges Fünfeck und zeichnet die Diagonalen ein. Die Diagonalen formen einen Stern mit fünf Zacken. Jedes gleichschenklige Dreieck, was sich im Pentagon bildet, ist ein goldenes Dreieck. Die Diagonalen teilen die Seiten im Goldenen Schnitt. Jede Sternspitze hat einen Winkel von 36°. [14]
Vorkommen des Pentagramms
Das Pentagramm, auch Drudenfuß genannt, war das Zeichen der Pythagoräer und galt als magisches Zeichen. Die Streckenverhältnisse, die im Goldenen Schnitt stehen, sind inkommensurabel. Das bedeutet, dass die Strecken irrationale Längen haben und nur durch Zirkel und Lineal genau konstruiert werden können. [15]
Eine Frage die aufgeworfen wird ist, ob das Pentagramm seit je her eine magische Wirkung nachgesagt wird, weil es durch die vielfache Verwendung des Goldenen Schnittes eine besondere oder besonders harmonische Wirkung hat. [16]
Zusammenhang mit der Fibonacci-Folge
Durch die Quotienten zweier aufeinanderfolgenden Fibonacci-Zahlen wird der Goldene Schnitt angenähert.
| [math]f_n[/math] | [math]f_{n+1}[/math] | [math]\frac{f_{n+1}}{f_n}[/math] |
|---|---|---|
| [math]1[/math] | [math]1[/math] | [math]= 1[/math] |
| [math]1[/math] | [math]2[/math] | [math]= 2[/math] |
| [math]2[/math] | [math]3[/math] | [math]= 1,5[/math] |
| [math]3[/math] | [math]5[/math] | [math]\approx 1,667 [/math] |
| [math]5[/math] | [math]8[/math] | [math]= 1,6[/math] |
| [math]8[/math] | [math]13[/math] | [math]= 1,625[/math] |
| [math]13[/math] | [math]21[/math] | [math]\approx 1,6154 [/math] |
| [math]21[/math] | [math]34[/math] | [math] \approx 1,619 [/math] |
| [math]34[/math] | [math]55[/math] | [math] \approx 1,6176 [/math] |
Der Goldener Schnitt in der Architektur
Leipziger Rathaus
Beim Bau des alten Leipziger Rathauses ließ der Architekt Hieronymus Lotter den Turmeingang und Turm so positionieren, dass er die Vorderfront des Gebäudes im Verhältnis des Goldenen Schnitts teilte. Kunst und Architektur wurden zu dieser Zeit geprägt von den Merkmalen der Renaissance, wie in diesem Fall mathematische Klarheit und Schönheit. [17] Das alte Rathaus erhielt dadurch die bis heute erkennbare asymmetrische Fassade die seitdem ein Wahrzeichen der Stadt ist.
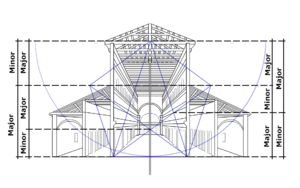
Petersdom
Da der Goldene Schnitt oft auch als "proportiona divina" (göttliches Maß) bezeichnet wird, ist er auch in vielen sakralen Bauten wiederzuentdecken, so auch in der größten päpstlichen Basilika der Welt: dem Petersdom in Rom.
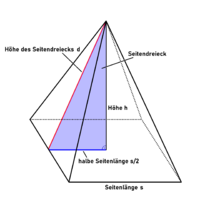
Cheops-Pyramide
Die Cheopspyramide ist so konstruiert, dass die Höhe d eines Seitendreiecks zur halben Grundseitenlänge s/2 im Verhältnis des Goldenen Schnitts steht. Nach heutigem Wissen betrugen die Maße der Cheops-Pyramide vor Verwitterung etc. 146,5 Meter in der Höhe und 230,36 Meter Seitenlänge. Allerdings ist davon auszugehen, dass den Ägyptern der Goldenen Schnitt noch nicht bekannt war und sie die Pyramide nur nach reinen Ästhetik-Aspekten konstruierten. Zudem gab es bautechnische Limitierungen die eine steilere Steigung nicht erlaubten.[18] Der Goldenen Schnitt ist hierbei dennoch wie folgt aufzufinden:
[math] \frac{\text{Höhe des Seitendreiecks}}{\text{halbe Seitenlänge}} = \frac{\text{186,356 m}}{\text{115,18 m}} = 1,617957... \approx \Phi \\\\ [/math]
Der Goldene Schnitt in der Kunst
In der Kunst wird der Goldene Schnitt verwendet, um eine harmonische und schöne Wirkung zu erzielen. Es gibt viele Möglichkeiten den Goldenen Schnitt in der Kunst zu verwenden, ob nun die Goldenen Figuren oder den Goldenen Schnitt als Verhältnis der Proportionen. Meistens wird es mit dem Ziel der angeblichen Wirkungen verwendet. Auch wenn einige Studien zu der angeblichen Schönheit des Goldenen Schnittes existieren gibt es auch viele Zweifel daran. [19]
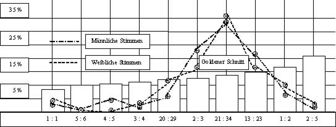
Empfinden des Goldenen Schnitts
Fechner hat mithilfe dreier verschiedener Methoden herauszufinden gesucht, ob der Goldene Schnitt tatsächlich bevorzugt wird. Diese Methoden waren die der Wahl, der Herstellung und der Verwendung. [20] Bei der Methode der Wahl legte er den Probanden weiße Rechtecke vor und tatsächlich hat sich eine Bevorzugung jener Rechtecke herausgestellt die als Seitenverhältnis annähernd den Goldenen Schnitt haben. Die Methode der Verwendung besteht aus der Vermessung im Alltag genutzter Rechtecke. Dazu gehören zum Beispiel Spielkarten und Fenster. Auch hier hat sich ,laut Fechner, eine häufige Verwendung des Goldenen Schnittes rausgestellt. [21]
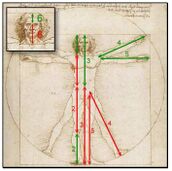
Berühmte Künstler und Kunstwerke
Leonardo da Vinci gilt als einer der bekanntesten Künstler, bei dessen Kunstwerken der Goldene Schnitt zu erkennen ist. Der Vitruvianische Mensch gilt als Mensch mit optimalen Proportionen und diese Proportionen sind im Goldenen Schnitt. Auch bei der Mona Lisa ist vor allem die Verwendung der Goldenen Dreiecke zur Bildkonstruktion deutlich. [22]
Auch bei anderen Künstlern wie Raffael und Dürer ist die Verwendung des Goldenen Schnittes auffällig. So zum Beispiel beim Triumph der Galatea, der Sixtinischen Madonna oder das Selbstbildnis von Dürer. [23] Der französische Maler Paul Sérusier ist einer der wenigen, bei denen bekannt ist, dass er den Goldenen Schnitt bewusst eingesetzt hat. Bei vielen anderen, wie George Seurat oder Juan Gris, wird vermutet, dass der Goldene Schnitt unbewusst, wegen seiner umstrittenen harmonischen Wirkung genutzt wurde. [24]
Quellen
- ↑ Funfacts Vorlesung; Universität Heidelberg; Wintersemester 20/21
- ↑ Walser, Hans, Der Goldene Schnitt, Eagle Einblicke, Leipzig, 2009, 5.Auflage, Seite 39
- ↑ Walser, Hans, Der Goldene Schnitt, Eagle Einblicke, Leipzig, 2009, 5.Auflage, Seite 39
- ↑ Walser, Hans, Der Goldene Schnitt, Eagle Einblicke, Leipzig, 2009, 5.Auflage, Seite 40
- ↑ Beutelspacher, Albrecht, Petri, Bernhard, Der Goldene Schnitt, B.I. Wissenschaftsverlag, 1989, Seite 57
- ↑ Ausarbeitung Goldene Spirale (ph-freiburg.de)
- ↑ Walser, Hans, Der Goldene Schnitt, Eagle Einblicke, Leipzig, 2009, 5.Auflage, Seite 51
- ↑ Walser, Hans, Der Goldene Schnitt, Eagle Einblicke, Leipzig, 2009, 5.Auflage, Seite 51
- ↑ Walser, Hans, Der Goldene Schnitt, Eagle Einblicke, Leipzig, 2009, 5.Auflage, Seite 51
- ↑ Spiralen, Winkel und die "göttliche Proportion" - scinexx.de
- ↑ http://summa.stiftungrechnen.de/der-goldene-schnitt-und-die-schoenheit/
- ↑ http://www.3d-meier.de/tut22/Sonne/Seite1.html#:~:text=In%20der%20Sonnenblume%20sind%20die%20Kerne%20in%20Spiralen%20angeordnet.&text=Die%20Anordnung%20der%20Kerne%20in,sich%20vom%20Goldenen%20Schnitt%20ableitet.
- ↑ https://opus.ostfalia.de/frontdoor/deliver/index/docId/432/file/Schroth_2017_Goldener_Schnitt.pdf
- ↑ https://christianrohrbach.net/wp-content/uploads/42-Goldener-Schnitt-Pentagramm.pdf
- ↑ F:\SCHULE\MA\AUFGABEN\09\pentagra.9p (herder-oberschule.de)
- ↑ F:\SCHULE\MA\AUFGABEN\09\pentagra.9p (herder-oberschule.de)
- ↑ https://www.planet-wissen.de/natur/forschung/mathematik/pwiedergoldeneschnitt100.html
- ↑ Professor Bernd Thaller „Goldene Verhältnisse: Das Geheimnis der großen Pyramide“
- ↑ Der goldene Schnitt in der Kunst (goldener-schnitt.info)
- ↑ Fechner, Gustav, Zur experimentalen Ästhetik, Hirzel, Leipzig, 1871, Seite 50
- ↑ Schoot, Albert van der, Die Geschichte des Goldenen Schnitts, Aufstieg und Fall der göttlichen Proportion, Frommann-Holzboog, Stuttgart, 2005, Seite 215-225
- ↑ https://www.lernhelfer.de/schuelerlexikon/kunst/artikel/proportion-und-goldener-schnitt
- ↑ https://www.lernhelfer.de/schuelerlexikon/kunst/artikel/proportion-und-goldener-schnitt
- ↑ https://goldener-schnitt.info/#der_goldene_schnitt_in_der_kunst
Autoren
Ines Christa, Konrad Kockler, Sebastian Splitthoff, Dennis Straub