Museumswächterproblem: Unterschied zwischen den Versionen
LasseB (Diskussion | Beiträge) |
|||
| (10 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Das Museum ist wegen Corona geschlossen, deswegen werden keine | + | Das Museum ist wegen Corona geschlossen, deswegen werden keine Wächterinnen benötigt :-( |
| + | |||
| + | Bei diesem Problem geht es darum, dass ein Museumsdirektor sicherstellen möchte, dass jeder Punkt seines Museums überwacht wird. Dafür werden Museumswächterinnen an festen Stellen im Museum platziert, dürfen sich aber drehen. Nun lautet die Frage, wie viele Wächterinnen benötigt werden, um das Museum zu überwachen. | ||
== Museum Ritter == | == Museum Ritter == | ||
| − | [[Datei:Animation ritter.mp4|mini|200x200px|Hier sieht man sehr gut, dass | + | [[Datei:Animation ritter.mp4|mini|200x200px|Hier sieht man sehr gut, dass eine Wächterin an einer beliebigen Position ausreichend ist.]] |
| − | Zuerst | + | Zuerst betrachten wir das [https://www.museum-ritter.de/de/inhalt/home.html Museum Ritter], welches zum gleichnamigen Schokoladenhersteller gehört. Natürlich ist der Grundriss in unserer idealisierten Mathewelt perfekt quadratisch. Der Museumsdirektor möchte nun Museumswächterinnen einstellen und fragt sich, wie viele Leute er anstellen muss, wenn eine Wächterin sich zwar nicht frei im Raum bewegen, aber sich um ihre Achse drehen darf. Die Antwort auf die Frage ist trivial, es reicht, eine Wächterin irgendwo im Raum zu positionieren, wie relativ direkt aus der Definition der Konvexität folgt. Wie sieht es aber aus, wenn das Museum einen etwas komplizierteren Grundriss besitzt? |
== Satz == | == Satz == | ||
| − | Nun betrachten wir ein Museum mit einem beliebigen Grundriss, welcher allerdings komplexer ist als der Grundriss des Museum Ritter. Einzige Voraussetzung ist, dass sich alle Wände durch eine Gerade beschreiben lassen. | + | Nun betrachten wir ein Museum mit einem beliebigen Grundriss, welcher allerdings komplexer ist als der Grundriss des Museum Ritter. Einzige Voraussetzung ist, dass sich alle Wände durch eine Gerade beschreiben lassen. Nun möchte unser Museumsdirektor wieder Wächterinnen einstellen und fragt sich, wie viele er braucht, damit diese das komplette Museum im Blick haben. Auch hier gilt wieder, dass sich die Wächterinnen nicht hin und her bewegen, sondern auf ihren Plätzen bleiben und sich nur um ihre Achse drehen können. Dann benötigt man folgende Anzahl an Wächterinnen: <blockquote> |
| − | Für jedes Museum mit <math>n</math> Wänden reichen <math>\lfloor \frac{n}{3} \rfloor</math> | + | Für jedes Museum mit <math>n</math> Wänden reichen <math>\lfloor \frac{n}{3} \rfloor</math> Wächterinnen aus. |
</blockquote> | </blockquote> | ||
| + | Dabei bedeuten die sogenannten Gaußklammern <math>\lfloor\, \rfloor</math>, dass der Nachkommateil des Qoutienten <math> \frac{n}{3}</math>, abgeschnitten, dieser also auf die nächstkleinere ganze Zahl abgerundet wird. | ||
== Beweis nach Steve Fisk == | == Beweis nach Steve Fisk == | ||
| Zeile 15: | Zeile 18: | ||
=== Definition: Polygon=== | === Definition: Polygon=== | ||
| − | Ein Polygon ist ein Tupel <math>P= | + | Ein Polygon ist ein Tupel <math>P= \left(P_1,P_2,\dots,P_n \right)</math>, von n verschiedenen Punkten <math>P_i\ (\text{mit}\ 1\leq i\leq n,\ n\in\mathbb{N})</math>. Dabei heißen die <math>n</math> Punkte Eckpunkte des Polygons (man spricht auch von einem <math>n</math>-Eck) und die Strecken <math>\overline{P_iP_{i+1}}</math> für <math> (1\leq i\leq n-1)</math> und <math>\overline{P_1P_n}</math> zwischen den Eckpunkten werden als Kanten oder Seiten bezeichnet. |
Die Verbindungsstrecken zweier Punkte die keinen Kanten sind werden als Diagonalen bezeichnet.<br> | Die Verbindungsstrecken zweier Punkte die keinen Kanten sind werden als Diagonalen bezeichnet.<br> | ||
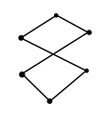
In unserem Fall betrachten wir nur planare Polygone, das heißt n-Ecke, welche in der Ebene liegen. Zusätzlich kann es sein, dass sich die Kanten nicht nur in den Eckpunkten schneiden, in diesem Fall spricht man von einem überschlagenen Polygon. | In unserem Fall betrachten wir nur planare Polygone, das heißt n-Ecke, welche in der Ebene liegen. Zusätzlich kann es sein, dass sich die Kanten nicht nur in den Eckpunkten schneiden, in diesem Fall spricht man von einem überschlagenen Polygon. | ||
| Zeile 25: | Zeile 28: | ||
</gallery> | </gallery> | ||
| − | === Definition: | + | === Definition: Triangulierung === |
Als Triangulation eines Polygons bezeichnen wir hier einen planaren Graph, welcher entsteht, wenn man die Innenfläche des Polygons durch Diagonalen, welche sich nicht schneiden, mit Dreiecken ausfüllt. | Als Triangulation eines Polygons bezeichnen wir hier einen planaren Graph, welcher entsteht, wenn man die Innenfläche des Polygons durch Diagonalen, welche sich nicht schneiden, mit Dreiecken ausfüllt. | ||
| − | Für konvexe | + | Für konvexe Polygone ist klar, dass eine Triangulation immer möglich ist |
| − | === Satz: Für alle | + | === Satz: Für alle planaren Polygone P existiert eine Triangulation === |
| − | ''Beweis:'' Wir zeigen nun per | + | ''Beweis:'' Wir zeigen nun per vollständiger Induktion die Aussage für allgemeine planare Polygone. Sei n die Zahl der Ecken. |
| − | '''IA:''' für <math>n=3</math> ist P ein Dreieck also schon trianguliert. | + | '''IA:''' für <math>n=3</math> ist <math>P</math> ein Dreieck also schon trianguliert. |
| − | '''IV:''' Der Satz gilt für alle Polygone mit weniger als n Ecken | + | '''IV:''' Der Satz gilt für alle Polygone mit weniger als <math>n</math> Ecken |
| − | '''IS:''' <math>n-1\rightarrow n</math> Wir suchen eine Diagonale, die P in zwei Polygone <math>P_1</math> und <math>P_2</math> teilt. Dazu nehmen wir eine Ecke <math>E_1</math> mit Innenwinkel kleiner als 180° (existiert immer) und verbinden die beiden zu <math>E_1</math> benachbarten Ecken <math>E_2</math> und <math>E_3</math>. Nun sind 2 Fälle möglich: | + | '''IS:''' <math>(n-1)\rightarrow n</math> Wir suchen eine Diagonale, die P in zwei Polygone <math>P_1</math> und <math>P_2</math> teilt. Dazu nehmen wir eine Ecke <math>E_1</math> mit Innenwinkel kleiner als 180° (existiert immer) und verbinden die beiden zu <math>E_1</math> benachbarten Ecken <math>E_2</math> und <math>E_3</math>. Nun sind 2 Fälle möglich: |
Fall 1: <math>\overline{E_2E_3}</math> ist vollständig in P enthalten. Dann ist mit dieser Diagonal das Polygon in zwei Polygone zerteilt mit jeweils weniger als n Ecken. Nach IV sind diese dann natürlich triangulierbar. Damit folgt die Behauptung auch für das gesamte Polygon. | Fall 1: <math>\overline{E_2E_3}</math> ist vollständig in P enthalten. Dann ist mit dieser Diagonal das Polygon in zwei Polygone zerteilt mit jeweils weniger als n Ecken. Nach IV sind diese dann natürlich triangulierbar. Damit folgt die Behauptung auch für das gesamte Polygon. | ||
| Zeile 58: | Zeile 61: | ||
===Satz: Jede Triangulation eines Polygons P ist 3-färbbar=== | ===Satz: Jede Triangulation eines Polygons P ist 3-färbbar=== | ||
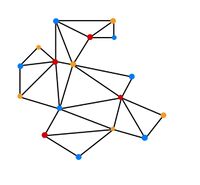
| − | [[Datei:Triangulierung2.jpg|alternativtext=|mini|200x200px|Das Polygon hat 17 Ecken, davon vier rote, 7 blaue und 6 gelbe. Wenn man nun je | + | [[Datei:Triangulierung2.jpg|alternativtext=|mini|200x200px|Das Polygon hat 17 Ecken, davon vier rote, 7 blaue und 6 gelbe. Wenn man nun je eine Wächterin in die roten Ecken stellt, reichen vier Wächterinnen aus. Dies entspricht unserer Erwartung, dass wir höchstens <math> \lfloor \frac{17}{3}\rfloor = 5 </math> Wächterinnen benötigen.]]'''Beweis:''' Wir zeigen die Aussage per vollständige Induktion. |
'''IA:''' Für <math>n=3</math> ist P ein Dreieck und somit die Aussage trivialerweise erfüllt. | '''IA:''' Für <math>n=3</math> ist P ein Dreieck und somit die Aussage trivialerweise erfüllt. | ||
| Zeile 67: | Zeile 70: | ||
Da diese das Polygon in zwei Polygone mit weniger als <math>n</math> Ecken teilt, lässt sich die Induktionsvoraussetzung anwenden, womit die Aussage auch für das zusammengesetze Polygon gilt (seien hierfür o. B. d. A. in beiden Polygonen die Farben von <math>E_1</math> und <math>E_2</math> gleich gewählt). | Da diese das Polygon in zwei Polygone mit weniger als <math>n</math> Ecken teilt, lässt sich die Induktionsvoraussetzung anwenden, womit die Aussage auch für das zusammengesetze Polygon gilt (seien hierfür o. B. d. A. in beiden Polygonen die Farben von <math>E_1</math> und <math>E_2</math> gleich gewählt). | ||
| − | === Finaler Beweis nach Fisk: === | + | === Finaler Beweis des Museumswächterproblems nach Fisk: === |
| − | Für ein Museum mit <math>n=3</math> Ecken ist die Anzahl der | + | Für ein Museum mit <math>n=3</math> Ecken ist die Anzahl der Wächterinnen klar. Für ein Museum mit <math>n>3</math> Ecken beschreiben wir den Grundriss als Polygon, wobei die Anzahl der Ecken derjenigen der Wände entspricht. Wir nutzen nun, dass jedes Polygon triangulierbar und jede Triangulation 3-färbbar ist, wir wählen hierfür o.B.d.A die Farben <span style="color:#FF0000"> rot</span>, <span style="color:#0000FF">blau</span> und <span style="color:#FFA500"> orange</span>. Mindestens eine dieser Farben muss damit maximal <math>\lfloor \frac{n}{3} \rfloor</math>-mal vertreten sein, wenn <math>n</math> die Gesamtzahl der Ecken bezeichnet. |
| − | In unserer Triangulierung besitzt jedes einzelne Dreieck nach Konstruktion eine rote, eine blaue und eine gelbe Ecke. Besetzt man also alle Ecken einer Farbe mit einer | + | In unserer Triangulierung besitzt jedes einzelne Dreieck nach Konstruktion eine rote, eine blaue und eine gelbe Ecke. Besetzt man also alle Ecken einer Farbe mit einer Museumswächterin, so lässt sich jedes Dreieck (Dreiecke sind konvex) und damit das gesamte Museum einsehen. Somit reichen in jedem Museum <math>\lfloor \frac{n}{3} \rfloor</math> Wächterinnen aus, um das gesamte Museum zu überblicken. |
== Beispielrechnung am Guggenheim-Museum Bilbao == | == Beispielrechnung am Guggenheim-Museum Bilbao == | ||
| − | Da er das Museum Ritter so gut mit | + | Da er das Museum Ritter so gut mit Wächterinnen ausgestattet hat, wurde der Direktor befördert und arbeitet nun im renommierten Guggenheim-Museum in Bilbao. Auch hier soll er wieder Wärterinnen anstellen und zwar wieder zu den gleichen Bedingungen wie zuvor. Sie werden also wieder in Ecken positioniert, in denen sie sich drehen, aber nicht ihren Posten verlassen dürfen. Dazu wird, wie in der Nebenstehenden Graphik gezeigt, der Grundriss des Museums trianguliert. Anschließend werden die Ecken wieder gefärbt und gezählt. Dabei ergibt sich eine Anzahl von 27 roten Ecken, 27 orange Ecken und 28 blauen Ecken, also bräuchte man 27 Wächterinnen. Um zu überprüfen, ob sich der Direktor nicht verzählt hat, wendet er noch den Satz des Museumswächterinnenproblems an. Dazu zählt er alle Wände und kommt auf eine Anzahl von insgesamt 85. Nun strengt er seine grauen Zellen an und errechnet damit, dass er höchstens <math> \lfloor \frac{82}{3} \rfloor =27 </math> Wächterinnen braucht. Dies stimmt mit seinen Erwartungen überein und er ist sehr glücklich. |
<gallery widths="250" heights="250"> | <gallery widths="250" heights="250"> | ||
| − | Datei:Guggenheim.jpg|Guggenheim-Museum in Bilbao | + | Datei:Guggenheim.jpg|Guggenheim-Museum in Bilbao<ref>Von "Foto Wolfgang Pehlemann", CC-by-sa V. 3.0, CC BY-SA 3.0 de, <<nowiki>https://commons.wikimedia.org/w/index.php?curid=77457392</nowiki>></ref> |
Datei:Animation.mp4|Triangulierung des Grundrisses des Mueseums | Datei:Animation.mp4|Triangulierung des Grundrisses des Mueseums | ||
Datei:Guggenheim bunte Ecken.jpg|Dreifärbung nach der Triangulation | Datei:Guggenheim bunte Ecken.jpg|Dreifärbung nach der Triangulation | ||
| Zeile 80: | Zeile 83: | ||
== Trivia == | == Trivia == | ||
| − | + | Nach ungenauen Berechnungen des Museumsdirektors wird er aus dem Guggenheim-Museum in Bilbao entlassen. So kehrt er ins Museum Ritter zurück. Voller Schreck entdeckt er, dass sich das Museum ja komplett verändert hat. Anstatt eines einfachen Quadrates ist er nun Leiter des realen Museum Ritter, welches im Inneren Wände hat. Zum Glück hat der Direktor in Bilbao genügend Erfahrung im Triangulieren gesammelt, weswegen es nun ein Leichtes für ihn ist, auch das Museum Ritter, mit dem neuen Grundriss, ideal mit Wächterinnen zu besetzen.<gallery widths="250" heights="250"> | |
| − | + | Datei:Waldenbuch-Museum-Ritter.jpg|Das reale Museum Ritter<ref>Quelle: Foto von "user:enslin", CC BY-SA 3.0 de, <<nowiki>http://creativecommons.org/licenses/by-sa/3.0/</nowiki>>, via Wikimedia Commons</ref> | |
| − | Nach ungenauen Berechnungen des Museumsdirektors wird er aus dem Guggenheim-Museum in Bilbao entlassen. So kehrt er ins Museum Ritter zurück. Voller Schreck entdeckt er, dass sich das Museum ja komplett verändert hat. Anstatt eines einfachen Quadrates ist er nun Leiter des realen | + | Datei:Animation Ritter Triangulierung.mp4|Triangulierung des realen Museum Ritter |
| + | </gallery> | ||
== Ausblick == | == Ausblick == | ||
| Zeile 101: | Zeile 105: | ||
* http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.67.8231&rep=rep1&type=pdf, Stand 25.03.2021 | * http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.67.8231&rep=rep1&type=pdf, Stand 25.03.2021 | ||
* Grundriss des Museums frei nach https://de.wikiarquitectura.com/geb%C3%A4ude/guggenheim-bilbao/, Stand 25.03.2021 | * Grundriss des Museums frei nach https://de.wikiarquitectura.com/geb%C3%A4ude/guggenheim-bilbao/, Stand 25.03.2021 | ||
| + | <references /> | ||
| + | |||
| + | == Autoren == | ||
| + | Julie Drhova, Joris Hoffmann, Hjalmar Brunßen, Lasse Bassermann | ||
Aktuelle Version vom 12. April 2021, 19:03 Uhr
Das Museum ist wegen Corona geschlossen, deswegen werden keine Wächterinnen benötigt :-(
Bei diesem Problem geht es darum, dass ein Museumsdirektor sicherstellen möchte, dass jeder Punkt seines Museums überwacht wird. Dafür werden Museumswächterinnen an festen Stellen im Museum platziert, dürfen sich aber drehen. Nun lautet die Frage, wie viele Wächterinnen benötigt werden, um das Museum zu überwachen.
Museum Ritter
Zuerst betrachten wir das Museum Ritter, welches zum gleichnamigen Schokoladenhersteller gehört. Natürlich ist der Grundriss in unserer idealisierten Mathewelt perfekt quadratisch. Der Museumsdirektor möchte nun Museumswächterinnen einstellen und fragt sich, wie viele Leute er anstellen muss, wenn eine Wächterin sich zwar nicht frei im Raum bewegen, aber sich um ihre Achse drehen darf. Die Antwort auf die Frage ist trivial, es reicht, eine Wächterin irgendwo im Raum zu positionieren, wie relativ direkt aus der Definition der Konvexität folgt. Wie sieht es aber aus, wenn das Museum einen etwas komplizierteren Grundriss besitzt?
Satz
Nun betrachten wir ein Museum mit einem beliebigen Grundriss, welcher allerdings komplexer ist als der Grundriss des Museum Ritter. Einzige Voraussetzung ist, dass sich alle Wände durch eine Gerade beschreiben lassen. Nun möchte unser Museumsdirektor wieder Wächterinnen einstellen und fragt sich, wie viele er braucht, damit diese das komplette Museum im Blick haben. Auch hier gilt wieder, dass sich die Wächterinnen nicht hin und her bewegen, sondern auf ihren Plätzen bleiben und sich nur um ihre Achse drehen können. Dann benötigt man folgende Anzahl an Wächterinnen:
Für jedes Museum mit [math]n[/math] Wänden reichen [math]\lfloor \frac{n}{3} \rfloor[/math] Wächterinnen aus.
Dabei bedeuten die sogenannten Gaußklammern [math]\lfloor\, \rfloor[/math], dass der Nachkommateil des Qoutienten [math] \frac{n}{3}[/math], abgeschnitten, dieser also auf die nächstkleinere ganze Zahl abgerundet wird.
Beweis nach Steve Fisk
Um diesen Satz zu beweisen, müssen wir zuerst das Museum mathematisch beschreiben können. Dazu führen wir einige Definitionen ein:
Definition: Polygon
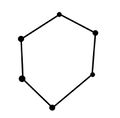
Ein Polygon ist ein Tupel [math]P= \left(P_1,P_2,\dots,P_n \right)[/math], von n verschiedenen Punkten [math]P_i\ (\text{mit}\ 1\leq i\leq n,\ n\in\mathbb{N})[/math]. Dabei heißen die [math]n[/math] Punkte Eckpunkte des Polygons (man spricht auch von einem [math]n[/math]-Eck) und die Strecken [math]\overline{P_iP_{i+1}}[/math] für [math] (1\leq i\leq n-1)[/math] und [math]\overline{P_1P_n}[/math] zwischen den Eckpunkten werden als Kanten oder Seiten bezeichnet.
Die Verbindungsstrecken zweier Punkte die keinen Kanten sind werden als Diagonalen bezeichnet.
In unserem Fall betrachten wir nur planare Polygone, das heißt n-Ecke, welche in der Ebene liegen. Zusätzlich kann es sein, dass sich die Kanten nicht nur in den Eckpunkten schneiden, in diesem Fall spricht man von einem überschlagenen Polygon.
Definition: Triangulierung
Als Triangulation eines Polygons bezeichnen wir hier einen planaren Graph, welcher entsteht, wenn man die Innenfläche des Polygons durch Diagonalen, welche sich nicht schneiden, mit Dreiecken ausfüllt.
Für konvexe Polygone ist klar, dass eine Triangulation immer möglich ist
Satz: Für alle planaren Polygone P existiert eine Triangulation
Beweis: Wir zeigen nun per vollständiger Induktion die Aussage für allgemeine planare Polygone. Sei n die Zahl der Ecken.
IA: für [math]n=3[/math] ist [math]P[/math] ein Dreieck also schon trianguliert.
IV: Der Satz gilt für alle Polygone mit weniger als [math]n[/math] Ecken
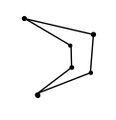
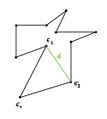
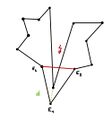
IS: [math](n-1)\rightarrow n[/math] Wir suchen eine Diagonale, die P in zwei Polygone [math]P_1[/math] und [math]P_2[/math] teilt. Dazu nehmen wir eine Ecke [math]E_1[/math] mit Innenwinkel kleiner als 180° (existiert immer) und verbinden die beiden zu [math]E_1[/math] benachbarten Ecken [math]E_2[/math] und [math]E_3[/math]. Nun sind 2 Fälle möglich:
Fall 1: [math]\overline{E_2E_3}[/math] ist vollständig in P enthalten. Dann ist mit dieser Diagonal das Polygon in zwei Polygone zerteilt mit jeweils weniger als n Ecken. Nach IV sind diese dann natürlich triangulierbar. Damit folgt die Behauptung auch für das gesamte Polygon.
Fall 2: [math]\overline{E_2E_3}[/math] ist nicht vollständig in P enthalten. Dann liegt also mindestens eine Ecke des Polygons innerhalb des Dreiecks [math]E_1E_2E_3[/math] und kann durch eine Diagonale mit [math]E_1[/math] verbunden werden. Somit lässt sich das Polygon in 2 Polygone mit je weniger als n Ecken teilen, womit nach IV ebenfalls die Behauptung erfüllt ist.
Bemerkung: Im 3-dimensionalen ist eine Triangulation durch Tetraeder im Allgemeinen nicht möglich (vgl. Schönhardt-Polyeder).
Definition: Färbung
Sei E die Menge der Ecken eines Polygons und F die abzählbare Menge der Farben (oder Eigenschaften). Eine Färbung [math]f[/math] ordnet jeder Ecke eine Farbe zu, es handelt sich also um eine Abbildung [math]f: E\rightarrow F[/math]
Wir nennen eine Färbung eine 3-Färbung, falls:
(i) [math]\# F=3[/math]
(ii) je 2 benachbarte Ecken stets verschiedene Farben haben
Satz: Jede Triangulation eines Polygons P ist 3-färbbar
Beweis: Wir zeigen die Aussage per vollständige Induktion.
IA: Für [math]n=3[/math] ist P ein Dreieck und somit die Aussage trivialerweise erfüllt.
IV: Gelte der Satz für Polygone mit weniger als n Ecken
IS: [math]n-1 \rightarrow n[/math] Wir betrachten eine beliebige Triangulierung von [math]P[/math] und wählen zwei beliebige Ecken [math]E_1[/math] und [math]E_2[/math], welche durch eine Diagonale [math]\overline{E_1E_2}[/math] verbunden sind. Da diese das Polygon in zwei Polygone mit weniger als [math]n[/math] Ecken teilt, lässt sich die Induktionsvoraussetzung anwenden, womit die Aussage auch für das zusammengesetze Polygon gilt (seien hierfür o. B. d. A. in beiden Polygonen die Farben von [math]E_1[/math] und [math]E_2[/math] gleich gewählt).
Finaler Beweis des Museumswächterproblems nach Fisk:
Für ein Museum mit [math]n=3[/math] Ecken ist die Anzahl der Wächterinnen klar. Für ein Museum mit [math]n\gt 3[/math] Ecken beschreiben wir den Grundriss als Polygon, wobei die Anzahl der Ecken derjenigen der Wände entspricht. Wir nutzen nun, dass jedes Polygon triangulierbar und jede Triangulation 3-färbbar ist, wir wählen hierfür o.B.d.A die Farben rot, blau und orange. Mindestens eine dieser Farben muss damit maximal [math]\lfloor \frac{n}{3} \rfloor[/math]-mal vertreten sein, wenn [math]n[/math] die Gesamtzahl der Ecken bezeichnet. In unserer Triangulierung besitzt jedes einzelne Dreieck nach Konstruktion eine rote, eine blaue und eine gelbe Ecke. Besetzt man also alle Ecken einer Farbe mit einer Museumswächterin, so lässt sich jedes Dreieck (Dreiecke sind konvex) und damit das gesamte Museum einsehen. Somit reichen in jedem Museum [math]\lfloor \frac{n}{3} \rfloor[/math] Wächterinnen aus, um das gesamte Museum zu überblicken.
Beispielrechnung am Guggenheim-Museum Bilbao
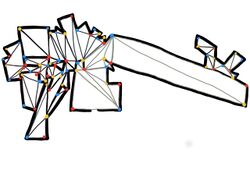
Da er das Museum Ritter so gut mit Wächterinnen ausgestattet hat, wurde der Direktor befördert und arbeitet nun im renommierten Guggenheim-Museum in Bilbao. Auch hier soll er wieder Wärterinnen anstellen und zwar wieder zu den gleichen Bedingungen wie zuvor. Sie werden also wieder in Ecken positioniert, in denen sie sich drehen, aber nicht ihren Posten verlassen dürfen. Dazu wird, wie in der Nebenstehenden Graphik gezeigt, der Grundriss des Museums trianguliert. Anschließend werden die Ecken wieder gefärbt und gezählt. Dabei ergibt sich eine Anzahl von 27 roten Ecken, 27 orange Ecken und 28 blauen Ecken, also bräuchte man 27 Wächterinnen. Um zu überprüfen, ob sich der Direktor nicht verzählt hat, wendet er noch den Satz des Museumswächterinnenproblems an. Dazu zählt er alle Wände und kommt auf eine Anzahl von insgesamt 85. Nun strengt er seine grauen Zellen an und errechnet damit, dass er höchstens [math] \lfloor \frac{82}{3} \rfloor =27 [/math] Wächterinnen braucht. Dies stimmt mit seinen Erwartungen überein und er ist sehr glücklich.
Guggenheim-Museum in Bilbao[1]
Triangulierung des Grundrisses des Mueseums
Trivia
Nach ungenauen Berechnungen des Museumsdirektors wird er aus dem Guggenheim-Museum in Bilbao entlassen. So kehrt er ins Museum Ritter zurück. Voller Schreck entdeckt er, dass sich das Museum ja komplett verändert hat. Anstatt eines einfachen Quadrates ist er nun Leiter des realen Museum Ritter, welches im Inneren Wände hat. Zum Glück hat der Direktor in Bilbao genügend Erfahrung im Triangulieren gesammelt, weswegen es nun ein Leichtes für ihn ist, auch das Museum Ritter, mit dem neuen Grundriss, ideal mit Wächterinnen zu besetzen.
Das reale Museum Ritter[2]
Triangulierung des realen Museum Ritter
Ausblick
Nach den langen Reisen unseres lieben Museumdirektors vom Museum Ritter in das Guggenheim-Museum in Bilbao und wieder zurück zum Museum Ritter, überlegt sich der Museumdirektor, was es denn noch für spannende Museen und Aufgaben für Wächterinnen gäben könnte.
So denkt er sich, wieviele Wächterinnen es in einem Museum, welches ein orthogonales Polyeder ist, bräuchte. [math]\lfloor\frac{n}{4}\rfloor[/math] schießt ihm sofort in den Kopf.
Auch hat der Direktor die Überlegung, dass die Wächterinnen die Wände entlang gehen und von jedem Punkt an der Wand in den Raum hineinschauen können. Wieviele Wächterinnen bräuchten er dann?
Und was passiert in Museen, die dreidimensional sind? Wieviele Wächterinnen braucht der Direktor in einem Museum mit Gängen, die quer durch den Raum gehen?
Aber nach all seinen Expeditionen ist er zu müde um auch das noch zu beweisen.
Quellen
- Das BUCH der Beweise. Springer, Berlin 2018 (5. Auflage: ISBN 978-3-662-57766-0).
- https://imsc.uni-graz.at/baur/lehre/WS2013-Seminar/S9.pdf, Stand 25.03.2021
- http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.67.8231&rep=rep1&type=pdf, Stand 25.03.2021
- Grundriss des Museums frei nach https://de.wikiarquitectura.com/geb%C3%A4ude/guggenheim-bilbao/, Stand 25.03.2021
Autoren
Julie Drhova, Joris Hoffmann, Hjalmar Brunßen, Lasse Bassermann