PageRank-Algorithmus: Unterschied zwischen den Versionen
Ru251 (Diskussion | Beiträge) K (→Beispiel) |
Ru251 (Diskussion | Beiträge) K (→Autoren) |
||
| (21 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 2: | Zeile 2: | ||
== Hyperlink-Übergangsmatrix == | == Hyperlink-Übergangsmatrix == | ||
| − | Die Grundlage für unsere Überlegungen bildet eine quadratische Matrix, mit einer Spalte für jede | + | Die Grundlage für unsere Überlegungen bildet eine quadratische Matrix, mit einer Spalte für jede Website im Internet. Wir betrachten nun für jede Website die Links auf dieser, wobei doppelte nur einfach gezählt werden. Dass eine solche Verbindung zwischen zwei Websites besteht, soll jetzt, wie bei einer [https://de.wikipedia.org/wiki/Adjazenzmatrix#:~:text=%2DMatrix%20ergibt.,Kante%20existiert%2C%20siehe%20Abbildung%20rechts. Adjazenzmatrix] in das entsprechende Feld unserer Hyperlink-Matrix eingetragen werden. Anders als bei der Adjazenzmatrix, in der jeder Eintrag gleich eins ist, wenn der entsprechende Knoten von dem Anfangsknoten erreicht werden kann, führen wir hier eine Abwandlung durch: bei der Hyperlink-Matrix werden die Einträge so angepasst, dass die Summe der Spalten stets eins ergibt. Da es für die Berechnung der Ranks später einfacher ist, stellen wir die Hyperlink-Matrix so auf, dass die Website von welcher wir ausgehen durch die jeweilige Spalte repräsentiert wird und die Zielseiten sich in den Zeilen wiederfinden (transponiert im Vergleich zu der [https://de.wikipedia.org/wiki/Adjazenzmatrix#:~:text=%2DMatrix%20ergibt.,Kante%20existiert%2C%20siehe%20Abbildung%20rechts. Adjazenzmatrix]). |
Sei nun <math>H</math> unsere Hyperlinkmatrix, <math>n_j</math> die Anzahl der Links, die von der <math>j</math>-ten Website auf andere Websites verweisen. | Sei nun <math>H</math> unsere Hyperlinkmatrix, <math>n_j</math> die Anzahl der Links, die von der <math>j</math>-ten Website auf andere Websites verweisen. | ||
| Zeile 8: | Zeile 8: | ||
<math>h_{ij}=\begin{cases} | <math>h_{ij}=\begin{cases} | ||
| − | \frac{1}{ | + | \frac{1}{n_{j}}, \quad \text{falls unsere } j\text{-te Seite einen Link auf die } i\text{-te Seite besitzt}\\ |
| − | 0 \quad \text{ sonst} | + | 0, \quad \text{ sonst} |
\end{cases} | \end{cases} | ||
</math> | </math> | ||
Das heißt, die Summe jeder einzelnen Spalte ergibt immer eins und auf der Diagonalen von <math>H</math> stehen nur Nullen, da eine Website sich nicht selbst verlinkt. | Das heißt, die Summe jeder einzelnen Spalte ergibt immer eins und auf der Diagonalen von <math>H</math> stehen nur Nullen, da eine Website sich nicht selbst verlinkt. | ||
| + | |||
| + | In Realität ist diese Matrix natürlich riesig, da es für jeden Suchbegriff sehr viele Websites gibt, die diesen beinhalten. Zur Veranschaulichung werden wir uns im Folgenden allerdings mit einem sehr stark vereinfachten Internet mit nur wenigen Websites befassen. | ||
===Beispiel=== | ===Beispiel=== | ||
| − | Betrachten wir nun folgendes | + | Betrachten wir nun folgendes Internet (die Pfeile stellen die Links dar) und stellen die entsprechende Matrix auf: <gallery widths="300" heights="200"> |
Datei:Internet 2 (1).jpg | Datei:Internet 2 (1).jpg | ||
</gallery> | </gallery> | ||
| − | Betrachten wir nun die erste Spalte unserer Matrix, also die Website <math>A</math> und zu welchen Seiten sie einen Link besitzt. Es gibt einen Pfeil nach <math>B</math> und einen nach <math>D</math>. Insgesamt gehen also zwei Links von <math>A</math> weg, das heißt <math>n = 2</math>. Die erste Spalte sieht deswegen wie folgt aus: | + | Betrachten wir nun die erste Spalte unserer Matrix, also die Website <math>A</math> und zu welchen Seiten sie einen Link besitzt. Es gibt einen Pfeil nach <math>B</math> und einen nach <math>D</math>. Insgesamt gehen also zwei Links von <math>A</math> weg, das heißt <math>n = 2</math>. Da auf der Website <math>A</math> zwei andere Websites verlinkt sind, sind die Einträge jeweils <math>\frac{1}{2}</math>. Die erste Spalte sieht deswegen wie folgt aus: |
<math>\begin{pmatrix} | <math>\begin{pmatrix} | ||
| Zeile 29: | Zeile 31: | ||
\end{pmatrix}</math> | \end{pmatrix}</math> | ||
| − | + | Auf Website <math>C</math> sind hingegen drei weitere Websites verlinkt sind, nämlich <math>A</math>, <math>B</math> und <math>E</math>. Das heißt, hier sind die Einträge jeweils <math>\frac{1}{3}</math>. Die dritte Spalte sieht also wie folgt aus: | |
<math>\begin{pmatrix} | <math>\begin{pmatrix} | ||
| Zeile 50: | Zeile 52: | ||
== Prinzip des PageRank-Algorithmus == | == Prinzip des PageRank-Algorithmus == | ||
| − | Eine Website ist umso wichtiger, um so mehr Links von wichtigen Websites auf sie verweisen. Dies soll jetzt in ''einer'' Zahl ausgedrückt werden. Sei also <math> | + | Eine Website ist umso wichtiger, um so mehr Links von wichtigen Websites auf sie verweisen. Dies soll jetzt in ''einer'' Zahl ausgedrückt werden. Sei also <math>A</math> eine Website mit PageRank <math>R(A)</math>, für eine beliebige Seite <math>X</math> sei <math>n_X</math> die Anzahl der (verschiedenen) Links, die auf <math>X</math> vorkommen. Sei zudem <math>B_A</math> die Menge der Websites, die einen Link zu <math>A</math> besitzen. Dann lässt sich der Grundgedanke von PageRank durch die folgende rekursive Formel ausdrücken: |
| − | <math>R( | + | <math>R(A) = \sum_{X \in B_A} \frac{R(X)}{n_X} </math>. |
| − | + | In Worten formuliert: Der Rank einer Seite <math>A</math> ergibt sich als eine Art gewichteter Durchschnitte der Ranks der Seiten <math>X \in B_A</math>, wobei durch <math>n_X</math> geteilt wird, denn würde man einfach die Summe der Ranks der Seiten in <math>B_a</math> betrachten, so würden Seiten mit sehr vielen Links unter Umständen viel stärker ins Gewicht fallen als etwa Seiten mit nur einem Link darauf. | |
| − | + | Bei dieser rekursiven Definition muss man zur Berechnung eines PageRanks die PageRanks anderer Websites kennen. Es bleibt also nichts, als alle diese Gleichungen simultan zu lösen (LGS!). Wir versuchen also diese Gleichungen in LA-Sprache zu übersetzen, wobei wir von der Matrix aus dem vorigen Abschnitt Gebrauch machen. | |
| − | Sei <math>w</math> der Spaltenvektor mit den PageRank-Werten der einzelnen Seiten (<math>i</math>-te Komponente zu <math>i</math>-ter Website). | + | Sei <math>w</math> der Spaltenvektor mit den PageRank-Werten der einzelnen Seiten (<math>i</math>-te Komponente zu <math>i</math>-ter Website). Man kann sich anhand der Definition der Matrixmultiplikation leicht überlegen, dass das obige LGS äquivalent ist zu <math>Hw = w</math>. |
| − | Wir erkennen eine bekannte Form: es handelt sich hier um ein Eigenvektorproblem. Zunächst müssen wir zwei Dinge abhaken. Erstens müssen wir klären, dass es überhaupt eine nicht-triviale Lösung <math>w</math> gibt, zweitens muss man sich fragen, wieso diese, mit der Zusatzbedingung, dass die Summe der Einträge in <math>w</math> gleich 1 ist, eindeutig ist. | + | Wir erkennen eine bekannte Form: es handelt sich hier um ein Eigenvektorproblem. Zunächst müssen wir zwei Dinge abhaken. Erstens müssen wir klären, dass es überhaupt eine nicht-triviale Lösung <math>w</math> gibt, zweitens muss man sich fragen, wieso diese, mit der Zusatzbedingung, dass die Summe der Einträge in <math>w</math> gleich 1 ist, eindeutig ist. Die Klärung dieser beiden Fragen würde hier zu weit gehen, doch im Abschnitt zu den Markow-Ketten wird eine Interpretation und damit eine Erklärung zumindest angedeutet. |
Im nächsten Abschnitt wollen wir diese Lösung iterativ berechnen. | Im nächsten Abschnitt wollen wir diese Lösung iterativ berechnen. | ||
| Zeile 67: | Zeile 69: | ||
Dazu nutzen wir ein Ergebnis aus der LA (Potenzmethode): | Dazu nutzen wir ein Ergebnis aus der LA (Potenzmethode): | ||
| − | ''Betrachtet man eine diagonalisierbare Matrix A, so gibt es eine Basis aus den Eigenvektoren zu den entsprechenden Eigenwerten. Betrachte nun die Eigenwerte und sortiere sie nach der Größe des Betrags, sodass gilt <math> |λ_{1}|>|λ_{2}|\geq ... \geq |λ_{n}| </math>.Nun wählen wir einen Startvektor und erhalten eine Folge <math> (v^{(i)}) </math>, die durch sukzessives Anwenden von A definiert ist. Es gilt: <math> v^ {(i+1)} = Av^ {(i)} </math>. Diese Folge konvergiert bei geeigneter Wahl von dem Startvektor gegen einen Eigenvektor v der Matrix A zum Eigenwert <math> λ_{1} </math>. Falls also k groß genug ist, gilt: <math>Av^{(k)} \approx λ_{1}v^{(k)} </math>. | + | {| class="wikitable left mw-collapsible mw-collapsed font-size: 100%;" |
| − | + | | style="text-align:left; font-size: 100%;" | '''Die Potenzmethode''' | |
| − | In der Anwendung wählen wir einfach einen Startvektor, etwa einen Einheitsvektor und multiplizieren iterativ <math>H</math> von links. Wir erhalten (unter geeigneten Startbedingungen) Konvergenz gegen einen Eigenvektor zum Eigenwert 1, denn es gibt hier keine größeren Eigenwerte als 1. Dieser stellt dann eine Lösung des LGS dar und enthält damit die gesuchten Page-Ranks. | + | |- |
| + | | Betrachtet man eine diagonalisierbare Matrix A, so gibt es eine Basis aus den Eigenvektoren zu den entsprechenden Eigenwerten. Betrachte nun die Eigenwerte und sortiere sie nach der Größe des Betrags, sodass gilt <math> |λ_{1}|>|λ_{2}|\geq ... \geq |λ_{n}| </math>. Nun wählen wir einen Startvektor und erhalten eine Folge <math> (v^{(i)}) </math>, die durch sukzessives Anwenden von A definiert ist. Es gilt: <math> v^ {(i+1)} = Av^ {(i)} </math>. Diese Folge konvergiert bei geeigneter Wahl von dem Startvektor gegen einen Eigenvektor v der Matrix A zum Eigenwert <math> λ_{1} </math>. Falls also k groß genug ist, gilt: <math>Av^{(k)} \approx λ_{1}v^{(k)} </math>. | ||
| + | |} | ||
| + | |||
| + | In der Anwendung wählen wir einfach einen Startvektor, etwa einen Einheitsvektor und multiplizieren iterativ <math>H</math> von links daran. Wir erhalten (unter geeigneten Startbedingungen) Konvergenz gegen einen Eigenvektor zum Eigenwert 1, denn es gibt hier keine größeren Eigenwerte als 1. Dieser stellt dann eine Lösung des LGS dar und enthält damit die gesuchten Page-Ranks. | ||
===Beispiel=== | ===Beispiel=== | ||
| Zeile 114: | Zeile 120: | ||
\end{pmatrix}</math> | \end{pmatrix}</math> | ||
| − | Dies ist der Eigenvektor zum Eigenwert 1 unserer Matrix <math>H</math>. Eine andere Möglichkeit zur Berechnung dieses Vektors ist, zunächst die Matrix ausreichend oft zu potenzieren und anschließend den Vektor <math>v</math> von rechts zu multiplizieren. Das funktioniert, da gilt <math> | + | Dies ist der Eigenvektor zum Eigenwert 1 unserer Matrix <math>H</math>. Eine andere Möglichkeit zur Berechnung dieses Vektors ist, zunächst die Matrix ausreichend oft zu potenzieren und anschließend den Vektor <math>v</math> von rechts zu multiplizieren. Das funktioniert, da gilt <math>(H^i)v=H(\cdots (H(Hv))\cdots)</math>. |
==Markow-Ketten== | ==Markow-Ketten== | ||
| − | Jetzt wollen wir eine schöne und intuitive Sichtweise dafür geben, was hier passiert. Das ist die Theorie der Markow-Ketten (hier sehr seicht abgehandelt!). Dabei geht es um eine Menge von Zuständen mit Übergangswahrscheinlichkeiten zwischen diesen. Hier stellt unsere Menge der | + | Jetzt wollen wir eine schöne und intuitive Sichtweise dafür geben, was hier passiert. Das ist die Theorie der Markow-Ketten (hier sehr seicht abgehandelt!). Dabei geht es um eine Menge von Zuständen mit Übergangswahrscheinlichkeiten zwischen diesen. Hier stellt unsere Menge der Websites die Zustandsmenge dar und die Matrix <math>H</math> die Übergangsmatrix. Die Interpretation ist die, dass ein zufälliger Surfer von einer beliebigen Website einen der Links zufällig anklickt und dann auf einer der anderen Websites landet. Das erklärt auch wieso sich die Spalten von <math>H</math> zu 1 ergänzen sollten. Multipliziert man z. B. die Übergangsmatrix an den ersten Einheitsvektor, so erhält man die Wahrscheinlichkeiten, wo der zufällige Surfer sich nach einem Schritt befindet, wenn er auf der ersten Website gestartet ist. |
| − | Potenziert man diese Übergangsmatrix, etwa <math>H^k</math>, so erhält man in den Zellen die Übergangswahrscheinlichkeiten von einem Zustand (Spalte) zu einem anderen (Zeile) in genau <math>k</math> Übergangsschritten. Das kann man sich leicht anhand der Matrixmultiplikation überlegen. Der Gedanke liegt nahe, dass diese Matrixpotenzen konvergieren, denn irgendwann spielen die Einzelübergänge keine große Rolle mehr; man erhält | + | Potenziert man diese Übergangsmatrix, etwa <math>H^k</math>, so erhält man in den Zellen die Übergangswahrscheinlichkeiten von einem Zustand (Spalte) zu einem anderen (Zeile) in genau <math>k</math> Übergangsschritten. Das kann man sich leicht anhand der Matrixmultiplikation überlegen. Der Gedanke liegt nahe, dass diese Matrixpotenzen konvergieren, denn irgendwann spielen die Einzelübergänge keine große Rolle mehr; man erhält eine Matrix mit lauter gleichen Spalten (das kann man mit [https://matrixcalc.org/de/ Matrixcalc] sehr gut ausprobieren!). Das liegt daran, dass die Multiplikation mit jedem stochastischen Vektor (das ist ein Spaltenvektor mit nicht negativen Einträgen, die sich zu 1 ergänzen), wie etwa einem der Einheitsvektoren das gleiche ergibt: der Start spielt keine Rolle mehr, man erhält im Grenzwert eine Aufenthaltswahrscheinlichkeit für jeden der Zustände. Man spricht von der eindeutigen ''stationären Verteilung'' der Markow-Kette. Diese ist genau der PageRank! Sie ist also ein Maß dafür, wie viel Zeit der zufällige Surfer im stochastischen Sinn auf den einzelnen Websites verbringt und gibt somit Aufschluss über die wichtigsten Seiten. |
Die oben beschriebene Konvergenz findet allerdings nur unter gewissen Voraussetzungen statt. Um diese soll es jetzt kurz gehen: | Die oben beschriebene Konvergenz findet allerdings nur unter gewissen Voraussetzungen statt. Um diese soll es jetzt kurz gehen: | ||
| Zeile 152: | Zeile 158: | ||
</gallery> | </gallery> | ||
| − | Hier liegen | + | Hier liegen zwei Websites vor, die jeweils nur die andere verlinken. So kommt es dazu, dass wir langfristig immer zwischen den beiden hin- und herspringen und die Bedingung somit verletzt ist. |
==Verbesserungen - Der Dämpfungsfaktor== | ==Verbesserungen - Der Dämpfungsfaktor== | ||
| Zeile 203: | Zeile 209: | ||
Wir sehen, dass die Summe aller Einträge in einer Spalte immer noch eins ergibt. Allerdings hat die Matrix <math>H'</math> keine einzige 0 mehr als Eintrag, insbesondere auch nicht auf der Diagonalen (Websites verweisen jetzt auch auf sich selbst). Das heißt, dass es möglich ist, von jeder Website auf jede andere zu kommen. Es gibt also keine Sackgassen mehr, es können sich keine Gruppen bilden und erreicht man eine Website in <math>k</math> Schritten, so erreicht man sie sicherlich auch in <math>k' (k'>k)</math> Schritten. Genau das, was wir mit dem Dämpfungsfaktor erreichen wollten! | Wir sehen, dass die Summe aller Einträge in einer Spalte immer noch eins ergibt. Allerdings hat die Matrix <math>H'</math> keine einzige 0 mehr als Eintrag, insbesondere auch nicht auf der Diagonalen (Websites verweisen jetzt auch auf sich selbst). Das heißt, dass es möglich ist, von jeder Website auf jede andere zu kommen. Es gibt also keine Sackgassen mehr, es können sich keine Gruppen bilden und erreicht man eine Website in <math>k</math> Schritten, so erreicht man sie sicherlich auch in <math>k' (k'>k)</math> Schritten. Genau das, was wir mit dem Dämpfungsfaktor erreichen wollten! | ||
| − | Der Dämpfungsfaktor schafft also erst Platz, indem wir die Matrix mit <math>d</math> multiplizieren, sodass wir dann überall noch <math>\frac{1-d}{N}</math> addieren können, ohne die Summe 1 (also 100%) zu überschreiten. Somit werden jegliche Verletzungen der drei Voraussetzungen aufgefangen, ohne, dass das eigentliche Ergebnis verfälscht wird. | + | Der Dämpfungsfaktor schafft also erst Platz, indem wir die Matrix mit <math>d</math> multiplizieren, sodass wir dann überall noch <math>\frac{1-d}{N}</math> addieren können, ohne die Summe 1 (also 100%) zu überschreiten. Somit werden jegliche Verletzungen der drei Voraussetzungen aufgefangen, ohne, dass das eigentliche Ergebnis zu sehr verfälscht wird. |
==Quellen und weiterführende Links== | ==Quellen und weiterführende Links== | ||
| Zeile 210: | Zeile 216: | ||
* https://de.wikipedia.org/wiki/Google-Matrix | * https://de.wikipedia.org/wiki/Google-Matrix | ||
* Arens, T. (et al.): Mathematik, Springer 2008 | * Arens, T. (et al.): Mathematik, Springer 2008 | ||
| + | |||
| + | ==Autoren== | ||
| + | Mathis, Julia | ||
Aktuelle Version vom 13. April 2021, 08:36 Uhr
Es gibt mehrere Milliarden Websites im Internet und doch erscheint, wenn wir bei Google beispielsweise nach "Fun Facts Heidelberg" suchen, die Vorlesungsseite in verschiedenen Browsern unter den ersten zehn. Das liegt daran, dass der Suchbegriff auf einigen der Seiten keine so große Rolle spielt. Man wird feststellen, dass die ersten Ergebnisse die relevantesten sind. Aber wie schafft es die Suchmaschine die Seiten so zu sortieren? Dort kommt der PageRank-Algorithmus ins Spiel, welcher die Seiten über die Anzahl an Links mit Hilfe von linearer Algebra nach ihrer Wichtigkeit sortiert.
Hyperlink-Übergangsmatrix
Die Grundlage für unsere Überlegungen bildet eine quadratische Matrix, mit einer Spalte für jede Website im Internet. Wir betrachten nun für jede Website die Links auf dieser, wobei doppelte nur einfach gezählt werden. Dass eine solche Verbindung zwischen zwei Websites besteht, soll jetzt, wie bei einer Adjazenzmatrix in das entsprechende Feld unserer Hyperlink-Matrix eingetragen werden. Anders als bei der Adjazenzmatrix, in der jeder Eintrag gleich eins ist, wenn der entsprechende Knoten von dem Anfangsknoten erreicht werden kann, führen wir hier eine Abwandlung durch: bei der Hyperlink-Matrix werden die Einträge so angepasst, dass die Summe der Spalten stets eins ergibt. Da es für die Berechnung der Ranks später einfacher ist, stellen wir die Hyperlink-Matrix so auf, dass die Website von welcher wir ausgehen durch die jeweilige Spalte repräsentiert wird und die Zielseiten sich in den Zeilen wiederfinden (transponiert im Vergleich zu der Adjazenzmatrix).
Sei nun [math]H[/math] unsere Hyperlinkmatrix, [math]n_j[/math] die Anzahl der Links, die von der [math]j[/math]-ten Website auf andere Websites verweisen. Der Eintrag an der Stelle [math]h_{ij}[/math] ist dann also wie folgt:
[math]h_{ij}=\begin{cases} \frac{1}{n_{j}}, \quad \text{falls unsere } j\text{-te Seite einen Link auf die } i\text{-te Seite besitzt}\\ 0, \quad \text{ sonst} \end{cases} [/math]
Das heißt, die Summe jeder einzelnen Spalte ergibt immer eins und auf der Diagonalen von [math]H[/math] stehen nur Nullen, da eine Website sich nicht selbst verlinkt.
In Realität ist diese Matrix natürlich riesig, da es für jeden Suchbegriff sehr viele Websites gibt, die diesen beinhalten. Zur Veranschaulichung werden wir uns im Folgenden allerdings mit einem sehr stark vereinfachten Internet mit nur wenigen Websites befassen.
Beispiel
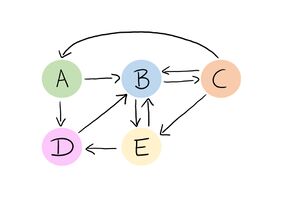
Betrachten wir nun folgendes Internet (die Pfeile stellen die Links dar) und stellen die entsprechende Matrix auf:
Betrachten wir nun die erste Spalte unserer Matrix, also die Website [math]A[/math] und zu welchen Seiten sie einen Link besitzt. Es gibt einen Pfeil nach [math]B[/math] und einen nach [math]D[/math]. Insgesamt gehen also zwei Links von [math]A[/math] weg, das heißt [math]n = 2[/math]. Da auf der Website [math]A[/math] zwei andere Websites verlinkt sind, sind die Einträge jeweils [math]\frac{1}{2}[/math]. Die erste Spalte sieht deswegen wie folgt aus:
[math]\begin{pmatrix} 0\\ \frac{1}{2}\\ 0\\ \frac{1}{2}\\ 0 \end{pmatrix}[/math]
Auf Website [math]C[/math] sind hingegen drei weitere Websites verlinkt sind, nämlich [math]A[/math], [math]B[/math] und [math]E[/math]. Das heißt, hier sind die Einträge jeweils [math]\frac{1}{3}[/math]. Die dritte Spalte sieht also wie folgt aus:
[math]\begin{pmatrix} \frac{1}{3}\\ \frac{1}{3}\\ 0\\ 0\\ \frac{1}{3} \end{pmatrix}[/math]
Die anderen Spalten folgen analog und wir gelangen zu folgender Hyperlink-Matrix:
[math]H=\begin{pmatrix} 0 & 0 & \frac{1}{3} & 0 & 0\\ \frac{1}{2} & 0 & \frac{1}{3} & 1 & \frac{1}{2}\\ 0 & \frac{1}{2} & 0 & 0 & 0\\ \frac{1}{2} & 0 & 0 & 0 & \frac{1}{2}\\ 0 & \frac{1}{2} & \frac{1}{3} & 0 & 0 \end{pmatrix}[/math]
Prinzip des PageRank-Algorithmus
Eine Website ist umso wichtiger, um so mehr Links von wichtigen Websites auf sie verweisen. Dies soll jetzt in einer Zahl ausgedrückt werden. Sei also [math]A[/math] eine Website mit PageRank [math]R(A)[/math], für eine beliebige Seite [math]X[/math] sei [math]n_X[/math] die Anzahl der (verschiedenen) Links, die auf [math]X[/math] vorkommen. Sei zudem [math]B_A[/math] die Menge der Websites, die einen Link zu [math]A[/math] besitzen. Dann lässt sich der Grundgedanke von PageRank durch die folgende rekursive Formel ausdrücken:
[math]R(A) = \sum_{X \in B_A} \frac{R(X)}{n_X} [/math].
In Worten formuliert: Der Rank einer Seite [math]A[/math] ergibt sich als eine Art gewichteter Durchschnitte der Ranks der Seiten [math]X \in B_A[/math], wobei durch [math]n_X[/math] geteilt wird, denn würde man einfach die Summe der Ranks der Seiten in [math]B_a[/math] betrachten, so würden Seiten mit sehr vielen Links unter Umständen viel stärker ins Gewicht fallen als etwa Seiten mit nur einem Link darauf. Bei dieser rekursiven Definition muss man zur Berechnung eines PageRanks die PageRanks anderer Websites kennen. Es bleibt also nichts, als alle diese Gleichungen simultan zu lösen (LGS!). Wir versuchen also diese Gleichungen in LA-Sprache zu übersetzen, wobei wir von der Matrix aus dem vorigen Abschnitt Gebrauch machen.
Sei [math]w[/math] der Spaltenvektor mit den PageRank-Werten der einzelnen Seiten ([math]i[/math]-te Komponente zu [math]i[/math]-ter Website). Man kann sich anhand der Definition der Matrixmultiplikation leicht überlegen, dass das obige LGS äquivalent ist zu [math]Hw = w[/math].
Wir erkennen eine bekannte Form: es handelt sich hier um ein Eigenvektorproblem. Zunächst müssen wir zwei Dinge abhaken. Erstens müssen wir klären, dass es überhaupt eine nicht-triviale Lösung [math]w[/math] gibt, zweitens muss man sich fragen, wieso diese, mit der Zusatzbedingung, dass die Summe der Einträge in [math]w[/math] gleich 1 ist, eindeutig ist. Die Klärung dieser beiden Fragen würde hier zu weit gehen, doch im Abschnitt zu den Markow-Ketten wird eine Interpretation und damit eine Erklärung zumindest angedeutet.
Im nächsten Abschnitt wollen wir diese Lösung iterativ berechnen.
Iterative Berechnung der Lösung
Dazu nutzen wir ein Ergebnis aus der LA (Potenzmethode):
| Die Potenzmethode |
| Betrachtet man eine diagonalisierbare Matrix A, so gibt es eine Basis aus den Eigenvektoren zu den entsprechenden Eigenwerten. Betrachte nun die Eigenwerte und sortiere sie nach der Größe des Betrags, sodass gilt [math] |λ_{1}|\gt |λ_{2}|\geq ... \geq |λ_{n}| [/math]. Nun wählen wir einen Startvektor und erhalten eine Folge [math] (v^{(i)}) [/math], die durch sukzessives Anwenden von A definiert ist. Es gilt: [math] v^ {(i+1)} = Av^ {(i)} [/math]. Diese Folge konvergiert bei geeigneter Wahl von dem Startvektor gegen einen Eigenvektor v der Matrix A zum Eigenwert [math] λ_{1} [/math]. Falls also k groß genug ist, gilt: [math]Av^{(k)} \approx λ_{1}v^{(k)} [/math]. |
In der Anwendung wählen wir einfach einen Startvektor, etwa einen Einheitsvektor und multiplizieren iterativ [math]H[/math] von links daran. Wir erhalten (unter geeigneten Startbedingungen) Konvergenz gegen einen Eigenvektor zum Eigenwert 1, denn es gibt hier keine größeren Eigenwerte als 1. Dieser stellt dann eine Lösung des LGS dar und enthält damit die gesuchten Page-Ranks.
Beispiel
Wir betrachten weiterhin das Beispiel aus dem Abschnitt Hyperlink-Übergangsmatrix mit der Matrix [math]H[/math] und wählen als Startvektor den folgenden Einheitsvektor:
[math]v=\begin{pmatrix} 1\\ 0\\ 0\\ 0\\ 0 \end{pmatrix}[/math]
Das bedeutet, dass wir bei Website [math]A[/math] starten. Nun multiplizieren wir die Matrix [math]H[/math] von links an den Vektor und erhalten
[math]H \cdot v=\begin{pmatrix} 0 & 0 & \frac{1}{3} & 0 & 0\\ \frac{1}{2} & 0 & \frac{1}{3} & 1 & \frac{1}{2}\\ 0 & \frac{1}{2} & 0 & 0 & 0\\ \frac{1}{2} & 0 & 0 & 0 & \frac{1}{2}\\ 0 & \frac{1}{2} & \frac{1}{3} & 0 & 0 \end{pmatrix}\cdot\begin{pmatrix} 1\\ 0\\ 0\\ 0\\ 0 \end{pmatrix}=\begin{pmatrix} 0\\ \frac{1}{2}\\ 0\\ \frac{1}{2}\\ 0 \end{pmatrix}[/math]
Multiplizieren wir die Matrix ausreichend oft erneut von links an den aktuellen Vektor, so erhalten wir folgenden Vektor:
[math]r\approx\begin{pmatrix} 0,061\\ 0,364\\ 0,182\\ 0,152\\ 0,242 \end{pmatrix}[/math]
Dies ist der Eigenvektor zum Eigenwert 1 unserer Matrix [math]H[/math]. Eine andere Möglichkeit zur Berechnung dieses Vektors ist, zunächst die Matrix ausreichend oft zu potenzieren und anschließend den Vektor [math]v[/math] von rechts zu multiplizieren. Das funktioniert, da gilt [math](H^i)v=H(\cdots (H(Hv))\cdots)[/math].
Markow-Ketten
Jetzt wollen wir eine schöne und intuitive Sichtweise dafür geben, was hier passiert. Das ist die Theorie der Markow-Ketten (hier sehr seicht abgehandelt!). Dabei geht es um eine Menge von Zuständen mit Übergangswahrscheinlichkeiten zwischen diesen. Hier stellt unsere Menge der Websites die Zustandsmenge dar und die Matrix [math]H[/math] die Übergangsmatrix. Die Interpretation ist die, dass ein zufälliger Surfer von einer beliebigen Website einen der Links zufällig anklickt und dann auf einer der anderen Websites landet. Das erklärt auch wieso sich die Spalten von [math]H[/math] zu 1 ergänzen sollten. Multipliziert man z. B. die Übergangsmatrix an den ersten Einheitsvektor, so erhält man die Wahrscheinlichkeiten, wo der zufällige Surfer sich nach einem Schritt befindet, wenn er auf der ersten Website gestartet ist.
Potenziert man diese Übergangsmatrix, etwa [math]H^k[/math], so erhält man in den Zellen die Übergangswahrscheinlichkeiten von einem Zustand (Spalte) zu einem anderen (Zeile) in genau [math]k[/math] Übergangsschritten. Das kann man sich leicht anhand der Matrixmultiplikation überlegen. Der Gedanke liegt nahe, dass diese Matrixpotenzen konvergieren, denn irgendwann spielen die Einzelübergänge keine große Rolle mehr; man erhält eine Matrix mit lauter gleichen Spalten (das kann man mit Matrixcalc sehr gut ausprobieren!). Das liegt daran, dass die Multiplikation mit jedem stochastischen Vektor (das ist ein Spaltenvektor mit nicht negativen Einträgen, die sich zu 1 ergänzen), wie etwa einem der Einheitsvektoren das gleiche ergibt: der Start spielt keine Rolle mehr, man erhält im Grenzwert eine Aufenthaltswahrscheinlichkeit für jeden der Zustände. Man spricht von der eindeutigen stationären Verteilung der Markow-Kette. Diese ist genau der PageRank! Sie ist also ein Maß dafür, wie viel Zeit der zufällige Surfer im stochastischen Sinn auf den einzelnen Websites verbringt und gibt somit Aufschluss über die wichtigsten Seiten.
Die oben beschriebene Konvergenz findet allerdings nur unter gewissen Voraussetzungen statt. Um diese soll es jetzt kurz gehen:
1. Voraussetzung
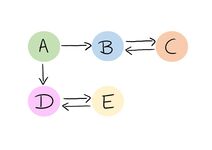
Es darf keine Seiten geben, die keine Links enthalten. Diese würden eine Sackgasse in der Markow-Kette darstellen; die Spalten müssen sich zu 1 addieren.
Beispiel
Wir sehen, dass zu der Website [math]C[/math] nur ein Pfeil hinführt, aber keiner mehr von [math]C[/math] weg zu einer anderen Website. Das heißt, auf [math]C[/math] ist keine andere Website verlinkt. Wenn wir dort landen, können wir uns nicht weiter durch Links durch das Internet klicken. Wir sind also in einer Sackgasse gelandet und die Ergebnisse der Ranks können mit der aktuellen Methode nicht berechnet werden.
2. Voraussetzung
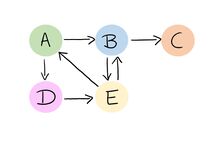
Es muss möglich sein, von jedem Zustand in jeden anderen Zustand zu gelangen (Irreduzibilität).
Beispiel
Wir erkennen, dass es zu einer Gruppenbildung kommt. Starten wir auf Website [math]A[/math], so gelangen wir entweder zu Website [math]B[/math] oder zu Website [math]D[/math]. Von [math]B[/math] kommen wir nur nach [math]C[/math]. Aber von beiden nicht mehr zurück nach [math]A[/math]. Das gleiche passiert uns, wenn wir uns von [math]A[/math] nach [math]D[/math] klicken. Das heißt, von jeder der beiden Gruppen gibt es keine Möglichkeit in die andere zu gelangen.
3. Voraussetzung
Es dürfen keine Probleme mit Zyklen auftreten, genauer: ab einem gewissen [math]k[/math] muss für alle [math]k'\gt k[/math] gelten dass [math]H^k[/math] nur Einträge größer Null besitzt, d. h. es ist möglich ist in genau [math]k'[/math] Schritten von jedem Zustand zu jedem anderen Zustand zu gelangen, egal wie klein die Wahrscheinlichkeit sein mag (ergodisch).
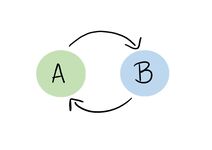
Beispiel
Hier liegen zwei Websites vor, die jeweils nur die andere verlinken. So kommt es dazu, dass wir langfristig immer zwischen den beiden hin- und herspringen und die Bedingung somit verletzt ist.
Verbesserungen - Der Dämpfungsfaktor
Damit der Algorithmus auch das richtige Ergebnis liefert, wenn eine oder mehrere der im vorherigen Abschnitt genannten Bedingungen verletzt sind, muss die Formel aus dem Abschnitt "Prinzip des PageRank-Algorithmus" noch um eine Komponente erweitert werden. Dafür wird der sogenannte Dämpfungsfaktor [math]d[/math] eingeführt, welcher Probleme dieser Art abfängt. Der Dämpfungsfaktor kann Werte zwischen 0 und 1 annehmen, standardmäßig wählt man [math]d=0,85[/math]. Sei nun [math]N[/math] die Anzahl der Websites in dem zu betrachtenden Internet. Damit gelangen wir zu folgender modifizierter Formel:
[math]R(a) = \frac{1-d}{N}+d\cdot\sum_{x \in B_a} \frac{R(x)}{L(x)} [/math]
Beispiel
Betrachten wir nun wieder unser Beispielinternet mit der Matrix [math]H[/math] und bilden die Matrix [math]H'[/math], welche den Dämpfungsfaktor berücksichtigt. Sei hierfür unser Dämpfungsfaktor [math]d=0,8[/math]. Wir fangen mit unser Matrix [math]H[/math] an.
[math]H=\begin{pmatrix} 0 & 0 & \frac{1}{3} & 0 & 0\\ \frac{1}{2} & 0 & \frac{1}{3} & 1 & \frac{1}{2}\\ 0 & \frac{1}{2} & 0 & 0 & 0\\ \frac{1}{2} & 0 & 0 & 0 & \frac{1}{2}\\ 0 & \frac{1}{2} & \frac{1}{3} & 0 & 0 \end{pmatrix}[/math]
Unser Internet besitzt fünf Websites, das heißt, [math]N=5[/math]. Daraus folgt: [math]\frac{1-d}{N}=\frac{1-0,8}{5}=\frac{1}{25}[/math].
Nun müssen wir zunächst unsere Matrix [math]H[/math] mit dem Dämpfungsfaktor [math]d[/math] multiplizieren. Das heißt, jeder einzelne Eintrag wird mit [math]d=0.8=\frac{4}{5}[/math] multipliziert und wir erhalten:
[math]d\cdot H=\begin{pmatrix} 0 & 0 & \frac{4}{5}\cdot\frac{1}{3} & 0 & 0\\ \frac{4}{5}\cdot\frac{1}{2} & 0 & \frac{4}{5}\cdot\frac{1}{3} & \frac{4}{5}\cdot 1 & \frac{4}{5}\cdot\frac{1}{2}\\ 0 & \frac{4}{5}\cdot\frac{1}{2} & 0 & 0 & 0\\ \frac{4}{5}\cdot\frac{1}{2} & 0 & 0 & 0 & \frac{4}{5}\cdot\frac{1}{2}\\ 0 & \frac{4}{5}\cdot\frac{1}{2} & \frac{4}{5}\cdot\frac{1}{3} & 0 & 0 \end{pmatrix}=\begin{pmatrix} 0 & 0 & \frac{4}{15} & 0 & 0\\ \frac{2}{5} & 0 & \frac{4}{15} & \frac{4}{5} & \frac{2}{5}\\ 0 & \frac{2}{5} & 0 & 0 & 0\\ \frac{2}{5} & 0 & 0 & 0 & \frac{2}{5}\\ 0 & \frac{2}{5} & \frac{4}{15} & 0 & 0 \end{pmatrix}[/math]
Addieren wir nun auf jeden Eintrag [math]\frac{1-d}{N}=\frac{1}{25}[/math], so erhalten wir:
[math]H'=\frac{1}{25}\begin{pmatrix} 1 & 1 & \frac{23}{3} & 1 & 1\\ 11 & 1 & \frac{23}{3} & 21 & 11\\ 1 & 11 & 1 & 1 & 1\\ 11 & 1 & 1 & 1 & 11\\ 1 & 11 & \frac{23}{3} & 1 & 1 \end{pmatrix}[/math]
Wir sehen, dass die Summe aller Einträge in einer Spalte immer noch eins ergibt. Allerdings hat die Matrix [math]H'[/math] keine einzige 0 mehr als Eintrag, insbesondere auch nicht auf der Diagonalen (Websites verweisen jetzt auch auf sich selbst). Das heißt, dass es möglich ist, von jeder Website auf jede andere zu kommen. Es gibt also keine Sackgassen mehr, es können sich keine Gruppen bilden und erreicht man eine Website in [math]k[/math] Schritten, so erreicht man sie sicherlich auch in [math]k' (k'\gt k)[/math] Schritten. Genau das, was wir mit dem Dämpfungsfaktor erreichen wollten!
Der Dämpfungsfaktor schafft also erst Platz, indem wir die Matrix mit [math]d[/math] multiplizieren, sodass wir dann überall noch [math]\frac{1-d}{N}[/math] addieren können, ohne die Summe 1 (also 100%) zu überschreiten. Somit werden jegliche Verletzungen der drei Voraussetzungen aufgefangen, ohne, dass das eigentliche Ergebnis zu sehr verfälscht wird.
Quellen und weiterführende Links
- https://homepage.univie.ac.at/Franz.Embacher/Lehre/aussermathAnw/Google.html
- https://en.wikipedia.org/wiki/PageRank
- https://de.wikipedia.org/wiki/Google-Matrix
- Arens, T. (et al.): Mathematik, Springer 2008
Autoren
Mathis, Julia