Mandelbrotmenge: Unterschied zwischen den Versionen
Selin (Diskussion | Beiträge) |
Selin (Diskussion | Beiträge) |
||
| (71 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | <h1>Julia-Mengen</h1> | |
| − | < | + | <h2>Hintergrund </h2> |
| + | Julia-Mengen sind einer der am meist abgebildeten Fraktale, die auf elegante Weise Ästhetik und Mathematik vereint. Sie sind eine Teilmengen der komplexen Zahlenebene. Erstmals 1918 wurden Julia-Mengen vom Mathematiker Gaston Maurice Julia in seinem Werk "Memoire sur l'iteration des functions rationelles" <ref>[https://www.emis.de/journals/AMEN/posters/poster0171.pdf], (übersetztes) Werk von Julia</ref> behandelt. | ||
| − | + | Der Hintergrund dieser Arbeit war die Untersuchung über die globale Dynamik des Newton-Verfahrens, die erstmal 1879 von Arthur Cayley von den reellen Zahlen auf die komplexe Ebene ausgedehnt wurde. Caylay studierte den Fall eines kubischen Polynoms <math> f(z) = z^3 + 0 | |
| − | |||
| − | |||
| − | |||
</math>, indem er versuchte mithilfe der Newton–Fourier Methode die Nullstellen von <math> f | </math>, indem er versuchte mithilfe der Newton–Fourier Methode die Nullstellen von <math> f | ||
| − | </math> zu finden. Da es in der komplexen Zahlenebene hier drei Lösungen gibt, war Cayleys Ziel eine allgemeine Methode zu finden, die bestimmt gegen welche Wurzel die Iteration für einen gegebenen Startwert <math> z </math> konvergiert. | + | </math> zu finden. Da es in der komplexen Zahlenebene hier drei Lösungen gibt, war Cayleys Ziel ,eine allgemeine Methode zu finden, die bestimmt, gegen welche Wurzel die Iteration für einen gegebenen Startwert <math> z </math> konvergiert. |
| − | Da jegliche Anstrengungen Cayleys und anderer Mathematiker keine Resultate zeigten, wurde die Arbeit die darauffolgenden Jahre eingestellt. Erst zu beginn des 20. Jahrhunderts, als von der Französischen Akademie für Naturwissenschaften ein Preis | + | Da jegliche Anstrengungen Cayleys und anderer Mathematiker keine Resultate zeigten, wurde die Arbeit die darauffolgenden Jahre eingestellt. Erst zu beginn des 20. Jahrhunderts, als von der Französischen Akademie für Naturwissenschaften ein Preis angekündigt wurde, nahmen zahlreiche Mathematiker die Arbeit erneut auf. Die Mathematiker, die erfolgreiche Resultate hervorbrachten, waren Pierre Fatou und Gaston Julia, die mit ihrer entwickelten Theorie der Iterationen rationaler Funktionen in der komplexen Ebene das Problem lösten. |
| − | Julia lieferte hierbei eine konkrete Beschreibung von komplexwertigen Mengen, für deren Punkte die Orbits bei Anwendung auf eine rationale Funktion beschränkt bleiben und gewann den ersten Preis. Fatou, der ähnliche Ideen wie Julia in seiner Arbeit vorstellte, erhielt den zweiten Preis. | + | Julia lieferte hierbei eine konkrete Beschreibung von komplexwertigen Mengen, für deren Punkte die Orbits bei Anwendung auf eine rationale Funktion beschränkt bleiben und gewann den ersten Preis. Fatou, der ähnliche Ideen wie Julia in seiner Arbeit vorstellte, erhielt den zweiten Preis. |
| − | In den nächsten Jahren wuchs das Interesse an diesem Thema sehr stark an und zahlreiche bekannte Mathematiker wie Harald Cramer widmeten ihre Aufmerksamkeit der Julia-Mengen. | + | In den nächsten Jahren wuchs das Interesse an diesem Thema sehr stark an und zahlreiche bekannte Mathematiker wie Harald Cramer widmeten ihre Aufmerksamkeit der Julia-Mengen. Doch aufgrund der fehlenden Möglichkeiten Rechenmaschinen für die aufwendigen Berechnung zu benutzen, gerieten auch die Julia-Mengen mit den Jahre in Vergessenheit. |
| − | Erst 1977 | + | Erst 1977 gelang es dem französische Mathematiker Benoit Mandelbrot mithilfe von Computergrafik die Schönheit der Julia-Mengen visualisieren. |
| − | <h2>Definition | + | <h2>Definition </h2> |
| − | Sei <math>f</math> eine auf ganz <math>\mathbb{C}</math> meromorphe Funktion. Des Weiteren sei <math>\mathrm{grad}(f) > 1</math>. Definiere für ein <math>z \in \hat{\mathbb{C}} := \mathbb{C} \cup \{\infty\}</math> den dynamischen Prozess \begin{align*} | + | Sei <math>f</math> eine auf ganz <math>\mathbb{C}</math> [https://de.wikipedia.org/wiki/Meromorphe_Funktion meromorphe] Funktion. Des Weiteren sei <math>\mathrm{grad}(f) > 1</math>. Definiere für ein <math>z \in \hat{\mathbb{C}} := \mathbb{C} \cup \{\infty\}</math> den dynamischen Prozess \begin{align*} |
| − | z \mapsto f( | + | z \mapsto f(z) |
\end{align*} wodurch ausgehend von einem Startpunkt <math>z_0 \in \hat{\mathbb{C}}</math> die Rekursion \begin{align*} | \end{align*} wodurch ausgehend von einem Startpunkt <math>z_0 \in \hat{\mathbb{C}}</math> die Rekursion \begin{align*} | ||
| − | + | z_{n+1} = f(z_n), \qquad n \in \mathbb{N}_0. | |
\end{align*} | \end{align*} | ||
ensteht. Dadurch erhält man die Folge <math>z_0 \mapsto f(z_0) =: f^1(z_0) \mapsto f(f(z_0)) =: f^2(z_0)\mapsto \cdots</math> von komplexen Zahlen, wobei hier mit <math>f^n, n \in \mathbb{N}</math> , die n-malige Hintereinanderausführung von <math>f</math> gemeint ist. Die Folge <math>f^n(z_0)</math> weist nun zwei grundlegende Verschiedenheiten auf: | ensteht. Dadurch erhält man die Folge <math>z_0 \mapsto f(z_0) =: f^1(z_0) \mapsto f(f(z_0)) =: f^2(z_0)\mapsto \cdots</math> von komplexen Zahlen, wobei hier mit <math>f^n, n \in \mathbb{N}</math> , die n-malige Hintereinanderausführung von <math>f</math> gemeint ist. Die Folge <math>f^n(z_0)</math> weist nun zwei grundlegende Verschiedenheiten auf: | ||
| Zeile 28: | Zeile 26: | ||
<li>Die Iteration führt unter dem Startwert <math>z_0</math> zu einer instabilen Dynamik. D.h. <math>|f^n(z_0)|</math> bleibt beschränkt für steigende <math>n</math>. Solche Startwerte werden dann der <b>Julia-Menge</b> zugeordnet. Die Julia-Menge zu einer gegebenen Funktion <math>f</math> wird mit <b><math>J(f)</math></b> abgekürzt.</li> | <li>Die Iteration führt unter dem Startwert <math>z_0</math> zu einer instabilen Dynamik. D.h. <math>|f^n(z_0)|</math> bleibt beschränkt für steigende <math>n</math>. Solche Startwerte werden dann der <b>Julia-Menge</b> zugeordnet. Die Julia-Menge zu einer gegebenen Funktion <math>f</math> wird mit <b><math>J(f)</math></b> abgekürzt.</li> | ||
</ul> | </ul> | ||
| − | Man sieht sofort dass <math>J(f) = \mathbb{C} | + | Man sieht sofort, dass <math>J(f) = \mathbb{C}\setminus F(f) = F(f)^c</math> und somit <math>J(f) \cup F(f) = \mathbb{C}</math>. |
Aufgrund dieser Eigenschaft wird sich in diesem Artikel aussließlich auf die Julia-Menge bezogen. | Aufgrund dieser Eigenschaft wird sich in diesem Artikel aussließlich auf die Julia-Menge bezogen. | ||
| − | Eine | + | Eine Definition der Julia-Menge geschieht über den Abschluss ihrer abstoßenden periodischen Punkte in Abhängigkeit von der gegebenen Funktion <math>f</math>. Ein Punkt <math>z_0</math> heißt periodisch falls es ein <math>n \in \mathbb{N}</math> gibt, sodass <math>z_0 = z_n</math> gilt. Ein periodischer Punkt <math>z_0</math> heißt abstoßend, falls <math>|(f^n)'(z_0)| > 1</math><nowiki> gilt. Formal setzt man also |
| − | J(f) = \partial\left\{z \in \mathbb{C} | \lim\limits_{t \rightarrow \infty} |f^t(z)|<\infty \right\} | + | \begin{align*} |
| − | \end{align*} | + | J(f) = \overline{\left\{z \in \mathbb{C} \big| z\ \text{ist abstoßender periodischer Punkt} \right\}}. |
| − | <h2>Grundlegende Eigenschaften | + | \end{align*} |
| + | Für Polynome mit einem Grad </nowiki><math>\geq 2</math><nowiki> kann die Definition vereinfacht werden zu \begin{align*} | ||
| + | J(f) = \partial\left\{z \in \hat{\mathbb{C}} \big| \lim\limits_{t \rightarrow \infty} |f^t(z)|<\infty \right\}. | ||
| + | \end{align*}</nowiki> | ||
| + | <h2>Grundlegende Eigenschaften </h2> | ||
| + | |||
| + | '''Julia-Mengen können sowohl zusammenhängend als auch nicht zusammenhängend sein.''' | ||
| + | |||
| + | 2. <math> J(f_c)</math> und <math>J(f_ c¯) </math> liegen symmetrisch zur imaginären Achse. | ||
| + | |||
| + | '''Chaotisch:''' | ||
| + | |||
| + | Sei <math> f</math> ein Polynom vom Grad ≥ 2 mit der Julia-Menge. Dann ist <math> f</math> auf der Julia-Menge chaotisch. | ||
| + | |||
| + | Auffällig ist auch, dass es bereits bei kleinen Änderungen von z, zu einem anderen Verhalten kommt. | ||
| + | |||
| + | '''Julia-Menge eines beliebigen Polynoms:''' | ||
| + | |||
| + | Die Julia-Menge eines Polynoms <math>f </math> vom Grad ≥ 2 ist nichtleer und kompakt. | ||
| + | <h2>Julia-Mengen von quadratischen Polynomen </h2> | ||
| + | Julia-Mengen von quadratischen Polynomen sind besonders interessant. | ||
| + | |||
| + | Man nehme beispielsweise: | ||
| + | |||
| + | <math> f_c: ℂ → ℂ</math> | ||
| − | + | <math> z → z^2+c</math> | |
| − | + | Wenn man nun für c=0 einsetzt, kommt man auf folgendes: | |
| − | + | <math> f(z)=z^2+c</math> | |
| − | + | '''Hier gilt:''' | |
| − | + | <math> f(z)=z^2</math> | |
| − | + | K(f) = { z| |z| ≤ 1 } und J(f) = {z ∈ ℂ| |z| = 1 } | |
| + | Zu erwähnen sei auch, dass <math> f_c</math> für c = 0 als Julia-Menge den Einheitskreis besitzt.[[Datei:Einheitskreis.jpg|ohne|mini|Julia-Menge für c = 0|verweis=https://funfacts.mathi.uni-heidelberg.de/index.php/Datei:Einheitskreis.jpg]]Setzt man jetzt für c andere Werte ein, verändert sich die Julia-Menge. | ||
| + | {| class="wikitable" | ||
| + | |1 | ||
| + | |<math> f(z)=z^2+1</math> | ||
| + | |<math> z_0 = 0 : f_1(z_0) = 1 </math> | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | |<math> f_1 ²(0)=2</math> | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | |<math> f_1 ³ (0)= 5</math> | ||
| + | |- | ||
| + | | -1 | ||
| + | |<math> f(z)=z^2-1</math> | ||
| + | |<math> z_0 = 0 : f_{-1}(z_0) = - 1 </math> | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | |<math> f_{-1} ²(0)=2</math> | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | |<math> f_{-1} ²(0)=-5</math> | ||
| + | |}Um die Veränderung der Julia- Mengen in Zusammenhang mit anderen c- Werten besser nachzuvollziehen, kann man sich dieses Bild anschauen:[[Datei:Julia-Teppich.png|mini|verweis=https://funfacts.mathi.uni-heidelberg.de/index.php/Datei:Julia-Teppich.png|alternativtext=|ohne]][https://commons.wikimedia.org/wiki/File:Julia-Teppich.png] | ||
| − | + | Hier kann man nochmal genau sehen, wie aus dem Einheitskreis bei c=0, bei veränderten c- Werten wie beispielsweise c=-0.4 c=-0.8 und c=-1, andere kreisförmige Körper entstehen. | |
| − | + | '''Symmetrie:''' | |
| − | + | Für die Julia-Menge <math> J(f_c)</math> von <math>f_{n+1}(z)=z_n^2+c</math> gilt: | |
| − | + | 1. <math> J(f_c)</math> ist punktsymmetrisch zum Ursprung: <math>z \in\ J(f_c) ⇔ -z \in\ J(f_c)</math> | |
| + | {| class="wikitable" | ||
| + | |+ | ||
| + | !''Beweis.'' | ||
| + | !<math> f_{n+1}(-z)=(-z)^2+c=f_{n+1}(z) , | ||
| − | |||
| − | + | </math> | |
| + | |- | ||
| + | ! | ||
| + | !<math> (f_{n+1})^k(-z)=(f_{n+1})^{n-1}(f_{n+1}(-z))=(f_{n+1})^{n-1} (f_{n+1}(z))=(f_{n+1})^k(z)</math> | ||
| + | |} | ||
| − | + | 2. <math> J(f_c)</math> und ''<math>J(f_ \overline {c}) </math>'' liegen symmetrisch zur imaginären Achse.<h2>Graphische Darstellung </h2> | |
| − | <h2>Graphische Darstellung | + | [[Datei:Julia1.png|200px|thumb|Julia-Menge mit c=-0.6+0.6i erzeugt durch den nebenstehenden Code|alternativtext=]] [[Datei:Julia2.png|200px|thumb|Julia-Menge mit c=-0.8+0.4i erzeugt durch den nebenstehenden Code|alternativtext=]] |
| − | Zur graphischen Darstellung von Julia-Mengen von einem ausgehenden Startwert <math> | + | Zur graphischen Darstellung von Julia-Mengen von einem ausgehenden Startwert <math> z_0 \in \mathbb{C}</math> wird eine Farbe eines Punktes danach gewählt, wie viele Iterationen notwendig waren, bis <math>|z_n| \geq m \geq 2</math> (<math>m \in \mathbb{N}</math> beliebig), da im Allgemeinen die Iterationen für alle <math>z_0</math> mit <math>|z_0| \geq 2</math> divergieren. Die Wahl von <math>m= 2</math> ist grundsätzlich möglich, jedoch werden bei einer größeren Wahl von <math>m</math> (z.B.<math>m=1000</math>) qualitativ hochwertigere Bilder ausgegeben . Ist nach einer vorgegebene Iterationszahl <math>n</math> ein Punkt betragsmäßig kleiner als <math>m</math> so wird angenommen, dass der Punkt konvergiert. Diese Punkte werden in der Regel dunkel gefärbt, dementsprechend werden Punkte die schneller Konvergieren heller gefärbt. Der nachfolgende Python-Code<ref>Daschaew, Mansur. (2021, März 15)</ref> stellt für einen gegebenen Punkt <math>c</math> nach <math>n</math> Iterationen die gewünschte Julia-Menge dar. |
<pre> | <pre> | ||
import numpy as np | import numpy as np | ||
| Zeile 103: | Zeile 158: | ||
plt.imsave(my_path + name, J, cmap=cmap, origin="lower") | plt.imsave(my_path + name, J, cmap=cmap, origin="lower") | ||
</pre> | </pre> | ||
| − | Hierbei wird als | + | Hierbei wird als Funktionen <math>f</math> ein Polynom zweiten Grades gewählt, also <math>f=z^2+c</math>. Das Paket <code>numpy</code> wird verwendet um die nötigen Berechnungen effizient in vektorisierter Form zu lösen anstatt diese aufwendig mithilfe von Schleifen zu berechnen. |
<h1>Mandelbrot-Menge</h1> | <h1>Mandelbrot-Menge</h1> | ||
| − | <h2>Definition über die Julia-Mengen | + | <h2>Definition über die Julia-Mengen </h2> |
Die Mandelbrotmenge wurde zur Klassifizierung der Julia-Mengen definiert. Sie umfasst die Teilmenge der komplexen Zahlen, für welche die Julia Menge zusammenhängend ist. | Die Mandelbrotmenge wurde zur Klassifizierung der Julia-Mengen definiert. Sie umfasst die Teilmenge der komplexen Zahlen, für welche die Julia Menge zusammenhängend ist. | ||
Die Mandelbrotmenge lässt sich rekursiv, wie folgt definieren: | Die Mandelbrotmenge lässt sich rekursiv, wie folgt definieren: | ||
| − | ::<math> z_{n+1}=z_n^2+c </math> mit <math>z_0 = 0 </math> | + | ::<math> M=\{c\in \mathbb{C}\mid z_{n+1}=z_n^2+c \text{ bleibt beschränkt } \forall n\in \mathbb{N} </math> mit <math>z_0 = 0 </math> |
| − | Um nun für bestimmte Werte <math>c\in\mathbb{C}</math> zu bestimmen, ob sie in der Mandelbrotmenge enthalten sind | + | Um nun für bestimmte Werte <math>c\in\mathbb{C}</math> zu bestimmen, ob sie in der Mandelbrotmenge enthalten sind, führt man <math>n\in\mathbb{N}</math> Iterationen durch. Wenn gilt |
| − | <math>\mid f^n_c(0)\mid > 2</math>, so färbt man den entsprechenden Punkt weiß, er liegt also nicht in <math>M</math>. Ansonsten färbt | + | <math>\mid f^n_c(0)\mid > 2</math>, so färbt man den entsprechenden Punkt weiß, er liegt also nicht in <math>M</math>. Ansonsten färbt man ihn schwarz. Desto größer <math>n</math> gewählt wird, desto genauer wird das Bild, dass man erhält. In der Mathematik sind theoretisch beliebige Genauigkeiten möglich, dies führt zu den faszinierenden graphischen Darstellungen der Mandelbrotmenge, wenn man weiter reinzoomt. |
Abhängig von der Definition der Juliamenge lässt sich die Mandelbrotmenge, wie folgt definieren: | Abhängig von der Definition der Juliamenge lässt sich die Mandelbrotmenge, wie folgt definieren: | ||
| − | ::<math>M=\{c\in \mathbb{C}\mid | + | ::<math>M=\{c\in \mathbb{C}\mid J(f) \text{ ist zusammenhängend}\}</math> |
Weitere Definitionen der Mengen sind: | Weitere Definitionen der Mengen sind: | ||
::<math> M=\{c\in\mathbb{C}\mid f^n_c(0)\not\to\infty\text{, wenn } n\to \infty\}=\{c\in\mathbb{C}\mid (z_n)_{n\in\mathbb{N}} \text{ ist beschränkt}\}</math> | ::<math> M=\{c\in\mathbb{C}\mid f^n_c(0)\not\to\infty\text{, wenn } n\to \infty\}=\{c\in\mathbb{C}\mid (z_n)_{n\in\mathbb{N}} \text{ ist beschränkt}\}</math> | ||
Diese Darstellungen lassen sich mithilfe der oberen Definition beweisen.<ref>[http://www.mathematik.uni-ulm.de/stochastik/lehre/ws06_07/seminar_fraktale/ausarbeitung_voelkel.pdf], weiterführender Beweis zur Mengendarstellung</ref> | Diese Darstellungen lassen sich mithilfe der oberen Definition beweisen.<ref>[http://www.mathematik.uni-ulm.de/stochastik/lehre/ws06_07/seminar_fraktale/ausarbeitung_voelkel.pdf], weiterführender Beweis zur Mengendarstellung</ref> | ||
| − | <h2>Grundlegende Eigenschaften | + | <h2>Grundlegende Eigenschaften </h2> |
<h3>Grenzverhalten ausgewählter Funktionen</h3> | <h3>Grenzverhalten ausgewählter Funktionen</h3> | ||
Für verschiedene Punkte <math>c\in\mathbb{C}</math> lassen sich vier verschiedene Grenzverhalten beobachten: | Für verschiedene Punkte <math>c\in\mathbb{C}</math> lassen sich vier verschiedene Grenzverhalten beobachten: | ||
| Zeile 127: | Zeile 182: | ||
::*chaotisches aber beschränktes Verhalten der Glieder | ::*chaotisches aber beschränktes Verhalten der Glieder | ||
::*Divergenz gegen unendlich | ::*Divergenz gegen unendlich | ||
| − | Ein Punkt <math>c\in\mathbb{C}</math> ist in <math>M</math> falls er eines der | + | Ein Punkt <math>c\in\mathbb{C}</math> ist in <math>M</math> falls er eines der ersten drei Grenzverhalten aufzeigt. |
{| class="sortable" | {| class="sortable" | ||
|+ Betrachten wir das Grenzverhalten der Funktion <math>z_{n+1}=z_n^2+c</math> | |+ Betrachten wir das Grenzverhalten der Funktion <math>z_{n+1}=z_n^2+c</math> | ||
| Zeile 145: | Zeile 200: | ||
| -2 || 2, 2, 2,... || Konvergenz gegen 2 || <math>2\in M</math> | | -2 || 2, 2, 2,... || Konvergenz gegen 2 || <math>2\in M</math> | ||
|- | |- | ||
| − | | 0,25 || <math> \frac{5}{16}</math>, <math> \frac{89}{256}</math>, <math> \frac{24305}{65536}</math>,... || | + | | 0,25 || <math> \frac{5}{16}</math>, <math> \frac{89}{256}</math>, <math> \frac{24305}{65536}</math>,... || Konvergenz gegen 0,5 || <math>0,25\in M</math> |
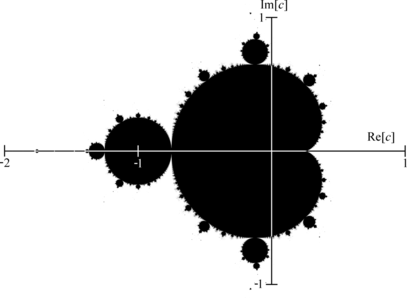
| − | |} | + | |}[[Datei:Mandelbrotmenge.png|mini|407x407px|Von Connelly (Diskussion · Beiträge), Gemeinfrei, <nowiki>https://commons.wikimedia.org/w/index.php?curid=16088</nowiki>]] |
<h3>M ist kompakt</h3> | <h3>M ist kompakt</h3> | ||
Die Mandelbrotmenge ist abgeschlossen, da ihr Komplement offen ist. Außerdem liegt sie innerhalb eines Kreises um den Ursprung mit Radius 2, daraus folgt Beschränktheit.<blockquote> | Die Mandelbrotmenge ist abgeschlossen, da ihr Komplement offen ist. Außerdem liegt sie innerhalb eines Kreises um den Ursprung mit Radius 2, daraus folgt Beschränktheit.<blockquote> | ||
<math>M\subset B_2(0)\subset \mathbb{C}</math> | <math>M\subset B_2(0)\subset \mathbb{C}</math> | ||
</blockquote>Nach dem Satz von Heine-Borel folgt somit Kompaktheit. | </blockquote>Nach dem Satz von Heine-Borel folgt somit Kompaktheit. | ||
| − | <h3>M ist spiegelsymmetrisch zur | + | <h3>M ist spiegelsymmetrisch zur reellen Achse</h3> |
| − | Diese Tatsache lässt sich leicht anhand der Bilder erkennen. Doch auch bei Betrachtung der mathematischen Grundlagen kann dieser Umstand leicht gezeigt werden. Wir wollen also zeigen, dass wenn <math>a+bi= | + | Diese Tatsache lässt sich leicht anhand der Bilder erkennen. Doch auch bei Betrachtung der mathematischen Grundlagen kann dieser Umstand leicht gezeigt werden. Wir wollen also zeigen, dass wenn <math>a+bi=c\in M</math> ist, auch <math>a-bi=\overline c \in M</math> ist. |
| + | |||
{| class="wikitable" | {| class="wikitable" | ||
|+ Betrachten wir die Entwicklung der rekursiven Gleichung mit <math>c_1</math> und <math>\overline c_1</math> | |+ Betrachten wir die Entwicklung der rekursiven Gleichung mit <math>c_1</math> und <math>\overline c_1</math> | ||
|- | |- | ||
| − | ! <math> | + | ! <math>n</math> !! <math>z_{n+1}=z_{n}+c</math> !! <math>z_{n+1}=z_{n}+\overline c</math> |
| + | |- | ||
| + | | 1 || <math>0+a+bi</math> || <math>0+a-bi</math> | ||
|- | |- | ||
| − | | | + | | 2 || <math>(a+bi)^2+a+bi=(a^2-b^2+a)+i(b+2ab)</math> || <math>(a-bi)^2+a-bi=(a^2-b^2+a)-i(b+2ab)</math> |
|- | |- | ||
| − | | | + | | 3 || <math>((a^2-b^2+a)+i(b+2ab))^2 + a + bi \\= (a^2-b^2+a)^2-(b+2ab)^2+a+i(2((a^2-b^2+a)(b+2ab)+b)) </math> || <math>((a^2-b^2+a)-i(b+2ab))^2 + a - bi |
| + | \\= (a^2-b^2+a)^2-(b+2ab)^2+a-i(2((a^2-b^2+a)(b+2ab)+b)) </math> | ||
|- | |- | ||
| − | | | + | | n || <math> Re(z_n)+i*Im(z_n)</math> || <math> Re(z_n)-i*Im(z_n)</math> |
|} | |} | ||
| − | Wir sehen hier, dass <math>z_n+ | + | Wir sehen hier, dass für <math>z_{n+1}=z_n+c</math> und <math>\overline{z_{n+1}}=z_n+\overline c</math> gilt: <math>Re(z_n)=Re(\overline z_n) </math> und <math>Im(z_n)=Im(\overline z_n) </math> . Die Beträge sind also identisch und Realteil und Imaginärteil entsprechen einander. Daraus lässt sich folgern, wenn ein Werte nicht gegen unendlich divergiert, so auch nicht sein komplex konjugierter Wert. Somit ergibt sich: |
| + | |||
| + | <math>a+bi=c_1\in M\rightarrow a-bi=\overline c_1 \in M</math> | ||
| + | |||
| + | Also entsteht ein achsensymmetrisches Bild. | ||
<h3>M ist zusammenhängend</h3> | <h3>M ist zusammenhängend</h3> | ||
Diese Tatsache wurde 1984 von Adrien Douady und John Hamal Hubbard bewiesen. Ob sie auch lokal zusammenhängend ist, ist noch eine offene Frage. | Diese Tatsache wurde 1984 von Adrien Douady und John Hamal Hubbard bewiesen. Ob sie auch lokal zusammenhängend ist, ist noch eine offene Frage. | ||
| − | <h2>Graphische Darstellung | + | <h2>Graphische Darstellung</h2> |
Es gibt verschiedene farbliche Visualisierungen der Mandelbrotmenge, aber nach Konvention sind alle Punkte, die zur Mandelbrotmenge dazugehören, schwarz eingezeichnet, d.h. alle <math>c</math>, für die die Folge <math>z_{n}</math> beschränkt bleibt. Die sich so ergebende Menge wird auch als »Apfelmännchen« bezeichnet, was sich einem erschließt, wenn man den Kopf um 90 Grad nach links neigt. Bei näherer Betrachtung der Mandelbrotmenge erkennt man, dass sich die Struktur des Apfelmännchens am Rand der Menge in kleinerer Ausführung wiederholt. | Es gibt verschiedene farbliche Visualisierungen der Mandelbrotmenge, aber nach Konvention sind alle Punkte, die zur Mandelbrotmenge dazugehören, schwarz eingezeichnet, d.h. alle <math>c</math>, für die die Folge <math>z_{n}</math> beschränkt bleibt. Die sich so ergebende Menge wird auch als »Apfelmännchen« bezeichnet, was sich einem erschließt, wenn man den Kopf um 90 Grad nach links neigt. Bei näherer Betrachtung der Mandelbrotmenge erkennt man, dass sich die Struktur des Apfelmännchens am Rand der Menge in kleinerer Ausführung wiederholt. | ||
| Zeile 175: | Zeile 238: | ||
Auf [https://www.geogebra.org/m/BUVhcRSv#material/XQprvGbW Geogebra] hat man die Möglichkeit, sich das Konvergenz- bzw. Divergenzverhalten der Folge <math>z_{n}</math> für verschiedene <math>c</math> darstellen zu lassen. Zudem werden durch Schraffieren auf der komplexen Ebene alle zur Mandelbrotmenge zugehörigen Punkte sichtbar. Allerdings treten bei dem Programm Rundungsfehler auf, z.B. scheint bei Geogebra die Folge für <math>c=i</math> zu divergieren, obwohl man berechnen kann, dass sie für <math>i</math> beschränkt bleibt. | Auf [https://www.geogebra.org/m/BUVhcRSv#material/XQprvGbW Geogebra] hat man die Möglichkeit, sich das Konvergenz- bzw. Divergenzverhalten der Folge <math>z_{n}</math> für verschiedene <math>c</math> darstellen zu lassen. Zudem werden durch Schraffieren auf der komplexen Ebene alle zur Mandelbrotmenge zugehörigen Punkte sichtbar. Allerdings treten bei dem Programm Rundungsfehler auf, z.B. scheint bei Geogebra die Folge für <math>c=i</math> zu divergieren, obwohl man berechnen kann, dass sie für <math>i</math> beschränkt bleibt. | ||
| − | <h2>Geschichte | + | <h2>Geschichte </h2>Fraktale waren schon lange vor dem französischen Mathematiker Benoît B. Mandelbrot (1924-2010) ein untersuchtes Teilgebiet der Mathematik. So veröffentlichte der schwedische Mathematiker Helge von Koch (1870-1924) seine berühmte Koch-Kurve (auch »Schneeflockenkurve«) bereits 1904 – noch früher, im Jahr 1890, stellte der italienische Mathematiker Guiseppe Peano (1858-1932) die Peano-Kurve vor. Beides sind Beispiele für Fraktale, aber erst 1975 gab Mandelbrot solchen Gebilden schließlich einen Namen (abgeleitet aus dem Lateinischen »fractus« = gebrochen), weshalb er auch »Vater der Fraktale« genannt wird. |
1967 befasste er sich mit der Frage, wie man die Länge von Großbritanniens Küste, ebenfalls einem Fraktal, messen könne. Dabei stieß Mandelbrot auf das Problem, unterschiedliche Ergebnisse zu bekommen, je nachdem wie genau er vorging und wie stark er manche feinere Ausbuchtungen bei der Messung vereinfacht nur als glatte Kurve einberechnete. | 1967 befasste er sich mit der Frage, wie man die Länge von Großbritanniens Küste, ebenfalls einem Fraktal, messen könne. Dabei stieß Mandelbrot auf das Problem, unterschiedliche Ergebnisse zu bekommen, je nachdem wie genau er vorging und wie stark er manche feinere Ausbuchtungen bei der Messung vereinfacht nur als glatte Kurve einberechnete. | ||
1980 veröffentlichte er schließlich seine Arbeit über die Mandelbrotmenge, deren Ursprung in den Julia-Mengen liegt, die schon 1905 von Gaston Maurice Julia und Pierre Fatou untersucht wurden. Schon zwei Jahre vor dieser Veröffentlichung gab es erste graphische Darstellungen der Mandelbrotmenge am Computer. | 1980 veröffentlichte er schließlich seine Arbeit über die Mandelbrotmenge, deren Ursprung in den Julia-Mengen liegt, die schon 1905 von Gaston Maurice Julia und Pierre Fatou untersucht wurden. Schon zwei Jahre vor dieser Veröffentlichung gab es erste graphische Darstellungen der Mandelbrotmenge am Computer. | ||
| − | + | ||
| − | --> | + | <h2>Weblinks</h2> |
| + | https://www.youtube.com/watch?v=lO1B2uA4l38 -Eine Dokumentation über Fraktale, die unter anderem auch den kommerziellen Erfolg der Mandelbrot-Menge zeigt | ||
| + | |||
| + | <h2>Einzelnachweise</h2> | ||
<references /> | <references /> | ||
| + | <references group="Quelle: Dufner, J.; Roser, A.; Unseld, F. (Hrsg.) 1998, Fraktale und Julia-Mengen, 1. Auflage, Frankfurt am Main." /> | ||
| + | <references group="Quelle: G. M. Julia; 1918, Memoir on iterations of rational functions übersetzt von A. Rosa, 2001" /> | ||
| + | |||
| + | <h2>Autoren</h2> | ||
| + | * Mansur Daschaew | ||
| + | * Hannah Otte | ||
| + | * Selin Koparan | ||
| + | * Danielle Eitelmann | ||
Aktuelle Version vom 12. April 2021, 14:17 Uhr
Julia-Mengen
Hintergrund
Julia-Mengen sind einer der am meist abgebildeten Fraktale, die auf elegante Weise Ästhetik und Mathematik vereint. Sie sind eine Teilmengen der komplexen Zahlenebene. Erstmals 1918 wurden Julia-Mengen vom Mathematiker Gaston Maurice Julia in seinem Werk "Memoire sur l'iteration des functions rationelles" [1] behandelt.
Der Hintergrund dieser Arbeit war die Untersuchung über die globale Dynamik des Newton-Verfahrens, die erstmal 1879 von Arthur Cayley von den reellen Zahlen auf die komplexe Ebene ausgedehnt wurde. Caylay studierte den Fall eines kubischen Polynoms [math] f(z) = z^3 + 0 [/math], indem er versuchte mithilfe der Newton–Fourier Methode die Nullstellen von [math] f [/math] zu finden. Da es in der komplexen Zahlenebene hier drei Lösungen gibt, war Cayleys Ziel ,eine allgemeine Methode zu finden, die bestimmt, gegen welche Wurzel die Iteration für einen gegebenen Startwert [math] z [/math] konvergiert.
Da jegliche Anstrengungen Cayleys und anderer Mathematiker keine Resultate zeigten, wurde die Arbeit die darauffolgenden Jahre eingestellt. Erst zu beginn des 20. Jahrhunderts, als von der Französischen Akademie für Naturwissenschaften ein Preis angekündigt wurde, nahmen zahlreiche Mathematiker die Arbeit erneut auf. Die Mathematiker, die erfolgreiche Resultate hervorbrachten, waren Pierre Fatou und Gaston Julia, die mit ihrer entwickelten Theorie der Iterationen rationaler Funktionen in der komplexen Ebene das Problem lösten.
Julia lieferte hierbei eine konkrete Beschreibung von komplexwertigen Mengen, für deren Punkte die Orbits bei Anwendung auf eine rationale Funktion beschränkt bleiben und gewann den ersten Preis. Fatou, der ähnliche Ideen wie Julia in seiner Arbeit vorstellte, erhielt den zweiten Preis. In den nächsten Jahren wuchs das Interesse an diesem Thema sehr stark an und zahlreiche bekannte Mathematiker wie Harald Cramer widmeten ihre Aufmerksamkeit der Julia-Mengen. Doch aufgrund der fehlenden Möglichkeiten Rechenmaschinen für die aufwendigen Berechnung zu benutzen, gerieten auch die Julia-Mengen mit den Jahre in Vergessenheit.
Erst 1977 gelang es dem französische Mathematiker Benoit Mandelbrot mithilfe von Computergrafik die Schönheit der Julia-Mengen visualisieren.
Definition
Sei [math]f[/math] eine auf ganz [math]\mathbb{C}[/math] meromorphe Funktion. Des Weiteren sei [math]\mathrm{grad}(f) \gt 1[/math]. Definiere für ein [math]z \in \hat{\mathbb{C}} := \mathbb{C} \cup \{\infty\}[/math] den dynamischen Prozess \begin{align*} z \mapsto f(z) \end{align*} wodurch ausgehend von einem Startpunkt [math]z_0 \in \hat{\mathbb{C}}[/math] die Rekursion \begin{align*} z_{n+1} = f(z_n), \qquad n \in \mathbb{N}_0. \end{align*} ensteht. Dadurch erhält man die Folge [math]z_0 \mapsto f(z_0) =: f^1(z_0) \mapsto f(f(z_0)) =: f^2(z_0)\mapsto \cdots[/math] von komplexen Zahlen, wobei hier mit [math]f^n, n \in \mathbb{N}[/math] , die n-malige Hintereinanderausführung von [math]f[/math] gemeint ist. Die Folge [math]f^n(z_0)[/math] weist nun zwei grundlegende Verschiedenheiten auf:
- Die Iteration führt unter dem Startwert [math]z_0[/math] zu einer stabiler Dynamik. D.h. [math]|f^t(z_0)|[/math] strebt für steigende [math]n[/math] gegen unendlich. Solche Startwerte werden dann der Fatou-Menge zugeordnet. Die Fatou-Menge zu einer gegebenen Funktion [math]f[/math] wird mit [math]F(f)[/math] abgekürzt.
- Die Iteration führt unter dem Startwert [math]z_0[/math] zu einer instabilen Dynamik. D.h. [math]|f^n(z_0)|[/math] bleibt beschränkt für steigende [math]n[/math]. Solche Startwerte werden dann der Julia-Menge zugeordnet. Die Julia-Menge zu einer gegebenen Funktion [math]f[/math] wird mit [math]J(f)[/math] abgekürzt.
Man sieht sofort, dass [math]J(f) = \mathbb{C}\setminus F(f) = F(f)^c[/math] und somit [math]J(f) \cup F(f) = \mathbb{C}[/math]. Aufgrund dieser Eigenschaft wird sich in diesem Artikel aussließlich auf die Julia-Menge bezogen. Eine Definition der Julia-Menge geschieht über den Abschluss ihrer abstoßenden periodischen Punkte in Abhängigkeit von der gegebenen Funktion [math]f[/math]. Ein Punkt [math]z_0[/math] heißt periodisch falls es ein [math]n \in \mathbb{N}[/math] gibt, sodass [math]z_0 = z_n[/math] gilt. Ein periodischer Punkt [math]z_0[/math] heißt abstoßend, falls [math]|(f^n)'(z_0)| \gt 1[/math] gilt. Formal setzt man also \begin{align*} J(f) = \overline{\left\{z \in \mathbb{C} \big| z\ \text{ist abstoßender periodischer Punkt} \right\}}. \end{align*} Für Polynome mit einem Grad [math]\geq 2[/math] kann die Definition vereinfacht werden zu \begin{align*} J(f) = \partial\left\{z \in \hat{\mathbb{C}} \big| \lim\limits_{t \rightarrow \infty} |f^t(z)|<\infty \right\}. \end{align*}
Grundlegende Eigenschaften
Julia-Mengen können sowohl zusammenhängend als auch nicht zusammenhängend sein.
2. [math] J(f_c)[/math] und [math]J(f_ c¯) [/math] liegen symmetrisch zur imaginären Achse.
Chaotisch:
Sei [math] f[/math] ein Polynom vom Grad ≥ 2 mit der Julia-Menge. Dann ist [math] f[/math] auf der Julia-Menge chaotisch.
Auffällig ist auch, dass es bereits bei kleinen Änderungen von z, zu einem anderen Verhalten kommt.
Julia-Menge eines beliebigen Polynoms:
Die Julia-Menge eines Polynoms [math]f [/math] vom Grad ≥ 2 ist nichtleer und kompakt.
Julia-Mengen von quadratischen Polynomen
Julia-Mengen von quadratischen Polynomen sind besonders interessant.
Man nehme beispielsweise:
[math] f_c: ℂ → ℂ[/math]
[math] z → z^2+c[/math]
Wenn man nun für c=0 einsetzt, kommt man auf folgendes:
[math] f(z)=z^2+c[/math]
Hier gilt:
[math] f(z)=z^2[/math]
K(f) = { z| |z| ≤ 1 } und J(f) = {z ∈ ℂ| |z| = 1 }
Zu erwähnen sei auch, dass [math] f_c[/math] für c = 0 als Julia-Menge den Einheitskreis besitzt.
Setzt man jetzt für c andere Werte ein, verändert sich die Julia-Menge.
| 1 | [math] f(z)=z^2+1[/math] | [math] z_0 = 0 : f_1(z_0) = 1 [/math] |
| [math] f_1 ²(0)=2[/math] | ||
| [math] f_1 ³ (0)= 5[/math] | ||
| -1 | [math] f(z)=z^2-1[/math] | [math] z_0 = 0 : f_{-1}(z_0) = - 1 [/math] |
| [math] f_{-1} ²(0)=2[/math] | ||
| [math] f_{-1} ²(0)=-5[/math] |
Um die Veränderung der Julia- Mengen in Zusammenhang mit anderen c- Werten besser nachzuvollziehen, kann man sich dieses Bild anschauen:
Hier kann man nochmal genau sehen, wie aus dem Einheitskreis bei c=0, bei veränderten c- Werten wie beispielsweise c=-0.4 c=-0.8 und c=-1, andere kreisförmige Körper entstehen.
Symmetrie:
Für die Julia-Menge [math] J(f_c)[/math] von [math]f_{n+1}(z)=z_n^2+c[/math] gilt:
1. [math] J(f_c)[/math] ist punktsymmetrisch zum Ursprung: [math]z \in\ J(f_c) ⇔ -z \in\ J(f_c)[/math]
| Beweis. | [math] f_{n+1}(-z)=(-z)^2+c=f_{n+1}(z) , [/math] |
|---|---|
| [math] (f_{n+1})^k(-z)=(f_{n+1})^{n-1}(f_{n+1}(-z))=(f_{n+1})^{n-1} (f_{n+1}(z))=(f_{n+1})^k(z)[/math] |
2. [math] J(f_c)[/math] und [math]J(f_ \overline {c}) [/math] liegen symmetrisch zur imaginären Achse.
Graphische Darstellung
Zur graphischen Darstellung von Julia-Mengen von einem ausgehenden Startwert [math] z_0 \in \mathbb{C}[/math] wird eine Farbe eines Punktes danach gewählt, wie viele Iterationen notwendig waren, bis [math]|z_n| \geq m \geq 2[/math] ([math]m \in \mathbb{N}[/math] beliebig), da im Allgemeinen die Iterationen für alle [math]z_0[/math] mit [math]|z_0| \geq 2[/math] divergieren. Die Wahl von [math]m= 2[/math] ist grundsätzlich möglich, jedoch werden bei einer größeren Wahl von [math]m[/math] (z.B.[math]m=1000[/math]) qualitativ hochwertigere Bilder ausgegeben . Ist nach einer vorgegebene Iterationszahl [math]n[/math] ein Punkt betragsmäßig kleiner als [math]m[/math] so wird angenommen, dass der Punkt konvergiert. Diese Punkte werden in der Regel dunkel gefärbt, dementsprechend werden Punkte die schneller Konvergieren heller gefärbt. Der nachfolgende Python-Code[2] stellt für einen gegebenen Punkt [math]c[/math] nach [math]n[/math] Iterationen die gewünschte Julia-Menge dar.
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
import os
from matplotlib import cm
from collections import OrderedDict
my_path = os.path.abspath(__file__)
start_time = time.time()
def Julia(f, zmin, zmax, m, n, tmax=256):
x1 = np.linspace(zmin.real, zmax.real, n)
y1 = np.linspace(zmin.imag, zmax.imag, m)
X, Y = np.meshgrid(x1, y1)
Z = X + 1j * Y
J = np.ones(Z.shape) * tmax
for _ in range(tmax):
mask = np.abs(Z) <= 2.
Z[mask] = f(Z[mask])
J[~mask] = J[~mask] - 1.
return J
def f1(z, c=-0.8 + 0.2j):
return z**2 + c
zmin = -1.3 - 1j * 1.3
zmax = 1.3 + 1j * 1.3
J = Julia(f1, zmin, zmax, m=1024, n=1024)
# save array J as a PNG color image
name = "testjulia2.png"
cmap = cm.get_cmap("nipy_spectral")
plt.imsave(my_path + name, J, cmap=cmap, origin="lower")
Hierbei wird als Funktionen [math]f[/math] ein Polynom zweiten Grades gewählt, also [math]f=z^2+c[/math]. Das Paket numpy wird verwendet um die nötigen Berechnungen effizient in vektorisierter Form zu lösen anstatt diese aufwendig mithilfe von Schleifen zu berechnen.
Mandelbrot-Menge
Definition über die Julia-Mengen
Die Mandelbrotmenge wurde zur Klassifizierung der Julia-Mengen definiert. Sie umfasst die Teilmenge der komplexen Zahlen, für welche die Julia Menge zusammenhängend ist. Die Mandelbrotmenge lässt sich rekursiv, wie folgt definieren:
- [math] M=\{c\in \mathbb{C}\mid z_{n+1}=z_n^2+c \text{ bleibt beschränkt } \forall n\in \mathbb{N} [/math] mit [math]z_0 = 0 [/math]
Um nun für bestimmte Werte [math]c\in\mathbb{C}[/math] zu bestimmen, ob sie in der Mandelbrotmenge enthalten sind, führt man [math]n\in\mathbb{N}[/math] Iterationen durch. Wenn gilt [math]\mid f^n_c(0)\mid \gt 2[/math], so färbt man den entsprechenden Punkt weiß, er liegt also nicht in [math]M[/math]. Ansonsten färbt man ihn schwarz. Desto größer [math]n[/math] gewählt wird, desto genauer wird das Bild, dass man erhält. In der Mathematik sind theoretisch beliebige Genauigkeiten möglich, dies führt zu den faszinierenden graphischen Darstellungen der Mandelbrotmenge, wenn man weiter reinzoomt.
Abhängig von der Definition der Juliamenge lässt sich die Mandelbrotmenge, wie folgt definieren:
- [math]M=\{c\in \mathbb{C}\mid J(f) \text{ ist zusammenhängend}\}[/math]
Weitere Definitionen der Mengen sind:
- [math] M=\{c\in\mathbb{C}\mid f^n_c(0)\not\to\infty\text{, wenn } n\to \infty\}=\{c\in\mathbb{C}\mid (z_n)_{n\in\mathbb{N}} \text{ ist beschränkt}\}[/math]
Diese Darstellungen lassen sich mithilfe der oberen Definition beweisen.[3]
Grundlegende Eigenschaften
Grenzverhalten ausgewählter Funktionen
Für verschiedene Punkte [math]c\in\mathbb{C}[/math] lassen sich vier verschiedene Grenzverhalten beobachten:
- Konvergenz gegen einen Punkt
- Die Glieder bilden einen Zyklus mit zwei oder mehr Werten
- chaotisches aber beschränktes Verhalten der Glieder
- Divergenz gegen unendlich
Ein Punkt [math]c\in\mathbb{C}[/math] ist in [math]M[/math] falls er eines der ersten drei Grenzverhalten aufzeigt.
| Parameter (c) | Folgeglieder (z_2, z_3, z_4,...) | Grenzverhalten | Ist c in M? |
|---|---|---|---|
| 1 | 2, 5, 26,... | bestimmte Divergenz gegen [math]\infty[/math] | [math]1\notin M[/math] |
| 0 | 0, 0, 0,... | Konvergenz gegen 0 | [math]0\in M[/math] |
| -1 | 0, -1, 0,... | Zweierzyklus | [math]-1\in M[/math] |
| i | -1+i, -i, -1+i,... | Zweierzyklus | [math]i\in M[/math] |
| -1,5 | 0,75, [math] -\frac{15}{16}[/math], [math] -\frac{159}{256}[/math],... | Chaos (beschränkt) | [math]-1,5\in M[/math] |
| -2 | 2, 2, 2,... | Konvergenz gegen 2 | [math]2\in M[/math] |
| 0,25 | [math] \frac{5}{16}[/math], [math] \frac{89}{256}[/math], [math] \frac{24305}{65536}[/math],... | Konvergenz gegen 0,5 | [math]0,25\in M[/math] |
M ist kompakt
Die Mandelbrotmenge ist abgeschlossen, da ihr Komplement offen ist. Außerdem liegt sie innerhalb eines Kreises um den Ursprung mit Radius 2, daraus folgt Beschränktheit.
[math]M\subset B_2(0)\subset \mathbb{C}[/math]
Nach dem Satz von Heine-Borel folgt somit Kompaktheit.
M ist spiegelsymmetrisch zur reellen Achse
Diese Tatsache lässt sich leicht anhand der Bilder erkennen. Doch auch bei Betrachtung der mathematischen Grundlagen kann dieser Umstand leicht gezeigt werden. Wir wollen also zeigen, dass wenn [math]a+bi=c\in M[/math] ist, auch [math]a-bi=\overline c \in M[/math] ist.
| [math]n[/math] | [math]z_{n+1}=z_{n}+c[/math] | [math]z_{n+1}=z_{n}+\overline c[/math] |
|---|---|---|
| 1 | [math]0+a+bi[/math] | [math]0+a-bi[/math] |
| 2 | [math](a+bi)^2+a+bi=(a^2-b^2+a)+i(b+2ab)[/math] | [math](a-bi)^2+a-bi=(a^2-b^2+a)-i(b+2ab)[/math] |
| 3 | [math]((a^2-b^2+a)+i(b+2ab))^2 + a + bi \\= (a^2-b^2+a)^2-(b+2ab)^2+a+i(2((a^2-b^2+a)(b+2ab)+b)) [/math] | [math]((a^2-b^2+a)-i(b+2ab))^2 + a - bi \\= (a^2-b^2+a)^2-(b+2ab)^2+a-i(2((a^2-b^2+a)(b+2ab)+b)) [/math] |
| n | [math] Re(z_n)+i*Im(z_n)[/math] | [math] Re(z_n)-i*Im(z_n)[/math] |
Wir sehen hier, dass für [math]z_{n+1}=z_n+c[/math] und [math]\overline{z_{n+1}}=z_n+\overline c[/math] gilt: [math]Re(z_n)=Re(\overline z_n) [/math] und [math]Im(z_n)=Im(\overline z_n) [/math] . Die Beträge sind also identisch und Realteil und Imaginärteil entsprechen einander. Daraus lässt sich folgern, wenn ein Werte nicht gegen unendlich divergiert, so auch nicht sein komplex konjugierter Wert. Somit ergibt sich:
[math]a+bi=c_1\in M\rightarrow a-bi=\overline c_1 \in M[/math]
Also entsteht ein achsensymmetrisches Bild.
M ist zusammenhängend
Diese Tatsache wurde 1984 von Adrien Douady und John Hamal Hubbard bewiesen. Ob sie auch lokal zusammenhängend ist, ist noch eine offene Frage.
Graphische Darstellung
Es gibt verschiedene farbliche Visualisierungen der Mandelbrotmenge, aber nach Konvention sind alle Punkte, die zur Mandelbrotmenge dazugehören, schwarz eingezeichnet, d.h. alle [math]c[/math], für die die Folge [math]z_{n}[/math] beschränkt bleibt. Die sich so ergebende Menge wird auch als »Apfelmännchen« bezeichnet, was sich einem erschließt, wenn man den Kopf um 90 Grad nach links neigt. Bei näherer Betrachtung der Mandelbrotmenge erkennt man, dass sich die Struktur des Apfelmännchens am Rand der Menge in kleinerer Ausführung wiederholt.
Alles, was nicht schwarz eingefärbt ist, gehört nicht zur Mandelbrotmenge. Die verschiedenen Farbbereiche um die Mandelbrotmenge herum geben an, wie schnell die Folge für ein [math]c[/math] in dem jeweiligen Bereich divergiert.
Auf Geogebra hat man die Möglichkeit, sich das Konvergenz- bzw. Divergenzverhalten der Folge [math]z_{n}[/math] für verschiedene [math]c[/math] darstellen zu lassen. Zudem werden durch Schraffieren auf der komplexen Ebene alle zur Mandelbrotmenge zugehörigen Punkte sichtbar. Allerdings treten bei dem Programm Rundungsfehler auf, z.B. scheint bei Geogebra die Folge für [math]c=i[/math] zu divergieren, obwohl man berechnen kann, dass sie für [math]i[/math] beschränkt bleibt.
Geschichte
Fraktale waren schon lange vor dem französischen Mathematiker Benoît B. Mandelbrot (1924-2010) ein untersuchtes Teilgebiet der Mathematik. So veröffentlichte der schwedische Mathematiker Helge von Koch (1870-1924) seine berühmte Koch-Kurve (auch »Schneeflockenkurve«) bereits 1904 – noch früher, im Jahr 1890, stellte der italienische Mathematiker Guiseppe Peano (1858-1932) die Peano-Kurve vor. Beides sind Beispiele für Fraktale, aber erst 1975 gab Mandelbrot solchen Gebilden schließlich einen Namen (abgeleitet aus dem Lateinischen »fractus« = gebrochen), weshalb er auch »Vater der Fraktale« genannt wird.
1967 befasste er sich mit der Frage, wie man die Länge von Großbritanniens Küste, ebenfalls einem Fraktal, messen könne. Dabei stieß Mandelbrot auf das Problem, unterschiedliche Ergebnisse zu bekommen, je nachdem wie genau er vorging und wie stark er manche feinere Ausbuchtungen bei der Messung vereinfacht nur als glatte Kurve einberechnete.
1980 veröffentlichte er schließlich seine Arbeit über die Mandelbrotmenge, deren Ursprung in den Julia-Mengen liegt, die schon 1905 von Gaston Maurice Julia und Pierre Fatou untersucht wurden. Schon zwei Jahre vor dieser Veröffentlichung gab es erste graphische Darstellungen der Mandelbrotmenge am Computer.
Weblinks
https://www.youtube.com/watch?v=lO1B2uA4l38 -Eine Dokumentation über Fraktale, die unter anderem auch den kommerziellen Erfolg der Mandelbrot-Menge zeigt
Einzelnachweise
Autoren
- Mansur Daschaew
- Hannah Otte
- Selin Koparan
- Danielle Eitelmann