Fibonacci Folge: Unterschied zwischen den Versionen
K |
|||
| (17 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Die Fibonacci | + | Die Fibonacci Folge ist eine Folge natürlicher Zahlen. Konstruiert wird sie durch folgende, rekursive Bildungsvorschrift: |
| + | |||
| + | <math> f_{n}=f_{n-1}+f_{n-2} </math> | ||
| + | |||
| + | mit den Startwerten <math> f_1=f_2=1 </math>. | ||
<math> | <math> | ||
| Zeile 6: | Zeile 10: | ||
1 & 1 & 2 & 3 & 5 & 8 & 13 & 21 & 34 & 55 | 1 & 1 & 2 & 3 & 5 & 8 & 13 & 21 & 34 & 55 | ||
\end{array} \cdots </math> | \end{array} \cdots </math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Verhältnis zweier aufeinanderfolgender Fibonacci-Zahlen== | ==Verhältnis zweier aufeinanderfolgender Fibonacci-Zahlen== | ||
| Zeile 23: | Zeile 21: | ||
| style="text-align:left; font-size: 95%;" | '''Beweis''' | | style="text-align:left; font-size: 95%;" | '''Beweis''' | ||
|- | |- | ||
| − | | | + | |Diese Behauptung lässt sich leicht mit der weiter unten bewiesenen Formel von Moivre und Binet beweisen: |
| − | |||
| − | Diese Behauptung lässt sich leicht mit der weiter unten bewiesenen Formel von Moivre und Binet beweisen: | ||
<math> | <math> | ||
\begin{array}{rcl} | \begin{array}{rcl} | ||
| − | \frac{f_{n+1}}{f_n}&=&\frac{\frac{\Phi^{n+1}-(1-\Phi)^{n+1}}{\sqrt{5}}}{\frac{\Phi^n-(1-\Phi)^n}{\sqrt{5}}} | + | \frac{f_{n+1}}{f_n}&=&\frac{\frac{\Phi^{n+1}-(1-\Phi)^{n+1}}{\sqrt{5}}}{\frac{\Phi^n-(1-\Phi)^n}{\sqrt{5}}} =\frac{\Phi^{n+1}-(1-\Phi)^{n+1}}{\Phi^n-(1-\Phi)^n} |
| − | + | & | |
\end{array} | \end{array} | ||
</math> | </math> | ||
| Zeile 46: | Zeile 42: | ||
== Kaninchen-Aufgabe == | == Kaninchen-Aufgabe == | ||
| − | Eine Anwendungsbeispiel findet die Fibonacci Folge bei der Kaninchenpopulation. | + | Eine Anwendungsbeispiel findet die [https://funfacts.mathi.uni-heidelberg.de/index.php/Fibonacci_Folge Fibonacci Folge] bei der Kaninchenpopulation. |
| − | Es startet ein männliches | + | Es startet ein männliches und ein weibliches Kaninchenneugeborenes (ein Paar). Angenommen ein Neugeborenes braucht ein Monat um auszuwachsen, ein Paar bekommt pro Monat ein Paar Neugeborenes und kein Kaninchen stirbt. |
| − | Im ersten Monat sind es also ein Paar Neugebore, im 2. Monat sind sie Erwachsen, also keine Neugeborenen. Dann bekommen sie ein Paar Neugeborene. | + | Im ersten Monat sind es also ein Paar Neugebore, im 2. Monat sind sie Erwachsen, also keine Neugeborenen. Dann bekommen sie ein Paar Neugeborene im dritten Monat und so weiter. |
| − | Es gibt also im ersten Monat keine Erwachsenen, im zweiten Monat dann ein Paar Erwachsene, 3. Monat 1 Paar, | + | Es gibt also im ersten Monat keine Erwachsenen, im zweiten Monat dann ein Paar Erwachsene, 3. Monat 1 Paar, im vierten Monat 2 Paare und so weiter. |
Wenn man sich nun also die Gesamtpopulation anguckt folgt: | Wenn man sich nun also die Gesamtpopulation anguckt folgt: | ||
| Zeile 78: | Zeile 74: | ||
\end{align*} </math> | \end{align*} </math> | ||
| − | Hier in dem vereinfachten Beispiel beschreibt also die | + | Hier in dem vereinfachten Beispiel beschreibt also die [https://funfacts.mathi.uni-heidelberg.de/index.php/Fibonacci_Folge Fibonacci Folge] die Gesamtpopulation der Kaninchen, sowie die jeweiligen Populationen der erwachsenen Kaninchen ab dem zweiten Monat, bzw. auch die neugeborenen Population der Kaninchen ab dem dritten Monat. |
<ref>Koshy, Thomas: Fibonacci and Lucas numbers with applications: Chapter 2 </ref> | <ref>Koshy, Thomas: Fibonacci and Lucas numbers with applications: Chapter 2 </ref> | ||
== Matrixdarstellung == | == Matrixdarstellung == | ||
| − | Man kann | + | Man kann die Fibonacci Folge auf verschiedene Weisen darstellen. Hier ein Beispiel für die Darstellung in einer Matrix: |
<math>\begin{align*} | <math>\begin{align*} | ||
| − | |||
\left( | \left( | ||
\begin{array}{cc} | \begin{array}{cc} | ||
| − | + | f_{n+1}& f_n \\ | |
| − | + | f_n & f_{n-1} | |
| − | 1 | ||
\end{array} | \end{array} | ||
| − | + | \right) | |
| − | \right) | + | = |
\left( | \left( | ||
| Zeile 102: | Zeile 96: | ||
\begin{array}{cc} | \begin{array}{cc} | ||
| − | + | 1&1 \\ | |
| + | |||
| + | 1&0 | ||
| − | |||
\end{array} | \end{array} | ||
| − | + | \right)^n | |
| − | \right) | ||
| − | |||
\end{align*}</math> | \end{align*}</math> | ||
| − | Die n-te potenz der Matrix <math>A = \left( \begin{array}{cc} 1&1 \\1&0 \end{array} \right)</math> gibt die n-te Fibonaccizahl auf der Gegendiagonalen an. | + | Die n-te potenz der Matrix <math>A = \left( \begin{array}{cc} 1&1 \\1&0 \end{array} \right)</math> gibt die n-te Fibonaccizahl auf der Gegendiagonalen an, aufgrund der Matrixmultiplikation. |
== Pisano-Folge == | == Pisano-Folge == | ||
| − | Betrachten wir nun | + | Betrachten wir nun eine Folge modulo einer Primzahl <math>p \in \mathbb{P} </math>, d.h. über dem Restklassenkörper <math> \mathbb{Z}/_{p\mathbb{Z}} </math> |
| − | + | Nun gucken wir uns die Fibonaccifolge: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | Nun gucken wir uns die Fibonaccifolge | ||
| − | |||
0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368,121393,196418,317811,514229,832040,1346269 | 0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368,121393,196418,317811,514229,832040,1346269 | ||
| − | + | über dem Restklassenkörper <math> \mathbb{Z}/_{7\mathbb{Z}} </math> an. Wir erhalten: | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
0,1,1,2,3,5,1,6,0,6,6,5,4,2,6,1,0,1,1,2,3,5,1,6,0,6,6,5,4,2,6,1,0 | 0,1,1,2,3,5,1,6,0,6,6,5,4,2,6,1,0,1,1,2,3,5,1,6,0,6,6,5,4,2,6,1,0 | ||
| − | + | Wir sehen, dass die Folge sich nach 16 Werten wiederholt. Außerdem ist die Restklassenfolge wieder eine Fibonaccifolge, da <math>f_n=f_{n-1}+f_{n-2}</math> man braucht also nicht die Restklasse von jeder einzelnen Werte der Fibonaccifolge in <math>\mathbb{Z}</math> bilden, sondern kann die Folge direkt in der Restklasse bilden | |
| − | Auf <math>\mathbb{Z/2\mathbb{Z}}</math> wiederholt sich die Folge nach 3 Schritten: 0,1,1.... | + | Auf <math>\mathbb{Z}/_{2\mathbb{Z}}</math> wiederholt sich die Folge nach 3 Schritten: 0,1,1.... |
| − | <math>\mathbb{Z/3\mathbb{Z}}</math> nach 8 Schritten: 0,1,1,2,0,2,2,1,0.... | + | <math>\mathbb{Z}/_{3\mathbb{Z}}</math> nach 8 Schritten: 0,1,1,2,0,2,2,1,0.... |
==Erweiterung== | ==Erweiterung== | ||
| Zeile 158: | Zeile 139: | ||
Dementsprechend nähert sich das Verhältnis zweier aufeinanderfolgender Fibonacci-Zahlen im Negativen gegen <math> -\frac{1}{\Phi} </math> an. | Dementsprechend nähert sich das Verhältnis zweier aufeinanderfolgender Fibonacci-Zahlen im Negativen gegen <math> -\frac{1}{\Phi} </math> an. | ||
| − | Bei der Fibonacci-Folge sind die ersten beiden Glieder 1. Also <math>f_1 = f_2 = 1</math>. Damit ist die Fibonaccifolge vollständig definiert. | + | Bei der Fibonacci-Folge sind die ersten beiden Glieder 1. Also <math>f_1 = f_2 = 1</math>. Damit ist die Fibonaccifolge vollständig definiert. Eine andere Folge erhält man, wenn man <math>f_1 = 2</math> und <math>f_2 = 1</math> nimmt. Diese Folge wird auch Lucas-Folge genannt: |
<math> | <math> | ||
| Zeile 185: | Zeile 166: | ||
</math> | </math> | ||
| − | <math>\Phi</math> ist dabei der [[ | + | <math>\Phi</math> ist dabei der [[Goldener Schnitt]] <math>\Phi=\frac{1+\sqrt{5}}{2}</math>. Diese Formel liefert für ganzzahlige Werte für n auch exakte, ganzzahlige Ergebnisse. |
{| class="wikitable left mw-collapsible mw-collapsed font-size: 105.3%;" | {| class="wikitable left mw-collapsible mw-collapsed font-size: 105.3%;" | ||
| style="text-align:left; font-size: 95%;" | '''Beweis durch vollständige Induktion''' | | style="text-align:left; font-size: 95%;" | '''Beweis durch vollständige Induktion''' | ||
|- | |- | ||
| − | | | + | | |
| − | |||
Um zu zeigen, dass diese Formel die Fibonacci-Zahlen ergibt, überprüfen wir die Bildungsvorschrift: | Um zu zeigen, dass diese Formel die Fibonacci-Zahlen ergibt, überprüfen wir die Bildungsvorschrift: | ||
| − | '''IA''': Die Formel gilt für <math>n=0\ \left(\frac{\Phi^0-(1-\Phi)^0}{\sqrt{5}}=\frac{1-1}{\sqrt{5}}=0=f_0\right)</math> und für <math> n=1\ \left( | + | '''IA''': Die Formel gilt für <math>n=0\ \left(\frac{\Phi^0-(1-\Phi)^0}{\sqrt{5}}=\frac{1-1}{\sqrt{5}}=0=f_0\right)</math> und für <math> n=1\ \left( \frac{\Phi^1-(1-\Phi)^1}{\sqrt{5}}=\frac{\sqrt{5}}{\sqrt{5}}=1=f_1\right)</math>. |
'''IV''': Nun gelte sie für ein <math> n,\ n-1\in\mathbb{N}</math>. | '''IV''': Nun gelte sie für ein <math> n,\ n-1\in\mathbb{N}</math>. | ||
| Zeile 222: | Zeile 202: | ||
===Erweiterung auf eine kontinuierliche Funktion=== | ===Erweiterung auf eine kontinuierliche Funktion=== | ||
| − | Nun stellt sich die Frage | + | Nun stellt sich die Frage was passiert, wenn wir in die Formel von Moivre-Binet nicht-ganzzahlige Werte für n einsetzen, die Fibonacci-Folge also in eine kontinuierliche Funktion umwandeln. Da <math>1-\Phi</math> jedoch negativ ist, und nicht-ganzzahlige Potenzen von negativen Zahlen nur im Komplexen definiert sind, müssen wir den Wertebereich auf <math>\mathbb{C}</math> erweitern: |
<math> | <math> | ||
| Zeile 232: | Zeile 212: | ||
Der Graph dieser Funktion sieht wie folgt aus (Darstellung als Kurve mit Kurvenparameter x): | Der Graph dieser Funktion sieht wie folgt aus (Darstellung als Kurve mit Kurvenparameter x): | ||
<gallery> | <gallery> | ||
| − | Datei: | + | Datei:Binet2.PNG|<math> -5\leq x\leq0</math> |
| − | Datei:Binet1 (1). | + | Datei:Binet1 (1).PNG|<math> 0\leq x\leq5</math> |
</gallery> | </gallery> | ||
Eine andere Darstellung sieht wie Folgt aus: | Eine andere Darstellung sieht wie Folgt aus: | ||
<gallery> | <gallery> | ||
| + | Datei:Im Binet.PNG|Imaginärteil der Moivre-Binet-Funktion | ||
Datei:Re Binet.PNG|Realteil der Moivre-Binet-Funktion | Datei:Re Binet.PNG|Realteil der Moivre-Binet-Funktion | ||
| − | |||
</gallery> | </gallery> | ||
==Kompexe Fibonacci-Funktion== | ==Kompexe Fibonacci-Funktion== | ||
| − | Wir haben bereits gesehen, dass wir die Fibonaccifolge | + | Wir haben bereits gesehen, dass wir die Fibonaccifolge zu einer komplexwertige Funktion mit reellen Eingabewerten erweitern können. Nun können wir dieses Konzept noch weiter abstrahieren, indem wir auch komplexe Eingabewerte zulassen: |
<math> | <math> | ||
\begin{array}{rl} | \begin{array}{rl} | ||
| − | f:&\mathbb{C}\to\mathbb{C}\\& | + | f:&\mathbb{C}\to\mathbb{C}\\&z\mapsto f(z)=\frac{\Phi^z-(1-\Phi)^z}{\sqrt{5}} |
\end{array} | \end{array} | ||
</math> | </math> | ||
| − | + | Da die Darstellung komplexer Funktionen immer etwas kompliziert ist, zeigen wir mehrere Darstellungsmöglichkeiten: | |
<gallery> | <gallery> | ||
| − | Datei:Cmplx binet colour.PNG|Darstellung mittels Domain colouring | + | Datei:Cmplx binet colour.PNG|alt=Beim Domain colouring steht die Farbe für das Argument des Funktionswertes an dieser Stelle und die Intensität (meißt relativ schwer erkennbar) für den Betrag.|Darstellung mittels [[wikipedia:Domain_coloring|Domain colouring]] |
</gallery> | </gallery> | ||
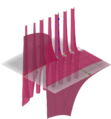
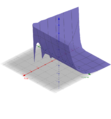
| − | + | Bei einer anderen Art der Darstellung stellt man den Real- und Imaginärteil der Funktionswerte als Funktionen <math> | |
| + | \mathbb{R}^2\to\mathbb{R} | ||
| + | </math> dar. Im Folgenden ist dies mit dem Funktionen-Plotter Geogebra dargestellt (Bemerkung: Da Geogebra keine sonderlich exakte Berechnung ermöglicht, sind diese Bilder etwas ungenauer): | ||
<gallery> | <gallery> | ||
Datei:Realteil_der_komplexen_Moivre-Binet-Formel.png|Realteil | Datei:Realteil_der_komplexen_Moivre-Binet-Formel.png|Realteil | ||
| Zeile 269: | Zeile 251: | ||
===Nullstellen=== | ===Nullstellen=== | ||
| − | Wie man bereits anhand der Bilder (mehr oder weniger gut) erkennen kann, liegen alle Nullstellen auf einer Gerade durch den Nullpunkt. Genauer lassen sich alle Nullstellen <math> | + | Wie man bereits anhand der Bilder (mehr oder weniger gut) erkennen kann, liegen alle Nullstellen auf einer Gerade durch den Nullpunkt. Genauer lassen sich alle Nullstellen <math>z_n</math> darstellen als: |
| − | <math> | + | <math>z_n=n\cdot\frac{2\pi i}{\ln(\Phi)-\ln(1-\Phi)}\qquad n\in\mathbb{Z}</math> |
{| class="wikitable left mw-collapsible mw-collapsed font-size: 105.3%;" | {| class="wikitable left mw-collapsible mw-collapsed font-size: 105.3%;" | ||
| style="text-align:left; font-size: 95%;" | '''Beweis''' | | style="text-align:left; font-size: 95%;" | '''Beweis''' | ||
|- | |- | ||
| − | | | + | | |
| − | |||
Es gilt: | Es gilt: | ||
| Zeile 291: | Zeile 272: | ||
|} | |} | ||
<references /> | <references /> | ||
| + | |||
| + | == Autoren == | ||
| + | Ines Christa, Konrad Kockler, Sebastian Splitthoff, Dennis Straub | ||
Aktuelle Version vom 12. April 2021, 13:35 Uhr
Die Fibonacci Folge ist eine Folge natürlicher Zahlen. Konstruiert wird sie durch folgende, rekursive Bildungsvorschrift:
[math] f_{n}=f_{n-1}+f_{n-2} [/math]
mit den Startwerten [math] f_1=f_2=1 [/math].
[math] \begin{array}{c|c|c|c|c|c|c|c|c|c} f_{1} & f_{2} & f_{3} & f_{4} & f_{5} & f_{6} & f_{7} & f_8 & f_9 & f_{10}\\\hline 1 & 1 & 2 & 3 & 5 & 8 & 13 & 21 & 34 & 55 \end{array} \cdots [/math]
Verhältnis zweier aufeinanderfolgender Fibonacci-Zahlen
Die Folge [math] \left(\frac{f_{n+1}}{f_n}\right)_{n\in\mathbb{N}} [/math] der Verhältnisse zweier aufeinanderfolgender Fibonacci-Zahlen konvergiert in [math]\mathbb{R}[/math] mit folgendem Grenzwert:
[math]\lim_{n\to\infty}\frac{f_{n+1}}{f_n}=\frac{1+\sqrt{5}}{2}:=\Phi[/math]
[math]\Phi[/math] wird auch Goldener Schnitt genannt.
| AusklappenBeweis |
Kaninchen-Aufgabe
Eine Anwendungsbeispiel findet die Fibonacci Folge bei der Kaninchenpopulation.
Es startet ein männliches und ein weibliches Kaninchenneugeborenes (ein Paar). Angenommen ein Neugeborenes braucht ein Monat um auszuwachsen, ein Paar bekommt pro Monat ein Paar Neugeborenes und kein Kaninchen stirbt.
Im ersten Monat sind es also ein Paar Neugebore, im 2. Monat sind sie Erwachsen, also keine Neugeborenen. Dann bekommen sie ein Paar Neugeborene im dritten Monat und so weiter.
Es gibt also im ersten Monat keine Erwachsenen, im zweiten Monat dann ein Paar Erwachsene, 3. Monat 1 Paar, im vierten Monat 2 Paare und so weiter.
Wenn man sich nun also die Gesamtpopulation anguckt folgt:
[math] \begin{align*} \begin{array}[h]{l|c|c|c|c|c|c} Monat & 1 & 2 & 3 & 4 & 5 & 6\\ \hline Erwachsene & 0 & 1 & 1 & 2 & 3 & 5 \\ \hline Neugeborene & 1 & 0 & 1 & 1 & 2 & 3 \\ \hline Gesamt & 1 & 1 & 2 & 3 & 5 & 8\\ \end{array} \end{align*} [/math]
Hier in dem vereinfachten Beispiel beschreibt also die Fibonacci Folge die Gesamtpopulation der Kaninchen, sowie die jeweiligen Populationen der erwachsenen Kaninchen ab dem zweiten Monat, bzw. auch die neugeborenen Population der Kaninchen ab dem dritten Monat. [1]
Matrixdarstellung
Man kann die Fibonacci Folge auf verschiedene Weisen darstellen. Hier ein Beispiel für die Darstellung in einer Matrix:
[math]\begin{align*} \left( \begin{array}{cc} f_{n+1}& f_n \\ f_n & f_{n-1} \end{array} \right) = \left( \begin{array}{cc} 1&1 \\ 1&0 \end{array} \right)^n \end{align*}[/math]
Die n-te potenz der Matrix [math]A = \left( \begin{array}{cc} 1&1 \\1&0 \end{array} \right)[/math] gibt die n-te Fibonaccizahl auf der Gegendiagonalen an, aufgrund der Matrixmultiplikation.
Pisano-Folge
Betrachten wir nun eine Folge modulo einer Primzahl [math]p \in \mathbb{P} [/math], d.h. über dem Restklassenkörper [math] \mathbb{Z}/_{p\mathbb{Z}} [/math] Nun gucken wir uns die Fibonaccifolge: 0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610,987,1597,2584,4181,6765,10946,17711,28657,46368,121393,196418,317811,514229,832040,1346269 über dem Restklassenkörper [math] \mathbb{Z}/_{7\mathbb{Z}} [/math] an. Wir erhalten: 0,1,1,2,3,5,1,6,0,6,6,5,4,2,6,1,0,1,1,2,3,5,1,6,0,6,6,5,4,2,6,1,0
Wir sehen, dass die Folge sich nach 16 Werten wiederholt. Außerdem ist die Restklassenfolge wieder eine Fibonaccifolge, da [math]f_n=f_{n-1}+f_{n-2}[/math] man braucht also nicht die Restklasse von jeder einzelnen Werte der Fibonaccifolge in [math]\mathbb{Z}[/math] bilden, sondern kann die Folge direkt in der Restklasse bilden
Auf [math]\mathbb{Z}/_{2\mathbb{Z}}[/math] wiederholt sich die Folge nach 3 Schritten: 0,1,1....
[math]\mathbb{Z}/_{3\mathbb{Z}}[/math] nach 8 Schritten: 0,1,1,2,0,2,2,1,0....
Erweiterung
Die Bildungsvorschrift lässt sich einfach umstellen:
[math] f_{n}=f_{n+2}-f_{n+1} [/math]
Damit erhält man eine erweiterte Fibonacci-Folge:
[math] \cdots\begin{array}{c|c|c|c|c|c|c|c|c|c|c|c|c|c|c} f_{-7} & f_{-6} & f_{-5} & f_{-4} & f_{-3} & f_{-2} & f_{-1} & f_0 & f_1 & f_2 & f_3 & f_4 & f_5 & f_6 & f_7\\\hline 13 & -8 & 5 & -3 & 2 & -1 & 1 & 0 & 1 & 1 & 2 & 3 & 5 & 8 & 13 \end{array} \cdots [/math]
Die Beträge der Werte sind symmetrisch, im Negtiaven alternieren sie jedoch:
[math] f_{-n}=(-1)^{n+1}f_n[/math]
Dementsprechend nähert sich das Verhältnis zweier aufeinanderfolgender Fibonacci-Zahlen im Negativen gegen [math] -\frac{1}{\Phi} [/math] an.
Bei der Fibonacci-Folge sind die ersten beiden Glieder 1. Also [math]f_1 = f_2 = 1[/math]. Damit ist die Fibonaccifolge vollständig definiert. Eine andere Folge erhält man, wenn man [math]f_1 = 2[/math] und [math]f_2 = 1[/math] nimmt. Diese Folge wird auch Lucas-Folge genannt:
[math] \cdots\begin{array}{c|c|c|c|c|c|c|c|c|c|c|c|c|c|c} f_{-7} & f_{-6} & f_{-5} & f_{-4} & f_{-3} & f_{-2} & f_{-1} & f_0 & f_1 & f_2 & f_3 & f_4 & f_5 & f_6 & f_7\\\hline 47 & -29 & 18 & -11 & 7 & -4 & 3 & -1 & 2 & 1 & 3 & 4 & 7 & 11 & 18 \end{array} \cdots [/math]
Diese Folge ist nicht mehr betragsmäßig symmetrisch zu [math]f_0[/math] sondern zu [math]f_1[/math]:
[math] f_{-n-1}=(-1)^{n}f_{n-1} [/math]
Das Verhältnis zweier aufeinanderfolgender Lucas-Zahlen nähert sich im Unendlichen ebenfalls gegen [math]\Phi[/math] (bzw. [math]-\frac{1}{\Phi}[/math] im Negativen) an.
Kontinuierliche Fibonacci-Funktion
Formel von Moivre-Binet
Die Formel von Moivre und Binet ist eine Formel zur expliziten Berechung der n-ten Fibonacci-Zahl:
[math] \begin{array}{rcl} f:\mathbb{N}&\to&\mathbb{N}\\ n&\mapsto&f_n=\frac{\Phi^n-(1-\Phi)^n}{\sqrt{5}} \end{array} [/math]
[math]\Phi[/math] ist dabei der Goldener Schnitt [math]\Phi=\frac{1+\sqrt{5}}{2}[/math]. Diese Formel liefert für ganzzahlige Werte für n auch exakte, ganzzahlige Ergebnisse.
| AusklappenBeweis durch vollständige Induktion |
Erweiterung auf eine kontinuierliche Funktion
Nun stellt sich die Frage was passiert, wenn wir in die Formel von Moivre-Binet nicht-ganzzahlige Werte für n einsetzen, die Fibonacci-Folge also in eine kontinuierliche Funktion umwandeln. Da [math]1-\Phi[/math] jedoch negativ ist, und nicht-ganzzahlige Potenzen von negativen Zahlen nur im Komplexen definiert sind, müssen wir den Wertebereich auf [math]\mathbb{C}[/math] erweitern:
[math] \begin{array}{rl} f:&\mathbb{R}\to\mathbb{C}\\&x\mapsto f(x)=\frac{\Phi^x-(1-\Phi)^x}{\sqrt{5}} \end{array} [/math]
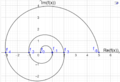
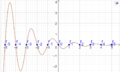
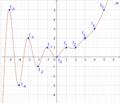
Der Graph dieser Funktion sieht wie folgt aus (Darstellung als Kurve mit Kurvenparameter x):
Eine andere Darstellung sieht wie Folgt aus:
Kompexe Fibonacci-Funktion
Wir haben bereits gesehen, dass wir die Fibonaccifolge zu einer komplexwertige Funktion mit reellen Eingabewerten erweitern können. Nun können wir dieses Konzept noch weiter abstrahieren, indem wir auch komplexe Eingabewerte zulassen:
[math] \begin{array}{rl} f:&\mathbb{C}\to\mathbb{C}\\&z\mapsto f(z)=\frac{\Phi^z-(1-\Phi)^z}{\sqrt{5}} \end{array} [/math]
Da die Darstellung komplexer Funktionen immer etwas kompliziert ist, zeigen wir mehrere Darstellungsmöglichkeiten:
Darstellung mittels Domain colouring
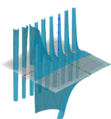
Bei einer anderen Art der Darstellung stellt man den Real- und Imaginärteil der Funktionswerte als Funktionen [math] \mathbb{R}^2\to\mathbb{R} [/math] dar. Im Folgenden ist dies mit dem Funktionen-Plotter Geogebra dargestellt (Bemerkung: Da Geogebra keine sonderlich exakte Berechnung ermöglicht, sind diese Bilder etwas ungenauer):
Interaktive Darstellung mittels Geogebra:
https://www.geogebra.org/m/qhrggvtr
Nullstellen
Wie man bereits anhand der Bilder (mehr oder weniger gut) erkennen kann, liegen alle Nullstellen auf einer Gerade durch den Nullpunkt. Genauer lassen sich alle Nullstellen [math]z_n[/math] darstellen als:
[math]z_n=n\cdot\frac{2\pi i}{\ln(\Phi)-\ln(1-\Phi)}\qquad n\in\mathbb{Z}[/math]
| AusklappenBeweis |
- ↑ Koshy, Thomas: Fibonacci and Lucas numbers with applications: Chapter 2
Autoren
Ines Christa, Konrad Kockler, Sebastian Splitthoff, Dennis Straub