Pi und das Buffon'sche Nadelproblem: Unterschied zwischen den Versionen
K |
|||
| (Eine dazwischenliegende Version desselben Benutzers wird nicht angezeigt) | |||
| Zeile 133: | Zeile 133: | ||
Wir stellen uns vor, die Nadel lässt sich durch einen Anfangspunkt sowie einen Winkel φ beschreiben, da ihre Länge [math]l[\math] konstant ist. | Wir stellen uns vor, die Nadel lässt sich durch einen Anfangspunkt sowie einen Winkel φ beschreiben, da ihre Länge [math]l[\math] konstant ist. | ||
| − | Wenn die Nadel nun zwischen zwei Linien liegt, dann können wir für den Abstand [math]y[/math] von einer Linie folgende Relation aufstellen: Für [math]y > sin(φ) | + | Wenn die Nadel nun zwischen zwei Linien liegt, dann können wir für den Abstand [math]y[/math] von einer Linie folgende Relation aufstellen: Für [math]y > sin(φ) \cdot l[/math] ergibt es keinen Schnittpunkt, andernfalls schon. |
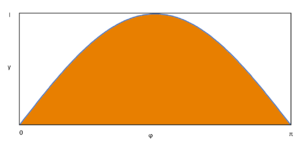
| − | [[Datei:Graphische Darstellung.png|mini | + | [[Datei:Graphische Darstellung.png|mini|Die graphische Darstellung]] |
Wenn wir jetzt graphisch alle möglichen Längen von [math]y[/math] auf der Y-Achse und Winkel φ von 0 bis π auf der X-Achse darstellen, erhalten wir ein Rechteck, bei dem jeder Punkt eine mögliche Lage der Nadel repräsentiert. | Wenn wir jetzt graphisch alle möglichen Längen von [math]y[/math] auf der Y-Achse und Winkel φ von 0 bis π auf der X-Achse darstellen, erhalten wir ein Rechteck, bei dem jeder Punkt eine mögliche Lage der Nadel repräsentiert. | ||
| − | <nowiki>Durch den Zusammenhang [math]y > sin(φ) | + | <nowiki>Durch den Zusammenhang [math]y > sin(φ) \cdot l[/math] können wir ableiten, dass alle Punkte unterhalb der Sinuskurve die untere Achse (also Linie) treffen, alle oberhalb davon nicht. Somit ergibt sich für die Wahrscheinlichkeit [math]p[/math] der Zusammenhang: [math]p=\frac{\mbox{Fläche der Sinuskurve}}{\mbox{Fläche des Rechtecks}}[/math], also [math]p=\frac{\int\limits_{0}^{π}sin(φ)\cdot l}{l\cdot π}=\frac{-cos(π)\cdot l+cos(0)\cdot l}{l\cdot π}=\frac{l+l}{l\cdot π}=\frac{2\cdot l}{l\cdot π}=\frac{2}{π}[/math]</nowiki> |
Somit lässt sich durch experiementelle Bestimmung der Wahrscheinlichkeit [math]\pi[/math] als [math]\pi=\frac{2}{p}[/math] bestimmen. | Somit lässt sich durch experiementelle Bestimmung der Wahrscheinlichkeit [math]\pi[/math] als [math]\pi=\frac{2}{p}[/math] bestimmen. | ||
| Zeile 148: | Zeile 148: | ||
=== Trivia === | === Trivia === | ||
Wenn Ihnen dieser Artikel gefallen hat, könnte Ihnen auch das [[Museumswächterproblem]] gefallen. ^^ | Wenn Ihnen dieser Artikel gefallen hat, könnte Ihnen auch das [[Museumswächterproblem]] gefallen. ^^ | ||
| + | |||
| + | == Autoren == | ||
| + | Rico Görlach, Daniela Müller-Trefzer, Laura Schröpfer, Marcel Stoklasa | ||
Aktuelle Version vom 13. April 2021, 09:35 Uhr
Allgemeines
Die Zahl [math] \pi [/math] ist eine der bekanntesten irrationalen Zahlen und beschreibt zum Beispiel das Verhältnis zwischen Durchmesser und Umfang eines Kreises. Interessanterweise wurde der griechische Buchstabe [math]\pi[/math] (für [math]\pi\varepsilon\rho\iota\varphi\varepsilon\rho\varepsilon\iota\alpha[/math] oder auch peripheria, Randbereich oder [math]\pi\varepsilon\rho\iota\mu\varepsilon\tau\rho o\zeta [/math], auch permetros, Umfang) erst im 17. Jahrhundert durch den englischen Mathematiker William Oughtred erstmals verwendet, verschwand dann wieder und wurde 1737 von Euler wiederentdeckt, erst seit ihm wird [math]\pi[/math] der allgemein verwendete Name für die Kreiszahl.
Als letztere war [math]\pi[/math] allerdings bereits im alten Ägypten, auf etwa [math]\pi = 3,16[/math] genähert, bekannt. Sogar in der Bibel wird [math]\pi[/math],von den Babylonieren auf einen Wert von etwa 3 genähert, erwähnt. Für diese Zahlenwerte ist allerdings leider keine Herkunft bekannt.
Die erste Herleitung gelang Archimedes (287-212 v.Chr.), weshalb die Kreiszahl auch den Namen Archimedes-Konstante erhielt. Archimedes schachtelte hierfür 96-Ecke und bestimmte [math]\pi[/math] so auf zwei Nachkommastellen genau.
Im Mittelalter wurde es in Europa dunkel um [math]\pi[/math], umso mehr lohnt es sich aber, sich China zuzuwenden, wo Zu Chogzhi beeindruckende 7 Nachkommastellen der Kreiszahl bestimmte und das bereits im Jahr 480 n.Chr.. Dem persische Astronom Al-Khashi gelangen im Jahr 1430 sogar 16. In Europa kam der berühmte Fibonacchi 1220 auf gerade mal 3 Stellen.
Dafür gelang es Ludolph van Ceulen 1615 [math]\pi[/math] auf 35 Nachkommastellen genau zu bestimmen. Diese wurden erst nach seinem Tod 1615 veröffentlicht, auf dessen Grabstein graviert, erfährt [math]\pi[/math] hier wohl eine der beeindruckensten Ehrungen und durch ihn auch den Namen der Ludolph'schen Zahl. Die bis dahin beste Näherung von [math]\pi[/math] lieferte im 17. Jahrhundert Christoph Grienberger mit 38 Nachkommastellen - wofür ein [math]10^{40}[/math]-Eck vonnöten war. Dies ist die genaueste Bestimmung der Kreiszahl über Polygone.
Mit der nach John-Machin benannten Formel erreichte dieser 1707 ganze 100 Nachkommastellen, Johann Dase 1844 sogar 200. Sein Rekord wurde nur elf Jahre später von Richter mit 500 Nachkommastellen abgelöst. Den Rekord für die Berechnung per Hand stellte William Shanks mit 707 Stellen nach dem Komma auf - ein Fehler, ab der 528. Stelle hatte er sich verrechnet. Dies fiel allerdings erst im 20 Jahrhundert auf, als Algorithmen zur Bestimmung der Kreiszahl aufkamen.\\ Mit der heutigen Technik muss niemand mehr [math]\pi[/math] per Hand ausrechnen, mit den aktuellen Rekorden würde die Berechnung dafür zu lange dauern. Am 29. Januar 2020 stellte der Amerikaner Timothy Mullicanden mit 50 Billionen Nachkommastellen (50.000.000.000.000) den "aktuellen" Rekord auf.
Möglichkeiten zur Bestimmung von [math] \pi[/math]
Darstellungen der Kreiszahl
| Name | erfunden von | Genauigkeit | Darstellung |
|---|---|---|---|
| Polygon-Ansatz | Archimedes von Syrakus (250 v.Chr.), später aufgegriffen von sehr vielen Mathematikern, bis Ludolph van Ceulen (1596) | von 3 bis 35 Nachkommastellen | Näherung durch Schachtelung von Vielecken (Archimedes: 96, Ludolph van Ceulen: [math] 2^{96} [/math]-Eck) |
| erste geschlossene Formel | François Viète | exakt | [math] \frac{2}{\pi} = \frac{\sqrt{2}}{2}\frac{\sqrt{2+\sqrt{2}}}{2}\frac{\sqrt{2+\sqrt{2+\sqrt{2}}}}{2}\ddots [/math] |
| Wallissche Produkt | John Wallis | exakt | [math] \frac{\pi}{2} = \frac{2}{1}\frac{2}{3}\frac{4}{3}\frac{4}{5}\frac{6}{5}\frac{6}{7}\frac{8}{7}\frac{8}{9}\ddots [/math] |
| Kettenbruchentwicklung | ?? | [math] 3 + \frac{1}{7+\frac{1}{15+\frac{1}{1+\frac{1}{292+\frac{1}{1+\frac{1}{\ddots}}}}}} [/math] | |
| Kettenbruchentwicklung | John Wallis | [math] \frac{4}{\pi} = 1+ \frac{1^2}{2+\frac{3^2}{2+\frac{5^2}{2+\frac{7^2}{2+\frac{9^2}{\ddots}}}}} [/math] | |
| Reihendarstellung | Gottfried Wilhelm Leibniz (1682) (bzw. indische Mathematiker (?) im 15. Jhd.) | lineare Konvergenz | [math] \frac{\pi}{4} = \sum\limits_{n=0}^{\infty}\frac{(-1)^n}{2n+1} [/math] |
| (Taylor-) Reihenentwicklung des arctan | James Gregory (1670) | [math] \arctan(\theta) = \frac{\theta^1}{1}-\frac{\theta^3}{3}+\frac{\theta^5}{5}-\frac{\theta^7}{7}\pm \ddots [/math] | |
| Riemann'sche <math> \zeta </math> -Funktion | Leonard Euler | [math] \zeta(2) = \frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+\frac{1}{4^2}+\ddots = \frac{\pi^2}{6} [/math] | |
| Kettenbruch | Johann Heinrich Lambert (1770) | [math] \frac{4}{\pi} = 1+\frac{1^2}{3+\frac{2^2}{5+\frac{3^2}{7+\frac{4^2}{9+\frac{5^2}{11+\frac{6^2}{\ddots}}}}}} [/math] | |
| elliptische Funktionen und Modulfunktionen | Srinivasa Ramanujan (1914) | nach zweimaliger Iteration 15 korrekte Nachkommastellen | [math] \frac{1}{\pi} = \frac{\sqrt{8}}{9801}\sum\limits_{n=0}^{\infty}\frac{(4n)!(1103+26390n)}{(n!)^4\cdot 396^{4n}} [/math] |
Algorithmen zur numerischen Bestimmung von [math] \pi [/math]
| Name | entwickelt von | Algorithmus |
|---|---|---|
| BBP - Reihen | Simon Plouffe mit Peter Borwein und David Harold Bailey (1995) | [math] \pi = \sum\limits_{k=0}^\infty \frac{1}{16^k} \left(\frac{4}{8k+1}-\frac{2}{8k+4}-\frac{1}{8k+5}-\frac{1}{8k+6}\right) [/math]
[math]\pi = \sum\limits_{k=0}^{\infty} \frac{(-1)^k}{4^k}\left(\frac{2}{4k+1}+\frac{2}{4k+2}+\frac{1}{4k+3}\right) [/math] |
| Tröpferlalgorithmus (lemniskatische Konstante) | Gauß | [math] \frac{1}{\pi} = \text{AGM}\left(1, \sqrt{2}\right)\int\limits_0^1\frac{2dx}{\sqrt{1-x^4}} [/math]
[math] \pi = \frac{4\text{AGM}\left(1, \frac{1}{\sqrt{2}}\right)^2}{1-\sum\limits_{j=1}^{\infty} 2^{j+1}c_j^2} [/math] |
Geometrische Verfahren zur Bestimmung von [math]\pi[/math]
| Name | Verfahren |
|---|---|
| Flächenformel | Betrachte die Fläche eines Kreises [math] A_K = \pi r^2 [/math] und den eines Quadrates mit Seitenlänge [math] 2r[/math] [math]A_Q = (2r)^2 [/math]
Dann ist [math] \frac{A_K}{A_Q} = \frac{\pi}{4}[/math] und [math]\pi = 4\frac{A_K}{A_Q}[/math] Dies lässt sich mit einem Algorithmus ausführen, der ein Quadrat mit einem Raster überdeckt und überprüft, ob ein Rasterabteil auch im Kreis liegt oder nicht. |
| Streifenmethode | Teile hierfür den Kreis in schmale Streifen mit [math] y = \pm\sqrt{r^2-x^2}[/math] und verwende [math] \pi = \frac{A_K}{r^2} [/math] sowie [math] \pi = \int\limits_{-1}^{1}2\sqrt{1-x^2}dx [/math].
Auch dies lässt sich mit einem Algorithmus ausführen. |
| Statistische Bestimmung: Monte-Carlo-Algorithmus | Es wird wieder die Flächenformel [math] \frac{A_K}{A_Q} = \frac{\pi}{4} [/math] verwendet.
Es werden zufällige Punkte auf das Quadrat "regnen" gelassen und jeweils bestimmt, ob der Punkt auch innerhalb des Kreises liegt. Es ergibt sich wieder ein Verhältnis von [math] \frac{\pi}{4} [/math]. Bei dieser Methode muss eine Unsicherheit berücksichtigt werden, wobei diese mit wachsender Zahl der betrachteten Punkte kleiner wird. |
| Physikalisch - Experimentelle Konstruktion | Ein Zylinder mit Radius [math]r = 1[/math] wird bis in eine Höhe von [maht]h_{GZ} \approx 1[/math] mit Wasser gefüllt. Das Wasser wird dann in einen Quader mit Grundfläche [math] a = 1 [/math] umgefüllt.
In Volumeneinheiten ist die Wassermenge im Zylinder [math] V_Z = r^2\pi h_Z = \pi [/math] sowie im Quader [math] V_Q = h_Q [/math], also [math]h_Q = \pi [/math] |
| Buffon'sches Nadelproblem | Thema dieses Wiki-Artikels! |
Graphische Herleitung des Zusammenhangs mit Pi
Um bei dem Buffon'schen Nadelproblem [math]\pi[/math] zu bestimmen, lassen wir Nadeln auf ein Blatt Papier fallen. Auf dem Blatt sind mehrere horizontale (und zueinander parallele) Linien mit frei wählbaren Abstand. Auf dieses Blatt werden nun Nadeln oder ähnliche Objekte fallen gelassen und die Anzahl der Schnittpunkte zwischen den Nadeln und den Linien bestimmt. Wie hoch ist die Wahrscheinlichkeit, einen solchen Schnittpunkt zu erreichen? Für unseren Versuch haben wir die Länge der Nadeln und den Abstand der Linien gleich groß gewählt.
Wir stellen uns vor, die Nadel lässt sich durch einen Anfangspunkt sowie einen Winkel φ beschreiben, da ihre Länge [math]l[\math] konstant ist.
Wenn die Nadel nun zwischen zwei Linien liegt, dann können wir für den Abstand [math]y[/math] von einer Linie folgende Relation aufstellen: Für [math]y > sin(φ) \cdot l[/math] ergibt es keinen Schnittpunkt, andernfalls schon.
Wenn wir jetzt graphisch alle möglichen Längen von [math]y[/math] auf der Y-Achse und Winkel φ von 0 bis π auf der X-Achse darstellen, erhalten wir ein Rechteck, bei dem jeder Punkt eine mögliche Lage der Nadel repräsentiert.
Durch den Zusammenhang [math]y > sin(φ) \cdot l[/math] können wir ableiten, dass alle Punkte unterhalb der Sinuskurve die untere Achse (also Linie) treffen, alle oberhalb davon nicht. Somit ergibt sich für die Wahrscheinlichkeit [math]p[/math] der Zusammenhang: [math]p=\frac{\mbox{Fläche der Sinuskurve}}{\mbox{Fläche des Rechtecks}}[/math], also [math]p=\frac{\int\limits_{0}^{π}sin(φ)\cdot l}{l\cdot π}=\frac{-cos(π)\cdot l+cos(0)\cdot l}{l\cdot π}=\frac{l+l}{l\cdot π}=\frac{2\cdot l}{l\cdot π}=\frac{2}{π}[/math]
Somit lässt sich durch experiementelle Bestimmung der Wahrscheinlichkeit [math]\pi[/math] als [math]\pi=\frac{2}{p}[/math] bestimmen.
Experimentelle Bestimmung von [math]\pi[/math] durch das Nadelproblem
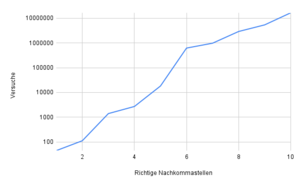
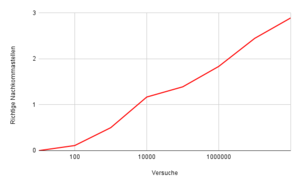
Da die Lösung des Buffon'schen Nadelproblems [math]\pi[/math] enthält, lässt es sich damit experimentell bestimmen. Leider muss man feststellen, das es im Vergleich zu anderen Verfahren sehr langsam gegen [math]\pi[/math] konvergiert. So braucht es im Schnitt ca. 10.000.000 Versuche bis man zum ersten Mal zehn richtige Nachkommastellen bekommt. Betrachtet man das Experiment von der anderen Seite und überprüft wie viele Stellen nach 10,100,1000,... Versuchen korrekt sind, sieht man wie langsam man sich [math]\pi[/math] damit tatsächlich annähert. Selbst bei 100.000.000 Versuchen sind drei richtige Nachkommastellen nicht garantiert und bei all diesen Experimenten gab es maximal fünf richtige Nachkommastellen.
Trivia
Wenn Ihnen dieser Artikel gefallen hat, könnte Ihnen auch das Museumswächterproblem gefallen. ^^
Autoren
Rico Görlach, Daniela Müller-Trefzer, Laura Schröpfer, Marcel Stoklasa