Cantor-Menge: Unterschied zwischen den Versionen
| (337 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | Die Cantor-Menge heißt auch Cantormenge, Wischmenge, Cantorsches Diskontinuum oder Cantor-Staub und ist eine iterativ konstruierte Teilmenge der reellen Zahlen mit besonderen Eigenschaften. | ||
| + | |||
= Georg Cantor - eine Vorstellung = | = Georg Cantor - eine Vorstellung = | ||
| − | Georg Ferdinand Ludwig Philipp Cantor (geboren am 3. März 1845 | + | Georg Ferdinand Ludwig Philipp Cantor (geboren am 3. März 1845 in Sankt Petersburg und gestorben am 6. Januar 1918 in Halle an der Saale) war ein deutscher Mathematiker. |
| − | Er war Kind des | + | Er war Kind des Kaufmanns und Börsenmaklers Georg Woldemar Cantor und Marie Cantor. |
=== Mathematischer Werdegang === | === Mathematischer Werdegang === | ||
| − | Cantor schloss die Schule 1860 mit Auszeichnung an der Realschule Darmstadt ab. | + | Cantor schloss die Schule 1860 mit Auszeichnung an der Realschule Darmstadt ab. Danach besuchte er die Höhere Gewerbeschule Darmstadt, heute die TU Darmstadt, wo er durch den Willen seines Vaters eine Berufsausbildung zum Ingenieur begann. Cantors Stärken aber lagen in der Mathematik und 1862 begann er ein Mathematikstudium am Polytechnikum in Zürich, wobei er 1863 an die Universität Berlin wechselte. 1866 studierte er ein Sommersemester in Göttingen und 1867 wurde er an der Universität Berlin bei Ernst Eduard Kummer promoviert. |
Zu seinen Lehrern zählen die bekannten Mathematiker Karl Weierstraß, Ernst Eduard Kummer und Leopold Kronecker. | Zu seinen Lehrern zählen die bekannten Mathematiker Karl Weierstraß, Ernst Eduard Kummer und Leopold Kronecker. | ||
| − | Nach seinem Studium arbeitete Cantor als Mathematiklehrer am Friedrich-Wilhelm Gymnasium in Berlin. Bereits dort litt er an Depressionen. 1869 habilitierte er | + | Nach seinem Studium arbeitete Cantor als Mathematiklehrer am Friedrich-Wilhelm Gymnasium in Berlin. Bereits dort litt er an Depressionen. 1869 habilitierte er mit dem Thema "De transformatione formarum ternarium quadricarum" an der Universität Halle, wo er bis zum Ende seines Lebens lehrte und arbeitete. Vorab arbeitete er dort als Privatdozent, ab 1872 als Extraordinarius und ab 1877 bis zu seinem Ruhestand 1913 als ordentlicher Professor. |
=== Werk und Leben === | === Werk und Leben === | ||
| Zeile 15: | Zeile 17: | ||
Im Jahre 1870 gelang es ihm, eine Funktion als Summe trigonometrischer Reihen darzustellen. Ab 1872 veröffentlichte er weitere Arbeiten über trigonometrische Reihen. | Im Jahre 1870 gelang es ihm, eine Funktion als Summe trigonometrischer Reihen darzustellen. Ab 1872 veröffentlichte er weitere Arbeiten über trigonometrische Reihen. | ||
1873 folgte der Beweis, dass die rationalen Zahlen abzählbar sind und somit eine Bijektion zwischen den natürlichen Zahlen und den rationalen Zahlen existiert. (1. Cantorsches Diagonalargument). 1874 zeigte er über das 2. Cantorsche Diagonalargument, dass die reellen Zahlen überabzählbar sind. | 1873 folgte der Beweis, dass die rationalen Zahlen abzählbar sind und somit eine Bijektion zwischen den natürlichen Zahlen und den rationalen Zahlen existiert. (1. Cantorsches Diagonalargument). 1874 zeigte er über das 2. Cantorsche Diagonalargument, dass die reellen Zahlen überabzählbar sind. | ||
| − | 1877 beschäftigte er sich mit den geometrischen Anwendungen der Mengenlehre. Er ist beispielsweise von der Annahme ausgegangen, dass ein Quadrat der Seitenlänge 1 nicht genauso viele Elemente enthält, wie eine Linie zwischen 0 und 1. Als er herausfand, dass dem doch so ist, war er von seiner Entdeckung und Beweisführung überrascht. Er schrieb deshalb „Ich sehe es, aber ich glaube es nicht“. Seine neue Entdeckung hatte großen Einfluss auf die bisherigen geometrischen Anschauungen. Seine Abhandlungen zu dem Thema wurden von Leopold Kronecker, der dem Begriff der Unendlichkeit kritisch gegenüberstand, zurückgehalten und erst die Intervention seines Freundes Dedekind führten zur Veröffentlichung. | + | 1877 beschäftigte er sich mit den geometrischen Anwendungen der Mengenlehre. Er ist beispielsweise von der Annahme ausgegangen, dass ein Quadrat der Seitenlänge 1 nicht genauso viele Elemente enthält, wie eine Linie zwischen 0 und 1. Als er herausfand, dass dem doch so ist, war er von seiner Entdeckung und Beweisführung überrascht. Er schrieb deshalb „Ich sehe es, aber ich glaube es nicht“. Seine neue Entdeckung hatte großen Einfluss auf die bisherigen geometrischen Anschauungen. Seine Abhandlungen zu dem Thema wurden von Leopold Kronecker, der dem Begriff der Unendlichkeit kritisch gegenüberstand, zurückgehalten und erst die Intervention seines Freundes Richard Dedekind führten zur Veröffentlichung. |
Von 1879 bis 1884 gab er die Artikelreihe mit dem Namen „Über unendliche lineare Punktmannigfaltigkeiten“ heraus, in der er die Grundlagen und Hauptsätze der Mengenlehre begründete. Seine Erkenntnisse führten zu großem Widerstand, weshalb er fast zehn Jahre lang sein Fachgebiet wechselte und sich vermehrt den Literaturwissenschaften, der Philosophie und der Theologie zuwandt. Seine zweite Lebenshälfte wurde vermehrt von seiner manisch-depressiven Erkrankung geprägt, weshalb er sich in psychiatrische Behandlung begeben musste. | Von 1879 bis 1884 gab er die Artikelreihe mit dem Namen „Über unendliche lineare Punktmannigfaltigkeiten“ heraus, in der er die Grundlagen und Hauptsätze der Mengenlehre begründete. Seine Erkenntnisse führten zu großem Widerstand, weshalb er fast zehn Jahre lang sein Fachgebiet wechselte und sich vermehrt den Literaturwissenschaften, der Philosophie und der Theologie zuwandt. Seine zweite Lebenshälfte wurde vermehrt von seiner manisch-depressiven Erkrankung geprägt, weshalb er sich in psychiatrische Behandlung begeben musste. | ||
Erst 1895 wandte er sich wieder seinem ursprünglichen Gebiet, der Mengenlehre, zu, nachdem er zunehmend Anerkennung und Wertschätzung für seine Arbeit erhielt. | Erst 1895 wandte er sich wieder seinem ursprünglichen Gebiet, der Mengenlehre, zu, nachdem er zunehmend Anerkennung und Wertschätzung für seine Arbeit erhielt. | ||
1899 musste er sich erneut einem Sanatoriumsaufenthalt unterziehen. Kurz nach dem Aufenthalt verstarb sein jüngster Sohn, weshalb sich Cantors psychische Erkrankung verschlimmerte und ein weiterer Sanatoriumsaufenthalt 1903 folgte. Unter seinen Depressionen litt folglich seine mathematische Arbeit. | 1899 musste er sich erneut einem Sanatoriumsaufenthalt unterziehen. Kurz nach dem Aufenthalt verstarb sein jüngster Sohn, weshalb sich Cantors psychische Erkrankung verschlimmerte und ein weiterer Sanatoriumsaufenthalt 1903 folgte. Unter seinen Depressionen litt folglich seine mathematische Arbeit. | ||
| − | 1913 ging er in Pension. Kurz darauf begann 1914 der erste Weltkrieg. Während diesem litt er an Armut und Mangelernährung. Am 6. Januar 1918 starb Cantor an einer Herzinsuffizienz in dem Sanatorium in Halle, in welchem er sein letztes Lebensjahr verbrachte. | + | 1913 ging er in Pension. Kurz darauf begann 1914 der erste Weltkrieg. Während diesem litt er an Armut und Mangelernährung. Am 6. Januar 1918 starb Cantor an einer Herzinsuffizienz in dem Sanatorium in Halle, in welchem er sein letztes Lebensjahr verbrachte. |
| + | |||
| + | Für weitere Informationen siehe auch: <ref>Fröba, Wassermann: Die bedeutendsten Mathematiker, marix Verlag 2012, Abschnitt Georg Cantor</ref> <ref>Purkert, Walter & Ilgauds, Hans Joachim: Georg Cantor 1845–1918. 1987, S. 79 ff. und S.160.</ref> <ref>https://de.wikipedia.org/wiki/Georg_Cantor (zuletzt aufgerufen: 30.03.2021)</ref> | ||
| + | |||
| + | =Konstruktion der Cantor-Menge= | ||
| + | |||
| + | Man konstruiert die Cantor-Menge <math>C</math> iterativ, indem man vom abgeschlossenen Intervall <math>\displaystyle \left[0, 1\right] </math> das mittlere offene Drittel <math>\displaystyle \left[ \frac{1}{3} ,\frac{2}{3} \right]</math> entfernt und aus den beiden verbleibenden abgeschlossenen Intervallen <math>\displaystyle \left[ 0, \frac{1}{3}\right]</math> und <math>\displaystyle\left[ \frac{2}{3} , 1\right]</math> erneut jeweils deren mittleres offenes Drittel entfernt. Dieser Prozess des Entfernens des mittleren offenen Drittels wird unendlich oft fortgesetzt. Die Elemente, die nach unendlicher Wiederholung des Prozesses nicht entfernt wurden, bilden die Cantor-Menge <math>C</math>. Das bedeutet: | ||
| + | |||
| + | :<math> C_0 :=\left[0,1\right] </math> | ||
| + | :<math> C_1 :=\left[0,\frac{1}{3}\right]∪\left[\frac{2}{3},1\right] </math> | ||
| + | :<math> C_2 :=\left[0,\frac{1}{9}\right]∪\left[\frac{2}{9},\frac{1}{3}\right]∪\left[\frac{2}{3},\frac{7}{9}\right]∪\left[\frac{8}{9},1\right] </math> | ||
| + | :<math> C_3 :=\left[0, \frac{1}{27}\right]∪\left[\frac{2}{27} ,\frac{1}{9}\right]∪\left[\frac{2}{9}, \frac{7}{27} \right]∪\left[\frac{8}{27} ,\frac{1}{3}\right]∪\left[\frac{2}{3},\frac{19}{27}\right]∪\left[\frac{20}{27},\frac{7}{9}\right]∪\left[\frac{8}{9},\frac{25}{27}\right]∪\left[\frac{26}{27},1\right] </math> | ||
| + | |||
| + | |||
| + | :<math>... </math> | ||
| + | :<math> C = \bigcap_{n=0}^\infty C_n = \lim_{n\to\infty} C_n </math> <br> | ||
| + | |||
| + | :<math> \text{,da } C_0 \supset C_1 \supset C_2 \supset ...\supset C_{n-1} \supset C_n</math> | ||
| + | |||
| − | |||
| − | + | Folgendes Bild veranschaulicht den Prozess.<br> | |
| + | <br> | ||
| − | + | [[Datei:Geometrische Veranschaulichung.jpg|400x400px|alternativtext=]] | |
| − | + | Bild erstellt von Christina Tian am 21.03.2021. | |
| − | |||
| − | = | + | = Ternär-Darstellung = |
| − | Der internationale Standard sieht das Dezimalsystem als Zahlensystem vor. Dabei wird ein Zahlenwert dargestellt durch Ziffern 0,1,2,3,4,5,6,7,8,9 mit | + | Der internationale Standard sieht das Dezimalsystem als Zahlensystem vor. Dabei wird ein Zahlenwert dargestellt durch Ziffern 0,1,2,3,4,5,6,7,8,9, die mit ihrem Stellenwert als Zehnerpotenz addiert werden Da bei der Cantor-Menge Intervalle iterativ gedrittelt werden, ist es zielführend sich für die nähere Betrachtung der Menge mit dem Stellenwertsystem zur Basis 3 vertraut zu machen, dem Ternär-System. Dieses sieht die Ziffern 0,1,2 und den Stellenwert als Dreierpotenz vor. Zahlenwerte in Ternär-Darstellung werden mit einem Index 3 gekennzeichnet. Das heißt für x ∈ [0, 1], dem Intervall in dem sich die Cantor-Menge befindet, im: |
*Dezimalsystem: <br> | *Dezimalsystem: <br> | ||
| − | :<math>\displaystyle x = 0,x_1 x_2 x_3 ... = \sum_{i=1}^\infty x_i \frac{1}{10^i} | + | :<math>\displaystyle x = 0,x_1 x_2 x_3 ... = \sum_{i=1}^\infty x_i \frac{1}{10^i} \text{ }; x_i ∈ </math> {0,1,...,9} |
| − | * | + | *Ternärsystem: <br> |
| − | :<math>\displaystyle x = 0,x_1 x_2 x_3 ...= \sum_{i=1}^\infty x_i \frac{1}{3^i} | + | :<math>\displaystyle x = 0,x_1 x_2 x_3 ...= \sum_{i=1}^\infty x_i \frac{1}{3^i} \text{ } ; x_i ∈ </math> {0,1,2} |
Beispiele dazu: | Beispiele dazu: | ||
| Zeile 50: | Zeile 69: | ||
| − | So wie im Dezimalsystem | + | So wie im Dezimalsystem <math>\displaystyle 0{,}\overline{9}</math> mit 1 gleichzusetzten ist, gilt dies analog für <math>\displaystyle 0{,}\overline{2}</math> im Ternärsystem. Daraus folgt: |
| − | |||
:<math>\displaystyle (0{,}\overline{2})_3 = 1</math> <br> | :<math>\displaystyle (0{,}\overline{2})_3 = 1</math> <br> | ||
| Zeile 61: | Zeile 79: | ||
| − | Angewandt auf die Cantor-Menge bedeutet das, da das mittlere Intervall mit einer 1 als Stellenwert herausgenommen wird, dass die Menge | + | Angewandt auf die Cantor-Menge bedeutet das, da das mittlere Intervall mit einer 1 als Stellenwert immer wieder herausgenommen wird, dass die Menge <math>C_n</math> aus Elementen besteht, die innerhalb der ersten n-Nachkommastellen in Tenär-Darstellung nur aus den Ziffern 0 und 2 bestehen. Das erleichtert die Zuordnung. Das heißt: |
| − | + | ||
| − | :<math> | + | <math> C_1 :=[0,\frac{1}{3}]∪[\frac{2}{3},1] </math> |
| + | :<math> = [0,(0,1)_3]∪[(0,2)_3,1] </math> | ||
| + | :<math>= [0,(0{,}0\overline{2})_3]∪[(0,2)_3,1]</math><br> | ||
| + | |||
| + | <math> C_2 :=[0,\frac{1}{9}]∪[\frac{2}{9},\frac{1}{3}]∪[\frac{2}{3},\frac{7}{9}]∪[\frac{8}{9},1] </math> | ||
| + | :<math> = [0,(0,01)_3]∪[(0,02)_3,(0,1)_3]∪[(0,2)_3,(0,21)_3]∪[(0,22)_3,1]</math> | ||
| + | :<math> = [0,(0{,}00\overline{2})_3]∪[(0,02)_3,(0{,}0\overline{2})_3]∪ | ||
| + | [(0,2)_3,(0{,}20\overline{2})_3]∪[(0,22)_3,(0{,}\overline{2})_3]</math> <br> | ||
| + | ... | ||
| + | |||
| + | <math> C_n= </math> { <math> x ∈ [0,1]| x_i ∈ </math> {<math> 0,2 </math> } für alle <math> i ≤ n </math> }.<br><br> | ||
| + | Siehe <ref>Appell, Jürgen “Analysis in Beispielen und Gegenbeispielen. Eine Einführung in die Theorie reeller Funktionen”. Springer, Berlin u. a. 2009, ISBN 978-3-540-88902-1, S. 233–237</ref>, <ref>Schilling, Anna (2021) : Cantor-Menge https://mampf.mathi.uni-heidelberg.de/mediaforward/medium/17786/manuscript/db62c69225719ba1d5495987b3d47991.pdf (letzter Zugriff 20.03.2021)</ref>. Bild erstellt von Christina Tian | ||
| + | |||
| + | [[Datei:Cantormenge .jpg|mini|400x400px|Ternär-Darstellung|alternativtext=|links]]<br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
| + | <br> | ||
= Cantorfunktion = | = Cantorfunktion = | ||
| − | Mit Hilfe der | + | Mit Hilfe der Cantor-Menge ''C'' lässt sich rekursiv die sogenannte Cantorfunktion (auch “Teufelstreppe”) definieren. |
| − | + | Wir konstruieren die Cantorfunktion <math> f: \left[0,1\right] -> \left[0,1\right] </math> mit <math>f(0) = 0 </math> und <math>f(1) = 1</math> folgendermaßen:<br> | |
| − | * Drücke x in Basis 3 approximiert aus | + | Sei <math> x ∈ \left[0,1\right]</math>, dann erhalten wir die Cantorfunktion <math>f(x)</math> durch die folgenden Schritte: |
| − | * Wenn x eine 1 enthält, ersetze jede Ziffer streng nach der ersten 1 durch 0. | + | * Drücke <math>x</math> in Basis 3 approximiert aus |
| + | * Wenn <math>x</math> eine 1 enthält, ersetze jede Ziffer streng nach der ersten 1 durch 0. | ||
* Ersetze alle verbleibenden 2en durch 1en. | * Ersetze alle verbleibenden 2en durch 1en. | ||
* Interpretiere das Ergebnis als Binärzahl. | * Interpretiere das Ergebnis als Binärzahl. | ||
| − | Der Graph der Funktion ist durch folgendes Bild veranschaulicht. | + | Der Graph der Funktion ist durch folgendes Bild veranschaulicht.<ref>Bildnachweis https://de.wikipedia.org/wiki/Cantor-Verteilung#/media/Datei:Cantor-Funktion.svg (letzter Zugriff 20.03.2021)</ref><br> |
| − | + | <br> | |
| + | <br> | ||
| + | <br> | ||
| − | |||
| − | + | [[Datei:Graph der Cantofunktion.jpg|500x500px|alternativtext=]] | |
| − | + | Die Teufelstreppe <math> f </math> ist monoton steigend und in allen Punkten <math> x ∈ \left[0,1\right] </math> \ <math> C </math> differenzierbar mit der Ableitung 0, da sie dort konstant ist. In den Elementen der Cantormenge wie zum Beispiel 0 und 1 und den Randpunkten der entfernten Drittelintervalle ist <math> f </math> nicht differenzierbar. | |
| − | + | Sie steht in Bezug mit einer besonderen Wahrscheinlichkeitsverteilung. Siehe <ref>Deiser, Oliver :Einführung in die Mengenlehre https://www.aleph1.info/?call=Puc&permalink=mengenlehre1_4_3 S.530-544 (letzter Zugriff 25.03.2021)</ref>, <ref>Fleron, Julian F. “A Note on the History of the Cantor Set and Cantor Function.” Mathematics Magazine, vol. 67, no. 2, 1994, pp. 136–140. JSTOR, https://www.jstor.org/stable/2690689 (letzter Zugriff 18.03.2021)</ref>, <ref>https://wiki.math.ntnu.no/_media/tma4225/2015h/cantor_set_function.pdf (letzter Zugriff 26.03.2021)</ref> | |
| − | |||
| − | + | = Eigenschaften = | |
| − | + | 1884 veröffentlicht Cantor sein Werk ''Über unendliche, lineare Punktmannigfaltigkeiten (VI)''. Im Paragraphen § 19 beschäftigt er sich mit perfekten (siehe unten) Teilmengen von ℝ. | |
| − | + | Hierzu verwendet er die Cantormenge und zeigt, dass jede beschränkte nichtleere perfekte Teilmenge von ℝ, die keine nichttrivialen Intervalle enthält, ähnlich ist zur Cantor-Menge <math>C</math>. Siehe <ref>Deiser, Oliver :Einführung in die Mengenlehre https://www.aleph1.info/?call=Puc&permalink=mengenlehre1_4_3 S.530-544 (letzter Zugriff 25.03.2021)</ref>, <ref>Fleron, Julian F. “A Note on the History of the Cantor Set and Cantor Function.” Mathematics Magazine, vol. 67, no. 2, 1994, pp. 136–140. JSTOR, https://www.jstor.org/stable/2690689 (letzter Zugriff 18.03.2021)</ref>, <ref>H. Amann, J. Escher: Analysis I</ref>.<br> | |
| − | + | <br> | |
| − | |||
| − | |||
| + | In der Tat hat die Cantormenge <math>C</math> besondere Eigenschaften: | ||
| − | + | * <math>C</math> ist kompakt. | |
| − | + | * <math>C</math> hat keine isolierte Punkte. | |
| − | + | * <math>C</math> hat Länge 0. | |
| − | + | * <math>C</math> ist total unzusammenhängend und hat ein leeres Inneres. | |
| + | * <math>C</math> ist überabzählbar. | ||
| − | === | + | === Kompaktheit <ref>Schilling, Anna (2021) : Cantor-Menge https://mampf.mathi.uni-heidelberg.de/mediaforward/medium/17786/manuscript/db62c69225719ba1d5495987b3d47991.pdf (letzter Zugriff 20.03.2021)</ref> === |
| + | Da die Cantor-Menge <math>C</math> eine Teilmenge der Reelen Zahlen <math>\mathbb R</math> ist, gilt der Satz von Heine-Borel, sodass Mengen genau dann kompakt sind, wenn sie abgeschlossen und beschränkt sind. <br> | ||
| + | Abgeschlossenheit:<br>Cantor-Menge <math>C</math> abgeschlossen <math>\Leftrightarrow </math> Komplement <math>\mathbb R</math> \C offen | ||
| + | :<math>\mathbb R</math> \<math>C</math> = <math>\mathbb R</math> \<math>[0, 1] ∪\bigcup_{i\in \mathbb N} I_i </math> ,wobei <math> I</math> die herausgenommenem offenen Intervalle sind | ||
| + | Innerhalb der reellen Zahlen ist die beliebige Vereinigung offeneren Mengen stets offen, deswegen <math>\mathbb R</math> \<math>C</math> offen und somit | ||
| + | <math>C</math> abgeschlossen. | ||
| − | + | Beschränktheit:<br> | |
| + | Die Cantormenge ist als Teilmenge des beschränkten Intervalls <math>[0, 1]</math> ebenfalls beschränkt.<br> | ||
| + | Damit besitzt die Cantor-Menge die topologische Eigenschaft der Kompaktheit.<br> | ||
| − | |||
| − | === Länge === | + | === Länge <ref>https://mampf.mathi.uni-heidelberg.de/mediaforward/medium/17423/manuscript/b53706c913236535b9c57ba1da7e7eb4.pdf</ref> === |
| + | |||
| + | Die Menge <math>C_n</math> besteht aus 2<sup>n</sup> Intervallen der Länge [math](\frac{1}{3^n}) [/math]. Folglich ist die Gesamtlänge von <math>C_n</math> ,<br> | ||
| + | :[math]|C_n| = 2^n * (\frac{1}{3^n}) = (\frac{2}{3})^n [/math]<br> | ||
| + | Um die Gesamtlänge <math>|C|</math> der Cantor-Menge zu erhalten, betrachtet man nun den Limes: lim<sub>n→∞</sub> [math]((\frac{2}{3})^n) [/math]. <br> | ||
| + | Da [math]|(\frac{2}{3})| < 1 [/math] ist, handelt es sich um eine Nullfolge, somit gilt: |C| = 0. <br> | ||
| + | Die Länge der Cantor-Menge beträgt also 0. | ||
| − | + | === Inneres <ref>Wiegand, Kevin (2021): https://mampf.mathi.uni-heidelberg.de/mediaforward/medium/17423/manuscript/b53706c913236535b9c57ba1da7e7eb4.pdf (zuletzt aufgerufen: 30.03.2021)</ref> === | |
| + | |||
| + | Die Mengen <math> C_n, n\in \mathbb N </math>, können als die Vereinigung von 2<sup>n</sup> disjunkten, abgeschlossenen Intervallen I<sub>n,k</sub> mit Länge [math](\frac{1}{3^n}) [/math] dargestellt werden. Es gilt also: | ||
| + | :<math> C_n = \bigcup_{k\in \mathbb N} I_{n,k}.</math> | ||
| − | === | + | Behauptung: Das Innere C° der Cantor-Menge C ist leer: C° = ∅. |
| + | |||
| + | Beweis der Behauptung per Widerspruch: | ||
| + | |||
| + | Annahme: Es existiert ein x ∈ C°, also gibt es ein ε > 0 mit (x−ε,x+ε) ⊂ C° ⊂ C. Dann gilt auch für alle ''n ∈ N'', dass (x−ε,x+ε) ⊂ ''Cn''. Die Gesamtlänge von ''Cn'' erfüllt also <math> 2ε ≤ \sum_{k=1}^{2n} |I_{n,k} | = \frac {2^n}{3^n}=(\frac{2}{3})^n </math>. <br> | ||
| + | Dies widerspricht jedoch der oben bewiesenen Konvergenz der Länge gegen 0. (s.o. Länge). | ||
| − | + | === Total unzusammenhängend === | |
| + | |||
| + | Die Cantor-Menge ist total unzusammenhängend, was bedeutet, dass es neben der leeren Menge und den einelementigen Mengen keine weiteren zusammenhängenden Mengen gibt. <br> | ||
| + | Zu zeigen ist also, dass<br> | ||
| + | :<math>∀a,b ∈ C</math>: <math> \text{ }a<b \text{ }∃ \text{ }r ∈ \text{ }\mathbb R</math>\ <math>C:a<r<b</math> | ||
| + | |||
| + | Sei also nun <math>a<b</math>. Dann gilt insbesondere <math> a≠b</math> . Damit folgt: | ||
| + | :<math>∃k ∈\mathbb N</math> minimal <math>: a_k ≠ b_k</math>, wobei <math>a_k</math> und <math>b_k</math> Nachkommastellen von a und b in der Ternär-Darstellung sind. <br> | ||
| + | Nun lässt sich also ein <math> r ∈ \mathbb R</math> \<math> C : a<r<b </math> konstruieren. <br> | ||
| − | + | Wir definieren <math> r:= 0,a_1...a_{k-1}11</math>. <br> | |
| + | (Die zweite 1 muss hinzugefügt werden, da gilt <math>...x_j10000... = ....x_j0222... </math> womit <math>r</math> sonst nach Ternär-Darstellung in der Cantor-Menge liegt) Somit gilt also <math> r_k≠a_k </math> und <math> r_k≠b_k</math>, da nach der Ternär-Darstellung gilt, dass alle Nachkommastellen den Wert 0 oder 2 annehmen. Es folgt, da <math> a<b</math> und <math>a_k ≠ b_k: a_k ≠ r_k ≠ b_k </math>. | ||
| + | Nach Konstruktion gilt also <math> a<r<b </math> und <math> r ∈ \mathbb R</math> \<math>C</math>. <br> | ||
| + | Damit ist die Behauptung bewiesen. | ||
| + | Deshalb wird <math>C</math> auch ''Cantorsches Diskontinuum'' genannt. | ||
| − | + | === Perfektheit === | |
| + | |||
| + | Sei <math>M</math> ein topologischer Raum, eine Teilmenge <math> A ⊂ M </math> heißt perfekt, wenn A kompakt ist und keine isolierte Punkte besitzt. Ein Punkt <math>p</math> heißt isoliert, falls es eine Umgebung um <math>p</math> gibt, die <math>p</math> als einzigen Punkt enthält. | ||
| + | |||
| + | Wie schon erwähnt, ist die Cantormenge eine solche Menge (Vgl: ''C'' total unzusammenhängend). | ||
| + | === Kardinalität === | ||
| + | Durch das [https://de.wikipedia.org/wiki/Cantors_zweites_Diagonalargument 2. Cantorsche Diagonalverfahren] lässt sich beweisen, dass die Cantor-Menge überabzählbar ist. Seien dazu <math> c_1, c_2, c_3 </math> Elemente der Cantor-Menge. | ||
| + | |||
| + | Folgendes Bild veranschaulicht das Verfahren, an einem Beispiel.<br> | ||
| − | = | + | [[Datei:2. Cantorsches Verfahren - Veranschaulichung.jpg|alternativtext=|498x498px]]<br> |
| + | <br> <br> | ||
| + | Bild erstellt von Matilde Sciortino am 29.März 2021 | ||
| + | Damit ist die Cantor-Menge gleichmächtig zum Intervall [0, 1] das ebenfalls, wie alle Intervalle, überabzählbar ist. | ||
| + | = Musikalische Interpretation = | ||
| − | + | Der rumänische Komponist György Ligeti macht in seiner Komposition ''"L'escalier du diable" (''“Die Teufelstreppe”'')'' innerhalb seiner 13. Etüde die Cantor-Funktion musikalisch fühlbar. <ref>https://wiki.math.ntnu.no/_media/tma4225/2015h/cantor_set_function.pdf (letzter Zugriff 26.03.2021)</ref> höre [19]. | |
| − | + | Der endliche Aufstieg des Intervalls [0, 1] in überabzählbar unendlich vielen Schritten ist durch sich selbstähnliche Harmonien illustriert. Die, aufgrund der herausgenommen Intervalle, konstanten Abschnitte der Cantorfunktion sind in Ligetis Werk erkennbar durch Tempi und Dynamik. Die steigende Monotonie der Funktion wird durch ein sich beschleunigendes Tempo in der Komposition ausgedrückt. | |
| + | Ihre Struktur ist analog zur Cantor-Menge dreiteilig. Nach dem ersten musikalischen Intervall wird der mittlere Teil des nächsten Intervall verändert und dann nochmals mit einem veränderten mittleren geteilt. | ||
| − | + | Die Komposition versucht eine Darstellung der unvorstellbaren Unendlichkeit in der Kunst zu geben, was in der Mathematik formal möglich ist. | |
| − | + | = Erdbeben und die Cantorfunktion = | |
| − | |||
| − | = | + | Der Seismologe Yuan Chen und seine Kollegen an der University of Missouri in Columbia haben in einer Studie herausgefunden, dass viele Starkbeben dem zeitlichen Muster der Cantorfunktion folgen. <ref>https://pubs.geoscienceworld.org/ssa/bssa/article-abstract/110/3/1064/583503/Complex-Temporal-Patterns-of-Large-Earthquakes?redirectedFrom=fulltext (letzter Zugriff 30.03.2021)</ref> |
| − | + | Die Forscher haben die zeitliche Abfolge von Starkbeben in Erdbebenzonen an der Plattengrenze zwischen Afrika und Eurasien im Westen Algeriens, im New-Madrid-Erdbebengebiet im Zentrum der USA und in Australien beobachtet. | |
| − | + | „Es sind viele Erdbebensequenzen, die komplex und variabel sind [...] und zeigen Cluster von Ereignissen, die durch lange, aber unregelmäßige Intervalle der Ruhe unterbrochen sind“,<ref>Podbregar, Nadja (2020):"Erdbeben folgen einer 'Teufelstreppe'": https://www.scinexx.de/news/geowissen/erdbeben-folgen-einer-teufelstreppe/ (zuletzt aufgerufen: 31.03.2021)</ref> sagen Yuan Chen und sein Team. | |
| − | |||
| − | Die | + | Wenn man die Häufigkeitsverteilung der Beben in ein Diagramm einträgt, kann man an eine ansteigende Treppe mit verschiedenbreiten Stufen das Muster der Cantorfunktion, erkennen. Die Form der Treppe ist aber von der Region abhängig: Die Länge der Ruheintervalle, also die Breite der „Stufen“ ist mit der im Untergrund aufgestauten Spannung verbunden, je höher die Spannung, desto schmaler die Stufe. |
| − | |||
| − | = Quellen und | + | = Quellen und Bemerkungen = |
| − | |||
<references /> | <references /> | ||
| + | 19. <nowiki>https://youtu.be/uoLam2O3gtY</nowiki> | ||
| + | |||
| + | = Autoren = | ||
| + | |||
| + | Christina Tian, Hannah Pompetzki, Matilde Sciortino, Marianna Hofmeier | ||
Aktuelle Version vom 18. April 2021, 11:27 Uhr
Die Cantor-Menge heißt auch Cantormenge, Wischmenge, Cantorsches Diskontinuum oder Cantor-Staub und ist eine iterativ konstruierte Teilmenge der reellen Zahlen mit besonderen Eigenschaften.
Georg Cantor - eine Vorstellung
Georg Ferdinand Ludwig Philipp Cantor (geboren am 3. März 1845 in Sankt Petersburg und gestorben am 6. Januar 1918 in Halle an der Saale) war ein deutscher Mathematiker. Er war Kind des Kaufmanns und Börsenmaklers Georg Woldemar Cantor und Marie Cantor.
Mathematischer Werdegang
Cantor schloss die Schule 1860 mit Auszeichnung an der Realschule Darmstadt ab. Danach besuchte er die Höhere Gewerbeschule Darmstadt, heute die TU Darmstadt, wo er durch den Willen seines Vaters eine Berufsausbildung zum Ingenieur begann. Cantors Stärken aber lagen in der Mathematik und 1862 begann er ein Mathematikstudium am Polytechnikum in Zürich, wobei er 1863 an die Universität Berlin wechselte. 1866 studierte er ein Sommersemester in Göttingen und 1867 wurde er an der Universität Berlin bei Ernst Eduard Kummer promoviert. Zu seinen Lehrern zählen die bekannten Mathematiker Karl Weierstraß, Ernst Eduard Kummer und Leopold Kronecker. Nach seinem Studium arbeitete Cantor als Mathematiklehrer am Friedrich-Wilhelm Gymnasium in Berlin. Bereits dort litt er an Depressionen. 1869 habilitierte er mit dem Thema "De transformatione formarum ternarium quadricarum" an der Universität Halle, wo er bis zum Ende seines Lebens lehrte und arbeitete. Vorab arbeitete er dort als Privatdozent, ab 1872 als Extraordinarius und ab 1877 bis zu seinem Ruhestand 1913 als ordentlicher Professor.
Werk und Leben
Cantor ist der Begründer der Mengenlehre und prägte den Begriff der Unendlichkeit. Im Jahre 1870 gelang es ihm, eine Funktion als Summe trigonometrischer Reihen darzustellen. Ab 1872 veröffentlichte er weitere Arbeiten über trigonometrische Reihen. 1873 folgte der Beweis, dass die rationalen Zahlen abzählbar sind und somit eine Bijektion zwischen den natürlichen Zahlen und den rationalen Zahlen existiert. (1. Cantorsches Diagonalargument). 1874 zeigte er über das 2. Cantorsche Diagonalargument, dass die reellen Zahlen überabzählbar sind. 1877 beschäftigte er sich mit den geometrischen Anwendungen der Mengenlehre. Er ist beispielsweise von der Annahme ausgegangen, dass ein Quadrat der Seitenlänge 1 nicht genauso viele Elemente enthält, wie eine Linie zwischen 0 und 1. Als er herausfand, dass dem doch so ist, war er von seiner Entdeckung und Beweisführung überrascht. Er schrieb deshalb „Ich sehe es, aber ich glaube es nicht“. Seine neue Entdeckung hatte großen Einfluss auf die bisherigen geometrischen Anschauungen. Seine Abhandlungen zu dem Thema wurden von Leopold Kronecker, der dem Begriff der Unendlichkeit kritisch gegenüberstand, zurückgehalten und erst die Intervention seines Freundes Richard Dedekind führten zur Veröffentlichung. Von 1879 bis 1884 gab er die Artikelreihe mit dem Namen „Über unendliche lineare Punktmannigfaltigkeiten“ heraus, in der er die Grundlagen und Hauptsätze der Mengenlehre begründete. Seine Erkenntnisse führten zu großem Widerstand, weshalb er fast zehn Jahre lang sein Fachgebiet wechselte und sich vermehrt den Literaturwissenschaften, der Philosophie und der Theologie zuwandt. Seine zweite Lebenshälfte wurde vermehrt von seiner manisch-depressiven Erkrankung geprägt, weshalb er sich in psychiatrische Behandlung begeben musste. Erst 1895 wandte er sich wieder seinem ursprünglichen Gebiet, der Mengenlehre, zu, nachdem er zunehmend Anerkennung und Wertschätzung für seine Arbeit erhielt. 1899 musste er sich erneut einem Sanatoriumsaufenthalt unterziehen. Kurz nach dem Aufenthalt verstarb sein jüngster Sohn, weshalb sich Cantors psychische Erkrankung verschlimmerte und ein weiterer Sanatoriumsaufenthalt 1903 folgte. Unter seinen Depressionen litt folglich seine mathematische Arbeit. 1913 ging er in Pension. Kurz darauf begann 1914 der erste Weltkrieg. Während diesem litt er an Armut und Mangelernährung. Am 6. Januar 1918 starb Cantor an einer Herzinsuffizienz in dem Sanatorium in Halle, in welchem er sein letztes Lebensjahr verbrachte.
Für weitere Informationen siehe auch: [1] [2] [3]
Konstruktion der Cantor-Menge
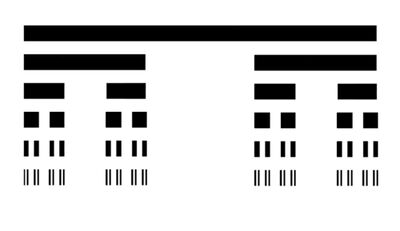
Man konstruiert die Cantor-Menge [math]C[/math] iterativ, indem man vom abgeschlossenen Intervall [math]\displaystyle \left[0, 1\right] [/math] das mittlere offene Drittel [math]\displaystyle \left[ \frac{1}{3} ,\frac{2}{3} \right][/math] entfernt und aus den beiden verbleibenden abgeschlossenen Intervallen [math]\displaystyle \left[ 0, \frac{1}{3}\right][/math] und [math]\displaystyle\left[ \frac{2}{3} , 1\right][/math] erneut jeweils deren mittleres offenes Drittel entfernt. Dieser Prozess des Entfernens des mittleren offenen Drittels wird unendlich oft fortgesetzt. Die Elemente, die nach unendlicher Wiederholung des Prozesses nicht entfernt wurden, bilden die Cantor-Menge [math]C[/math]. Das bedeutet:
- [math] C_0 :=\left[0,1\right] [/math]
- [math] C_1 :=\left[0,\frac{1}{3}\right]∪\left[\frac{2}{3},1\right] [/math]
- [math] C_2 :=\left[0,\frac{1}{9}\right]∪\left[\frac{2}{9},\frac{1}{3}\right]∪\left[\frac{2}{3},\frac{7}{9}\right]∪\left[\frac{8}{9},1\right] [/math]
- [math] C_3 :=\left[0, \frac{1}{27}\right]∪\left[\frac{2}{27} ,\frac{1}{9}\right]∪\left[\frac{2}{9}, \frac{7}{27} \right]∪\left[\frac{8}{27} ,\frac{1}{3}\right]∪\left[\frac{2}{3},\frac{19}{27}\right]∪\left[\frac{20}{27},\frac{7}{9}\right]∪\left[\frac{8}{9},\frac{25}{27}\right]∪\left[\frac{26}{27},1\right] [/math]
- [math]... [/math]
- [math] C = \bigcap_{n=0}^\infty C_n = \lim_{n\to\infty} C_n [/math]
- [math] \text{,da } C_0 \supset C_1 \supset C_2 \supset ...\supset C_{n-1} \supset C_n[/math]
Folgendes Bild veranschaulicht den Prozess.
Bild erstellt von Christina Tian am 21.03.2021.
Ternär-Darstellung
Der internationale Standard sieht das Dezimalsystem als Zahlensystem vor. Dabei wird ein Zahlenwert dargestellt durch Ziffern 0,1,2,3,4,5,6,7,8,9, die mit ihrem Stellenwert als Zehnerpotenz addiert werden Da bei der Cantor-Menge Intervalle iterativ gedrittelt werden, ist es zielführend sich für die nähere Betrachtung der Menge mit dem Stellenwertsystem zur Basis 3 vertraut zu machen, dem Ternär-System. Dieses sieht die Ziffern 0,1,2 und den Stellenwert als Dreierpotenz vor. Zahlenwerte in Ternär-Darstellung werden mit einem Index 3 gekennzeichnet. Das heißt für x ∈ [0, 1], dem Intervall in dem sich die Cantor-Menge befindet, im:
- Dezimalsystem:
- [math]\displaystyle x = 0,x_1 x_2 x_3 ... = \sum_{i=1}^\infty x_i \frac{1}{10^i} \text{ }; x_i ∈ [/math] {0,1,...,9}
- Ternärsystem:
- [math]\displaystyle x = 0,x_1 x_2 x_3 ...= \sum_{i=1}^\infty x_i \frac{1}{3^i} \text{ } ; x_i ∈ [/math] {0,1,2}
Beispiele dazu:
- [math]\displaystyle \frac{1}{3} = (0,1)_3 [/math]
- [math]\displaystyle \frac{2}{3} = \frac{1}{3} + \frac{1}{3} = (0,2)_3 [/math]
- [math]\displaystyle \frac{13}{27} = \frac{1}{3}+\frac{1}{9}+\frac{1}{27}= \frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3} = (0,111)_3 [/math]
So wie im Dezimalsystem [math]\displaystyle 0{,}\overline{9}[/math] mit 1 gleichzusetzten ist, gilt dies analog für [math]\displaystyle 0{,}\overline{2}[/math] im Ternärsystem. Daraus folgt:
- [math]\displaystyle (0{,}\overline{2})_3 = 1[/math]
- [math]\displaystyle(0{,}0\overline{2})_3 =(0,1)_3[/math]
- [math]\displaystyle(0{,}11\overline{2})_3 =(0,12)_3[/math]
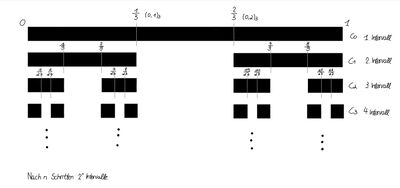
Angewandt auf die Cantor-Menge bedeutet das, da das mittlere Intervall mit einer 1 als Stellenwert immer wieder herausgenommen wird, dass die Menge [math]C_n[/math] aus Elementen besteht, die innerhalb der ersten n-Nachkommastellen in Tenär-Darstellung nur aus den Ziffern 0 und 2 bestehen. Das erleichtert die Zuordnung. Das heißt:
[math] C_1 :=[0,\frac{1}{3}]∪[\frac{2}{3},1] [/math]
- [math] = [0,(0,1)_3]∪[(0,2)_3,1] [/math]
- [math]= [0,(0{,}0\overline{2})_3]∪[(0,2)_3,1][/math]
[math] C_2 :=[0,\frac{1}{9}]∪[\frac{2}{9},\frac{1}{3}]∪[\frac{2}{3},\frac{7}{9}]∪[\frac{8}{9},1] [/math]
- [math] = [0,(0,01)_3]∪[(0,02)_3,(0,1)_3]∪[(0,2)_3,(0,21)_3]∪[(0,22)_3,1][/math]
- [math] = [0,(0{,}00\overline{2})_3]∪[(0,02)_3,(0{,}0\overline{2})_3]∪
[(0,2)_3,(0{,}20\overline{2})_3]∪[(0,22)_3,(0{,}\overline{2})_3][/math]
...
[math] C_n= [/math] { [math] x ∈ [0,1]| x_i ∈ [/math] {[math] 0,2 [/math] } für alle [math] i ≤ n [/math] }.
Siehe [4], [5]. Bild erstellt von Christina Tian
Cantorfunktion
Mit Hilfe der Cantor-Menge C lässt sich rekursiv die sogenannte Cantorfunktion (auch “Teufelstreppe”) definieren.
Wir konstruieren die Cantorfunktion [math] f: \left[0,1\right] -\gt \left[0,1\right] [/math] mit [math]f(0) = 0 [/math] und [math]f(1) = 1[/math] folgendermaßen:
Sei [math] x ∈ \left[0,1\right][/math], dann erhalten wir die Cantorfunktion [math]f(x)[/math] durch die folgenden Schritte:
- Drücke [math]x[/math] in Basis 3 approximiert aus
- Wenn [math]x[/math] eine 1 enthält, ersetze jede Ziffer streng nach der ersten 1 durch 0.
- Ersetze alle verbleibenden 2en durch 1en.
- Interpretiere das Ergebnis als Binärzahl.
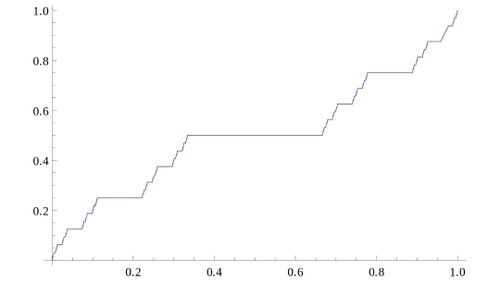
Der Graph der Funktion ist durch folgendes Bild veranschaulicht.[6]
Die Teufelstreppe [math] f [/math] ist monoton steigend und in allen Punkten [math] x ∈ \left[0,1\right] [/math] \ [math] C [/math] differenzierbar mit der Ableitung 0, da sie dort konstant ist. In den Elementen der Cantormenge wie zum Beispiel 0 und 1 und den Randpunkten der entfernten Drittelintervalle ist [math] f [/math] nicht differenzierbar.
Sie steht in Bezug mit einer besonderen Wahrscheinlichkeitsverteilung. Siehe [7], [8], [9]
Eigenschaften
1884 veröffentlicht Cantor sein Werk Über unendliche, lineare Punktmannigfaltigkeiten (VI). Im Paragraphen § 19 beschäftigt er sich mit perfekten (siehe unten) Teilmengen von ℝ.
Hierzu verwendet er die Cantormenge und zeigt, dass jede beschränkte nichtleere perfekte Teilmenge von ℝ, die keine nichttrivialen Intervalle enthält, ähnlich ist zur Cantor-Menge [math]C[/math]. Siehe [10], [11], [12].
In der Tat hat die Cantormenge [math]C[/math] besondere Eigenschaften:
- [math]C[/math] ist kompakt.
- [math]C[/math] hat keine isolierte Punkte.
- [math]C[/math] hat Länge 0.
- [math]C[/math] ist total unzusammenhängend und hat ein leeres Inneres.
- [math]C[/math] ist überabzählbar.
Kompaktheit [13]
Da die Cantor-Menge [math]C[/math] eine Teilmenge der Reelen Zahlen [math]\mathbb R[/math] ist, gilt der Satz von Heine-Borel, sodass Mengen genau dann kompakt sind, wenn sie abgeschlossen und beschränkt sind.
Abgeschlossenheit:
Cantor-Menge [math]C[/math] abgeschlossen [math]\Leftrightarrow [/math] Komplement [math]\mathbb R[/math] \C offen
- [math]\mathbb R[/math] \[math]C[/math] = [math]\mathbb R[/math] \[math][0, 1] ∪\bigcup_{i\in \mathbb N} I_i [/math] ,wobei [math] I[/math] die herausgenommenem offenen Intervalle sind
Innerhalb der reellen Zahlen ist die beliebige Vereinigung offeneren Mengen stets offen, deswegen [math]\mathbb R[/math] \[math]C[/math] offen und somit [math]C[/math] abgeschlossen.
Beschränktheit:
Die Cantormenge ist als Teilmenge des beschränkten Intervalls [math][0, 1][/math] ebenfalls beschränkt.
Damit besitzt die Cantor-Menge die topologische Eigenschaft der Kompaktheit.
Länge [14]
Die Menge [math]C_n[/math] besteht aus 2n Intervallen der Länge [math](\frac{1}{3^n}) [/math]. Folglich ist die Gesamtlänge von [math]C_n[/math] ,
- [math]|C_n| = 2^n * (\frac{1}{3^n}) = (\frac{2}{3})^n [/math]
Um die Gesamtlänge [math]|C|[/math] der Cantor-Menge zu erhalten, betrachtet man nun den Limes: limn→∞ [math]((\frac{2}{3})^n) [/math].
Da [math]|(\frac{2}{3})| < 1 [/math] ist, handelt es sich um eine Nullfolge, somit gilt: |C| = 0.
Die Länge der Cantor-Menge beträgt also 0.
Inneres [15]
Die Mengen [math] C_n, n\in \mathbb N [/math], können als die Vereinigung von 2n disjunkten, abgeschlossenen Intervallen In,k mit Länge [math](\frac{1}{3^n}) [/math] dargestellt werden. Es gilt also:
- [math] C_n = \bigcup_{k\in \mathbb N} I_{n,k}.[/math]
Behauptung: Das Innere C° der Cantor-Menge C ist leer: C° = ∅.
Beweis der Behauptung per Widerspruch:
Annahme: Es existiert ein x ∈ C°, also gibt es ein ε > 0 mit (x−ε,x+ε) ⊂ C° ⊂ C. Dann gilt auch für alle n ∈ N, dass (x−ε,x+ε) ⊂ Cn. Die Gesamtlänge von Cn erfüllt also [math] 2ε ≤ \sum_{k=1}^{2n} |I_{n,k} | = \frac {2^n}{3^n}=(\frac{2}{3})^n [/math].
Dies widerspricht jedoch der oben bewiesenen Konvergenz der Länge gegen 0. (s.o. Länge).
Total unzusammenhängend
Die Cantor-Menge ist total unzusammenhängend, was bedeutet, dass es neben der leeren Menge und den einelementigen Mengen keine weiteren zusammenhängenden Mengen gibt.
Zu zeigen ist also, dass
- [math]∀a,b ∈ C[/math]: [math] \text{ }a\lt b \text{ }∃ \text{ }r ∈ \text{ }\mathbb R[/math]\ [math]C:a\lt r\lt b[/math]
Sei also nun [math]a\lt b[/math]. Dann gilt insbesondere [math] a≠b[/math] . Damit folgt:
- [math]∃k ∈\mathbb N[/math] minimal [math]: a_k ≠ b_k[/math], wobei [math]a_k[/math] und [math]b_k[/math] Nachkommastellen von a und b in der Ternär-Darstellung sind.
Nun lässt sich also ein [math] r ∈ \mathbb R[/math] \[math] C : a\lt r\lt b [/math] konstruieren.
Wir definieren [math] r:= 0,a_1...a_{k-1}11[/math].
(Die zweite 1 muss hinzugefügt werden, da gilt [math]...x_j10000... = ....x_j0222... [/math] womit [math]r[/math] sonst nach Ternär-Darstellung in der Cantor-Menge liegt) Somit gilt also [math] r_k≠a_k [/math] und [math] r_k≠b_k[/math], da nach der Ternär-Darstellung gilt, dass alle Nachkommastellen den Wert 0 oder 2 annehmen. Es folgt, da [math] a\lt b[/math] und [math]a_k ≠ b_k: a_k ≠ r_k ≠ b_k [/math].
Nach Konstruktion gilt also [math] a\lt r\lt b [/math] und [math] r ∈ \mathbb R[/math] \[math]C[/math].
Damit ist die Behauptung bewiesen.
Deshalb wird [math]C[/math] auch Cantorsches Diskontinuum genannt.
Perfektheit
Sei [math]M[/math] ein topologischer Raum, eine Teilmenge [math] A ⊂ M [/math] heißt perfekt, wenn A kompakt ist und keine isolierte Punkte besitzt. Ein Punkt [math]p[/math] heißt isoliert, falls es eine Umgebung um [math]p[/math] gibt, die [math]p[/math] als einzigen Punkt enthält.
Wie schon erwähnt, ist die Cantormenge eine solche Menge (Vgl: C total unzusammenhängend).
Kardinalität
Durch das 2. Cantorsche Diagonalverfahren lässt sich beweisen, dass die Cantor-Menge überabzählbar ist. Seien dazu [math] c_1, c_2, c_3 [/math] Elemente der Cantor-Menge.
Folgendes Bild veranschaulicht das Verfahren, an einem Beispiel.

Bild erstellt von Matilde Sciortino am 29.März 2021
Damit ist die Cantor-Menge gleichmächtig zum Intervall [0, 1] das ebenfalls, wie alle Intervalle, überabzählbar ist.
Musikalische Interpretation
Der rumänische Komponist György Ligeti macht in seiner Komposition "L'escalier du diable" (“Die Teufelstreppe”) innerhalb seiner 13. Etüde die Cantor-Funktion musikalisch fühlbar. [16] höre [19].
Der endliche Aufstieg des Intervalls [0, 1] in überabzählbar unendlich vielen Schritten ist durch sich selbstähnliche Harmonien illustriert. Die, aufgrund der herausgenommen Intervalle, konstanten Abschnitte der Cantorfunktion sind in Ligetis Werk erkennbar durch Tempi und Dynamik. Die steigende Monotonie der Funktion wird durch ein sich beschleunigendes Tempo in der Komposition ausgedrückt. Ihre Struktur ist analog zur Cantor-Menge dreiteilig. Nach dem ersten musikalischen Intervall wird der mittlere Teil des nächsten Intervall verändert und dann nochmals mit einem veränderten mittleren geteilt.
Die Komposition versucht eine Darstellung der unvorstellbaren Unendlichkeit in der Kunst zu geben, was in der Mathematik formal möglich ist.
Erdbeben und die Cantorfunktion
Der Seismologe Yuan Chen und seine Kollegen an der University of Missouri in Columbia haben in einer Studie herausgefunden, dass viele Starkbeben dem zeitlichen Muster der Cantorfunktion folgen. [17]
Die Forscher haben die zeitliche Abfolge von Starkbeben in Erdbebenzonen an der Plattengrenze zwischen Afrika und Eurasien im Westen Algeriens, im New-Madrid-Erdbebengebiet im Zentrum der USA und in Australien beobachtet.
„Es sind viele Erdbebensequenzen, die komplex und variabel sind [...] und zeigen Cluster von Ereignissen, die durch lange, aber unregelmäßige Intervalle der Ruhe unterbrochen sind“,[18] sagen Yuan Chen und sein Team.
Wenn man die Häufigkeitsverteilung der Beben in ein Diagramm einträgt, kann man an eine ansteigende Treppe mit verschiedenbreiten Stufen das Muster der Cantorfunktion, erkennen. Die Form der Treppe ist aber von der Region abhängig: Die Länge der Ruheintervalle, also die Breite der „Stufen“ ist mit der im Untergrund aufgestauten Spannung verbunden, je höher die Spannung, desto schmaler die Stufe.
Quellen und Bemerkungen
- ↑ Fröba, Wassermann: Die bedeutendsten Mathematiker, marix Verlag 2012, Abschnitt Georg Cantor
- ↑ Purkert, Walter & Ilgauds, Hans Joachim: Georg Cantor 1845–1918. 1987, S. 79 ff. und S.160.
- ↑ https://de.wikipedia.org/wiki/Georg_Cantor (zuletzt aufgerufen: 30.03.2021)
- ↑ Appell, Jürgen “Analysis in Beispielen und Gegenbeispielen. Eine Einführung in die Theorie reeller Funktionen”. Springer, Berlin u. a. 2009, ISBN 978-3-540-88902-1, S. 233–237
- ↑ Schilling, Anna (2021) : Cantor-Menge https://mampf.mathi.uni-heidelberg.de/mediaforward/medium/17786/manuscript/db62c69225719ba1d5495987b3d47991.pdf (letzter Zugriff 20.03.2021)
- ↑ Bildnachweis https://de.wikipedia.org/wiki/Cantor-Verteilung#/media/Datei:Cantor-Funktion.svg (letzter Zugriff 20.03.2021)
- ↑ Deiser, Oliver :Einführung in die Mengenlehre https://www.aleph1.info/?call=Puc&permalink=mengenlehre1_4_3 S.530-544 (letzter Zugriff 25.03.2021)
- ↑ Fleron, Julian F. “A Note on the History of the Cantor Set and Cantor Function.” Mathematics Magazine, vol. 67, no. 2, 1994, pp. 136–140. JSTOR, https://www.jstor.org/stable/2690689 (letzter Zugriff 18.03.2021)
- ↑ https://wiki.math.ntnu.no/_media/tma4225/2015h/cantor_set_function.pdf (letzter Zugriff 26.03.2021)
- ↑ Deiser, Oliver :Einführung in die Mengenlehre https://www.aleph1.info/?call=Puc&permalink=mengenlehre1_4_3 S.530-544 (letzter Zugriff 25.03.2021)
- ↑ Fleron, Julian F. “A Note on the History of the Cantor Set and Cantor Function.” Mathematics Magazine, vol. 67, no. 2, 1994, pp. 136–140. JSTOR, https://www.jstor.org/stable/2690689 (letzter Zugriff 18.03.2021)
- ↑ H. Amann, J. Escher: Analysis I
- ↑ Schilling, Anna (2021) : Cantor-Menge https://mampf.mathi.uni-heidelberg.de/mediaforward/medium/17786/manuscript/db62c69225719ba1d5495987b3d47991.pdf (letzter Zugriff 20.03.2021)
- ↑ https://mampf.mathi.uni-heidelberg.de/mediaforward/medium/17423/manuscript/b53706c913236535b9c57ba1da7e7eb4.pdf
- ↑ Wiegand, Kevin (2021): https://mampf.mathi.uni-heidelberg.de/mediaforward/medium/17423/manuscript/b53706c913236535b9c57ba1da7e7eb4.pdf (zuletzt aufgerufen: 30.03.2021)
- ↑ https://wiki.math.ntnu.no/_media/tma4225/2015h/cantor_set_function.pdf (letzter Zugriff 26.03.2021)
- ↑ https://pubs.geoscienceworld.org/ssa/bssa/article-abstract/110/3/1064/583503/Complex-Temporal-Patterns-of-Large-Earthquakes?redirectedFrom=fulltext (letzter Zugriff 30.03.2021)
- ↑ Podbregar, Nadja (2020):"Erdbeben folgen einer 'Teufelstreppe'": https://www.scinexx.de/news/geowissen/erdbeben-folgen-einer-teufelstreppe/ (zuletzt aufgerufen: 31.03.2021)
19. https://youtu.be/uoLam2O3gtY
Autoren
Christina Tian, Hannah Pompetzki, Matilde Sciortino, Marianna Hofmeier