Die Feigenbaum Konstante: Unterschied zwischen den Versionen

Aus FunFacts Wiki
Zur Navigation springen Zur Suche springen
K
 
(95 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt)
Zeile 1: Zeile 1:
−
δ%% ich glaube wir sollten das Thema noch umbenennen in "Logistische Gleichungen und die Feigenbaumkonstante" da das hier 80%logistische gleichung ist, die man braucht für die herleitung der feigenbaumkonstante und für den bezug zum mandelbrotset
+
[[Datei:LogisticMap BifurcationDiagram.png|alternativtext=Feigenbaum-Diagramm|mini|Das Feigenbaum-Diagramm<ref group="G">https://commons.wikimedia.org/wiki/File:LogisticMap_BifurcationDiagram.png</ref>]]Die Feigenbaum-Konstante  [math]\delta[/math] spielt in der Chaosforschung eine ähnlich große Rolle wie  <math>\pi</math> in der Geometrie oder  '''<math>\mathsf{e}</math>''' in der Analysis<ref>https://docplayer.org/18998902-Chaosforschung-fraktale-chaos-ordnung.html (Absatz 20, Zeile 8 ff. )</ref>. Sie bezeichnet den Wert gegen den das Verhältnis der Längen zwei aufeinander folgender Intervalle, die durch "Gabelungen" (Bifurkationen) begrenzt sind, konvergiert. (Siehe Graphik "Feigenbaum-Diagramm")
  
−
%-> find ich gut, aber ich weiß nicht wie man den Titel ändert.. Vlt müssen wir eine neue Seite erstellen.
+
Die Zahl wurde von [https://de.wikipedia.org/wiki/Mitchell_Feigenbaum Mitchell Feigenbaum] im Jahr 1975 entdeckt und ihr Zahlenwert wurde 1977 von den Physikern Siegfried Großmann und Stefan Thomae erstmals bestimmt.
−
 
 
−
%% HIER FRAGEN REINSCHREIBEN
 
−
 
 
−
== Die Feigenbaum-Konstante ==
 
−
[[Datei:LogisticMap BifurcationDiagram.png|alternativtext=Feigenbaum-Diagramm|mini|Das Feigenbaum-Diagramm]]
 
−
Die Feigenbaum-Konstante spielt in der Chaosforschung eine ähnlich große Rolle wie π in der Geometrie. Sie bezeichnet den Wert gegen den das Verhältnis der Längen zwei aufeinander folgender Intervalle, die durch "Gabeldungen" (Bifurkationen) begrenzt sind, konvergiert. (Siehe Graphik "Feigenbaum-Diagramm")
 
−
 
 
−
Die Zahl wurde von [https://de.wikipedia.org/wiki/Mitchell_Feigenbaum Mitchell Feigenbaum] im Jahr 1975 entdeckt und ihr Zahlenwert δ wurde 1977 von den Physikern Siegfried Großmann und Stefan Thomae erstmals bestimmt.
 
−
 
 
−
Es gilt: δ ≈ 4,6692
 
  
 +
Es gilt: <math>\delta\approx 4,6692</math>
 
== Die logistische Gleichung ==
 
== Die logistische Gleichung ==
−
Die logistische Gleichung wurde 1837 von [https://de.wikipedia.org/wiki/Pierre_Fran%C3%A7ois_Verhulst Pierre François Verhulst] eingeführt, um Populationen bzw. deren Entwicklung modellhaft darzustellen. Die Relevanz für die Feigenbaum-Konstante besteht darin, dass man den Wert an einer Stelle <math>r</math> im Feigenbaum-Diagramm auch als Grenzwert der Population mit dem entsprechenden Wachstumsfaktor interpretieren kann.
+
Die logistische Gleichung wurde 1837 von [https://de.wikipedia.org/wiki/Pierre_Fran%C3%A7ois_Verhulst Pierre François Verhulst] eingeführt, um Populationen bzw. deren Entwicklung modellhaft darzustellen.  
  
−
Sei <math>\boldsymbol{X}_n</math> die relative Größe einer Polulation zu einem Zeitpunkt <math>n</math> (zum Beispiel der Anteil der mit COVID-19 infizierten Menschen.) Man kann n als beliebiges Zeitntervall auffassen, so kann n beispielsweise Monate oder Jahre symbolisieren. <math>\boldsymbol{X}_0</math> bezeichnet die Startpolulation zum Zeitpunkt <math>n = 0</math>.
+
Sei <math>\boldsymbol{X}_n\in\lbrack 0,1\rbrack</math> die relative Größe einer Polulation (als Anteil an der maximal möglichen Population) zu einem Zeitpunkt <math>n</math> (zum Beispiel der Anteil der mit COVID-19 infizierten Menschen.) Man kann <math>n</math> als beliebiges Zeitintervall auffassen, so kann <math>n</math> beispielsweise Monate oder Jahre symbolisieren. <math>\boldsymbol{X}_0</math> bezeichnet die Startpolulation zum Zeitpunkt <math>n = 0</math>.
  
−
Dann berechnet sich die Population <math>\boldsymbol{X}_{n+1}</math> rekursiv mit der logistischen Gleichung:
+
Dann berechnet sich die Größe der Population <math>\boldsymbol{X}_{n+1}</math> rekursiv mit der logistischen Gleichung:
  
 
<math>\boldsymbol{X}_{n+1} = r*\boldsymbol{X}_n * (1-\boldsymbol{X}_n) </math>
 
<math>\boldsymbol{X}_{n+1} = r*\boldsymbol{X}_n * (1-\boldsymbol{X}_n) </math>
  
−
wobei der Parameter <math>r</math> der Wachstumsfaktor ist.  
+
wobei der Parameter <math>r\in\lbrack 0,4\rbrack</math>der Wachstumsfaktor ist.  
  
 
Die Gleichung berücksichtigt 2 Effekte:  
 
Die Gleichung berücksichtigt 2 Effekte:  
Zeile 28: Zeile 19:
 
1). Je größer die Population zum Zeitpunkt <math>n</math> ist, desto größer ist durch Vermehrung die nachfolgende Population.
 
1). Je größer die Population zum Zeitpunkt <math>n</math> ist, desto größer ist durch Vermehrung die nachfolgende Population.
  
−
2) Je näher die relative Größe der Population am Maximum (=1) ist, desto weniger Ressourcen (uninfizierte Menschen/Nahrung, ..) gibt es, sodass sich die Population wieder verringert.
+
2) Je näher die relative Größe der Population am Maximum (=1) ist, das durch natürliche Begrenzungen gegeben ist, desto weniger Ressourcen (uninfizierte Menschen/Nahrung, ..) gibt es, sodass sich die Population wieder verringert.
  
−
Das Verhalten der Folge hängt vom Wachstumsfaktor <math>r</math> ab.
+
=== Interpretation als Folge ===
 +
Dadurch, dass eine Population zum Zeitpunkt <math>n+1</math> durch die Population zum Zeitpunkt <math>n</math>berechnet wird, kann man <math>(\boldsymbol{X}_{n})_{n\in\mathbb{N}}</math> als rekursiv definierte Folge mit Startwert <math>\boldsymbol{X}_{0}</math> auffassen. Dabei muss <math>\boldsymbol{X}_{0}\in\lbrack 0,1\rbrack</math> gelten, denn trivialerweise muss die Population positiv sein und nicht größer als die obere Schranke.
  
−
=== Der Grentzwert der Folge ===
+
Das Verhalten der Folge hängt vom Wachstumsfaktor <math>r</math> ab. Dieser muss im Intervall [math][0,4][/math] liegen, denn falls [math]r<0[/math] ergeben sich negative Anteile an der Maximalpopulation und falls [math]r>4[/math] ergibt sich mit [math]\boldsymbol{X}_n = 0.5[/math] dass [math]\boldsymbol{X}_n+1 > 4*0.5*(1-0.5) = 1[/math] was größer als 100% der maximalen Population wäre.
−
Der Grenzwert der Folge wenn er existiert, ist unabhängig von dem Startwert <math>\boldsymbol{X}_0</math> und wird nur durch <math>r</math> bestimmt.  
 
  
−
Das ist leicht daran erkennbar, dass für <math>n \rightarrow \infty</math> gilt: <math>\boldsymbol{X}_{n+1} = \boldsymbol{X}_n</math> und somit mit <math>\boldsymbol{g}:=\frac{\lim}{n \rightarrow \infty } (\boldsymbol{X}_n)</math>
+
=== Der Grenzwert der Folge ===
 +
Der Grenzwert der Folge, wenn er existiert, ist unabhängig von dem Startwert <math>\boldsymbol{X}_0</math> und wird nur durch <math>r</math> bestimmt.
 +
 
 +
Das ist leicht daran erkennbar, dass mit <math>\boldsymbol{g}:=\lim\limits_{n \to \infty}\boldsymbol{X}_n</math>gilt, falls [math]g \neq 0[/math]:
  
 
<math>\boldsymbol{g} = r*\boldsymbol{g} * (1-\boldsymbol{g}) </math>
 
<math>\boldsymbol{g} = r*\boldsymbol{g} * (1-\boldsymbol{g}) </math>
Zeile 45: Zeile 39:
 
<math>\Rightarrow \boldsymbol{g}=\frac{(r-1)}{r}</math>
 
<math>\Rightarrow \boldsymbol{g}=\frac{(r-1)}{r}</math>
  
−
=== Beispiele: ===
+
Die Bedingung [math]g \neq 0[/math] ist nötig, um nicht durch 0 zu teilen. Im Abschnitt [[Die Feigenbaum Konstante#Verhalten in Abhängigkeit von r|Verhalten in Abhängigkeit von r]] wird gezeigt, dass das genau dann der Fall ist, wenn [math]r>1[/math].
−
Sei <math>\boldsymbol{X}_0 = 0,5</math> (also die Hälfte der maximal möglichen Population) und <math>r=2,5</math>.
 
  
−
Dann berechnet sich <math>\boldsymbol{X}_1 = 2,5*0,5*(1-0,5)=0,626 </math>, <math>\boldsymbol{X}_2 \approx 0,5859</math>, <math>\boldsymbol{X}_3 \approx 0,6065</math>, <math>\boldsymbol{X}_4 \approx 0,5966</math>, <math>\boldsymbol{X}_5 \approx 0,6017</math>, usw. Die Folge der <math>\boldsymbol{X}_n</math> nähert sich also dem Grenzwert <math>\frac{(2,5-1)}{2,5} = 0,6</math> alternierend, wie man auch gut in Graphik 1 sehen kann.
+
=== Beispiele ===
 +
Sei <math>\boldsymbol{X}_0 = 0.5</math> (also die Hälfte der maximal möglichen Population) und <math>r=2.5</math>.
  
−
Durch das selbe Beispiel mit Startwert <math>\boldsymbol{X}_0 = 0,1</math> sieht man, dass der Grenzwert unabhängig von der Startpopulation ist (Graphik 2).
+
Daraus ergibt sich:
 +
{| class="wikitable"
 +
|+
 +
!n
 +
![math]\boldsymbol{X}_n[/math]
 +
!n
 +
![math]\boldsymbol{X}_n[/math]
 +
|-
 +
|1
 +
|<math>2.5*0.5*(1-0.5)=0.626 </math>
 +
|36
 +
|[math]\approx 0.5999999999992 [/math]
 +
|-
 +
|2
 +
|<math>\approx 0.5859</math>
 +
|37
 +
|[math]\approx 0.6000000000004 [/math]
 +
|-
 +
|3
 +
|<math>\approx 0.6065</math>
 +
|38
 +
|[math]\approx 0.5999999999998 [/math]
 +
|-
 +
|4
 +
|<math>\approx 0.5966</math>
 +
|39
 +
|[math]\approx 0.6000000000001[/math]
 +
|-
 +
|5
 +
|<math>\approx 0.6017</math>
 +
|40
 +
|[math]\approx 0.6 [/math]
 +
|-
 +
|...
 +
|...
 +
|41
 +
|[math]\approx 0.6 [/math]
 +
|}
 +
Die Folge der <math>\boldsymbol{X}_n</math> nähert sich also dem Grenzwert <math>\frac{(2,5-1)}{2,5} = 0,6</math> alternierend, wie man auch gut in Graphik 1 sehen kann.
 +
 
 +
Bei demselben <math>r</math> mit Startwert <math>\boldsymbol{X}_0 = 0,1</math> sieht man, dass der Grenzwert unabhängig von der Startpopulation ist (Graphik 2).
 +
 
 +
Bei einem geringeren Wachstumsfaktor <math>r</math> ist auch der Grenzwert kleiner (Graphik 3).
  
 
<gallery widths="300" heights="200">
 
<gallery widths="300" heights="200">
−
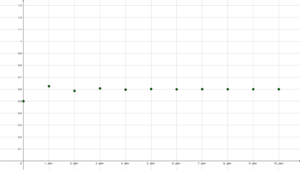
Datei:Population mit r=2,5.png|alt=Entwicklung einer Startpolulation X0=0,5 über 10 Jahre mit einem Wachstumsfaktor r=2,5|Graphik 1: Entwicklung einer Startpolulation X<sub>0</sub>=0,5 über 10 Jahre mit einem Wachstumsfaktor r=2,5
+
Datei:Population mit r=2,5.png|alt=Entwicklung einer Startpolulation X0=0,5 über 10 Jahre mit einem Wachstumsfaktor r=2,5|Graphik 1: Entwicklung einer Startpolulation X<sub>0</sub>=0.5 über 10 Jahre (dh. n [math]\le[/math] 10) mit einem Wachstumsfaktor r=2.5
−
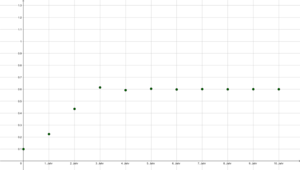
Datei:R=2,5, x0 = 0,1.png|alt=Entwicklung einer Startpolulation X0=0,1 über 10 Jahre mit einem Wachstumsfaktor r=2,5|Graphik 2: Entwicklung einer Startpolulation X<sub>0</sub>=0,1 über 10 Jahre mit einem Wachstumsfaktor r=2,5
+
Datei:R=2,5, x0 = 0,1.png|alt=Entwicklung einer Startpolulation X0=0,1 über 10 Jahre mit einem Wachstumsfaktor r=2,5|Graphik 2: Entwicklung einer Startpolulation X<sub>0</sub>=0.1 über 10 Jahre (dh. n [math]\le[/math] 10)mit einem Wachstumsfaktor r=2.5
 +
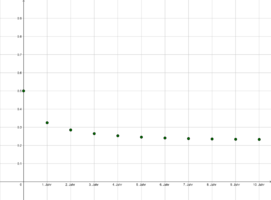
Datei:R=1,3.png|alt=Entwicklung einer Startpolulation X0=0,5 über 10 Jahre mit einem Wachstumsfaktor r=1,3|Graphik 3: Entwicklung einer Startpolulation X<sub>0</sub>=0.5 über 10 Jahre (dh. n [math]\le[/math] 10) mit einem Wachstumsfaktor r=1.3
 
</gallery>
 
</gallery>
  
 
== Verhalten in Abhängigkeit von r ==
 
== Verhalten in Abhängigkeit von r ==
−
[[Datei:Bifurkationsdiagramm.png|alternativtext=Entwicklung der Population in Abhängigkeit von r|mini|Diegramm 1: Entwicklung der Population in Abhängigkeit von r]]
+
[[Datei:Bifurkationsdiagramm.png|alternativtext=Entwicklung der Population in Abhängigkeit von r|mini|Diagramm 1: Entwicklung der Population in Abhängigkeit von r<ref group="G">http://rene.rondot.de/facharbeit/facharbeit-Title.html</ref>]]
−
Wenn auf der x-Achse der Wert von <math>r</math> aufgetragen wird und auf der y-Achse der entsprechende Grenzwert der Population, ergibt sich stückweise folgendes Diagramm 1:
+
Wenn auf der x-Achse der Wert von <math>r</math> aufgetragen wird und auf der y-Achse der entsprechende Grenzwert der Population, ergibt sich stückweise folgendes Diagramm 1<ref>https://www.j-berkemeier.de/LogistischeAbbildung.html</ref><ref>https://de.wikipedia.org/wiki/Logistische_Gleichung</ref>:
  
−
(#außerdem sollt ihr das Diagramm 1 bearbeiten, fügt farbige Boxen ein und schreibt die römischen zahlen rein, wie sie hier definiert sind von den Längen auf der XAchse)
+
=== '''Fall''' <math>\boldsymbol{I}: 0 \le r \le 1</math> ===
−
 
+
<blockquote>
−
'''Fall''' <math>\boldsymbol{I}: 0 \le r \le 1</math><blockquote>
 
 
Die Folge konvergiert gegen 0, d.h. die zu simulierende Populationen würden bei längerer Laufzeit aussterben.
 
Die Folge konvergiert gegen 0, d.h. die zu simulierende Populationen würden bei längerer Laufzeit aussterben.
−
</blockquote>'''Fall''' <math>\boldsymbol{II}:  1 < r \le 3</math><blockquote>
 
−
Die Folge/Population konvergiert gegen den Grenzwert <math>\frac{(r-1)}{r}</math>.
 
−
</blockquote>'''Fall''' <math>\boldsymbol{III}: 3 < r \le 1+\sqrt{6} \sim(3.45)</math><blockquote>
 
−
Die Folge/Population springt zwischen 2 Häufungspunkten.
 
 
</blockquote>
 
</blockquote>
  
−
=== Beispiel ===
+
=== '''Fall''' <math>\boldsymbol{II}:  1 < r \le 3</math> ===
−
[[Datei:R=3,2.png|alternativtext=r = 3,2: Population mit 2 Häufungspunkten|mini|Graphik 3: r = 3.2,  Folge mit 2 Häufungspunkten]]
+
<blockquote>
−
<math>\boldsymbol{X}_0 = 0,5 </math> und <math>r = 3,2</math>. Die darauf basierende Folge hat die Häufungspunkte H<sub>1</sub>≈ 0,513 und H<sub>2</sub> ≈ 0.8 (siehe Graphik 3).
+
Die Folge/Population konvergiert gegen den Grenzwert <math>g=\frac{r-1}{r}</math>.
  
−
Intuitiv kann man sich das so vorstellen, dass eine Population die zu schnell wächst, bereits im 1. Jahr eine Größe erreicht, sodass nicht mehr genügend Ressourcen vorhanden sind. Infolgedessen schrumpft die Population im Folgejahr wieder. Durch ihr starkes Wachstum hat sie im 3. Jahr aber bereits wieder die Überbevölkerung. Auf diese Weise ist jene Population stets am oszilieren.
+
Je größer <math>r</math> ist, desto größer ist auch der Grenzwert.  
 +
</blockquote>
  
−
Das führt zu der Bifurkation (Gabelung) im Diagramm 1 bei <math>r = 3</math>.
+
=== '''Fall''' <math>\boldsymbol{III}: 3 < r \le 1+\sqrt{6} \sim(3.45)</math> ===
 +
<blockquote>
 +
Die Folge/Population springt zwischen 2 Häufungspunkten. Das führt zu der Bifurkation (Gabelung) im Diagramm 1 bei <math>r = 3</math>.
  
−
Der größere der beiden Häufungspunkte ist mit wachsendem <math>r</math>  streng monoton steigend, der kleinere Häufungspunkt ist streng monoton fallend
+
Der größere der beiden Häufungspunkte ist mit wachsendem <math>r</math>  streng monoton steigend, der kleinere Häufungspunkt ist streng monoton fallend.
 +
</blockquote>
  
−
'''Fall''' <math>\boldsymbol{IV}: 1+\sqrt{6} \sim(3.45) \le r < 3,57 </math>
+
==== Beispiel ====
 +
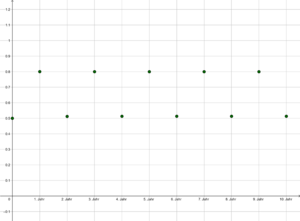
[[Datei:R=3,2.png|alternativtext=r = 3,2: Population mit 2 Häufungspunkten|mini|Graphik 4: r = 3.2,  Folge mit 2 Häufungspunkten]]
 +
<math>\boldsymbol{X}_0 = 0,5 </math> und <math>r = 3,2</math>. Die darauf basierende Folge hat die Häufungspunkte H<sub>1</sub>≈ 0,513 und H<sub>2</sub> ≈ 0.8 (siehe Graphik 4).
  
−
Bei ca. 3.45 fängt die zweite Bifurkation an und es gibt nun 4 Häufungspunkte
+
Intuitiv kann man sich das so vorstellen, dass eine Population die zu schnell wächst, bereits im 1. Jahr eine Größe erreicht, sodass nicht mehr genügend Ressourcen vorhanden sind. Dadruch schrumpft die Population im Folgejahr wieder. Durch ihr starkes Wachstum hat sie im 3. Jahr aber bereits wieder die Überbevölkerung erreicht. Auf diese Weise ist jene Population stets am oszilieren.
  
−
Die Anzahl der Häufungspunkte der Folge/Population verdoppelt sich mit steigendem <math>r</math> immer schneller, die nächste Verdopplung beginnt bei 3.54 . Ein Intervall, das durch 2 Bifurkationen begrenzt ist, wird dadurch immer kleiner. <blockquote>
+
=== '''Fall''' <math>\boldsymbol{IV}: (3.45)\sim 1+\sqrt{6}  < r < 3,57 </math> ===
−
Das Verhältnis der Längen zwei aufeinander folgender Intervalle konvergiert genau gegen die Feigenbaumkonstante δ ≈ 4,6692.
+
Bei ca. 3.45 fängt die zweite Bifurkation an und es gibt nun 4 Häufungspunkte.
−
</blockquote>'''Fall''' <math>\boldsymbol{V}: 3,57 \le r < 4</math>
 
  
−
nachdem sich die Anzahl der Häufungspunkte mit steigendem <math>r</math> bis zu 3.57 immer schneller verdoppelt fängt ab 3.57 plötzlich Chaos an. Die Folgen konvergieren nicht mehr gegen eine endlich Anzahl an Häufungspunkten, sondern bleiben chaotisch. Bei diesen chaotischen Parametern spielt auch der Anfangswert wieder eine Rolle, da er nun maßgeblich die Folge bestimmt.  
+
Die nächste Verdopplung beginnt bei 3.54, dort gibt es dann 8 Häufungspunkte. Die Anzahl der Häufungspunkte der Folge/Population verdoppelt sich mit steigendem <math>r</math> immer schneller.  Ein Intervall, das durch 2 Bifurkationen begrenzt ist, wird dadurch immer kleiner.
 +
=== '''Fall''' <math>\boldsymbol{V}: 3,57 \le r < 4</math> ===
 +
Nachdem sich die Anzahl der Häufungspunkte mit steigendem <math>r</math> bis zu 3.57 immer schneller verdoppelt, fängt ab ca. 3.57 plötzlich Chaos an. Dies bedeutet ,dass die Folgen nicht mehr gegen eine endliche Anzahl an Häufungspunkten konvergieren, sondern sich ohne erkennbare Muster fortsetzen. Bei diesen chaotischen Parametern spielt auch der Anfangswert wieder eine Rolle, da schon eine minimale Änderung eine ganz andere Folge erzeugt.  
  
−
Es existieren jedoch auch in diesem Bereich nicht chaotische Parameter. In der Umgebung von 3.82 gibt es ein Intervall mit 3 Häufungspunkten, welches in ein kleineres Intervall mit 6 Häufungspunkten übergeht usw. , bis es wieder in Chaos übergeht. Tatsächlich kann man für jede beliebige Anzahl von Häufungspunkten in diesem Bereich ein Intervall finden.
+
Es existieren jedoch auch in diesem Bereich nicht-chaotische Parameter. In der Umgebung von 3.82 gibt es ein Intervall mit 3 Häufungspunkten (der senkrechte weiße Streifen im hinteren Teil des Diagramms), welches in ein kleineres Intervall mit 6 Häufungspunkten übergeht usw. , bis es wieder in Chaos übergeht. Tatsächlich kann man für jede beliebige Anzahl von Häufungspunkten in diesem Bereich ein Intervall finden.
  
 
Schlussendlich liegen die nicht chaotischen Parameter dicht in diesem Bereich, d.h. in jedem noch so kleinen Teilintervall aus diesem Bereich befinden sich Parameter, mit denen die Folge gegen eine endliche Anzahl an Häufungspunkten konvergiert
 
Schlussendlich liegen die nicht chaotischen Parameter dicht in diesem Bereich, d.h. in jedem noch so kleinen Teilintervall aus diesem Bereich befinden sich Parameter, mit denen die Folge gegen eine endliche Anzahl an Häufungspunkten konvergiert
  
−
'''Fall''' <math>\boldsymbol{VI}: 4 ≤ r</math>
+
=== '''Fall''' <math>\boldsymbol{VI}: 4 ≤ r</math> ===
−
 
 
 
Die Folge wächst monoton und überschreitet somit auch bei einem groß gewählten <math>n</math> irgendwann die obere Populationsgrenze, und ist damit für Bevölkerungssimulationen nicht zu gebrauchen. Schlussendlich divergiert sie gegen <math>+ \infty</math>
 
Die Folge wächst monoton und überschreitet somit auch bei einem groß gewählten <math>n</math> irgendwann die obere Populationsgrenze, und ist damit für Bevölkerungssimulationen nicht zu gebrauchen. Schlussendlich divergiert sie gegen <math>+ \infty</math>
  
 
== Die Berechnung der Feigenbaumkonstante ==
 
== Die Berechnung der Feigenbaumkonstante ==
−
Ein Intervall ist ein Bifurkationsintervall, wenn für jedes r aus dem Intervall die Folge [math]\boldsymbol{X}_0[/math] die gleiche Anzahl an Häufungspunkten besitzt
+
Ein Intervall ist ein Bifurkationsintervall, wenn für jedes <math>r</math><nowiki> aus dem Intervall die Folge [math](\boldsymbol{X}_{n})_{n\in\mathbb{N}}[/math] die gleiche Anzahl an Häufungspunkten besitzt</nowiki>
−
 
 
−
Beispielsweise ist [3,3.45] ein Bifurkationsintervall, da jede die Folge [math]\boldsymbol{X}_0[/math] für jedes r aus diesem Intervall 2 Häufungspunkte hat (vgl [math]\boldsymbol{III}[/math]), dies nennen wir [math]\boldsymbol{A}_1[/math] und jedes drauffolgende [math]\boldsymbol{A}_n[/math] ist das zugehörige Intervall der Strecke mit 2^n Häufungspunkten. Diese dabei entstande Folge ist eine monoton fallende Nullfolge, ihre Reihe konvergiert gegen einen Wert ≈ 0.57, dies ist die Länge des in [math]\boldsymbol{III}[/math] und [math]\boldsymbol{IV}[/math] beschriebenen Bereichs.
 
−
 
 
−
Teilen wir die Länge zweier beliebiger benachbarter [math]\boldsymbol{A}_n[/math] dann kommt die schon oben erwähnte Feigenbaumkonstante raus.
 
  
−
%hier Bild einfügen der das Graphisch zeigt, am besten noch an zwei Stellen %Beispiel lässt sich hier gut durchrechnen mit A_2 und A_1 und A3 zu A2
+
Beispielsweise ist <math>\lbrack 3, 3.45\rbrack</math><nowiki> ein Bifurkationsintervall, da die Folge [math](\boldsymbol{X}_{n})_{n\in\mathbb{N}}[/math] für jedes </nowiki><math>r</math> aus diesem Intervall 2 Häufungspunkte hat (vgl [math]\boldsymbol{III}[/math]), dieses Intervall nennen wir [math]\boldsymbol{A}_1[/math] und jedes drauffolgende [math]\boldsymbol{A}_n[/math] ist das zugehörige Intervall mit <math>2^n</math> Häufungspunkten. Mit [math]|\boldsymbol{A}_n|[/math]bezeichnen wir die Länge des Intervalls [math]\boldsymbol{A}_n[/math]. Diese neu konstruierte Folge ist eine monoton fallende Nullfolge, deren Partialsumme konvergiert, d.h. [math]\sum_{n=1}^\infty|\boldsymbol{A}_n| \approx 0.57[/math], dies ist die Länge des in [math]\boldsymbol{III}[/math] und [math]\boldsymbol{IV}[/math] beschriebenen Bereichs.
  
−
A_n/A_(n+1)= δ  ≈ 4,6692 (#TEXEN)
+
Wir definieren nun die Folge [math]\boldsymbol{B}_n = \frac{| \boldsymbol{A}_{n}|}{|\boldsymbol{A}_{n+1}|}[/math], diese stellt die Verhältnisse zweier benachbarter Bifurkationsintervalle dar. Die Folge [math]\boldsymbol{B}_n[/math] konvergiert gegen die Feigenbaumkonstante  <math>\delta\approx 4,6692</math>. Diese Konstante ist nicht auf die logistische Gleichung beschränkt, sondern lässt sich beispielsweise mit der gleichen Methodik mit der Funktion <math>\boldsymbol{X}_{n+1}=\lambda*\sin(\boldsymbol{X}_n)</math>bestimmen.
  
−
Es ist tatsächlich egal ob wir das Verhältnis von A1 zu A2 betrachten oder von A1000 zu A1001, am Ende ergibt sich dabei immer die Feigenbaumkonstante. Sie ist auch nicht auf die logistische Gleichung beschränkt, sondern lässt sich beispielsweise auch errechnen in der Funktion  x_n+1= lambda*sin(x_N) (#texen  bild von dieser Funktion mit bsp. geogebra erstellen, danach die gleichen linien einfügen die in dem vorherigen Bild erstellt wurden)
+
{| class="wikitable"
 +
|+Berechnung von B<sub>n</sub>
 +
!n
 +
!A<sub>n</sub>
 +
!<nowiki>|A</nowiki><sub>n</sub><nowiki>|</nowiki>
 +
!B<sub>n</sub><nowiki>=|A</nowiki><sub>n</sub><nowiki>|/|A</nowiki><sub>n+1</sub><nowiki>|</nowiki>
 +
|-
 +
|1
 +
|[3,3.4494897]
 +
|0.4494897
 +
|4.7514
 +
|-
 +
|2
 +
|[3.4494897, 3.5440903]
 +
|0.0946006
 +
|4.6562
 +
|-
 +
|3
 +
|[3.5440903, 3.5644073]
 +
|0.020317
 +
|4.6683
 +
|-
 +
|4
 +
|[3.5644073, 3.5687594]
 +
|0.0043521
 +
|4.6686
 +
|-
 +
|5
 +
|[3.5687594, 3.5696916]
 +
|0.0009322
 +
|
 +
|}
  
−
== Bezug zum [[Mandelbrotmenge|Mandelbrotset]] ==
+
== Bezug zur [[Mandelbrotmenge|Mandelbrot-Menge]]<ref>https://de.wikipedia.org/wiki/Mandelbrot-Menge#Bezug_zur_Chaostheorie</ref> ==
 
<gallery widths="200" heights="200">
 
<gallery widths="200" heights="200">
−
Datei:Verhulst-Mandelbrot-Bifurcation.jpeg|Vergleich zum Mandelbrotset
+
Datei:Verhulst-Mandelbrot-Bifurcation.jpeg|Vergleich zum Mandelbrotset<ref group="G">https://de.wikipedia.org/wiki/Datei:Verhulst-Mandelbrot-Bifurcation.jpg</ref>
−
Datei:Mandelbrot Set – Periodicities coloured.png|Farbcodiertes Mandelbrotset
+
Datei:Mandelbrot Set – Periodicities coloured.png|Farbcodiertes Mandelbrotset, die Zahlen entsprechen der Anzahl an Häufungspunkten des jeweiligen Kardioiden<ref group="G">https://de.wikipedia.org/wiki/Datei:Mandelbrot_Set_%E2%80%93_Periodicities_coloured.png</ref>
−
</gallery>Schaut man sich die einen beschränkte Bereiche der reellen Zahlen in der Mandelbrotmenge an, ist die Anzahl der Häufungspunkte in der Mandelbrotiteration und der logistischen Gleichung gleich.
+
</gallery>Wir schauen uns nun einen beschränkten Bereich der reellen Zahlen an. Setzen wir in der rekursiven Folge [math]\boldsymbol{I}[/math] [math]z_{n+1}=z^2_{n}+c[/math] für c eine reelle Zahl aus dem Intervall [-0.75;0.25] ein, dann konvergiert die Folge und die c ist somit Teil der Mandelbrot-Menge. wenn c eine Zahl zwischen -0.75 und ca. -1.25 ist, dann konvergiert die Folge gegen einen alternierenden Grenzzyklus zwischen zwei Häufungspunkten. Je weiter das c gegen -1.5 geht, desto schneller verdoppelt sich die Anzahl der Häufungspunkte, bis es schlieslich in Chaos übergeht. Man erkennt Parallelen zu der Entwicklung des Feigenbaum-Diagramms, und kann dieses durch leichte isomorphe Veränderungen (Spiegelung an der y-Achse und eine Verschiebung und Streckung in Richtung der x-Achse) so positionieren, dass die Anzahl und Verteilung der Häufungspunkte des Feigenbaum-Diagramms und der Häufungspunkte der oben besprochenen Folge gleichen (siehe [//funfacts.mathi.uni-heidelberg.de/images/6/6d/Verhulst-Mandelbrot-Bifurcation.jpeg Vergleich zum Mandelbrotset]).  
−
 
 
−
Dieser Wert gilt für den gesamten Kardioid, in welchem  die ursprungliche reelle Zahl enthalten war. Somit lassen sich die Anzahl der Häufungspunkte von Kardioiden berechnen, welche Teile der reellen Achse überdecken.
 
−
 
 
−
Die Feigenbaumkonstante ist also gleichzeitig auch das Längenverhältnis der Kardioiden des Mandelbrotsets. 
 
−
 
 
−
=== _______________________________________________________________________________________________________________ ===
 
−
 
 
−
=== NOCH UNERLEDIGTEs zeug ===
 
−
 
 
−
___________
 
−
 
 
−
für christian:        (alles auf part 1 bezogen)    %% ==> mit X_n haben wir eine Folge (Ana1), X_0 muss dabei zwischen [0,1] sein (populationsstart sollte trivialerweise positiv sein und unter der oberen Schranke der Populationsgröße sein)
 
−
 
 
−
%% G>0
 
−
 
 
−
%% lambda>0 und kleiner als 4
 
−
 
 
−
und bin mir bei deiner errechnung von r-1/r nicht sicher XD
 
−
 
 
−
______
 
−
 
 
−
ich würde die graphik eins und zwei und drei noch so modifizieren, sodass die punkte mit linien verbunden werden, dann sieht das viel besser aus. (die linien dürfen nicht die Punkte übertrumpfen, sonst sieht es aus wie eine stetige FUnktion, obwohl wir nur natürliche Zahlen einsetzen können.
 
−
 
 
−
% im veritasium video min 7 wird das gezeigt, hier gibts definitiv coole möglichkeiten gifs einzufügen,
 
−
 
 
−
% Part 5: andere bezüge (veritasium vid. min 11)
 
−
 
 
−
____________________________________________________________________________________________________________________________
 
−
 
 
−
=== schon erledigtes zeug ===
 
−
%PART 1 .BASICS der Funktion (logistische Gleichung) https://de.wikipedia.org/wiki/Logistische_Gleichung
 
−
 
 
−
%% beispiel für lambda (fest gewählt) benutzen und zeigen dass für vchiedene Startwerte die Konvergenz für n gegen unendlich sich  nicht verändert und gegen den gleichen fixpunkt konvergiert, hier kann man zwei verschiedene X_0 benutzen und mit einer beispielrechnung zeigen, dass sie nach 10/20 schritten fast die gleichen ergebnisse haben
 
−
 
 
−
die hasen sketche sind ne schnapsidee, die man hätte machen können wenn mehr zeit wär, einfach ignorieren
 
−
 
 
−
%% beispiele anhand von Hasenpopulationen machen, Bilder mit kleinen niedlichen hasen einfügen, einer soll eine schrotflinte in der hand haben, und irgendwie den teil signalisieren , dass mehr hasen sterben als geboren werden wenn X_n                        n                                        ahe an 1 ist. die Folge X_n könnte dann z.b. die hasenpopulation darstellen in aufeinanderfolgenden Jahren
 
−
 
 
−
%%noch mehr Bilder mit süßen niedlichen hasen zeichnen
 
−
 
 
−
%PART 2: Der chaotische Graph https://upload.wikimedia.org/wikipedia/commons/7/7d/LogisticMap_BifurcationDiagram.png
 
−
 
 
−
%Wir bersprechen hier einen Graphen , dessen X Achse der lambda wert ist, und dessen y achse die häufungspunkte der Folge X_n mit diesem Lambda .
 
−
 
 
−
%(hier soll von links nach rechts der Graph immer ein bisschen mehr enthüllt werden)
 
−
 
 
−
%1.Teil : Tod ( 0=<lambda<= 1)
 
−
 
 
−
%DIe hasen population stirbt in jedem Fall aus, d.h. Die Fixpunkte sind null und somit auch Y-Wert
 
−
 
 
−
%Bild von Hasenfriedhof einzeichnen,soll aber trotzdem cute sein
 
−
 
 
−
%2.Teil : 1 Fixpunkt ( 1=<lambda<= 3)
 
−
 
 
−
%hier nähert sich die Population einem Fixpunkt an, man merkt auch dass es streng monoton wachsend ist
 
−
 
 
−
%3.Teil : 2 Fixpunkte(3<= lambda <= 1+Wurzel(6)) (ca.3.45))
 
−
 
 
−
%Die reihe konvergiert nicht mehr sondern hüpft zwischen zwei fixpunkten hin und her, der größere fixpunkt steigt monoton bei steigendem lambda, der kleiner fällt monoton
 
−
 
 
−
%4.Teil  2^n Fixpunkte (1+Wurzel(6)) (ca.3.45)<=  lambda <= ca.3,57)
 
−
 
 
−
%die anzahl der fixpunkte verdoppeln sich immer häufiger.
 
−
 
 
−
%5.Teil Chaos (3.57 <=lambda <= 4)
 
−
 
 
−
%joa chaos halt, hier ist auch plötzliche die Änderung des Startwertes doch wieder von Interesse, da durch minimale Änderungen der Startwerte sich alles ändern kann. Es gibt jedoch ab und zu mal werte, welche sich wieder stabilisieren, sieht man gut im Graphen
 
−
 
 
−
%#Bild von hasen zeichnen , der aus der Wirklichkeit rausglitcht
 
−
 
 
−
%6.Teil Divergenz lambda >4
 
−
 
 
−
%hier divergiert die folge ins unendliche
 
−
 
 
−
% Part3: DIE KONSTANTE: hierzu betrachten wir den 3 und 4. Teil des Graphen. Def. Bifurkationsintervall: Intervall von lambda welche die gleiche anzahl häufungspunkte haben. zb. [3,3.45] hat zwei Häufuingspunkte, dies nennen wir jetzt mal A_1 und jedes drauffolgende A_n ist das zugehörige Intervall der Strecke mit 2^n Häufungspunkten.
 
−
 
 
−
%Teilen wir die Länge zweier beliebiger benachbarter A_n dann kommt die Feigenbaumkonstante raus.  
 
−
 
 
−
%hier Bild einfügen der das Graphisch zeigt, am besten noch an zwei Stellen
 
  
−
%FBK = A_n/A_n+1
+
Wir betrachten nun die [https://de.wikipedia.org/wiki/Kardioide Kardioiden] der Mandelbrot-Menge anschauen  ,d.h. "Körper des Apfelmännchens" (siehe [//funfacts.mathi.uni-heidelberg.de/images/0/0e/Mandelbrot_Set_%E2%80%93_Periodicities_coloured.png Farbcodiertes Mandelbrotset]). Alle Werte, die das Innere eines Kardioiden bilden, besitzen die gleiche Anzahl an Häufungspunkten in der Folge [math]\boldsymbol{I}[/math]. Deshalb können wir durch die Bifurkationstheorie die Anzahl der Häufungspunkte von Kardioiden berechnen, welche Teile der beschränkten reellen Achse überdecken.
  
−
%Beispiel lässt sich hier gut durchrechnen mit A_2 und A_1
+
Auch hier konvergieren die Längenverhältnisse zweier Kardioiden der Mandelbrot-Menge gegen die Feigenbaumkonstante.
  
−
%nun lässt sich auch ausrechnen wann das Chaos beginnt, da wir mit A_n eine folge haben, welche immer kleiner wird (nullfolge) aka irgendwann die Verdopplung immer öfter passieren bis es dann zum chaos wird
+
== Quellen und Einzelnachweise ==
  
−
% es lassen sich auch andere funktionen benutzen, dort wird die Feigenbaumkonstante auch wieder vorkommen als Verhältnis der Bifurkationsintervalle (hier müssen wir noch herausfinden, bei welchen Funktionen das zutrifft, im video ist als anderes Beispiel x_n+1= lambda*sin(x_N)
+
=== Einzelnachweise ===
 +
<references />
  
−
% PaRT4:bezug zum mandelbrotset,
+
=== Grafiken ===
 +
<references group="G" />
  
−
%wenn man an bestimmten stellen ranzoomt, sieht der graph aus wie ein Fraktal
+
== Autoren ==
 +
Timo Ege
  
−
%hier wird definitiv ein querverweis auf das mandelbrotthema gemacht der anderen gruppe
+
Aaron Mäkel
  
−
%wenn man reelle zahlen einsetzt in die "mandelbrotfunktion" dann haben diese die gleiche anzahl an häufungspunkten wie die logistische funktion
+
Till Meldau
  
−
sollten wir quellen brauchen, dann ist hier noch: https://de.wikipedia.org/wiki/Mandelbrot-Menge#Bezug_zur_Chaostheorie
+
Christian Schön-Schöffel

Aktuelle Version vom 29. April 2021, 12:07 Uhr

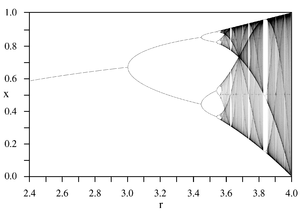
Feigenbaum-Diagramm
Das Feigenbaum-Diagramm[G 1]

Die Feigenbaum-Konstante [math]\delta[/math] spielt in der Chaosforschung eine ähnlich große Rolle wie  [math]\pi[/math] in der Geometrie oder  [math]\mathsf{e}[/math] in der Analysis[1]. Sie bezeichnet den Wert gegen den das Verhältnis der Längen zwei aufeinander folgender Intervalle, die durch "Gabelungen" (Bifurkationen) begrenzt sind, konvergiert. (Siehe Graphik "Feigenbaum-Diagramm")

Die Zahl wurde von Mitchell Feigenbaum im Jahr 1975 entdeckt und ihr Zahlenwert wurde 1977 von den Physikern Siegfried Großmann und Stefan Thomae erstmals bestimmt.

Es gilt: [math]\delta\approx 4,6692[/math]

Die logistische Gleichung

Die logistische Gleichung wurde 1837 von Pierre François Verhulst eingeführt, um Populationen bzw. deren Entwicklung modellhaft darzustellen.

Sei [math]\boldsymbol{X}_n\in\lbrack 0,1\rbrack[/math] die relative Größe einer Polulation (als Anteil an der maximal möglichen Population) zu einem Zeitpunkt [math]n[/math] (zum Beispiel der Anteil der mit COVID-19 infizierten Menschen.) Man kann [math]n[/math] als beliebiges Zeitintervall auffassen, so kann [math]n[/math] beispielsweise Monate oder Jahre symbolisieren. [math]\boldsymbol{X}_0[/math] bezeichnet die Startpolulation zum Zeitpunkt [math]n = 0[/math].

Dann berechnet sich die Größe der Population [math]\boldsymbol{X}_{n+1}[/math] rekursiv mit der logistischen Gleichung:

[math]\boldsymbol{X}_{n+1} = r*\boldsymbol{X}_n * (1-\boldsymbol{X}_n) [/math]

wobei der Parameter [math]r\in\lbrack 0,4\rbrack[/math]der Wachstumsfaktor ist.

Die Gleichung berücksichtigt 2 Effekte:

1). Je größer die Population zum Zeitpunkt [math]n[/math] ist, desto größer ist durch Vermehrung die nachfolgende Population.

2) Je näher die relative Größe der Population am Maximum (=1) ist, das durch natürliche Begrenzungen gegeben ist, desto weniger Ressourcen (uninfizierte Menschen/Nahrung, ..) gibt es, sodass sich die Population wieder verringert.

Interpretation als Folge

Dadurch, dass eine Population zum Zeitpunkt [math]n+1[/math] durch die Population zum Zeitpunkt [math]n[/math]berechnet wird, kann man [math](\boldsymbol{X}_{n})_{n\in\mathbb{N}}[/math] als rekursiv definierte Folge mit Startwert [math]\boldsymbol{X}_{0}[/math] auffassen. Dabei muss [math]\boldsymbol{X}_{0}\in\lbrack 0,1\rbrack[/math] gelten, denn trivialerweise muss die Population positiv sein und nicht größer als die obere Schranke.

Das Verhalten der Folge hängt vom Wachstumsfaktor [math]r[/math] ab. Dieser muss im Intervall [math][0,4][/math] liegen, denn falls [math]r<0[/math] ergeben sich negative Anteile an der Maximalpopulation und falls [math]r>4[/math] ergibt sich mit [math]\boldsymbol{X}_n = 0.5[/math] dass [math]\boldsymbol{X}_n+1 > 4*0.5*(1-0.5) = 1[/math] was größer als 100% der maximalen Population wäre.

Der Grenzwert der Folge

Der Grenzwert der Folge, wenn er existiert, ist unabhängig von dem Startwert [math]\boldsymbol{X}_0[/math] und wird nur durch [math]r[/math] bestimmt.

Das ist leicht daran erkennbar, dass mit [math]\boldsymbol{g}:=\lim\limits_{n \to \infty}\boldsymbol{X}_n[/math]gilt, falls [math]g \neq 0[/math]:

[math]\boldsymbol{g} = r*\boldsymbol{g} * (1-\boldsymbol{g}) [/math]

[math]\Rightarrow 1=r-r*\boldsymbol{g}[/math]

[math]\Rightarrow r*\boldsymbol{g}=r-1[/math]

[math]\Rightarrow \boldsymbol{g}=\frac{(r-1)}{r}[/math]

Die Bedingung [math]g \neq 0[/math] ist nötig, um nicht durch 0 zu teilen. Im Abschnitt Verhalten in Abhängigkeit von r wird gezeigt, dass das genau dann der Fall ist, wenn [math]r>1[/math].

Beispiele

Sei [math]\boldsymbol{X}_0 = 0.5[/math] (also die Hälfte der maximal möglichen Population) und [math]r=2.5[/math].

Daraus ergibt sich:

n [math]\boldsymbol{X}_n[/math] n [math]\boldsymbol{X}_n[/math]
1 [math]2.5*0.5*(1-0.5)=0.626 [/math] 36 [math]\approx 0.5999999999992 [/math]
2 [math]\approx 0.5859[/math] 37 [math]\approx 0.6000000000004 [/math]
3 [math]\approx 0.6065[/math] 38 [math]\approx 0.5999999999998 [/math]
4 [math]\approx 0.5966[/math] 39 [math]\approx 0.6000000000001[/math]
5 [math]\approx 0.6017[/math] 40 [math]\approx 0.6 [/math]
... ... 41 [math]\approx 0.6 [/math]

Die Folge der [math]\boldsymbol{X}_n[/math] nähert sich also dem Grenzwert [math]\frac{(2,5-1)}{2,5} = 0,6[/math] alternierend, wie man auch gut in Graphik 1 sehen kann.

Bei demselben [math]r[/math] mit Startwert [math]\boldsymbol{X}_0 = 0,1[/math] sieht man, dass der Grenzwert unabhängig von der Startpopulation ist (Graphik 2).

Bei einem geringeren Wachstumsfaktor [math]r[/math] ist auch der Grenzwert kleiner (Graphik 3).

  • Entwicklung einer Startpolulation X0=0,5 über 10 Jahre mit einem Wachstumsfaktor r=2,5

    Graphik 1: Entwicklung einer Startpolulation X0=0.5 über 10 Jahre (dh. n [math]\le[/math] 10) mit einem Wachstumsfaktor r=2.5

  • Entwicklung einer Startpolulation X0=0,1 über 10 Jahre mit einem Wachstumsfaktor r=2,5

    Graphik 2: Entwicklung einer Startpolulation X0=0.1 über 10 Jahre (dh. n [math]\le[/math] 10)mit einem Wachstumsfaktor r=2.5

  • Entwicklung einer Startpolulation X0=0,5 über 10 Jahre mit einem Wachstumsfaktor r=1,3

    Graphik 3: Entwicklung einer Startpolulation X0=0.5 über 10 Jahre (dh. n [math]\le[/math] 10) mit einem Wachstumsfaktor r=1.3

Verhalten in Abhängigkeit von r

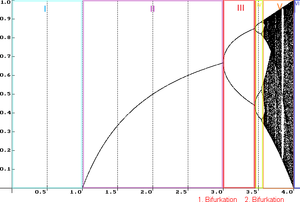
Entwicklung der Population in Abhängigkeit von r
Diagramm 1: Entwicklung der Population in Abhängigkeit von r[G 2]

Wenn auf der x-Achse der Wert von [math]r[/math] aufgetragen wird und auf der y-Achse der entsprechende Grenzwert der Population, ergibt sich stückweise folgendes Diagramm 1[2][3]:

Fall [math]\boldsymbol{I}: 0 \le r \le 1[/math]

Die Folge konvergiert gegen 0, d.h. die zu simulierende Populationen würden bei längerer Laufzeit aussterben.

Fall [math]\boldsymbol{II}: 1 \lt r \le 3[/math]

Die Folge/Population konvergiert gegen den Grenzwert [math]g=\frac{r-1}{r}[/math].

Je größer [math]r[/math] ist, desto größer ist auch der Grenzwert.

Fall [math]\boldsymbol{III}: 3 \lt r \le 1+\sqrt{6} \sim(3.45)[/math]

Die Folge/Population springt zwischen 2 Häufungspunkten. Das führt zu der Bifurkation (Gabelung) im Diagramm 1 bei [math]r = 3[/math].

Der größere der beiden Häufungspunkte ist mit wachsendem [math]r[/math] streng monoton steigend, der kleinere Häufungspunkt ist streng monoton fallend.

Beispiel

r = 3,2: Population mit 2 Häufungspunkten
Graphik 4: r = 3.2, Folge mit 2 Häufungspunkten

[math]\boldsymbol{X}_0 = 0,5 [/math] und [math]r = 3,2[/math]. Die darauf basierende Folge hat die Häufungspunkte H1≈ 0,513 und H2 ≈ 0.8 (siehe Graphik 4).

Intuitiv kann man sich das so vorstellen, dass eine Population die zu schnell wächst, bereits im 1. Jahr eine Größe erreicht, sodass nicht mehr genügend Ressourcen vorhanden sind. Dadruch schrumpft die Population im Folgejahr wieder. Durch ihr starkes Wachstum hat sie im 3. Jahr aber bereits wieder die Überbevölkerung erreicht. Auf diese Weise ist jene Population stets am oszilieren.

Fall [math]\boldsymbol{IV}: (3.45)\sim 1+\sqrt{6} \lt r \lt 3,57 [/math]

Bei ca. 3.45 fängt die zweite Bifurkation an und es gibt nun 4 Häufungspunkte.

Die nächste Verdopplung beginnt bei 3.54, dort gibt es dann 8 Häufungspunkte. Die Anzahl der Häufungspunkte der Folge/Population verdoppelt sich mit steigendem [math]r[/math] immer schneller. Ein Intervall, das durch 2 Bifurkationen begrenzt ist, wird dadurch immer kleiner.

Fall [math]\boldsymbol{V}: 3,57 \le r \lt 4[/math]

Nachdem sich die Anzahl der Häufungspunkte mit steigendem [math]r[/math] bis zu 3.57 immer schneller verdoppelt, fängt ab ca. 3.57 plötzlich Chaos an. Dies bedeutet ,dass die Folgen nicht mehr gegen eine endliche Anzahl an Häufungspunkten konvergieren, sondern sich ohne erkennbare Muster fortsetzen. Bei diesen chaotischen Parametern spielt auch der Anfangswert wieder eine Rolle, da schon eine minimale Änderung eine ganz andere Folge erzeugt.

Es existieren jedoch auch in diesem Bereich nicht-chaotische Parameter. In der Umgebung von 3.82 gibt es ein Intervall mit 3 Häufungspunkten (der senkrechte weiße Streifen im hinteren Teil des Diagramms), welches in ein kleineres Intervall mit 6 Häufungspunkten übergeht usw. , bis es wieder in Chaos übergeht. Tatsächlich kann man für jede beliebige Anzahl von Häufungspunkten in diesem Bereich ein Intervall finden.

Schlussendlich liegen die nicht chaotischen Parameter dicht in diesem Bereich, d.h. in jedem noch so kleinen Teilintervall aus diesem Bereich befinden sich Parameter, mit denen die Folge gegen eine endliche Anzahl an Häufungspunkten konvergiert

Fall [math]\boldsymbol{VI}: 4 ≤ r[/math]

Die Folge wächst monoton und überschreitet somit auch bei einem groß gewählten [math]n[/math] irgendwann die obere Populationsgrenze, und ist damit für Bevölkerungssimulationen nicht zu gebrauchen. Schlussendlich divergiert sie gegen [math]+ \infty[/math]

Die Berechnung der Feigenbaumkonstante

Ein Intervall ist ein Bifurkationsintervall, wenn für jedes [math]r[/math] aus dem Intervall die Folge [math](\boldsymbol{X}_{n})_{n\in\mathbb{N}}[/math] die gleiche Anzahl an Häufungspunkten besitzt

Beispielsweise ist [math]\lbrack 3, 3.45\rbrack[/math] ein Bifurkationsintervall, da die Folge [math](\boldsymbol{X}_{n})_{n\in\mathbb{N}}[/math] für jedes [math]r[/math] aus diesem Intervall 2 Häufungspunkte hat (vgl [math]\boldsymbol{III}[/math]), dieses Intervall nennen wir [math]\boldsymbol{A}_1[/math] und jedes drauffolgende [math]\boldsymbol{A}_n[/math] ist das zugehörige Intervall mit [math]2^n[/math] Häufungspunkten. Mit [math]|\boldsymbol{A}_n|[/math]bezeichnen wir die Länge des Intervalls [math]\boldsymbol{A}_n[/math]. Diese neu konstruierte Folge ist eine monoton fallende Nullfolge, deren Partialsumme konvergiert, d.h. [math]\sum_{n=1}^\infty|\boldsymbol{A}_n| \approx 0.57[/math], dies ist die Länge des in [math]\boldsymbol{III}[/math] und [math]\boldsymbol{IV}[/math] beschriebenen Bereichs.

Wir definieren nun die Folge [math]\boldsymbol{B}_n = \frac{| \boldsymbol{A}_{n}|}{|\boldsymbol{A}_{n+1}|}[/math], diese stellt die Verhältnisse zweier benachbarter Bifurkationsintervalle dar. Die Folge [math]\boldsymbol{B}_n[/math] konvergiert gegen die Feigenbaumkonstante [math]\delta\approx 4,6692[/math]. Diese Konstante ist nicht auf die logistische Gleichung beschränkt, sondern lässt sich beispielsweise mit der gleichen Methodik mit der Funktion [math]\boldsymbol{X}_{n+1}=\lambda*\sin(\boldsymbol{X}_n)[/math]bestimmen.

Berechnung von Bn
n An |An| Bn=|An|/|An+1|
1 [3,3.4494897] 0.4494897 4.7514
2 [3.4494897, 3.5440903] 0.0946006 4.6562
3 [3.5440903, 3.5644073] 0.020317 4.6683
4 [3.5644073, 3.5687594] 0.0043521 4.6686
5 [3.5687594, 3.5696916] 0.0009322

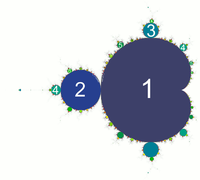
Bezug zur Mandelbrot-Menge[4]

  • Vergleich zum Mandelbrotset[G 3]

  • Farbcodiertes Mandelbrotset, die Zahlen entsprechen der Anzahl an Häufungspunkten des jeweiligen Kardioiden[G 4]

Wir schauen uns nun einen beschränkten Bereich der reellen Zahlen an. Setzen wir in der rekursiven Folge [math]\boldsymbol{I}[/math] [math]z_{n+1}=z^2_{n}+c[/math] für c eine reelle Zahl aus dem Intervall [-0.75;0.25] ein, dann konvergiert die Folge und die c ist somit Teil der Mandelbrot-Menge. wenn c eine Zahl zwischen -0.75 und ca. -1.25 ist, dann konvergiert die Folge gegen einen alternierenden Grenzzyklus zwischen zwei Häufungspunkten. Je weiter das c gegen -1.5 geht, desto schneller verdoppelt sich die Anzahl der Häufungspunkte, bis es schlieslich in Chaos übergeht. Man erkennt Parallelen zu der Entwicklung des Feigenbaum-Diagramms, und kann dieses durch leichte isomorphe Veränderungen (Spiegelung an der y-Achse und eine Verschiebung und Streckung in Richtung der x-Achse) so positionieren, dass die Anzahl und Verteilung der Häufungspunkte des Feigenbaum-Diagramms und der Häufungspunkte der oben besprochenen Folge gleichen (siehe Vergleich zum Mandelbrotset).

Wir betrachten nun die Kardioiden der Mandelbrot-Menge anschauen ,d.h. "Körper des Apfelmännchens" (siehe Farbcodiertes Mandelbrotset). Alle Werte, die das Innere eines Kardioiden bilden, besitzen die gleiche Anzahl an Häufungspunkten in der Folge [math]\boldsymbol{I}[/math]. Deshalb können wir durch die Bifurkationstheorie die Anzahl der Häufungspunkte von Kardioiden berechnen, welche Teile der beschränkten reellen Achse überdecken.

Auch hier konvergieren die Längenverhältnisse zweier Kardioiden der Mandelbrot-Menge gegen die Feigenbaumkonstante.

Quellen und Einzelnachweise

Einzelnachweise

  1. ↑ https://docplayer.org/18998902-Chaosforschung-fraktale-chaos-ordnung.html (Absatz 20, Zeile 8 ff. )
  2. ↑ https://www.j-berkemeier.de/LogistischeAbbildung.html
  3. ↑ https://de.wikipedia.org/wiki/Logistische_Gleichung
  4. ↑ https://de.wikipedia.org/wiki/Mandelbrot-Menge#Bezug_zur_Chaostheorie

Grafiken

  1. ↑ https://commons.wikimedia.org/wiki/File:LogisticMap_BifurcationDiagram.png
  2. ↑ http://rene.rondot.de/facharbeit/facharbeit-Title.html
  3. ↑ https://de.wikipedia.org/wiki/Datei:Verhulst-Mandelbrot-Bifurcation.jpg
  4. ↑ https://de.wikipedia.org/wiki/Datei:Mandelbrot_Set_%E2%80%93_Periodicities_coloured.png

Autoren

Timo Ege

Aaron Mäkel

Till Meldau

Christian Schön-Schöffel

Abgerufen von „https://funfacts.mathi.uni-heidelberg.de/index.php?title=Die_Feigenbaum_Konstante&oldid=4021“