Benutzer:Jan Agatz: Unterschied zwischen den Versionen
(Beweis-Container hinzugefügt.) |
(Bild hinzugefügt.) |
||
| (10 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 5: | Zeile 5: | ||
== Motivation == | == Motivation == | ||
Die Untersuchung von Gegenbeispielen lässt sich unter anderem durch folgende drei Punkte motivieren: | Die Untersuchung von Gegenbeispielen lässt sich unter anderem durch folgende drei Punkte motivieren: | ||
| − | * Gegenbeispiele können naheliegende und intuitiv richtige Aussage, die tatsächlich nicht gelten, widerlegen. So zeigt die Weierstraß-Funktion | + | * Gegenbeispiele können naheliegende und "intuitiv richtige" Aussage, die tatsächlich nicht gelten, widerlegen. So zeigt die [[Gegenbeispiele der Funktionentheorie und Analysis#Gegenbeispiele der Analysis#Weierstraß-Funktion|Weierstraß-Funktion]] , dass Stetigkeit auf einem Intervall nicht Differenzierbarkeit in (irgend-)einem Punkt implizieren muss. |
| − | * Weiter können diese beweisen, dass zwei Definitionen verschieden sind, und, je nach Situation, möglicherweise auch, wodrin diese Unterschiede liegen. So zeigt die Indikatorfunktion der rationalen Zahlen (in den reellen Zahlen), die Lebesgue-integrierbar, aber nicht Riemann-integrierbar ist, dass diese beiden Definition der Integrierbarkeit/des Integrals nicht zusammenfallen können. | + | * Weiter können diese beweisen, dass zwei Definitionen verschieden sind, und, je nach Situation, möglicherweise auch, wodrin diese Unterschiede liegen. So zeigt die [[Gegenbeispiele der Funktionentheorie und Analysis#Gegenbeispiele der Analysis#Die Indikatorfunktion der rationalen Zahlen|Indikatorfunktion der rationalen Zahlen (in den reellen Zahlen)]], die Lebesgue-integrierbar, aber nicht Riemann-integrierbar ist, dass diese beiden Definition der Integrierbarkeit/des Integrals nicht zusammenfallen können. |
* Schließlich zeigen Gegenbeispiele (einer bestimmten Aussage) meist pathologische Sonderfälle auf, die durch geschickte Wahl der Definition und Voraussetzung der Aussage ausgeschlossen werden können. | * Schließlich zeigen Gegenbeispiele (einer bestimmten Aussage) meist pathologische Sonderfälle auf, die durch geschickte Wahl der Definition und Voraussetzung der Aussage ausgeschlossen werden können. | ||
| Zeile 12: | Zeile 12: | ||
Neben der Funktionentheorie und der Topologie lassen sich auch in der Analysis viele Gegenbeispiele finden. | Neben der Funktionentheorie und der Topologie lassen sich auch in der Analysis viele Gegenbeispiele finden. | ||
| − | === Die Weierstraß-Funktion === | + | === Die Weierstraß-Funktion <ref>https://math.berkeley.edu/~brent/files/104_weierstrass.pdf</ref> === |
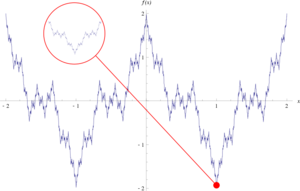
| + | [[Datei:Eine Weierstraß-Funktion.png|alternativtext=Bild eines Graphens einer Weierstraß-Funktion.|mini|Der Graph einer Weierstraß-Funktion, die überall stetig, aber nirgendwo differenzierbar ist.]] | ||
| + | Die '''Weierstraß-Funktion''' <math>f:\mathbb{R} \rightarrow \mathbb{R}</math> ist eine stetige Funktion, die in keinem Punkt differenzierbar ist. | ||
| − | + | Zur Definition wähle man [math]a \in (0,1)[/math] und [math]b \in \mathbb{N}[/math] ungerade, sodass <math>ab \gt 1 + \frac{3\pi}{2}</math>. Dann ist die Weierstraß-Funktion durch <math>f: \mathbb{R} \rightarrow \mathbb{R}, x \mapsto \sum\limits_{n = 0}^{\infty} a^n \cos\left(b^n \pi x\right)</math> gegeben. | |
| − | + | Man kann zeigen, dass | |
| − | |||
| − | |||
| − | |||
# die Weierstraß-Funktion <math>f</math> stetig ist. | # die Weierstraß-Funktion <math>f</math> stetig ist. | ||
# die Weierstraß-Funktion <math>f</math> in keinem Punkt differenzierbar ist. | # die Weierstraß-Funktion <math>f</math> in keinem Punkt differenzierbar ist. | ||
{| class="wikitable left mw-collapsible mw-collapsed font-size: 100%;" | {| class="wikitable left mw-collapsible mw-collapsed font-size: 100%;" | ||
| − | | style="text-align:left; font-size: 100%;" | '''Beweis | + | | style="text-align:left; font-size: 100%;" | '''Beweis der Stetigkeit''' |
|- | |- | ||
| Man betrachte die Weierstraß-Funktion als Funktionenreihe der Funktionen <math>\left(f_n: \mathbb{R} \rightarrow \mathbb{R}, x \mapsto a^n \cos\left(b^n\pi x\right)\right)_{n \in \mathbb{N}}</math>, die jeweils stetig in <math>x</math> sind und der Abschätzung <math>|a^n \cos\left(b^n\pi x\right)| \leq |a^n| \leq a^n</math> genügen. | | Man betrachte die Weierstraß-Funktion als Funktionenreihe der Funktionen <math>\left(f_n: \mathbb{R} \rightarrow \mathbb{R}, x \mapsto a^n \cos\left(b^n\pi x\right)\right)_{n \in \mathbb{N}}</math>, die jeweils stetig in <math>x</math> sind und der Abschätzung <math>|a^n \cos\left(b^n\pi x\right)| \leq |a^n| \leq a^n</math> genügen. | ||
| − | Als geometrische Reihe konvergiert <math>\sum\limits_{n = 0}^{\infty} a^n = \frac{1}{1 - a}</math>, | + | Als geometrische Reihe konvergiert <math>\sum\limits_{n = 0}^{\infty} a^n = \frac{1}{1 - a}</math>, sodass (über den [https://de.wikipedia.org/wiki/Weierstraßsches_Majorantenkriterium Majorantensatz von Weierstraß]) auch die Funktionenreihe <math>\sum\limits_{n = 0}^{\infty} a^n\cos\left(b^n\pi x\right)</math> gleichmäßig auf <math>\mathbb{R}</math> konvergiert. |
| − | Nimmt man beide obigen Aussagen zusammen, so folgt bereits, dass die Weierstraß-Funktion als gleichmäßig konvergente Funktionsreihe stetiger Funktionen selbst stetig ist. | + | Nimmt man beide obigen Aussagen zusammen, so folgt bereits, dass die Weierstraß-Funktion als gleichmäßig konvergente Funktionsreihe stetiger Funktionen selbst stetig ist. <ref>Winfried Kohnen: ''Analysis 1: Vorlesung von Prof. Dr. Kohnen'', Kapitel 5.4, Satz 4</ref> |
|} | |} | ||
{| class="wikitable left mw-collapsible mw-collapsed font-size: 100%;" | {| class="wikitable left mw-collapsible mw-collapsed font-size: 100%;" | ||
| − | | style="text-align:left; font-size: 100%;" | '''Beweis der | + | | style="text-align:left; font-size: 100%;" | '''Beweis der Nicht-Differenzierbarkeit''' |
|- | |- | ||
| − | | Sei nun <math>x_0 \in \mathbb{R}</math> ein beliebiger Punkt. Um zu zeigen, dass in diesem Punkt die Ableitung der Weierstraß-Funktion, also der Grenzwert <math>\lim\limits_{x \to x_0} \frac{f(x) - f(x_0)}{x - x_0}</math>, nicht existiert, reicht es eine Folge zu finden, die gegen <math>x_0</math> konvergiert, während der Differenzenquotient keinen Grenzwert in <math>\mathbb{R}</math> besitzt. | + | | Sei nun <math>x_0 \in \mathbb{R}</math> ein beliebiger Punkt. Um zu zeigen, dass in diesem Punkt die Ableitung der Weierstraß-Funktion, also der Grenzwert <math>\lim\limits_{x \to x_0} \frac{f(x) - f(x_0)}{x - x_0}</math>, nicht existiert, reicht es eine Folge zu finden, die gegen <math>x_0</math> konvergiert, während der dazugehörige Differenzenquotient keinen Grenzwert in <math>\mathbb{R}</math> besitzt. |
| + | |||
| + | Man wähle nun für jedes <math>m \in \mathbb{N}</math> die eindeutige ganze Zahl <math>c_m \in \mathbb{Z}</math>, sodass <math>b^m x_0 - c_m \in \left(-\frac{1}{2}, \frac{1}{2}\right]</math> gilt. Weiter definiere man für jedes <math>m \in \mathbb{N}</math> die reellen Zahlen <math>x_m := b^m x_0 - c_m</math> und <math>y_m := \frac{c_m - 1}{b^m}</math>. | ||
| − | + | Für diese gelten die Ungleichung <math>y_m - x_0 = - \frac{1 + x_m}{b^m} \lt 0 </math>, also <math>y_m \lt x_0</math>. Insbesondere folgt nun: | |
| + | * <math>\lim\limits_{m \to \infty} |y_m - x_0| = \lim\limits_{m \to \infty} x_0 - y_m = \lim\limits_{m \to \infty} \frac{1 + x_m}{b^m} = 0</math>. | ||
| − | <math>y_m | + | Die Folge <math>(y_m)_{m \in \mathbb{N}}</math> konvergiert also von unten gegen <math>x_0</math>. |
| − | |||
| − | |||
| − | + | Weiter gilt: | |
| − | + | ||
| + | <math>\phantom{=}\frac{f(y_m) - f(x_0)}{y_m - x_0} = \frac{\sum\limits_{n = 0}^{\infty}a^n\cos\left(b^n\pi y_m\right) - \sum\limits_{n = 0}^{\infty}a^n\cos\left(b^n\pi x_0\right)}{y_m - x_0} \\ | ||
= \sum\limits_{n = 0}^{\infty} a^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{y_m - x_0} \\ | = \sum\limits_{n = 0}^{\infty} a^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{y_m - x_0} \\ | ||
= \sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)} + \sum\limits_{n = m}^{\infty} a^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{y_m - x_0} \\ | = \sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)} + \sum\limits_{n = m}^{\infty} a^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{y_m - x_0} \\ | ||
= \sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)} + \sum\limits_{n = 0}^{\infty} a^{n + m} \frac{\cos\left(b^{n + m}\pi y_m\right) - \cos\left(b^{n + m}\pi x_0\right)}{y_m - x_0} | = \sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)} + \sum\limits_{n = 0}^{\infty} a^{n + m} \frac{\cos\left(b^{n + m}\pi y_m\right) - \cos\left(b^{n + m}\pi x_0\right)}{y_m - x_0} | ||
</math>. | </math>. | ||
| + | |||
Die erste Summe lässt sich nun mithilfe einer [https://de.wikipedia.org/wiki/Formelsammlung_Trigonometrie#Summen_zweier_trigonometrischer_Funktionen_(Identitäten) trigonometrischen Identität] umformen; dann gilt: | Die erste Summe lässt sich nun mithilfe einer [https://de.wikipedia.org/wiki/Formelsammlung_Trigonometrie#Summen_zweier_trigonometrischer_Funktionen_(Identitäten) trigonometrischen Identität] umformen; dann gilt: | ||
| − | <math>\sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)}\\ | + | |
| + | <math>\phantom{=}\sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)}\\ | ||
=\sum\limits_{n = 0}^{m - 1} \frac{-2(ab)^n }{b^n(y_m - x_0)}\sin\left(\frac{b^n\pi(y_m + x_0)}{2}\right)\sin\left(\frac{b^n\pi(y_m - x_0)}{2}\right) \\ | =\sum\limits_{n = 0}^{m - 1} \frac{-2(ab)^n }{b^n(y_m - x_0)}\sin\left(\frac{b^n\pi(y_m + x_0)}{2}\right)\sin\left(\frac{b^n\pi(y_m - x_0)}{2}\right) \\ | ||
= \sum\limits_{n = 0}^{m - 1}-\pi(ab)^n\sin\left(\frac{b^n\pi(y_m + x_0)}{2}\right)\frac{\sin\left(\frac{b^n\pi(y_m - x_0)}{2}\right)}{\frac{b^n\pi(y_m - x_0)}{2}} | = \sum\limits_{n = 0}^{m - 1}-\pi(ab)^n\sin\left(\frac{b^n\pi(y_m + x_0)}{2}\right)\frac{\sin\left(\frac{b^n\pi(y_m - x_0)}{2}\right)}{\frac{b^n\pi(y_m - x_0)}{2}} | ||
</math>. | </math>. | ||
| − | Verwendet man nun die Dreiecks-Ungleichung und den Fakt, dass <math>\left|\frac{\sin(x)}{x}\right | + | Verwendet man nun die Dreiecks-Ungleichung und den Fakt, dass <math>\left|\frac{\sin(x)}{x}\right| \leq 1</math> für alle <math>x \in \mathbb{R}\setminus\{0\}</math>, so ergibt sich weiter die Abschätzung: |
| − | <math>\left|\sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)}\right| | + | |
| + | <math>\phantom{=}\left|\sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)}\right| | ||
\leq \sum\limits_{n = 0}^{m - 1}\pi (ab)^n = \pi\frac{(ab)^m - 1}{ab - 1} \lt \pi \frac{(ab)^m}{ab - 1}</math>. | \leq \sum\limits_{n = 0}^{m - 1}\pi (ab)^n = \pi\frac{(ab)^m - 1}{ab - 1} \lt \pi \frac{(ab)^m}{ab - 1}</math>. | ||
Es existiert also ein <math>\epsilon \in (-1, 1)</math>, sodass <math>\sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)} = \epsilon \pi \frac{(ab)^m}{ab - 1}</math>. | Es existiert also ein <math>\epsilon \in (-1, 1)</math>, sodass <math>\sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)} = \epsilon \pi \frac{(ab)^m}{ab - 1}</math>. | ||
| + | |||
Für die Terme in der zweiten Summe lassen sich folgende Vereinfachungen finden, wenn man beachtet, dass <math>b</math> eine ungerade und <math>c_m</math> eine beliebige ganze Zahl ist: | Für die Terme in der zweiten Summe lassen sich folgende Vereinfachungen finden, wenn man beachtet, dass <math>b</math> eine ungerade und <math>c_m</math> eine beliebige ganze Zahl ist: | ||
* <math>\cos\left(b^{n + m}\pi y_m\right) = \cos\left(b^n\pi (c_m - 1)\right) = (-1)^{b^n (c_m - 1)} = (-1)^{c_m - 1} = -(-1)^{c_m}</math> | * <math>\cos\left(b^{n + m}\pi y_m\right) = \cos\left(b^n\pi (c_m - 1)\right) = (-1)^{b^n (c_m - 1)} = (-1)^{c_m - 1} = -(-1)^{c_m}</math> | ||
Und mit dem [https://de.wikipedia.org/wiki/Formelsammlung_Trigonometrie#Additionstheoreme trigonometrischen Additionstheorem für den Kosinus] erhält man: | Und mit dem [https://de.wikipedia.org/wiki/Formelsammlung_Trigonometrie#Additionstheoreme trigonometrischen Additionstheorem für den Kosinus] erhält man: | ||
| − | * <math>\cos\left(b^{n + m}\pi x_0\right) = \cos\left(b^n\pi(x_m + c_m)\right) = \cos\left(b^n\pi x_m\right)\cos\left(b^n \pi c_m\right) - \sin\left(b^n \pi x_m\right)\sin\left(b^n \pi c_m\right) | + | * <math>\cos\left(b^{n + m}\pi x_0\right) = \cos\left(b^n\pi(x_m + c_m)\right) = \cos\left(b^n\pi x_m\right)\cos\left(b^n \pi c_m\right) - \sin\left(b^n \pi x_m\right)\sin\left(b^n \pi c_m\right) = (-1)^{b^n c_m}\cos\left(b^n \pi c_m\right) - 0 = (-1)^{c_m}\cos\left(b^n\pi c_m\right)</math>. |
| − | Damit ergibt sich:<math>\sum\limits_{n = 0}^{\infty} a^{n + m} \frac{\cos\left(b^{n + m}\pi y_m\right) - \cos\left(b^{n + m}\pi x_0\right)}{y_m - x_0} \\ | + | |
| + | Damit ergibt sich: | ||
| + | |||
| + | <math>\phantom{=}\sum\limits_{n = 0}^{\infty} a^{n + m} \frac{\cos\left(b^{n + m}\pi y_m\right) - \cos\left(b^{n + m}\pi x_0\right)}{y_m - x_0} \\ | ||
= \sum\limits_{n = 0}^{\infty} a^{n + m} \frac{-(-1)^{c_m} - (-1)^{c_m}\cos\left(b^n\pi x_m\right)}{y_m - x_0} \\ | = \sum\limits_{n = 0}^{\infty} a^{n + m} \frac{-(-1)^{c_m} - (-1)^{c_m}\cos\left(b^n\pi x_m\right)}{y_m - x_0} \\ | ||
= \sum\limits_{n = 0}^{\infty} a^{n + m}(-1)(-1)^{c_m} \frac{1 + \cos\left(b^n\pi x_m\right)}{-\frac{1 + x_m}{b^n}} \\ | = \sum\limits_{n = 0}^{\infty} a^{n + m}(-1)(-1)^{c_m} \frac{1 + \cos\left(b^n\pi x_m\right)}{-\frac{1 + x_m}{b^n}} \\ | ||
| − | = (ab)^m(-1)^{c_m}\sum\limits_{n = 0}^{\infty} a^{n} \frac{1 + \cos\left(b^n\pi x_m\right)}{1 + x_m} | + | = (ab)^m(-1)^{c_m}\sum\limits_{n = 0}^{\infty} a^{n} \frac{1 + \cos\left(b^n\pi x_m\right)}{1 + x_m}. |
</math> | </math> | ||
| − | |||
| − | <math>\sum\limits_{n = 0}^{\infty} a^n \frac{1 + \cos\left(b^n\pi x_m\right)}{1 + x_m} \geq \frac{1 + \cos\left(\pi x_m\right)}{1 + x_m} \geq \frac{1}{1 + \frac{1}{2}} = \frac{2}{3}</math>, | + | Beachtet man, dass <math>x_m \in \left(-\frac{1}{2}, \frac{1}{2}\right]</math>, so folgt, dass alle Terme der obigen Summe positiv sind. Lässt man alle Terme für <math>n \geq 1</math> weg, so ergibt sich die Abschätzung: |
| + | |||
| + | <math>\phantom{=}\sum\limits_{n = 0}^{\infty} a^n \frac{1 + \cos\left(b^n\pi x_m\right)}{1 + x_m} \geq \frac{1 + \cos\left(\pi x_m\right)}{1 + x_m} \geq \frac{1}{1 + \frac{1}{2}} = \frac{2}{3}</math>, | ||
es gibt also ein <math>\eta \geq 1</math>, sodass <math>(ab)^m(-1)^{c_m}\sum\limits_{n = 0}^{\infty} a^{n} \frac{1 + \cos\left(b^n\pi x_m\right)}{1 + x_m} = \frac{2}{3}(ab)^m(-1)^{c_m}\eta</math>. | es gibt also ein <math>\eta \geq 1</math>, sodass <math>(ab)^m(-1)^{c_m}\sum\limits_{n = 0}^{\infty} a^{n} \frac{1 + \cos\left(b^n\pi x_m\right)}{1 + x_m} = \frac{2}{3}(ab)^m(-1)^{c_m}\eta</math>. | ||
| + | |||
Fügt man nun die Ausdrücke für beide Summen zusammen, so erhält man: | Fügt man nun die Ausdrücke für beide Summen zusammen, so erhält man: | ||
| − | <math>\frac{f(y_m) - f(x_0)}{y_m - x_0} = \sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)} + \sum\limits_{n = 0}^{\infty} a^{n + m} \frac{\cos\left(b^{n + m}\pi y_m\right) - \cos\left(b^{n + m}\pi x_0\right)}{y_m - x_0} = \epsilon\frac{\pi(ab)^m}{ab - 1} + \frac{2}{3}(ab)^m(-1)^{c_m}\eta = (-1)^{c_m}(ab)^m\eta\left(\frac{2}{3} + (-1)^{c_m}\frac{\epsilon}{\eta}\frac{\pi}{ab - 1}\right)</math>. | + | <math>\phantom{=}\frac{f(y_m) - f(x_0)}{y_m - x_0} = \sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)} + \sum\limits_{n = 0}^{\infty} a^{n + m} \frac{\cos\left(b^{n + m}\pi y_m\right) - \cos\left(b^{n + m}\pi x_0\right)}{y_m - x_0} = \epsilon\frac{\pi(ab)^m}{ab - 1} + \frac{2}{3}(ab)^m(-1)^{c_m}\eta = (-1)^{c_m}(ab)^m\eta\left(\frac{2}{3} + (-1)^{c_m}\frac{\epsilon}{\eta}\frac{\pi}{ab - 1}\right)</math>. |
| + | |||
| + | |||
| + | Erinnert man sich, dass <math>a</math> und <math>b</math> so gewählt wurden, dass <math>ab \gt 1 + \frac{3\pi}{2} \iff \frac{\pi}{ab - 1} = \frac{2}{3}</math> und weiter <math>|\epsilon| \lt 1 </math> und <math>\eta \geq 1</math> gelten, so ergibt sich: | ||
| − | + | <math>\phantom{=}\frac{2}{3} + (-1)^{c_m}\frac{\epsilon}{\eta}\frac{\pi}{ab - 1} \gt \frac{2}{3} - \frac{\pi}{ab - 1} \gt 0</math>. | |
| − | |||
Insbesondere folgt: | Insbesondere folgt: | ||
| − | <math>\left|\frac{f(y_m) - f(x_0)}{y_m - x_0}\right| \gt (ab)^m\left(\frac{2}{3} - \frac{\pi}{ab - 1}\right) \rightarrow \infty</math>, | + | <math>\phantom{=}\left|\frac{f(y_m) - f(x_0)}{y_m - x_0}\right| \gt (ab)^m\left(\frac{2}{3} - \frac{\pi}{ab - 1}\right) \rightarrow \infty</math>, |
sodass <math>f</math> nicht in <math>x_0</math> differenzierbar sein kann. Da <math>x_0</math> beliebig gewählt war, ist die Weierstraß-Funktion <math>f</math> also nirgendwo differenzierbar. | sodass <math>f</math> nicht in <math>x_0</math> differenzierbar sein kann. Da <math>x_0</math> beliebig gewählt war, ist die Weierstraß-Funktion <math>f</math> also nirgendwo differenzierbar. | ||
|} | |} | ||
| − | === Die modifizierte Dirichlet-Funktion === | + | === Die modifizierte Dirichlet-Funktion<ref>Jürgen Appell, op. cit., Beispiel 1.12</ref>=== |
| − | Eine weitere interessante Funktion, die das intuitive Verständnis der Stetigkeit herausfordert, ist die modifizierte Dirichlet-Funktion | + | [[Datei:Thomaesche Funktion.png|alternativtext=Bild des Graphens der modifizierten Dirichlet-Funktion auf dem Intervall (0,1).|mini|Graph der modifizierten Dirichlet-Funktion auf dem Intervall (0,1).]] |
| + | Eine weitere interessante Funktion, die das intuitive Verständnis der Stetigkeit herausfordert, ist die '''modifizierte Dirichlet-Funktion'''. Diese ist teilweise auch als '''thomaesche Funktion''' bekannt. | ||
| + | |||
| + | Diese ist definiert durch <math>g: \mathbb{R} \rightarrow \mathbb{R}, x \mapsto \begin{cases}\frac{1}{q} & \text{für } x = \frac{p}{q} \in \mathbb{Q} \\ 0 & \text{für } x \in \mathbb{R}\setminus\mathbb{Q} \end{cases}</math>, sodass die Funktion folgende sonderbaren Eigenschaften hat: | ||
| + | # Sie ist in den rationalen Zahlen <math>\mathbb{Q}</math> unstetig. | ||
| + | # Sie ist in den irrationalen Zahlen <math>\mathbb{R}\setminus\mathbb{Q}</math> stetig. | ||
{| class="wikitable left mw-collapsible mw-collapsed font-size: 100%;" | {| class="wikitable left mw-collapsible mw-collapsed font-size: 100%;" | ||
| − | | style="text-align:left; font-size: 100%;" | '''Beweis der Unstetigkeit''' | + | | style="text-align:left; font-size: 100%;" | '''Beweis der Unstetigkeit in den rationalen Zahlen''' |
|- | |- | ||
| − | | Wir zeigen zuerst die Unstetigkeit in den rationalen Zahlen | + | | Wir zeigen zuerst die Unstetigkeit in den rationalen Zahlen. |
| − | Sei nun <math>0 \lt \epsilon \leq \frac{1}{q}</math>. Es ist bekannt, dass für jedes <math>\delta \in \mathbb{R}_{\gt 0}</math> unendlich viele | + | Dafür sei <math>x \in \mathbb{Q}</math> eine beliebige rationale Zahl, sowie <math>p \in \mathbb{Z}, q \in \mathbb{N}</math> die (eindeutigen) teilerfremden ganzen Zahlen, sodass <math>x = \frac{p}{q}</math>. Damit gilt dann: <math>g(x_0) = \frac{1}{q}</math>. |
| + | |||
| + | Sei nun <math>0 \lt \epsilon \leq \frac{1}{q}</math>. Es ist bekannt, dass für jedes <math>\delta \in \mathbb{R}_{\gt 0}</math> unendlich viele irrationale Zahlen in der Umgebung <math>U_\delta (x_0) = (x_0 - \delta, x_0 + \delta)</math> liegen. Für eine beliebige irrationale Zahl <math>x \in U_\delta (x_0) \cap \mathbb{R}\setminus\mathbb{Q}</math> gilt nun: <math>|f(x_0) - f(x)| = |\frac{1}{q} - 0| = \frac{1}{q} \geq \varepsilon</math>. | ||
Da <math>\delta</math> beliebig gewählt war, kann <math>g</math> nicht stetig in <math>x_0</math> sein. Da <math>x_0</math> beliebig gewählt war, ist nirgendwo in <math>\mathbb{Q}</math> stetig. | Da <math>\delta</math> beliebig gewählt war, kann <math>g</math> nicht stetig in <math>x_0</math> sein. Da <math>x_0</math> beliebig gewählt war, ist nirgendwo in <math>\mathbb{Q}</math> stetig. | ||
| Zeile 109: | Zeile 128: | ||
{| class="wikitable left mw-collapsible mw-collapsed font-size: 100%;" | {| class="wikitable left mw-collapsible mw-collapsed font-size: 100%;" | ||
| − | | style="text-align:left; font-size: 100%;" | '''Beweis der Stetigkeit''' | + | | style="text-align:left; font-size: 100%;" | '''Beweis der Stetigkeit in den irrationalen Zahlen''' |
|- | |- | ||
| − | | Nun zeigen wir, dass <math>g</math> in den irrationalen Zahlen stetig ist. Sei dafür <math>x \in \mathbb{R}\setminus\mathbb{Q}</math> eine beliebige irrationale Zahl und <math>\varepsilon \gt 0</math>. Nun setze man <math>\delta_1 = \varepsilon</math>. Weiter bezeichne <math>M_{\delta_1} := \{y \in (x_0 - \delta_1, x_0 + \delta_1) | \varepsilon \leq |g(y) - g(x_0)| = |g(y)|\}</math> die Menge aller Punkte im Intervall <math>(x_0 - \delta_1, x_0 + \delta_1)</math>, die die | + | | Nun zeigen wir, dass <math>g</math> in den irrationalen Zahlen stetig ist. |
| + | |||
| + | Sei dafür <math>x \in \mathbb{R}\setminus\mathbb{Q}</math> eine beliebige irrationale Zahl und <math>\varepsilon \gt 0</math>. | ||
| + | |||
| + | Nun setze man <math>\delta_1 = \varepsilon</math>. Weiter bezeichne <math>M_{\delta_1} := \{y \in (x_0 - \delta_1, x_0 + \delta_1) | \varepsilon \leq |g(y) - g(x_0)| = |g(y)|\}</math> die Menge aller Punkte im Intervall <math>(x_0 - \delta_1, x_0 + \delta_1)</math>, die die ''Stetigkeitsungleichung'' <math>|g(y) - g(x_0)| \leq \varepsilon</math> nicht erfüllen. | ||
| + | |||
| + | Per Konstruktion der Funktion <math>g</math>, gilt für die Menge <math>\mathbb{R}\setminus\mathbb{Q}</math> der irrationalen Zahlen bereits, dass <math>g\left(\mathbb{R}\setminus\mathbb{Q}\right) \equiv 0</math>, also <math>M_{\delta_1} \subseteq \mathbb{Q}</math>. | ||
| + | |||
| + | Sei nun also <math>x = \frac{p}{q} \in M_{\delta_1} \subseteq \mathbb{Q}</math>. Es gilt <math>\frac{1}{q} = g(x) = |g(x)| = |g(x) - g(x_0)| \geq \varepsilon</math>, also auch <math>q \leq \frac{1}{\varepsilon}</math>. | ||
| + | |||
| + | Da die Menge <math>N := \{n \in \mathbb{N} | n \leq \frac{1}{\varepsilon}\}</math> offensichtlich endlich ist, können nur endlich viele Nenner <math>q_1, q_2, ..., q_n \in N</math> in den (rationalen) Zahlen aus <math>M_{\delta_1}</math> vorkommen. Da <math>(x_0 - \delta_1, x_0 + \delta_1)</math> beschränkt ist, können somit nur endlich viele rationale Zahlen mit Nennern <math>q_1, q_2, ..., q_n</math> in <math>(x_0 - \delta_1, x_0 + \delta_1)</math> und somit in <math>M_{\delta_1}</math> sein. Da <math>M_{\delta_1}</math> in den rationalen Zahlen enthalten ist, ist <math>M_{\delta_1}</math> somit endlich. | ||
| − | + | Es kann also ohne Probleme ein <math>0 \lt \delta_0 \leq \delta_1</math> gefunden werden, sodass <math>(x_0 - \delta_0, x_0 + \delta_0) \cap M_{\delta_1} = \emptyset</math>. | |
Per Konstruktion von <math>M_{\delta_1}</math> und <math>\delta_0</math> gilt nun insbesondere, dass <math>g((x_0 - \delta_0, x_0 + \delta_0)) \subseteq (g(x_0) - \varepsilon, g(x_0) + \varepsilon)</math>. Da <math>\varepsilon</math> beliebig gewählt war, ist <math>g</math> in <math>x_0</math> stetig. Da <math>x_0</math> beliebig (aus den irrationalen Zahlen <math>\mathbb{R}\setminus\mathbb{Q}</math>) gewählt war, ist <math>g</math> in den irrationalen Zahlen <math>\mathbb{R}\setminus\mathbb{Q}</math> stetig. | Per Konstruktion von <math>M_{\delta_1}</math> und <math>\delta_0</math> gilt nun insbesondere, dass <math>g((x_0 - \delta_0, x_0 + \delta_0)) \subseteq (g(x_0) - \varepsilon, g(x_0) + \varepsilon)</math>. Da <math>\varepsilon</math> beliebig gewählt war, ist <math>g</math> in <math>x_0</math> stetig. Da <math>x_0</math> beliebig (aus den irrationalen Zahlen <math>\mathbb{R}\setminus\mathbb{Q}</math>) gewählt war, ist <math>g</math> in den irrationalen Zahlen <math>\mathbb{R}\setminus\mathbb{Q}</math> stetig. | ||
| Zeile 119: | Zeile 148: | ||
=== Die Cantor-Funktion === | === Die Cantor-Funktion === | ||
| − | Die [[Cantor-Menge#Cantorfunktion|Cantor-Funktion]] <math>f: [0,1] \rightarrow [0,1]</math> ist ein Funktion, die auf der ebenso unintuitiven [[Cantor-Menge]] <math>C \subset [0,1]</math> aufbaut und folgende Eigenschaften besitzt: | + | Die '''[[Cantor-Menge#Cantorfunktion|Cantor-Funktion]]''' <math>f: [0,1] \rightarrow [0,1]</math> ist ein Funktion, die auf der ebenso unintuitiven [[Cantor-Menge]] <math>C \subset [0,1]</math> aufbaut und folgende Eigenschaften besitzt: |
| − | # Sie ist monoton wachsend, beginnend | + | # Sie ist monoton wachsend, beginnend bei <math>f(0) = 0</math> und endend bei <math>f(1) = 1</math>. |
# Sie ist in den Punkten <math>[0,1] \setminus C</math> differenzierbar und ihre Ableitung besitzt dort jeweils den Wert <math>0</math>. | # Sie ist in den Punkten <math>[0,1] \setminus C</math> differenzierbar und ihre Ableitung besitzt dort jeweils den Wert <math>0</math>. | ||
| − | === Die Indikatorfunktion der rationalen Zahlen | + | === Die Indikatorfunktion der rationalen Zahlen=== |
| − | Ein letztes Gegenbeispiel der Analysis | + | Ein letztes Gegenbeispiel der Analysis ist die '''[https://de.wikipedia.org/wiki/Indikatorfunktion Indikatorfunktion]''' <math>\chi_{\mathbb{Q}}: \mathbb{R} \rightarrow \{0,1\}, x \mapsto \begin{cases}1 & \text{für } x \in \mathbb{Q} \\ 0 & \text{für } x \in \mathbb{R}\setminus\mathbb{Q}\end{cases}</math> '''der rationalen Zahlen <math>\mathbb{Q}</math> in den reellen Zahlen <math>\mathbb{R}</math>''', welche die Unterschiedlichkeit der [https://de.wikipedia.org/wiki/Lebesgue-Integral Lebesgue]- und [https://de.wikipedia.org/wiki/Riemannsches_Integral Riemann]-Integrierbarkeit zeigt. |
Denn für ebendiese Funktion <math>\chi_{\mathbb{Q}}</math> lässt sich zeigen, dass sie: | Denn für ebendiese Funktion <math>\chi_{\mathbb{Q}}</math> lässt sich zeigen, dass sie: | ||
| Zeile 133: | Zeile 162: | ||
| style="text-align:left; font-size: 100%;" | '''Beweis der Lebesgue-Integrierbarkeit''' | | style="text-align:left; font-size: 100%;" | '''Beweis der Lebesgue-Integrierbarkeit''' | ||
|- | |- | ||
| − | | Nach der Definition des Lebesgue-Integrals gilt bereits: <math>\int_\mathbb{R} \chi_\mathbb{Q} \mathrm{d}\mathbb{\lambda} = \mathbb{\lambda}\left(\mathbb{Q}\right) = 0</math>. Insbesondere ist <math>\chi_\mathbb{Q}</math> also Lebesque-integrierbar. | + | | Nach der Definition des Lebesgue-Integrals gilt bereits: <math>\int_\mathbb{R} \chi_\mathbb{Q} \mathrm{d}\mathbb{\lambda} = \mathbb{\lambda}\left(\mathbb{Q}\right) = 0</math>. Insbesondere ist <math>\chi_\mathbb{Q}</math> also Lebesque-integrierbar.<ref>Jürgen Elstrodt: ''Maß- und Integrationstheorie'', Kapitel IV, §1. Integration von Treppenfunktionen, 1.2 Definition</ref> |
|} | |} | ||
{| class="wikitable left mw-collapsible mw-collapsed font-size: 100%;" | {| class="wikitable left mw-collapsible mw-collapsed font-size: 100%;" | ||
| − | | style="text-align:left; font-size: 100%;" | '''Beweis der Riemann-Integrierbarkeit''' | + | | style="text-align:left; font-size: 100%;" | '''Beweis der Nicht-Riemann-Integrierbarkeit''' |
|- | |- | ||
| − | | Bekanntermaßen impliziert die Riemann-Integrierbarkeit einer Funktion <math>f</math>, dass sie der gleichmäßige Grenzwert einer Folge <math>(t_n)_{n \in \mathbb{N}}</math> von Treppenfunktionen ist, also <math>\lim\limits_{n \rightarrow \infty}\|f - t_n\|_\infty = \lim\limits_{n \rightarrow \infty}\sup\limits_{x \in \mathbb{R}}|f(x) - t_n(x)| = 0</math> gilt. | + | | Bekanntermaßen impliziert die Riemann-Integrierbarkeit einer Funktion <math>f</math>, dass sie der gleichmäßige Grenzwert einer Folge <math>(t_n)_{n \in \mathbb{N}}</math> von Treppenfunktionen ist, also <math>\lim\limits_{n \rightarrow \infty}\|f - t_n\|_\infty = \lim\limits_{n \rightarrow \infty}\sup\limits_{x \in \mathbb{R}}|f(x) - t_n(x)| = 0</math> gilt. <ref>Winfried Kohnen: ''Analysis 1: Vorlesung von Prof. Dr. Kohnen'', Kapitel 6.2, Bermerkung, i)</ref> |
| − | Betrachtet man nun die Funktion <math>f = \chi_\mathbb{Q}</math>, so sieht man schnell ein, dass diese kein gleichmäßiger Grenzwert von Treppenfunktionen sein kann, da für jede beliebige Treppenfunktion mit beliebigen Stützpunkten und beliebigen Werten zwischen diesen Stützpunkten immer <math>\lim\limits_{n \rightarrow \infty}\|\chi_\mathbb{Q} - t_n\|_\infty \geq \frac{1}{2} \neq 0</math> gilt. | + | Betrachtet man nun die Funktion <math>f = \chi_\mathbb{Q}</math>, so sieht man schnell ein, dass diese kein gleichmäßiger Grenzwert von Treppenfunktionen sein kann, da für jede beliebige Treppenfunktion mit beliebigen Stützpunkten und beliebigen Werten zwischen diesen Stützpunkten immer <math>\lim\limits_{n \rightarrow \infty}\|\chi_\mathbb{Q} - t_n\|_\infty \geq \frac{1}{2} \neq 0</math> gilt. |
| + | |||
| + | Dies liegt daran, dass in dem Intervall zwischen zwei Stützpunkten einer Treppenfunktion (auf dem die Treppenfunktion per Definition konstant einen Wert <math>w \in \mathbb{R}</math> annimmt) jeweils eine rationale Zahl <math>x \in \mathbb{Q}</math> und eine irrationale Zahl <math>y \in \mathbb{R}\setminus\mathbb{Q}</math> mit <math>\chi_\mathbb{Q}(x) = 1</math> und <math>\chi_\mathbb{Q}(y) = 0</math> liegen. Offensichtlich gilt nun <math>max\{|\chi_\mathbb{Q}(x) - w|, |\chi_\mathbb{Q}(y) - w|\} \geq \frac{1}{2}</math>. | ||
|} | |} | ||
| + | |||
| + | == Siehe auch == | ||
| + | * Cantor-Funktion | ||
| + | |||
| + | == Literatur == | ||
| + | * Jürgen Appell: ''Analysis in Beispielen und Gegenbeispielen: Eine Einführung in die Theorie der reellen Zahlen'', Springer-Verlag, Berlin [u.a.], 2009, ISBN 978-3-540-88902-1 | ||
| + | * Bernard R. Gelbaum und John M. H. Olmsted: ''Counterexamples in Analysis'', Dover Publications, Mineola.], 2003, ISBN 978-0486428758 | ||
| + | |||
| + | == Einzelnachweise == | ||
| + | <references /> | ||
Aktuelle Version vom 7. April 2021, 00:19 Uhr
Willkommen auf meiner Benutzerseite für das Wiki-Projekt "Fun Facts" der Uni Heidelberg!
Hier findet sich ein Prototyp meines Teiles des Wiki-Artikels Gegenbeispiele der Funktionentheorie und Analysis.
Motivation
Die Untersuchung von Gegenbeispielen lässt sich unter anderem durch folgende drei Punkte motivieren:
- Gegenbeispiele können naheliegende und "intuitiv richtige" Aussage, die tatsächlich nicht gelten, widerlegen. So zeigt die Weierstraß-Funktion , dass Stetigkeit auf einem Intervall nicht Differenzierbarkeit in (irgend-)einem Punkt implizieren muss.
- Weiter können diese beweisen, dass zwei Definitionen verschieden sind, und, je nach Situation, möglicherweise auch, wodrin diese Unterschiede liegen. So zeigt die Indikatorfunktion der rationalen Zahlen (in den reellen Zahlen), die Lebesgue-integrierbar, aber nicht Riemann-integrierbar ist, dass diese beiden Definition der Integrierbarkeit/des Integrals nicht zusammenfallen können.
- Schließlich zeigen Gegenbeispiele (einer bestimmten Aussage) meist pathologische Sonderfälle auf, die durch geschickte Wahl der Definition und Voraussetzung der Aussage ausgeschlossen werden können.
Gegenbeispiele der Analysis
Neben der Funktionentheorie und der Topologie lassen sich auch in der Analysis viele Gegenbeispiele finden.
Die Weierstraß-Funktion [1]
Die Weierstraß-Funktion [math]f:\mathbb{R} \rightarrow \mathbb{R}[/math] ist eine stetige Funktion, die in keinem Punkt differenzierbar ist.
Zur Definition wähle man [math]a \in (0,1)[/math] und [math]b \in \mathbb{N}[/math] ungerade, sodass [math]ab \gt 1 + \frac{3\pi}{2}[/math]. Dann ist die Weierstraß-Funktion durch [math]f: \mathbb{R} \rightarrow \mathbb{R}, x \mapsto \sum\limits_{n = 0}^{\infty} a^n \cos\left(b^n \pi x\right)[/math] gegeben.
Man kann zeigen, dass
- die Weierstraß-Funktion [math]f[/math] stetig ist.
- die Weierstraß-Funktion [math]f[/math] in keinem Punkt differenzierbar ist.
| Beweis der Stetigkeit |
| Man betrachte die Weierstraß-Funktion als Funktionenreihe der Funktionen [math]\left(f_n: \mathbb{R} \rightarrow \mathbb{R}, x \mapsto a^n \cos\left(b^n\pi x\right)\right)_{n \in \mathbb{N}}[/math], die jeweils stetig in [math]x[/math] sind und der Abschätzung [math]|a^n \cos\left(b^n\pi x\right)| \leq |a^n| \leq a^n[/math] genügen.
Als geometrische Reihe konvergiert [math]\sum\limits_{n = 0}^{\infty} a^n = \frac{1}{1 - a}[/math], sodass (über den Majorantensatz von Weierstraß) auch die Funktionenreihe [math]\sum\limits_{n = 0}^{\infty} a^n\cos\left(b^n\pi x\right)[/math] gleichmäßig auf [math]\mathbb{R}[/math] konvergiert. Nimmt man beide obigen Aussagen zusammen, so folgt bereits, dass die Weierstraß-Funktion als gleichmäßig konvergente Funktionsreihe stetiger Funktionen selbst stetig ist. [2] |
| Beweis der Nicht-Differenzierbarkeit |
| Sei nun [math]x_0 \in \mathbb{R}[/math] ein beliebiger Punkt. Um zu zeigen, dass in diesem Punkt die Ableitung der Weierstraß-Funktion, also der Grenzwert [math]\lim\limits_{x \to x_0} \frac{f(x) - f(x_0)}{x - x_0}[/math], nicht existiert, reicht es eine Folge zu finden, die gegen [math]x_0[/math] konvergiert, während der dazugehörige Differenzenquotient keinen Grenzwert in [math]\mathbb{R}[/math] besitzt.
Man wähle nun für jedes [math]m \in \mathbb{N}[/math] die eindeutige ganze Zahl [math]c_m \in \mathbb{Z}[/math], sodass [math]b^m x_0 - c_m \in \left(-\frac{1}{2}, \frac{1}{2}\right][/math] gilt. Weiter definiere man für jedes [math]m \in \mathbb{N}[/math] die reellen Zahlen [math]x_m := b^m x_0 - c_m[/math] und [math]y_m := \frac{c_m - 1}{b^m}[/math]. Für diese gelten die Ungleichung [math]y_m - x_0 = - \frac{1 + x_m}{b^m} \lt 0 [/math], also [math]y_m \lt x_0[/math]. Insbesondere folgt nun:
Die Folge [math](y_m)_{m \in \mathbb{N}}[/math] konvergiert also von unten gegen [math]x_0[/math].
[math]\phantom{=}\frac{f(y_m) - f(x_0)}{y_m - x_0} = \frac{\sum\limits_{n = 0}^{\infty}a^n\cos\left(b^n\pi y_m\right) - \sum\limits_{n = 0}^{\infty}a^n\cos\left(b^n\pi x_0\right)}{y_m - x_0} \\ = \sum\limits_{n = 0}^{\infty} a^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{y_m - x_0} \\ = \sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)} + \sum\limits_{n = m}^{\infty} a^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{y_m - x_0} \\ = \sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)} + \sum\limits_{n = 0}^{\infty} a^{n + m} \frac{\cos\left(b^{n + m}\pi y_m\right) - \cos\left(b^{n + m}\pi x_0\right)}{y_m - x_0} [/math].
[math]\phantom{=}\sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)}\\ =\sum\limits_{n = 0}^{m - 1} \frac{-2(ab)^n }{b^n(y_m - x_0)}\sin\left(\frac{b^n\pi(y_m + x_0)}{2}\right)\sin\left(\frac{b^n\pi(y_m - x_0)}{2}\right) \\ = \sum\limits_{n = 0}^{m - 1}-\pi(ab)^n\sin\left(\frac{b^n\pi(y_m + x_0)}{2}\right)\frac{\sin\left(\frac{b^n\pi(y_m - x_0)}{2}\right)}{\frac{b^n\pi(y_m - x_0)}{2}} [/math]. Verwendet man nun die Dreiecks-Ungleichung und den Fakt, dass [math]\left|\frac{\sin(x)}{x}\right| \leq 1[/math] für alle [math]x \in \mathbb{R}\setminus\{0\}[/math], so ergibt sich weiter die Abschätzung: [math]\phantom{=}\left|\sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)}\right| \leq \sum\limits_{n = 0}^{m - 1}\pi (ab)^n = \pi\frac{(ab)^m - 1}{ab - 1} \lt \pi \frac{(ab)^m}{ab - 1}[/math]. Es existiert also ein [math]\epsilon \in (-1, 1)[/math], sodass [math]\sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)} = \epsilon \pi \frac{(ab)^m}{ab - 1}[/math].
Und mit dem trigonometrischen Additionstheorem für den Kosinus erhält man:
[math]\phantom{=}\sum\limits_{n = 0}^{\infty} a^{n + m} \frac{\cos\left(b^{n + m}\pi y_m\right) - \cos\left(b^{n + m}\pi x_0\right)}{y_m - x_0} \\ = \sum\limits_{n = 0}^{\infty} a^{n + m} \frac{-(-1)^{c_m} - (-1)^{c_m}\cos\left(b^n\pi x_m\right)}{y_m - x_0} \\ = \sum\limits_{n = 0}^{\infty} a^{n + m}(-1)(-1)^{c_m} \frac{1 + \cos\left(b^n\pi x_m\right)}{-\frac{1 + x_m}{b^n}} \\ = (ab)^m(-1)^{c_m}\sum\limits_{n = 0}^{\infty} a^{n} \frac{1 + \cos\left(b^n\pi x_m\right)}{1 + x_m}. [/math]
[math]\phantom{=}\sum\limits_{n = 0}^{\infty} a^n \frac{1 + \cos\left(b^n\pi x_m\right)}{1 + x_m} \geq \frac{1 + \cos\left(\pi x_m\right)}{1 + x_m} \geq \frac{1}{1 + \frac{1}{2}} = \frac{2}{3}[/math], es gibt also ein [math]\eta \geq 1[/math], sodass [math](ab)^m(-1)^{c_m}\sum\limits_{n = 0}^{\infty} a^{n} \frac{1 + \cos\left(b^n\pi x_m\right)}{1 + x_m} = \frac{2}{3}(ab)^m(-1)^{c_m}\eta[/math].
[math]\phantom{=}\frac{f(y_m) - f(x_0)}{y_m - x_0} = \sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)} + \sum\limits_{n = 0}^{\infty} a^{n + m} \frac{\cos\left(b^{n + m}\pi y_m\right) - \cos\left(b^{n + m}\pi x_0\right)}{y_m - x_0} = \epsilon\frac{\pi(ab)^m}{ab - 1} + \frac{2}{3}(ab)^m(-1)^{c_m}\eta = (-1)^{c_m}(ab)^m\eta\left(\frac{2}{3} + (-1)^{c_m}\frac{\epsilon}{\eta}\frac{\pi}{ab - 1}\right)[/math].
[math]\phantom{=}\frac{2}{3} + (-1)^{c_m}\frac{\epsilon}{\eta}\frac{\pi}{ab - 1} \gt \frac{2}{3} - \frac{\pi}{ab - 1} \gt 0[/math].
[math]\phantom{=}\left|\frac{f(y_m) - f(x_0)}{y_m - x_0}\right| \gt (ab)^m\left(\frac{2}{3} - \frac{\pi}{ab - 1}\right) \rightarrow \infty[/math], sodass [math]f[/math] nicht in [math]x_0[/math] differenzierbar sein kann. Da [math]x_0[/math] beliebig gewählt war, ist die Weierstraß-Funktion [math]f[/math] also nirgendwo differenzierbar. |
Die modifizierte Dirichlet-Funktion[3]
Eine weitere interessante Funktion, die das intuitive Verständnis der Stetigkeit herausfordert, ist die modifizierte Dirichlet-Funktion. Diese ist teilweise auch als thomaesche Funktion bekannt.
Diese ist definiert durch [math]g: \mathbb{R} \rightarrow \mathbb{R}, x \mapsto \begin{cases}\frac{1}{q} & \text{für } x = \frac{p}{q} \in \mathbb{Q} \\ 0 & \text{für } x \in \mathbb{R}\setminus\mathbb{Q} \end{cases}[/math], sodass die Funktion folgende sonderbaren Eigenschaften hat:
- Sie ist in den rationalen Zahlen [math]\mathbb{Q}[/math] unstetig.
- Sie ist in den irrationalen Zahlen [math]\mathbb{R}\setminus\mathbb{Q}[/math] stetig.
| Beweis der Unstetigkeit in den rationalen Zahlen |
| Wir zeigen zuerst die Unstetigkeit in den rationalen Zahlen.
Dafür sei [math]x \in \mathbb{Q}[/math] eine beliebige rationale Zahl, sowie [math]p \in \mathbb{Z}, q \in \mathbb{N}[/math] die (eindeutigen) teilerfremden ganzen Zahlen, sodass [math]x = \frac{p}{q}[/math]. Damit gilt dann: [math]g(x_0) = \frac{1}{q}[/math]. Sei nun [math]0 \lt \epsilon \leq \frac{1}{q}[/math]. Es ist bekannt, dass für jedes [math]\delta \in \mathbb{R}_{\gt 0}[/math] unendlich viele irrationale Zahlen in der Umgebung [math]U_\delta (x_0) = (x_0 - \delta, x_0 + \delta)[/math] liegen. Für eine beliebige irrationale Zahl [math]x \in U_\delta (x_0) \cap \mathbb{R}\setminus\mathbb{Q}[/math] gilt nun: [math]|f(x_0) - f(x)| = |\frac{1}{q} - 0| = \frac{1}{q} \geq \varepsilon[/math]. Da [math]\delta[/math] beliebig gewählt war, kann [math]g[/math] nicht stetig in [math]x_0[/math] sein. Da [math]x_0[/math] beliebig gewählt war, ist nirgendwo in [math]\mathbb{Q}[/math] stetig. |
| Beweis der Stetigkeit in den irrationalen Zahlen |
| Nun zeigen wir, dass [math]g[/math] in den irrationalen Zahlen stetig ist.
Sei dafür [math]x \in \mathbb{R}\setminus\mathbb{Q}[/math] eine beliebige irrationale Zahl und [math]\varepsilon \gt 0[/math]. Nun setze man [math]\delta_1 = \varepsilon[/math]. Weiter bezeichne [math]M_{\delta_1} := \{y \in (x_0 - \delta_1, x_0 + \delta_1) | \varepsilon \leq |g(y) - g(x_0)| = |g(y)|\}[/math] die Menge aller Punkte im Intervall [math](x_0 - \delta_1, x_0 + \delta_1)[/math], die die Stetigkeitsungleichung [math]|g(y) - g(x_0)| \leq \varepsilon[/math] nicht erfüllen. Per Konstruktion der Funktion [math]g[/math], gilt für die Menge [math]\mathbb{R}\setminus\mathbb{Q}[/math] der irrationalen Zahlen bereits, dass [math]g\left(\mathbb{R}\setminus\mathbb{Q}\right) \equiv 0[/math], also [math]M_{\delta_1} \subseteq \mathbb{Q}[/math]. Sei nun also [math]x = \frac{p}{q} \in M_{\delta_1} \subseteq \mathbb{Q}[/math]. Es gilt [math]\frac{1}{q} = g(x) = |g(x)| = |g(x) - g(x_0)| \geq \varepsilon[/math], also auch [math]q \leq \frac{1}{\varepsilon}[/math]. Da die Menge [math]N := \{n \in \mathbb{N} | n \leq \frac{1}{\varepsilon}\}[/math] offensichtlich endlich ist, können nur endlich viele Nenner [math]q_1, q_2, ..., q_n \in N[/math] in den (rationalen) Zahlen aus [math]M_{\delta_1}[/math] vorkommen. Da [math](x_0 - \delta_1, x_0 + \delta_1)[/math] beschränkt ist, können somit nur endlich viele rationale Zahlen mit Nennern [math]q_1, q_2, ..., q_n[/math] in [math](x_0 - \delta_1, x_0 + \delta_1)[/math] und somit in [math]M_{\delta_1}[/math] sein. Da [math]M_{\delta_1}[/math] in den rationalen Zahlen enthalten ist, ist [math]M_{\delta_1}[/math] somit endlich. Es kann also ohne Probleme ein [math]0 \lt \delta_0 \leq \delta_1[/math] gefunden werden, sodass [math](x_0 - \delta_0, x_0 + \delta_0) \cap M_{\delta_1} = \emptyset[/math]. Per Konstruktion von [math]M_{\delta_1}[/math] und [math]\delta_0[/math] gilt nun insbesondere, dass [math]g((x_0 - \delta_0, x_0 + \delta_0)) \subseteq (g(x_0) - \varepsilon, g(x_0) + \varepsilon)[/math]. Da [math]\varepsilon[/math] beliebig gewählt war, ist [math]g[/math] in [math]x_0[/math] stetig. Da [math]x_0[/math] beliebig (aus den irrationalen Zahlen [math]\mathbb{R}\setminus\mathbb{Q}[/math]) gewählt war, ist [math]g[/math] in den irrationalen Zahlen [math]\mathbb{R}\setminus\mathbb{Q}[/math] stetig. |
Die Cantor-Funktion
Die Cantor-Funktion [math]f: [0,1] \rightarrow [0,1][/math] ist ein Funktion, die auf der ebenso unintuitiven Cantor-Menge [math]C \subset [0,1][/math] aufbaut und folgende Eigenschaften besitzt:
- Sie ist monoton wachsend, beginnend bei [math]f(0) = 0[/math] und endend bei [math]f(1) = 1[/math].
- Sie ist in den Punkten [math][0,1] \setminus C[/math] differenzierbar und ihre Ableitung besitzt dort jeweils den Wert [math]0[/math].
Die Indikatorfunktion der rationalen Zahlen
Ein letztes Gegenbeispiel der Analysis ist die Indikatorfunktion [math]\chi_{\mathbb{Q}}: \mathbb{R} \rightarrow \{0,1\}, x \mapsto \begin{cases}1 & \text{für } x \in \mathbb{Q} \\ 0 & \text{für } x \in \mathbb{R}\setminus\mathbb{Q}\end{cases}[/math] der rationalen Zahlen [math]\mathbb{Q}[/math] in den reellen Zahlen [math]\mathbb{R}[/math], welche die Unterschiedlichkeit der Lebesgue- und Riemann-Integrierbarkeit zeigt.
Denn für ebendiese Funktion [math]\chi_{\mathbb{Q}}[/math] lässt sich zeigen, dass sie:
- Lebesgue-integrierbar ist.
- nicht Riemann-integrierbar ist.
| Beweis der Lebesgue-Integrierbarkeit |
| Nach der Definition des Lebesgue-Integrals gilt bereits: [math]\int_\mathbb{R} \chi_\mathbb{Q} \mathrm{d}\mathbb{\lambda} = \mathbb{\lambda}\left(\mathbb{Q}\right) = 0[/math]. Insbesondere ist [math]\chi_\mathbb{Q}[/math] also Lebesque-integrierbar.[4] |
| Beweis der Nicht-Riemann-Integrierbarkeit |
| Bekanntermaßen impliziert die Riemann-Integrierbarkeit einer Funktion [math]f[/math], dass sie der gleichmäßige Grenzwert einer Folge [math](t_n)_{n \in \mathbb{N}}[/math] von Treppenfunktionen ist, also [math]\lim\limits_{n \rightarrow \infty}\|f - t_n\|_\infty = \lim\limits_{n \rightarrow \infty}\sup\limits_{x \in \mathbb{R}}|f(x) - t_n(x)| = 0[/math] gilt. [5]
Betrachtet man nun die Funktion [math]f = \chi_\mathbb{Q}[/math], so sieht man schnell ein, dass diese kein gleichmäßiger Grenzwert von Treppenfunktionen sein kann, da für jede beliebige Treppenfunktion mit beliebigen Stützpunkten und beliebigen Werten zwischen diesen Stützpunkten immer [math]\lim\limits_{n \rightarrow \infty}\|\chi_\mathbb{Q} - t_n\|_\infty \geq \frac{1}{2} \neq 0[/math] gilt. Dies liegt daran, dass in dem Intervall zwischen zwei Stützpunkten einer Treppenfunktion (auf dem die Treppenfunktion per Definition konstant einen Wert [math]w \in \mathbb{R}[/math] annimmt) jeweils eine rationale Zahl [math]x \in \mathbb{Q}[/math] und eine irrationale Zahl [math]y \in \mathbb{R}\setminus\mathbb{Q}[/math] mit [math]\chi_\mathbb{Q}(x) = 1[/math] und [math]\chi_\mathbb{Q}(y) = 0[/math] liegen. Offensichtlich gilt nun [math]max\{|\chi_\mathbb{Q}(x) - w|, |\chi_\mathbb{Q}(y) - w|\} \geq \frac{1}{2}[/math]. |
Siehe auch
- Cantor-Funktion
Literatur
- Jürgen Appell: Analysis in Beispielen und Gegenbeispielen: Eine Einführung in die Theorie der reellen Zahlen, Springer-Verlag, Berlin [u.a.], 2009, ISBN 978-3-540-88902-1
- Bernard R. Gelbaum und John M. H. Olmsted: Counterexamples in Analysis, Dover Publications, Mineola.], 2003, ISBN 978-0486428758
Einzelnachweise
- ↑ https://math.berkeley.edu/~brent/files/104_weierstrass.pdf
- ↑ Winfried Kohnen: Analysis 1: Vorlesung von Prof. Dr. Kohnen, Kapitel 5.4, Satz 4
- ↑ Jürgen Appell, op. cit., Beispiel 1.12
- ↑ Jürgen Elstrodt: Maß- und Integrationstheorie, Kapitel IV, §1. Integration von Treppenfunktionen, 1.2 Definition
- ↑ Winfried Kohnen: Analysis 1: Vorlesung von Prof. Dr. Kohnen, Kapitel 6.2, Bermerkung, i)