Banach-Tarski-Paradox: Unterschied zwischen den Versionen
| (40 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
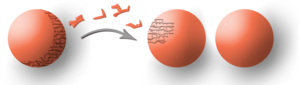
[[Datei:Doubling of a sphere, as per the Banach-Tarski Theorem.png|mini|alternativtext=|Verdopplung eines Balles nach Banach-Tarski.]] | [[Datei:Doubling of a sphere, as per the Banach-Tarski Theorem.png|mini|alternativtext=|Verdopplung eines Balles nach Banach-Tarski.]] | ||
| − | Das '''Banach-Tarski-Paradoxon''' (eng. Banach-Tarski-Paradox) oder auch '''Satz von Banach und Tarski''' ist ein Satz aus der geometrische Mengenlehre, welcher die Grenzen des anschaulichen Volumenbegriffs deutlich macht. | + | Das '''Banach-Tarski-Paradoxon''' (eng. Banach-Tarski-Paradox) oder auch '''Satz von Banach und Tarski''' ist ein Satz aus der geometrische Mengenlehre, welcher die Grenzen des anschaulichen Volumenbegriffs deutlich macht. Sei eine Kugel in drei oder mehr Dimensionen gegeben, existiert nach dem Satz eine Zerlegung der Kugel in endlich viele disjunkte Teilmengen bzw. Teile, sodass sich aus den Teilen zwei Kugeln mit demselben Radius wie die ursprüngliche Kugel konstruieren lassen. Dadurch verdoppelt sich das Volumen unersichtlich (denn eine Kugel wurde in zwei genauso große zerteilt). Dieses Paradoxon veranschaulicht somit, dass das mathematische Modell des Raumes in der Mathematik die Realität nicht in allen Eigenschaften widerspiegelt. |
| − | Im Gegensatz zu vielen anderen Sätzen aus der Geometrie ist der | + | Im Gegensatz zu vielen anderen Sätzen aus der Geometrie, ist der Banach-Tarski Satz ziemlich abhängig von der Wahl des angemessenen Axiomgesetzes. Das Axiom der Wahl (eng. Axiom of Choice) erlaubt für einen Beweis, da überabzählbar viele Wahlen getroffen werden müssen. Dies folgt aus der Natur der Teilmengen in welche man den Ball zerlegt, diese sind nämlich unendlich filigran bzw. staubwolkenartig (siehe Löwenzahn<ref>https://funfacts.mathi.uni-heidelberg.de/index.php/Datei:Dandelion_(107276119).jpg</ref>). Eine andere Auswahl an Axiomen ergibt aber, dass eine solche Zerlegung und Rekonstruktion der Kugel nicht möglich sind. |
== Vorwissen == | == Vorwissen == | ||
| − | === Hilberts Hotel | + | === Hilberts Hotel === |
| − | [[Hilberts Hotel]] (eng. Hilbert's Paradox of the Grand Hotel) ist ein Gedankenexperiment, erschaffen von David Hilbert und eingeführt in seiner Vorlesung "Über das Unendliche" im Jahre 1924. Es demonstriert die | + | [[Hilberts Hotel]] (eng. Hilbert's Paradox of the Grand Hotel) ist ein Gedankenexperiment, erschaffen von David Hilbert und eingeführt in seiner Vorlesung "Über das Unendliche" im Jahre 1924. Es demonstriert die kontraintuitiven Eigenschaften des Unendlichen, wie z.B. die Eigenschaft, dass ein Hotel mit unendlichen Räumen und einem Gast pro Raum nicht voll besetzt ist und weitere Gäste problemlos einen Raum zugewiesen kriegen können. Die bei uns wichtigere Eigenschaft ist, dass, wenn ein Gast das Hotel verlässt, alle anderen Gäste so umgeschoben werden können, dass wieder jeder Raum besetzt ist und das Hotel scheinbar wieder vollgebucht ist. |
Da Hilberts Hotel in der Vorlesung besprochen wurde und auch schon von einer anderen Gruppe behandelt wird, werden wir den Artikel [[Hilberts Hotel]] hier verlinken. | Da Hilberts Hotel in der Vorlesung besprochen wurde und auch schon von einer anderen Gruppe behandelt wird, werden wir den Artikel [[Hilberts Hotel]] hier verlinken. | ||
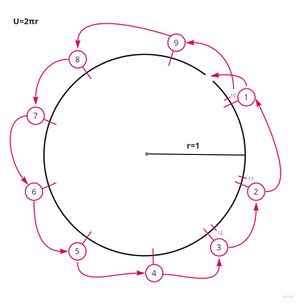
| + | [[Datei:Circle graphic updated 3.jpg|alternativtext=|mini|In einem Kreis lassen sich abzählbar viele Lücken füllen nur durch das Umordnen der existierenden Punkten.]] | ||
| + | Hilberts Hotel kann auch auf Formen angewandt werden. Wenn man aus einem Kreis einen einzigen Punkt entfernt (siehe Bild<ref>https://funfacts.mathi.uni-heidelberg.de/index.php/Datei:Circle_graphic_updated_3.jpg</ref>), entsteht scheinbar eine Lücke. Da aber der Umfang eines Kreises immer irrational ist (u = 2πr mit π irrational), kann man von der Lücke aus entlang dem Umfang Strecken von einer rationalen Länge (bsp. Länge r) abmessen und den entsprechenden Punkt markieren (den ersten mit 1, den zweiten mit 2 etc.). Am Ende des Prozesses hat man unendlich viele Punkte markiert, mit denen man entsprechend Hilberts Hotel die Lücke einfüllen kann: Punkt 1 füllt die Lücke, Punkt 2 füllt die Lücke, die durch Punkt 1 entstanden ist und so weiter. Somit ist also Hilberts Hotel auch anwendbar auf Formen und Körper. | ||
| − | + | === Hyperwebster === | |
| − | + | Der Hyperwebster<ref>https://www.latg.org/blog/2018/06/09/hyperwebster/</ref> ist eine Erfindung von Dr. Ian Steward, um zu veranschaulichen, wie groß unzählbare Unendlichkeit sein kann. | |
| − | + | Der Hyperwebster ist eine Version von Webster's Dictionary<ref>https://en.wikipedia.org/wiki/Webster%27s_Dictionary</ref>, wo jede mögliche Buchstabenkombination vorkommen soll. Man starte mit dem Buchstaben A, dann AA, dann AAA, und so weiter bis man unendlich viele A's hat. Danach kommt AB, ABA, ABAA, ABAAA, ..., AC, ..., AZ, ..., B, BA, BAA, ..., Z, ZA, ZAA etc. Am Ende sieht der Hyperwebster dann ungefähr so aus: | |
| − | |||
| − | |||
| − | Der Hyperwebster ist eine Version von Webster's Dictionary, wo jede mögliche Buchstabenkombination vorkommen soll. Man starte mit dem Buchstaben A, dann AA, dann AAA, und so weiter bis man unendlich viele A's hat. Danach kommt AB, ABA, ABAA, ABAAA, ..., AC, ..., AZ, ..., B, BA, BAA, ..., Z, ZA, ZAA etc. Am Ende sieht der Hyperwebster dann ungefähr so aus: | ||
A, AA, AAA, AAAA, ..., AB, ABA, ABAA, .... AAB, AABA, ..., AC, ... AZ, AZAA, ... | A, AA, AAA, AAAA, ..., AB, ABA, ABAA, .... AAB, AABA, ..., AC, ... AZ, AZAA, ... | ||
| Zeile 28: | Zeile 27: | ||
Nun haben wir ein Wörterbuch, welches jedes mögliche Wort, jeden möglichen Satz, jede mögliche Buchstabenkombination enthält. Der Verlag möchte jetzt dieses Wörterbuch ausdrucken, es wäre aber viel zu groß. Der Verlag fasst also alle Wörter in 26 Bände zusammen, somit werden alle Wörter mit einem bestimmten Anfangsbuchstaben in einen Band gepackt. | Nun haben wir ein Wörterbuch, welches jedes mögliche Wort, jeden möglichen Satz, jede mögliche Buchstabenkombination enthält. Der Verlag möchte jetzt dieses Wörterbuch ausdrucken, es wäre aber viel zu groß. Der Verlag fasst also alle Wörter in 26 Bände zusammen, somit werden alle Wörter mit einem bestimmten Anfangsbuchstaben in einen Band gepackt. | ||
| − | Um jetzt Platz zu sparen, nimmt der Verlag jeden Band und streicht den Anfangsbuchstaben jedes Wortes, da jeder Anfangsbuchstabe nur ein Mal pro Band vorkommt. Dabei stellt sich heraus | + | Um jetzt Platz zu sparen, nimmt der Verlag jeden Band und streicht den Anfangsbuchstaben jedes Wortes, da jeder Anfangsbuchstabe nur ein Mal pro Band vorkommt. Dabei stellt sich heraus, wenn man den Anfangsbuchstaben jedes Bandes kürzt, man wieder den Hyperwebster selbst erhält. Der Hyperwebster ist also in diesem Sinne ein sich selbst enthaltendes (selbstähnliches) Fraktal, da man durch die oben beschriebene Methode aus einem Hyperwebster gleich 26 machen kann. |
== Paradox == | == Paradox == | ||
| − | Der Banach-Tarski Satz widerspricht | + | Der Banach-Tarski Satz widerspricht der gängingen geometrischen Intuition und wird somit oft auch Banach-Tarski Paradoxon genannt. Nach Banach-Tarski wird ein Ball in zwei weitere Bälle mit demselben Volumen zerlegt ohne den Ball zu dehnen, biegen oder neue Punkte dem Ball hinzuzufügen. Tatsächlich werden die Teile, in welche der Ball zerlegt wird, nur rotiert und geschoben (entspricht einer Translation in der Mathematik). Es scheint unmöglich zu sein, durch diese Operationen das Volumen zu erhöhen, da sie, intuitiv betrachtet, das Volumen erhalten. Mathematisch ist es auch so, nur kann man dieselbe Intuition bei dieser Zerlegung des Balles nicht anwenden da für die Teile in welche der Ball zerlegt wird, kein Volumen definiert werden kann. |
| − | [[Datei:Dandelion (107276119).jpg|alternativtext=|mini|442x442px|Man kann sich die Teile in welche der Ball zerlegt wird jeweils als eine reife Löwenzahnpflanze vorstellen. Also, mathematisch gesehen, eine Sammlung an Punkten um einen Mittelpunkt zusammen mit dem Liniensegment, welcher den Punkt zum Mittelpunkt verbindet. Ein solches Konstrukt existiert in 3 Dimensionen hat aber kein Volumen.]]Nach dem Widerzusammenfügen der Teile lässt sich wieder ein Volumen definieren und nun ist es so dass das Volumen anders als das | + | [[Datei:Dandelion (107276119).jpg|alternativtext=|mini|442x442px|Man kann sich die Teile in welche der Ball zerlegt wird jeweils als eine reife Löwenzahnpflanze vorstellen. Also, mathematisch gesehen, eine Sammlung an Punkten um einen Mittelpunkt zusammen mit dem Liniensegment, welcher den Punkt zum Mittelpunkt verbindet. Ein solches Konstrukt existiert in 3 Dimensionen hat aber kein Volumen.]]Nach dem Widerzusammenfügen der Teile lässt sich wieder ein Volumen definieren und nun ist es so, dass das Volumen anders als das ursprüngliche Volumen ist (nämlich doppelt so groß). In der Realität lassen sich solche Umformungen leider nicht durchführen da der Ball in unendlich feine bzw. dünne Teile zerlegt werden müsste. |
| + | |||
| + | Eine allgemeinere Version des Satzes existiert, oft informell '''"pea and the Sun paradox"''' (dt. Das Erbse-Sonne Paradoxon) genannt. Diese besagt, dass eine Erbse in Stücke zerlegt werden kann und dass sich aus den entstehenden Stücken dann die Sonne konstruieren lässt<ref>https://plus.maths.org/content/pea-and-sun</ref>. | ||
| + | |||
| + | === Konsequenzen === | ||
| + | Die wichtigste Konsequenz des Paradoxons von Banach und Tarski besteht in der Einsicht, dass nicht allen Teilmengen von <math>\mathbb{R}^3</math> sinnvoll ein Volumen zugewiesen werden kann<ref>https://dmg.tuwien.ac.at/winkler/pub/bantar.pdf</ref>. Wobei unter '''sinnvoll''' das Erfüllen von manchen Eigenschaften, wie zum Beispiel die Bewegungsinvarianz, zu verstehen ist. Dies folgt aus Banach-Tarski, denn während der Zerlegung des Balles entstehen Teilmengen von <math>\mathbb{R}^3</math>, welche wie eine kugelförmige Punktwolke aussehen, wobei alle Punkten mit einem Strahl zum Mittelpunkt verbunden sind. Teilmengen dieser Form lässt sich kein Volumen widerspruchsfrei zuordnen<ref>https://dmg.tuwien.ac.at/winkler/pub/bantar.pdf</ref>. | ||
| + | |||
| + | == Geschichte, Satz von Banach und Tarski == | ||
| + | In einem in 1924 veröffentlichten Paper gaben [https://en.wikipedia.org/wiki/Stefan_Banach Stefan Banach] und [https://en.wikipedia.org/wiki/Alfred_Tarski Alfred Tarski] eine Konstruktion einer solchen paradoxischen Zerlegung, gegründet in der früheren Arbeit von Giuseppe Vitali. Banach und Tarski haben den folgenden, allgemeineren (auch stärkeren) Satz bewiesen: | ||
| + | |||
| + | :'''<u>Satz:</u>''' Sei <math>d \ge 3</math> eine ganze Zahl und seien <math>X, Y\subset \mathbb{R}^d</math> beschränkte Mengen mit nicht-leerem Inneren. Dann gibt es eine natürliche Zahl <math>n</math> und eine disjunkte Zerlegung <math>X_1, \dots, X_n</math> von <math>X</math> und zugehörige [https://de.wikipedia.org/wiki/Bewegung_(Mathematik) Bewegung] <math>\beta_1, \dots, \beta_n</math> derart, dass <math>Y</math> die disjunkte Vereinigung der Mengen <math>\beta_1(X_1), \dots, \beta_n(X_n)</math> ist. | ||
| + | |||
| + | Das heißt, dass in <math>\mathbb{R}^d:d\geq 3</math> eine beschränkte Menge mit nicht-leerem Inneren sich disjunkt zerlegen und dann in eine beliebige, beschränkte Menge mit nicht-leerem Inneren wieder disjunkt vereinigen lassen kann. Da wir die durch die Zerlegung konstruierte Teilmengen nur bewegen, werden keine neue Punkten erzeugt und die Abstände zwischen allen Punkten eines <math>X_j</math>werden paarweise erhalten. Somit folgt das Banach-Tarski-Paradoxon als ein bestimmter Fall: Sei die Menge <math>X</math> von oben ein Ball und die Menge <math>Y</math> zwei Kopien des Balles mit demselben Radius wie der Ball <math>X</math>. Dann gilt: <math>X,Y\subset \mathbb{R^3}</math>, da Bälle per Definition beschränkt sind und ein nichtleeres Innere haben. Nach dem Satz gilt, dass eine disjunkte Zerlegung <math>X_1,..., X_n</math> von <math>X</math> zusammen mit der zugehörigen Bewegung <math>\beta _1,..., \beta _n</math> existiert, sodass <math>Y=\beta _1(X_1)\dot\cup \beta _2(X_2)\ \dot\cup ... \dot\cup\ \beta _n(X_n)</math> gilt. | ||
| + | |||
| + | Der allgemeinere Satz von Banach und Tarski gilt in einer und zwei Dimensionen nicht, da die Bewegungsfreiheit in diesen Dimensionen zu beschränkt ist. Als Folge dessen besitzen alle Figuren, welche durch eine Zerlegung und eine zugehörige Bewegung der Teile, sich ineinander umformen lassen, denselben Flächeninhalt. Banach und Tarski haben aber gezeigt, dass, wenn Zerlegungen in abzählbar viele Teile (statt endlich viele) erlaubt sind, die analoge Version des Satzes immer noch gilt. | ||
| + | |||
| + | === Beweisskizze === | ||
| + | '''Anmerkung:''' hier erklären wir bloß die Grundzüge des Beweises, eine ausführlichere Beweisskizze finden Sie [https://de.wikipedia.org/wiki/Banach-Tarski-Paradoxon#Beweisskizze hier]. | ||
| + | |||
| + | Der Beweis benutzt die Tatsache, dass Drehungen im Raum mathematisch als Elemente einer Gruppe aufgefasst werden können. Somit kann man sie miteinander verknüpfen und auf andere Objekte anwenden, wobei die Bedingungen der Gruppe erfüllt sind: | ||
| + | :* Die Verknüpfung mehrerer Drehungen ist wiederum eine Drehung. | ||
| + | :* Die Verknüpfungsoperation ist assoziativ. | ||
| + | :* In einer Verknüpfungskette <math> g_1\dots\ g_i g_i^{-1}\dots\ g_n </math> eliminieren sich die benachbarten Elemente <math> g_{i} </math> und <math> g_{i}^{-1} </math>, da sie zueinander invers sind. Dies gilt für Drehungen ebenso. Drehungen operieren auf Punkten oder Punktmengen im Raum, indem sie deren Lage verändern. | ||
| + | Für den Beweis wird eine ganz besondere Gruppe betrachtet; Die freie Gruppe <math>F_2</math> mit ihren Erzeugern <math>a</math> und <math>b</math> besteht abstrakt definiert aus Wörtern über dem Alphabet (Alphabete sind Mengen von Buchstaben) <math>E:=\{a,a^{-1},b,b^{-1}\}</math>, in denen keine Elemente zu deren Inversen benachbart sind. Die Verknüpfung der Gruppe stellt die [https://de.wikipedia.org/wiki/Wort_(theoretische_Informatik)#Konkatenation Konkatenation] dar, wobei möglicherweise entstandene Invers-Paare iterativ entfernt werden, bis keine solchen Paare im verknüpften Wort mehr vorkommen. Das leere Wort <math>\varepsilon</math> stellt das neutrale Element der Gruppe dar. Die Darstellung jedes Elements von <math>F_2</math> als gekürztes Wort ist dabei eindeutig. | ||
| + | |||
| + | ==== Schritt I ==== | ||
| + | Wir definieren die Mengen <math>S(a), S(b), S(a^{-1}), S(b^{-1})</math>. | ||
| + | Hier ist <math>S(a)</math> die Menge aller Wörter aus <math>F_2</math>, die links mit <math>a</math> beginnen, z.B.:<math>ab, abb,aba^{-1}</math>. Die anderen S-Mengen sind analog definiert. Wir fordern wir oben dass die Darstellung der Wörter gekürzt ist, also <math>a</math> und <math>a^{-1}</math> kommen nicht nebeneinander vor. | ||
| + | |||
| + | ==== Schritt II ==== | ||
| + | Wie zeigen dass eine paradoxe Zerlegung von <math>F_2</math> existiert. | ||
| + | Neben der üblichen Zerlegung: <math>F_2={e}\cup S(a)\cup S(a^{-1})\cup S(b)\cup S(b^{-1})</math> gelten auch die folgende Zerlegungen: <math>F_2=aS(a^{-1})\cup S(a)</math>, und <math>F_2=bS(b^{-1})\cup S(b)</math>,<br> | ||
| + | denn<br> | ||
| + | <math>aS(a^{-1}):=\{ax|x\in S(a^{-1}) \}=\{aa^{-1} \}\cup \{ax|x=a^{-1}g_0...,a\neq g_0\in E \}</math><br> | ||
| + | :::<math>=\{e \}\cup \{aa^{-1}g_0...|a\neq g_0\in E \}=\{e \}\cup S(b)\cup S(b^{-1})\cup S(a^{-1})</math><br> | ||
| + | und<br> | ||
| + | <math>bS(b^{-1}):=\{bx|x\in S(b^{-1}) \}=\{bb^{-1} \}\cup \{bx|x=b^{-1}g_0...,b\neq g_0\in E \}</math><br> | ||
| + | :::<math>=\{e \}\cup \{bb^{-1}g_0...|b\neq g_0\in E \}=\{e \}\cup S(a)\cup S(b^{-1})\cup S(a^{-1})</math>.<br> | ||
| + | Jetzt haben wir <math>F_2</math> paradox zerlegt. Dass heißt wir haben aus einer disjunkter Zerlegung zwei Kopien von der Gruppe erzeugt (bzw. der Menge an Wörtern). Dabei haben wir keine neue Wörter erzeugt sondern nur die bereits in den Teilmengen enthaltenen Wörter durch die Gruppenverknüpfgung modifiziert: von <math>S(a^{-1})</math> zu <math>aS(a^{-1})</math>. Jetzt benutzten wir diese Zerlegung für die Verdoppelung des Balles. | ||
| + | |||
| + | ==== Schritt III ==== | ||
| + | Dafür müssen wir eine Menge von Drehungen mit der <math>F_2</math> Gruppe identifizieren. Dafür ist es notwendig dass diese Menge unendlich viele Elemente besitzt, denn <math>F_2</math> besitzt auch unendlich viele Elementen. Die Gruppe der Drehungen um 120° ist somit kein gültiger Kandidat, denn sie enthält nur drei Elementen: nach einer dreifachen Drehung um 120° erreicht man die Ausgangsposition. Drehen wir um einen irrationalen Bruchteil von <math>\pi</math>, z. B. mit <math>\theta =\arccos \left({\tfrac {1}{3}}\right)</math>, und sei <math>a</math> eine entsprechende Drehung um die x-Achse, sowie <math>b</math> eine um die y-Achse, dann lässt sich zeigen, dass die dabei erzeugte Gruppe isomorph zu <math>F_2</math> ist. Wir nennen sie <math>H</math>. | ||
| + | |||
| + | ==== Schritt IV ==== | ||
| + | Dieser Schritt ist ein bisschen komplizierter also fassen wir am Anfang kurz zusammen: | ||
| + | # Wie haben eine Gruppe gefunden für welche eine paradoxe Zerlegung existiert. Das heißt die Elemente der Gruppen lassen sich in vier disjunkte Mengen zerlegen und aus diesen 4 Teilmengen lassen sich zwei Kopien der Ursprünglichen Menge konstruieren. Diese Gruppe heißt die freie Gruppe <math>F_2</math>. | ||
| + | # Wir haben eine Gruppe von Drehungen um die Achsen <math>x</math> und <math>y</math> gefunden, welche wir mit der Gruppe <math>F_2</math> identifizieren können, dass heißt die beiden Gruppen sind isomorph. Sie sind also von derselben Form und besitzen dieselben Eigenschaften. Insbesondere die paradoxe Zerlegung. Diese Gruppen von Drehungen haben wir <math>H</math> genannt. | ||
| + | |||
| + | Jetzt zerlegen wir den Einheitsball in zwei Kopien mit demselben Volumen! | ||
| + | |||
| + | Drehungen sind Operationen auf Punkten im Raum, also wir können die Drehungen aus <math>H</math> auf Punkten des Einheitsballes anwenden. Wie fangen aber zuerst mit der Einheitssphäre <math>S^2</math> an. Wir wenden <math>H</math> (also alle mögliche Drehungen aus <math>H</math>) auf jeden Punkt in <math>S^2</math> an. Um sich das besser vorstellen zu können betrachten wir zuerst einen einzelnen Punkt <math>m</math> an. Wenn <math>S^2</math> ein Globus wäre und wir einen Finger auf <math>m</math> setzten, dann würde unser Finger nach einer Drehung über einem anderen Punkt liegen. Sei <math>m</math> Deutschland, dann liegt unser Finger über Frankreich nach einer kleinen Drehung von dem Globus in Richtung Osten. | ||
| + | Die Menge aller Punkten die vom Ausgangspunkt <math>m</math> über alle erdenklichen Drehungen aus <math>H</math> erreichbar sind nennen wir die Bahn von <math>m</math>, sie sieht wie eine kugelförmige Staubwolke von gestreuten Punkten aus. Die Menge aller Bahnen von H auf <math>S^2</math> ist eine Partition von <math>S^2</math>. Alle Bahnen sind paarweise disjunkt und ihre Vereinigung ergibt <math>S^2</math> selbst. Das Auswahlaxiom erlaubt uns, aus jeder Bahn einen Repräsentanten zu wählen, sei daher <math>M</math> die Menge dieser Repräsentanten. Mit diesen Repräsentanten und den Mengen <math>S(a), S(a^{-1}), S(b), S(b^{-1})</math> können wir folgende Mengen konstruieren:<br> | ||
| + | <math>S(a)M=\{gm|g\in S(a), m\in M \}</math>, analog für <math>S(b)</math>,... Hier ist wichtig zu sagen, dass die Mengen <math>S(a),...</math> jetzt statt abstrakten Wörter, Drehungen um die <math>x</math> bzw. <math>y</math> Achse repräsentieren.<br> | ||
| + | |||
| + | Jetzt haben wir erfolgreich die Punkten der Einheitssphäre mit Elementen einer Gruppe für welche eine paradoxe Zerlegung existiert verknüpft. An der Stelle reicht es, um die Sphäre zu zerlegen, einfach dieselbe Prozedur wir im Schritt II durchzuführen. Anstatt von den Wörtern haben wir jetzt Drehungen und die Punkten reisen sozusagen mit den Drehungen mit. Weil die Strunktur etwas komplexer ist brauchen wir fünf statt vier Teilmengen, um den Prozess genau einzusehen, gehen Sie [https://de.wikipedia.org/wiki/Banach-Tarski-Paradoxon#Beweisskizze hier]. Die Zerlegung der Sphäre liefert uns sofort die Zerlegung des Balles, wir müssen die einzelne Punkten bloß mit einem Strahl zum Ursprung verinden (für eine bessere Vorstellung schauen wir uns wieder den [https://funfacts.mathi.uni-heidelberg.de/index.php/Datei:Dandelion_(107276119).jpg Löwenzahn] an.).<br> | ||
| + | |||
| + | Es ergibt sich dann die Frage: Wie kann es sein, dass durch eine Rotation neue Punkte in einer Menge enstehen? Die Frage ist berechtigt, denn es ist ziemlich schwer (wenn überhaupt möglich) sich das vorzustellen ohne zu denken dass man irgendwie mogeln muss. Mathematisch gesehen ist es einfach, die neue Punkte sind eine Folge der elementaren Gruppentheorie und Mengenlehre. Man bezieht sich bloß auf die Axiomatik einer Gruppe. Uns fehlt aber (leider) eine fassbare Vorstellung. Denn an der Stelle fehlt der Realität die unendliche Feinheit bzw. Porosität der Mathematik die hier notwendig ist. Im Alltag gibt es keine wirklichen Punkten und Geraden, alles hat in der Realität eine Breite und kann nicht wirklich eindimensional oder gar ohne Dimesion sein. Trotzdem findet man Spuren dieser - bisher rein mathematischen Eigenschaften - in manchen Bereichen der Physik, z.Bs. in [https://funfacts.mathi.uni-heidelberg.de/index.php/Banach-Tarski-Paradox#Hadron_Physics_and_Transfinite_Set_Theory Hadron Physics]. | ||
| + | |||
| + | ===Anschauliches Beispiel=== | ||
| + | |||
| + | Das Paradoxon wirkt vor allem dadurch unintuitiv, da man ein Volumen in unabzählbar unendlich viele unendlich kleine Stücke teilt, damit das entstehende Volumen größer ist als das Ausgangsvolumen. Man kann sich dies so vorstellen, dass man sich auf einer Kugel ein Startpunkt (S) aussucht, von welchem man entweder nach oben (O), unten (U), links (L) oder rechts (R) um eine konstante Distanz wandert. Der erreichte Punkt wird dann durch die letzte ausgeführte Aktion markiert und man wählt erneut eine Richtung aus in die man um die selbe Distanz wandert, aber man darf nicht in die entgegengesetzte Richtung laufen. Beispielsweise darf man nicht nach rechts wandern wenn man zuletzt nach links gelaufen ist. Bei der richtigen Wahl der Wanderdistanz wird kein Punkt mehr als ein Mal erreicht. Wenn man unendlich oft weiter wandert, hat man ''abzählbar'' unendlich viele Punkte auf der Kugel markiert. Da aber eine Kugel ''unabzählbar'' unendlich viele Punkte auf der Oberfläche hat, gibt es noch unerreichte Stellen. Wenn man diesen Vorgang unendlich oft auf allen verbleibenden Punkten wiederholt, dann wurde die vollständige Oberfläche der Kugel mit S, O, U, L und R markiert. Wenn man die Punkte mit dem Mittelpunkt der Kugel verbindet, dann kann man sich jeden Punkt stattdessen als ein „Stiel“ vorstellen, die alle zusammen das gesamte Volumen der Kugel darstellen. | ||
| + | |||
| + | Man kann nun die Kugel in fünf unvollständige Teile trennen, wobei jedes Teil jeweils nur eine Gruppe von Markierungen beinhaltet und die jeweiligen Markierungen nun als Namen für diese Teile dienen. Wenn man jetzt zum Beispiel das L-Teil nimmt und einen Schritt nach rechts rotiert, dann entsprechen die Punkte auf diesem Teil allen Punkten, die vor der letzten Linksdrehung auf dem L-Teil vorhanden waren, da sich die letzten Linksdrehungen der Punkte durch die gesamte Rechtsdrehung des L-Teils eliminieren. Da man nach einem S-, O-, U- oder L-Punkt jeweils noch nach links drehen kann, würde die Eliminierung der letzten Wanderungen von allen Punkten des L-Teils bedeuten, dass das Teil nach der Rechtsdrehung mit den S-, O-, U- und L-Teilen identisch sein. Wenn man noch das R-Teil dort direkt einfügt, dann besteht das entstandene Objekt aus den selben Teilen wie die vollständige Kugel, also ist es auch die selbe Kugel wie vorher. Da wir aber noch das O- und U-Teil übrig haben, kann man die selbe Vorgehensweise mit diesen Teilen machen: Eine Drehung nach unten des O-Teils resultiert in ein S-, O-, L- und R-Teil, und das Einfügen des U-Teils resultiert in einer zweiter Kopie derselben Kugel. | ||
| + | |||
| + | == Implikationen des Paradoxons im echten Leben == | ||
| + | === Verschwindende Schokolade === | ||
| + | Ein Beispiel für eine "Anwendung" des Banach-Tarski-Paradoxons in der Realität ist das Phänomen der "verschwindenden" Schokolade, welches in multiplen Videos über Social Media verbreitet wurde. Ähnlich wie auch bei Banach-Tarski geht es um ein Objekt, welches in unterschiedliche Teile zerlegt wurde, so zusammen zu setzen, dass man wieder das ursprüngliche Objekt erhält, dabei jedoch eines der Teile weg gelassen werden kann. | ||
| + | |||
| + | Besteht eine Schokoladentafel zum Beispiel aus 4 mal 8 einzelnen Stückchen, so lässt sich die Tafel auf eine bestimmte Weise zerschneiden, sodass sie beim erneuten Zusammensetzen wieder die ursprünglichen 4 mal 8 Stückchen enthält. Eines der Stückchen ist jedoch beim Zusammensetzen übrig geblieben und doch scheint es so als hätte die Schokoladentafel immer noch ihre ursprüngliche Größe. | ||
| − | + | Realistisch ist die Schokoladentafel um genau das herausgeschnittene Stückchen kürzer, was bedeutet, dass nicht mehr alle Stückchen der Tafel die selbe Größe haben. | |
| − | == | + | === Hadron Physics and Transfinite Set Theory === |
| − | + | Hadronen sind in der Physik subatomare Teilchen, die durch starke Wechselwirkung zusammengehalten werden. Die bekanntesten sind Protonen und Neutronen, also die Bestandteile von Atomkernen. Die Hadron Physics and Transfinite Set Theorie, welche erstmals von B.W.Augenstein 1984 veröffentlicht wurde, basiert auf der Quark-Theorie. Laut dieser bestehen Hadronen aus sehr viel kleineren Quarks. Die mathematische Verbindung zwischen dem Banach-Tarski-Paradoxon und dieser Theorie der Quantenphysik stellen die nicht-abelschen Gruppen dar, welche in der Hadronenphysik und in paradoxen Zerlegungen eine essenzielle Rolle spielen. | |
| − | + | Das von uns gewählte Paradoxon beschreibt grob gesagt eine Kugel, welche sich in beispielsweise fünf Teile zerlegen lässt. Drei dieser Teile ergeben eine Kopie der ursprünglichen Kugel, die zwei restlichen Teile ergeben eine zweite Kopie. Die Kugel könnte nun als ein Hadron aufgefasst werden und die einzelnen Bruchstücke als Quarks. Zerfällt nun ein fünf-Quark Hadron in einzelne Quarks, so kann daraus theoretisch ein zwei-Quark Hadron und ein drei-Quark Hadron zusammen gesetzt werden. | |
| − | + | Bisher gibt es keine Experimente, die mit dieser Theorie unvereinbar wären. | |
| − | + | <math></math> | |
== Verwandte Paradoxen == | == Verwandte Paradoxen == | ||
=== In der Ebene === | === In der Ebene === | ||
| − | [https://en.wikipedia.org/wiki/John_von_Neumann John von Neumann] arbeitete an den Bedingungen unter welchen paradoxische Zerlegungen möglich sind. Des weiteren fand er eine Version des Paradoxons in der Ebene, welche [https://de.wikipedia.org/wiki/Affine_Abbildung affine Abbildungen] | + | [https://en.wikipedia.org/wiki/John_von_Neumann John von Neumann] arbeitete an den Bedingungen unter welchen paradoxische Zerlegungen möglich sind. Des weiteren fand er eine Version des Paradoxons in der Ebene, welche [https://de.wikipedia.org/wiki/Affine_Abbildung affine Abbildungen] anstatt den üblichen Kongruenzenabbildungen. Diese Abbildungen erlauben mehr Freiheit, denn die Abstände zwischen den einzelnen Punkpaaren müssen nicht erhalten werden. |
=== Unendlich viele Bälle === | === Unendlich viele Bälle === | ||
| Zeile 59: | Zeile 126: | ||
* https://de.wikipedia.org/wiki/Banach-Tarski-Paradoxon | * https://de.wikipedia.org/wiki/Banach-Tarski-Paradoxon | ||
<references /> | <references /> | ||
| + | *Augenstein, B. W. (1984), Hadron physics and transfinite set theory, International Journal of Theoretical Physics, 23(12), 1197–1205, doi:10.1007/bf02213427 | ||
Aktuelle Version vom 18. April 2021, 12:18 Uhr
Das Banach-Tarski-Paradoxon (eng. Banach-Tarski-Paradox) oder auch Satz von Banach und Tarski ist ein Satz aus der geometrische Mengenlehre, welcher die Grenzen des anschaulichen Volumenbegriffs deutlich macht. Sei eine Kugel in drei oder mehr Dimensionen gegeben, existiert nach dem Satz eine Zerlegung der Kugel in endlich viele disjunkte Teilmengen bzw. Teile, sodass sich aus den Teilen zwei Kugeln mit demselben Radius wie die ursprüngliche Kugel konstruieren lassen. Dadurch verdoppelt sich das Volumen unersichtlich (denn eine Kugel wurde in zwei genauso große zerteilt). Dieses Paradoxon veranschaulicht somit, dass das mathematische Modell des Raumes in der Mathematik die Realität nicht in allen Eigenschaften widerspiegelt.
Im Gegensatz zu vielen anderen Sätzen aus der Geometrie, ist der Banach-Tarski Satz ziemlich abhängig von der Wahl des angemessenen Axiomgesetzes. Das Axiom der Wahl (eng. Axiom of Choice) erlaubt für einen Beweis, da überabzählbar viele Wahlen getroffen werden müssen. Dies folgt aus der Natur der Teilmengen in welche man den Ball zerlegt, diese sind nämlich unendlich filigran bzw. staubwolkenartig (siehe Löwenzahn[1]). Eine andere Auswahl an Axiomen ergibt aber, dass eine solche Zerlegung und Rekonstruktion der Kugel nicht möglich sind.
Vorwissen
Hilberts Hotel
Hilberts Hotel (eng. Hilbert's Paradox of the Grand Hotel) ist ein Gedankenexperiment, erschaffen von David Hilbert und eingeführt in seiner Vorlesung "Über das Unendliche" im Jahre 1924. Es demonstriert die kontraintuitiven Eigenschaften des Unendlichen, wie z.B. die Eigenschaft, dass ein Hotel mit unendlichen Räumen und einem Gast pro Raum nicht voll besetzt ist und weitere Gäste problemlos einen Raum zugewiesen kriegen können. Die bei uns wichtigere Eigenschaft ist, dass, wenn ein Gast das Hotel verlässt, alle anderen Gäste so umgeschoben werden können, dass wieder jeder Raum besetzt ist und das Hotel scheinbar wieder vollgebucht ist.
Da Hilberts Hotel in der Vorlesung besprochen wurde und auch schon von einer anderen Gruppe behandelt wird, werden wir den Artikel Hilberts Hotel hier verlinken.
Hilberts Hotel kann auch auf Formen angewandt werden. Wenn man aus einem Kreis einen einzigen Punkt entfernt (siehe Bild[2]), entsteht scheinbar eine Lücke. Da aber der Umfang eines Kreises immer irrational ist (u = 2πr mit π irrational), kann man von der Lücke aus entlang dem Umfang Strecken von einer rationalen Länge (bsp. Länge r) abmessen und den entsprechenden Punkt markieren (den ersten mit 1, den zweiten mit 2 etc.). Am Ende des Prozesses hat man unendlich viele Punkte markiert, mit denen man entsprechend Hilberts Hotel die Lücke einfüllen kann: Punkt 1 füllt die Lücke, Punkt 2 füllt die Lücke, die durch Punkt 1 entstanden ist und so weiter. Somit ist also Hilberts Hotel auch anwendbar auf Formen und Körper.
Hyperwebster
Der Hyperwebster[3] ist eine Erfindung von Dr. Ian Steward, um zu veranschaulichen, wie groß unzählbare Unendlichkeit sein kann.
Der Hyperwebster ist eine Version von Webster's Dictionary[4], wo jede mögliche Buchstabenkombination vorkommen soll. Man starte mit dem Buchstaben A, dann AA, dann AAA, und so weiter bis man unendlich viele A's hat. Danach kommt AB, ABA, ABAA, ABAAA, ..., AC, ..., AZ, ..., B, BA, BAA, ..., Z, ZA, ZAA etc. Am Ende sieht der Hyperwebster dann ungefähr so aus:
A, AA, AAA, AAAA, ..., AB, ABA, ABAA, .... AAB, AABA, ..., AC, ... AZ, AZAA, ...
B, BA, BAA, ..., BB, BBA, ..., BZ, BZA, ...
...
Z, ZA, ZAA, ..., ZB, ZBA, ..., ZZZZZZZZZZZZZZZ...
Nun haben wir ein Wörterbuch, welches jedes mögliche Wort, jeden möglichen Satz, jede mögliche Buchstabenkombination enthält. Der Verlag möchte jetzt dieses Wörterbuch ausdrucken, es wäre aber viel zu groß. Der Verlag fasst also alle Wörter in 26 Bände zusammen, somit werden alle Wörter mit einem bestimmten Anfangsbuchstaben in einen Band gepackt.
Um jetzt Platz zu sparen, nimmt der Verlag jeden Band und streicht den Anfangsbuchstaben jedes Wortes, da jeder Anfangsbuchstabe nur ein Mal pro Band vorkommt. Dabei stellt sich heraus, wenn man den Anfangsbuchstaben jedes Bandes kürzt, man wieder den Hyperwebster selbst erhält. Der Hyperwebster ist also in diesem Sinne ein sich selbst enthaltendes (selbstähnliches) Fraktal, da man durch die oben beschriebene Methode aus einem Hyperwebster gleich 26 machen kann.
Paradox
Der Banach-Tarski Satz widerspricht der gängingen geometrischen Intuition und wird somit oft auch Banach-Tarski Paradoxon genannt. Nach Banach-Tarski wird ein Ball in zwei weitere Bälle mit demselben Volumen zerlegt ohne den Ball zu dehnen, biegen oder neue Punkte dem Ball hinzuzufügen. Tatsächlich werden die Teile, in welche der Ball zerlegt wird, nur rotiert und geschoben (entspricht einer Translation in der Mathematik). Es scheint unmöglich zu sein, durch diese Operationen das Volumen zu erhöhen, da sie, intuitiv betrachtet, das Volumen erhalten. Mathematisch ist es auch so, nur kann man dieselbe Intuition bei dieser Zerlegung des Balles nicht anwenden da für die Teile in welche der Ball zerlegt wird, kein Volumen definiert werden kann.

Nach dem Widerzusammenfügen der Teile lässt sich wieder ein Volumen definieren und nun ist es so, dass das Volumen anders als das ursprüngliche Volumen ist (nämlich doppelt so groß). In der Realität lassen sich solche Umformungen leider nicht durchführen da der Ball in unendlich feine bzw. dünne Teile zerlegt werden müsste.
Eine allgemeinere Version des Satzes existiert, oft informell "pea and the Sun paradox" (dt. Das Erbse-Sonne Paradoxon) genannt. Diese besagt, dass eine Erbse in Stücke zerlegt werden kann und dass sich aus den entstehenden Stücken dann die Sonne konstruieren lässt[5].
Konsequenzen
Die wichtigste Konsequenz des Paradoxons von Banach und Tarski besteht in der Einsicht, dass nicht allen Teilmengen von [math]\mathbb{R}^3[/math] sinnvoll ein Volumen zugewiesen werden kann[6]. Wobei unter sinnvoll das Erfüllen von manchen Eigenschaften, wie zum Beispiel die Bewegungsinvarianz, zu verstehen ist. Dies folgt aus Banach-Tarski, denn während der Zerlegung des Balles entstehen Teilmengen von [math]\mathbb{R}^3[/math], welche wie eine kugelförmige Punktwolke aussehen, wobei alle Punkten mit einem Strahl zum Mittelpunkt verbunden sind. Teilmengen dieser Form lässt sich kein Volumen widerspruchsfrei zuordnen[7].
Geschichte, Satz von Banach und Tarski
In einem in 1924 veröffentlichten Paper gaben Stefan Banach und Alfred Tarski eine Konstruktion einer solchen paradoxischen Zerlegung, gegründet in der früheren Arbeit von Giuseppe Vitali. Banach und Tarski haben den folgenden, allgemeineren (auch stärkeren) Satz bewiesen:
- Satz: Sei [math]d \ge 3[/math] eine ganze Zahl und seien [math]X, Y\subset \mathbb{R}^d[/math] beschränkte Mengen mit nicht-leerem Inneren. Dann gibt es eine natürliche Zahl [math]n[/math] und eine disjunkte Zerlegung [math]X_1, \dots, X_n[/math] von [math]X[/math] und zugehörige Bewegung [math]\beta_1, \dots, \beta_n[/math] derart, dass [math]Y[/math] die disjunkte Vereinigung der Mengen [math]\beta_1(X_1), \dots, \beta_n(X_n)[/math] ist.
Das heißt, dass in [math]\mathbb{R}^d:d\geq 3[/math] eine beschränkte Menge mit nicht-leerem Inneren sich disjunkt zerlegen und dann in eine beliebige, beschränkte Menge mit nicht-leerem Inneren wieder disjunkt vereinigen lassen kann. Da wir die durch die Zerlegung konstruierte Teilmengen nur bewegen, werden keine neue Punkten erzeugt und die Abstände zwischen allen Punkten eines [math]X_j[/math]werden paarweise erhalten. Somit folgt das Banach-Tarski-Paradoxon als ein bestimmter Fall: Sei die Menge [math]X[/math] von oben ein Ball und die Menge [math]Y[/math] zwei Kopien des Balles mit demselben Radius wie der Ball [math]X[/math]. Dann gilt: [math]X,Y\subset \mathbb{R^3}[/math], da Bälle per Definition beschränkt sind und ein nichtleeres Innere haben. Nach dem Satz gilt, dass eine disjunkte Zerlegung [math]X_1,..., X_n[/math] von [math]X[/math] zusammen mit der zugehörigen Bewegung [math]\beta _1,..., \beta _n[/math] existiert, sodass [math]Y=\beta _1(X_1)\dot\cup \beta _2(X_2)\ \dot\cup ... \dot\cup\ \beta _n(X_n)[/math] gilt.
Der allgemeinere Satz von Banach und Tarski gilt in einer und zwei Dimensionen nicht, da die Bewegungsfreiheit in diesen Dimensionen zu beschränkt ist. Als Folge dessen besitzen alle Figuren, welche durch eine Zerlegung und eine zugehörige Bewegung der Teile, sich ineinander umformen lassen, denselben Flächeninhalt. Banach und Tarski haben aber gezeigt, dass, wenn Zerlegungen in abzählbar viele Teile (statt endlich viele) erlaubt sind, die analoge Version des Satzes immer noch gilt.
Beweisskizze
Anmerkung: hier erklären wir bloß die Grundzüge des Beweises, eine ausführlichere Beweisskizze finden Sie hier.
Der Beweis benutzt die Tatsache, dass Drehungen im Raum mathematisch als Elemente einer Gruppe aufgefasst werden können. Somit kann man sie miteinander verknüpfen und auf andere Objekte anwenden, wobei die Bedingungen der Gruppe erfüllt sind:
- Die Verknüpfung mehrerer Drehungen ist wiederum eine Drehung.
- Die Verknüpfungsoperation ist assoziativ.
- In einer Verknüpfungskette [math] g_1\dots\ g_i g_i^{-1}\dots\ g_n [/math] eliminieren sich die benachbarten Elemente [math] g_{i} [/math] und [math] g_{i}^{-1} [/math], da sie zueinander invers sind. Dies gilt für Drehungen ebenso. Drehungen operieren auf Punkten oder Punktmengen im Raum, indem sie deren Lage verändern.
Für den Beweis wird eine ganz besondere Gruppe betrachtet; Die freie Gruppe [math]F_2[/math] mit ihren Erzeugern [math]a[/math] und [math]b[/math] besteht abstrakt definiert aus Wörtern über dem Alphabet (Alphabete sind Mengen von Buchstaben) [math]E:=\{a,a^{-1},b,b^{-1}\}[/math], in denen keine Elemente zu deren Inversen benachbart sind. Die Verknüpfung der Gruppe stellt die Konkatenation dar, wobei möglicherweise entstandene Invers-Paare iterativ entfernt werden, bis keine solchen Paare im verknüpften Wort mehr vorkommen. Das leere Wort [math]\varepsilon[/math] stellt das neutrale Element der Gruppe dar. Die Darstellung jedes Elements von [math]F_2[/math] als gekürztes Wort ist dabei eindeutig.
Schritt I
Wir definieren die Mengen [math]S(a), S(b), S(a^{-1}), S(b^{-1})[/math]. Hier ist [math]S(a)[/math] die Menge aller Wörter aus [math]F_2[/math], die links mit [math]a[/math] beginnen, z.B.:[math]ab, abb,aba^{-1}[/math]. Die anderen S-Mengen sind analog definiert. Wir fordern wir oben dass die Darstellung der Wörter gekürzt ist, also [math]a[/math] und [math]a^{-1}[/math] kommen nicht nebeneinander vor.
Schritt II
Wie zeigen dass eine paradoxe Zerlegung von [math]F_2[/math] existiert.
Neben der üblichen Zerlegung: [math]F_2={e}\cup S(a)\cup S(a^{-1})\cup S(b)\cup S(b^{-1})[/math] gelten auch die folgende Zerlegungen: [math]F_2=aS(a^{-1})\cup S(a)[/math], und [math]F_2=bS(b^{-1})\cup S(b)[/math],
denn
[math]aS(a^{-1}):=\{ax|x\in S(a^{-1}) \}=\{aa^{-1} \}\cup \{ax|x=a^{-1}g_0...,a\neq g_0\in E \}[/math]
- [math]=\{e \}\cup \{aa^{-1}g_0...|a\neq g_0\in E \}=\{e \}\cup S(b)\cup S(b^{-1})\cup S(a^{-1})[/math]
- [math]=\{e \}\cup \{aa^{-1}g_0...|a\neq g_0\in E \}=\{e \}\cup S(b)\cup S(b^{-1})\cup S(a^{-1})[/math]
und
[math]bS(b^{-1}):=\{bx|x\in S(b^{-1}) \}=\{bb^{-1} \}\cup \{bx|x=b^{-1}g_0...,b\neq g_0\in E \}[/math]
- [math]=\{e \}\cup \{bb^{-1}g_0...|b\neq g_0\in E \}=\{e \}\cup S(a)\cup S(b^{-1})\cup S(a^{-1})[/math].
- [math]=\{e \}\cup \{bb^{-1}g_0...|b\neq g_0\in E \}=\{e \}\cup S(a)\cup S(b^{-1})\cup S(a^{-1})[/math].
Jetzt haben wir [math]F_2[/math] paradox zerlegt. Dass heißt wir haben aus einer disjunkter Zerlegung zwei Kopien von der Gruppe erzeugt (bzw. der Menge an Wörtern). Dabei haben wir keine neue Wörter erzeugt sondern nur die bereits in den Teilmengen enthaltenen Wörter durch die Gruppenverknüpfgung modifiziert: von [math]S(a^{-1})[/math] zu [math]aS(a^{-1})[/math]. Jetzt benutzten wir diese Zerlegung für die Verdoppelung des Balles.
Schritt III
Dafür müssen wir eine Menge von Drehungen mit der [math]F_2[/math] Gruppe identifizieren. Dafür ist es notwendig dass diese Menge unendlich viele Elemente besitzt, denn [math]F_2[/math] besitzt auch unendlich viele Elementen. Die Gruppe der Drehungen um 120° ist somit kein gültiger Kandidat, denn sie enthält nur drei Elementen: nach einer dreifachen Drehung um 120° erreicht man die Ausgangsposition. Drehen wir um einen irrationalen Bruchteil von [math]\pi[/math], z. B. mit [math]\theta =\arccos \left({\tfrac {1}{3}}\right)[/math], und sei [math]a[/math] eine entsprechende Drehung um die x-Achse, sowie [math]b[/math] eine um die y-Achse, dann lässt sich zeigen, dass die dabei erzeugte Gruppe isomorph zu [math]F_2[/math] ist. Wir nennen sie [math]H[/math].
Schritt IV
Dieser Schritt ist ein bisschen komplizierter also fassen wir am Anfang kurz zusammen:
- Wie haben eine Gruppe gefunden für welche eine paradoxe Zerlegung existiert. Das heißt die Elemente der Gruppen lassen sich in vier disjunkte Mengen zerlegen und aus diesen 4 Teilmengen lassen sich zwei Kopien der Ursprünglichen Menge konstruieren. Diese Gruppe heißt die freie Gruppe [math]F_2[/math].
- Wir haben eine Gruppe von Drehungen um die Achsen [math]x[/math] und [math]y[/math] gefunden, welche wir mit der Gruppe [math]F_2[/math] identifizieren können, dass heißt die beiden Gruppen sind isomorph. Sie sind also von derselben Form und besitzen dieselben Eigenschaften. Insbesondere die paradoxe Zerlegung. Diese Gruppen von Drehungen haben wir [math]H[/math] genannt.
Jetzt zerlegen wir den Einheitsball in zwei Kopien mit demselben Volumen!
Drehungen sind Operationen auf Punkten im Raum, also wir können die Drehungen aus [math]H[/math] auf Punkten des Einheitsballes anwenden. Wie fangen aber zuerst mit der Einheitssphäre [math]S^2[/math] an. Wir wenden [math]H[/math] (also alle mögliche Drehungen aus [math]H[/math]) auf jeden Punkt in [math]S^2[/math] an. Um sich das besser vorstellen zu können betrachten wir zuerst einen einzelnen Punkt [math]m[/math] an. Wenn [math]S^2[/math] ein Globus wäre und wir einen Finger auf [math]m[/math] setzten, dann würde unser Finger nach einer Drehung über einem anderen Punkt liegen. Sei [math]m[/math] Deutschland, dann liegt unser Finger über Frankreich nach einer kleinen Drehung von dem Globus in Richtung Osten.
Die Menge aller Punkten die vom Ausgangspunkt [math]m[/math] über alle erdenklichen Drehungen aus [math]H[/math] erreichbar sind nennen wir die Bahn von [math]m[/math], sie sieht wie eine kugelförmige Staubwolke von gestreuten Punkten aus. Die Menge aller Bahnen von H auf [math]S^2[/math] ist eine Partition von [math]S^2[/math]. Alle Bahnen sind paarweise disjunkt und ihre Vereinigung ergibt [math]S^2[/math] selbst. Das Auswahlaxiom erlaubt uns, aus jeder Bahn einen Repräsentanten zu wählen, sei daher [math]M[/math] die Menge dieser Repräsentanten. Mit diesen Repräsentanten und den Mengen [math]S(a), S(a^{-1}), S(b), S(b^{-1})[/math] können wir folgende Mengen konstruieren:
[math]S(a)M=\{gm|g\in S(a), m\in M \}[/math], analog für [math]S(b)[/math],... Hier ist wichtig zu sagen, dass die Mengen [math]S(a),...[/math] jetzt statt abstrakten Wörter, Drehungen um die [math]x[/math] bzw. [math]y[/math] Achse repräsentieren.
Jetzt haben wir erfolgreich die Punkten der Einheitssphäre mit Elementen einer Gruppe für welche eine paradoxe Zerlegung existiert verknüpft. An der Stelle reicht es, um die Sphäre zu zerlegen, einfach dieselbe Prozedur wir im Schritt II durchzuführen. Anstatt von den Wörtern haben wir jetzt Drehungen und die Punkten reisen sozusagen mit den Drehungen mit. Weil die Strunktur etwas komplexer ist brauchen wir fünf statt vier Teilmengen, um den Prozess genau einzusehen, gehen Sie hier. Die Zerlegung der Sphäre liefert uns sofort die Zerlegung des Balles, wir müssen die einzelne Punkten bloß mit einem Strahl zum Ursprung verinden (für eine bessere Vorstellung schauen wir uns wieder den Löwenzahn an.).
Es ergibt sich dann die Frage: Wie kann es sein, dass durch eine Rotation neue Punkte in einer Menge enstehen? Die Frage ist berechtigt, denn es ist ziemlich schwer (wenn überhaupt möglich) sich das vorzustellen ohne zu denken dass man irgendwie mogeln muss. Mathematisch gesehen ist es einfach, die neue Punkte sind eine Folge der elementaren Gruppentheorie und Mengenlehre. Man bezieht sich bloß auf die Axiomatik einer Gruppe. Uns fehlt aber (leider) eine fassbare Vorstellung. Denn an der Stelle fehlt der Realität die unendliche Feinheit bzw. Porosität der Mathematik die hier notwendig ist. Im Alltag gibt es keine wirklichen Punkten und Geraden, alles hat in der Realität eine Breite und kann nicht wirklich eindimensional oder gar ohne Dimesion sein. Trotzdem findet man Spuren dieser - bisher rein mathematischen Eigenschaften - in manchen Bereichen der Physik, z.Bs. in Hadron Physics.
Anschauliches Beispiel
Das Paradoxon wirkt vor allem dadurch unintuitiv, da man ein Volumen in unabzählbar unendlich viele unendlich kleine Stücke teilt, damit das entstehende Volumen größer ist als das Ausgangsvolumen. Man kann sich dies so vorstellen, dass man sich auf einer Kugel ein Startpunkt (S) aussucht, von welchem man entweder nach oben (O), unten (U), links (L) oder rechts (R) um eine konstante Distanz wandert. Der erreichte Punkt wird dann durch die letzte ausgeführte Aktion markiert und man wählt erneut eine Richtung aus in die man um die selbe Distanz wandert, aber man darf nicht in die entgegengesetzte Richtung laufen. Beispielsweise darf man nicht nach rechts wandern wenn man zuletzt nach links gelaufen ist. Bei der richtigen Wahl der Wanderdistanz wird kein Punkt mehr als ein Mal erreicht. Wenn man unendlich oft weiter wandert, hat man abzählbar unendlich viele Punkte auf der Kugel markiert. Da aber eine Kugel unabzählbar unendlich viele Punkte auf der Oberfläche hat, gibt es noch unerreichte Stellen. Wenn man diesen Vorgang unendlich oft auf allen verbleibenden Punkten wiederholt, dann wurde die vollständige Oberfläche der Kugel mit S, O, U, L und R markiert. Wenn man die Punkte mit dem Mittelpunkt der Kugel verbindet, dann kann man sich jeden Punkt stattdessen als ein „Stiel“ vorstellen, die alle zusammen das gesamte Volumen der Kugel darstellen.
Man kann nun die Kugel in fünf unvollständige Teile trennen, wobei jedes Teil jeweils nur eine Gruppe von Markierungen beinhaltet und die jeweiligen Markierungen nun als Namen für diese Teile dienen. Wenn man jetzt zum Beispiel das L-Teil nimmt und einen Schritt nach rechts rotiert, dann entsprechen die Punkte auf diesem Teil allen Punkten, die vor der letzten Linksdrehung auf dem L-Teil vorhanden waren, da sich die letzten Linksdrehungen der Punkte durch die gesamte Rechtsdrehung des L-Teils eliminieren. Da man nach einem S-, O-, U- oder L-Punkt jeweils noch nach links drehen kann, würde die Eliminierung der letzten Wanderungen von allen Punkten des L-Teils bedeuten, dass das Teil nach der Rechtsdrehung mit den S-, O-, U- und L-Teilen identisch sein. Wenn man noch das R-Teil dort direkt einfügt, dann besteht das entstandene Objekt aus den selben Teilen wie die vollständige Kugel, also ist es auch die selbe Kugel wie vorher. Da wir aber noch das O- und U-Teil übrig haben, kann man die selbe Vorgehensweise mit diesen Teilen machen: Eine Drehung nach unten des O-Teils resultiert in ein S-, O-, L- und R-Teil, und das Einfügen des U-Teils resultiert in einer zweiter Kopie derselben Kugel.
Implikationen des Paradoxons im echten Leben
Verschwindende Schokolade
Ein Beispiel für eine "Anwendung" des Banach-Tarski-Paradoxons in der Realität ist das Phänomen der "verschwindenden" Schokolade, welches in multiplen Videos über Social Media verbreitet wurde. Ähnlich wie auch bei Banach-Tarski geht es um ein Objekt, welches in unterschiedliche Teile zerlegt wurde, so zusammen zu setzen, dass man wieder das ursprüngliche Objekt erhält, dabei jedoch eines der Teile weg gelassen werden kann.
Besteht eine Schokoladentafel zum Beispiel aus 4 mal 8 einzelnen Stückchen, so lässt sich die Tafel auf eine bestimmte Weise zerschneiden, sodass sie beim erneuten Zusammensetzen wieder die ursprünglichen 4 mal 8 Stückchen enthält. Eines der Stückchen ist jedoch beim Zusammensetzen übrig geblieben und doch scheint es so als hätte die Schokoladentafel immer noch ihre ursprüngliche Größe.
Realistisch ist die Schokoladentafel um genau das herausgeschnittene Stückchen kürzer, was bedeutet, dass nicht mehr alle Stückchen der Tafel die selbe Größe haben.
Hadron Physics and Transfinite Set Theory
Hadronen sind in der Physik subatomare Teilchen, die durch starke Wechselwirkung zusammengehalten werden. Die bekanntesten sind Protonen und Neutronen, also die Bestandteile von Atomkernen. Die Hadron Physics and Transfinite Set Theorie, welche erstmals von B.W.Augenstein 1984 veröffentlicht wurde, basiert auf der Quark-Theorie. Laut dieser bestehen Hadronen aus sehr viel kleineren Quarks. Die mathematische Verbindung zwischen dem Banach-Tarski-Paradoxon und dieser Theorie der Quantenphysik stellen die nicht-abelschen Gruppen dar, welche in der Hadronenphysik und in paradoxen Zerlegungen eine essenzielle Rolle spielen.
Das von uns gewählte Paradoxon beschreibt grob gesagt eine Kugel, welche sich in beispielsweise fünf Teile zerlegen lässt. Drei dieser Teile ergeben eine Kopie der ursprünglichen Kugel, die zwei restlichen Teile ergeben eine zweite Kopie. Die Kugel könnte nun als ein Hadron aufgefasst werden und die einzelnen Bruchstücke als Quarks. Zerfällt nun ein fünf-Quark Hadron in einzelne Quarks, so kann daraus theoretisch ein zwei-Quark Hadron und ein drei-Quark Hadron zusammen gesetzt werden.
Bisher gibt es keine Experimente, die mit dieser Theorie unvereinbar wären.
[math][/math]
Verwandte Paradoxen
In der Ebene
John von Neumann arbeitete an den Bedingungen unter welchen paradoxische Zerlegungen möglich sind. Des weiteren fand er eine Version des Paradoxons in der Ebene, welche affine Abbildungen anstatt den üblichen Kongruenzenabbildungen. Diese Abbildungen erlauben mehr Freiheit, denn die Abstände zwischen den einzelnen Punkpaaren müssen nicht erhalten werden.
Unendlich viele Bälle
Ähnlich zu dem "pea and the Sun paradox" folgt aus der stärkeren Version des Satztes dass man einen Ball in undendlich viele Kopien von sich selbst umformen kann. Indem man wieder die Teile aus der Zerlegung bloß bewegt. Der Fall mit unendlich vielen Bällen lässt sich aber auch mithilfe von dem Banach-Tarski Paradoxon beweisen[8] (der Spezialfall mir einem Ball und seiner Kopie).
- Siehe auch Hilberts Hotel und Hyperwebster!
Quellen
- https://www.youtube.com/watch?v=s86-Z-CbaHA&t=500s&ab_channel=Vsauce
- https://en.wikipedia.org/wiki/Banach%E2%80%93Tarski_paradox#Obtaining_infinitely_many_balls_from_one
- https://de.wikipedia.org/wiki/Banach-Tarski-Paradoxon
- ↑ https://funfacts.mathi.uni-heidelberg.de/index.php/Datei:Dandelion_(107276119).jpg
- ↑ https://funfacts.mathi.uni-heidelberg.de/index.php/Datei:Circle_graphic_updated_3.jpg
- ↑ https://www.latg.org/blog/2018/06/09/hyperwebster/
- ↑ https://en.wikipedia.org/wiki/Webster%27s_Dictionary
- ↑ https://plus.maths.org/content/pea-and-sun
- ↑ https://dmg.tuwien.ac.at/winkler/pub/bantar.pdf
- ↑ https://dmg.tuwien.ac.at/winkler/pub/bantar.pdf
- ↑ https://en.wikipedia.org/wiki/Banach%E2%80%93Tarski_paradox#Obtaining_infinitely_many_balls_from_one
- Augenstein, B. W. (1984), Hadron physics and transfinite set theory, International Journal of Theoretical Physics, 23(12), 1197–1205, doi:10.1007/bf02213427