Basler Problem: Unterschied zwischen den Versionen
K (Links hinzufügen) |
|||
| (Eine dazwischenliegende Version von einem anderen Benutzer wird nicht angezeigt) | |||
| Zeile 110: | Zeile 110: | ||
=== Formaler Beweis (2) === | === Formaler Beweis (2) === | ||
| − | Als Zusatz geben wir noch einen weiteren interessanten Beweis an, der auf <span style="font-variant:small-caps;">Fourier</span>-Analysis beruht. Hierbei benötigen wir als Schlüssel die [https://de.wikipedia.org/wiki/Parsevalsche_Gleichung <span style="font-variant:small-caps;">Parseval</span>'sche Identität] | + | Als Zusatz geben wir noch einen weiteren interessanten Beweis an, der auf <span style="font-variant:small-caps;">Fourier</span>-Analysis beruht. Hierbei benötigen wir als Schlüssel die [https://de.wikipedia.org/wiki/Parsevalsche_Gleichung <span style="font-variant:small-caps;">Parseval</span>'sche Identität]<ref name="WikiParseval" />, die wir wieder ohne Beweis verwenden möchten. Diese erlaubt es, ähnlich wie in Beweis <math>(1)</math>, die Reihe <math>\sum_{n=1}^{\infty}\frac{1}{n^2}</math> auf die Berechnung eines (sehr leichten!) Integrals zurückzuführen. Ansonsten benötigen wir noch ein paar elementare Resultate der <span style="font-variant:small-caps;">Fourier</span>-Analysis sowie solche der komplexen Analysis. |
<!-- \begin{proof} --> | <!-- \begin{proof} --> | ||
| Zeile 121: | Zeile 121: | ||
c_n \;\; = \;\; \frac{1}{2\pi} \cdot \int_{-\pi}^{\pi} f(x) \cdot \mathrm{e}^{-\mathrm{i}nx} \, dx \qquad \forall n \in \mathbb{Z}. | c_n \;\; = \;\; \frac{1}{2\pi} \cdot \int_{-\pi}^{\pi} f(x) \cdot \mathrm{e}^{-\mathrm{i}nx} \, dx \qquad \forall n \in \mathbb{Z}. | ||
</math> | </math> | ||
| − | Wir setzen <math>f(x) := x \; (x \in \mathbb{R})</math> und berechnen mithilfe der [https://de.wikipedia.org/wiki/Eulersche_Formel | + | Wir setzen <math>f(x) := x \; (x \in \mathbb{R})</math> und berechnen mithilfe der [https://de.wikipedia.org/wiki/Eulersche_Formel Eulerformel] <math>\mathrm{e}^{\mathrm{i}z} = \cos(z) + \mathrm{i} \cdot \sin(z) \; (z \in \mathbb{C})</math> zunächst die Fourierkoeffizienten: |
:<math>\displaystyle | :<math>\displaystyle | ||
\begin{align} | \begin{align} | ||
c_n \;\; &= \;\; \frac{1}{2\pi} \cdot \int_{-\pi}^{\pi} x \cdot \mathrm{e}^{-\mathrm{i}nx} \, dx \;\; \overset{\text{part.}}{\underset{\text{Int.}}{=}} \;\; \frac{1}{2\pi} \left( \left[\frac{\mathrm{i}}{n} \cdot x \cdot \mathrm{e}^{-\mathrm{i}nx}\right]_{-\pi}^{\pi} \;\; - \int_{-\pi}^{\pi} \frac{\mathrm{i}}{n} \cdot \mathrm{e}^{-\mathrm{i}nx} \, dx \right) \\ | c_n \;\; &= \;\; \frac{1}{2\pi} \cdot \int_{-\pi}^{\pi} x \cdot \mathrm{e}^{-\mathrm{i}nx} \, dx \;\; \overset{\text{part.}}{\underset{\text{Int.}}{=}} \;\; \frac{1}{2\pi} \left( \left[\frac{\mathrm{i}}{n} \cdot x \cdot \mathrm{e}^{-\mathrm{i}nx}\right]_{-\pi}^{\pi} \;\; - \int_{-\pi}^{\pi} \frac{\mathrm{i}}{n} \cdot \mathrm{e}^{-\mathrm{i}nx} \, dx \right) \\ | ||
| − | &= \;\; \frac{\mathrm{1}}{2\pi} \left( \frac{\mathrm{i}}{n} \left( \pi \mathrm{e}^{-\mathrm{i}n\pi} + \pi \mathrm{e}^{\mathrm{i}n\pi} \right) + \frac{1}{n^2} \left( \mathrm{e}^{-\mathrm{i}n\pi} - \mathrm{e}^{\mathrm{i}n\pi} \right) \right) \;\; \overset{\text{Euler-}}{\underset{\text{ | + | &= \;\; \frac{\mathrm{1}}{2\pi} \left( \frac{\mathrm{i}}{n} \left( \pi \mathrm{e}^{-\mathrm{i}n\pi} + \pi \mathrm{e}^{\mathrm{i}n\pi} \right) + \frac{1}{n^2} \left( \mathrm{e}^{-\mathrm{i}n\pi} - \mathrm{e}^{\mathrm{i}n\pi} \right) \right) \;\; \overset{\text{Euler-}}{\underset{\text{formel}}{=}} \;\; \frac{\mathrm{1}}{2\pi} \left( \frac{2\pi\mathrm{i}}{n}\cos(n\pi) - \frac{2\mathrm{i}}{n^2}\sin(n\pi) \right) \;\; \\ |
&= \;\; \frac{n\pi\cos(n\pi) - \sin(n\pi)}{\pi n^2}\mathrm{i} \;\; = \;\; \frac{\cos(n\pi)}{n}\mathrm{i} \;\; = \;\; \frac{(-1)^n}{n}\mathrm{i} \qquad \forall n \in \mathbb{Z} \setminus \{0\} | &= \;\; \frac{n\pi\cos(n\pi) - \sin(n\pi)}{\pi n^2}\mathrm{i} \;\; = \;\; \frac{\cos(n\pi)}{n}\mathrm{i} \;\; = \;\; \frac{(-1)^n}{n}\mathrm{i} \qquad \forall n \in \mathbb{Z} \setminus \{0\} | ||
\end{align} | \end{align} | ||
Aktuelle Version vom 15. April 2021, 15:13 Uhr
Das Basler Problem ist die Frage nach dem Wert der Summe der Kehrwerte der Quadratzahlen, also dem Wert der Reihe
- [math]\displaystyle \sum_{n = 1}^{\infty} \frac{1}{n^2} \;\; = \;\; \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots. [/math]
Geschichte
Im Jahr 1644 stellte Pietro Mengoli (1626-1686, italienischer Mathematiker) die Frage nach dem Wert der Summe der Kehrwerte der Quadratzahlen. Nach einigen erfolglosen Lösungsversuchen anderer Mathematiker, wie John Wallis, Jakob I und Johann Bernoulli und Gottfried Wilhelm Leibniz löste 1735, 91 Jahre später, Leonhard Euler (1707-1783, Schweizer Mathematiker) das Problem und zeigte, dass der Wert der Reihe [math]\frac{\pi^2}{6}[/math] beträgt. Das Problem ist nach Eulers Heimatstadt Basel benannt, in welcher auch die Bernoulli Familie lebte.[1][2]
Beweise
Ziel dieses Abschnitts ist es, verschiedene Beweise der folgenden Identität zu liefern:
- [math]\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^2} \;\; = \;\; \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \dots = \frac{\pi^2}{6} [/math]
Dabei wollen wir zunächst die historisch erste Lösung von Leonhard Euler präsentieren und anschließend zwei weitere (mehr oder weniger streng) formale Beweise angeben, die allerdings erst deutlich später gefunden wurden.
Eulers erste Lösung (1735)
Die Idee der ersten Lösung von Euler beruht auf der bekannten Taylorentwicklung der Sinusfunktion einerseits und deren Darstellung als unendliches Produkt andererseits.[3] Die rigorose Rechtfertigung für diese Argumentation lieferte Karl Weierstraß erst etwa 100 Jahre später. Einerseits ist die Taylorentwicklung der Sinusfunktion um den Entwicklungspunkt [math]0[/math] gegeben durch
- [math]\displaystyle \sin(x) \;\; = \;\; \sum_{n=0}^{\infty} (-1)^n \frac{x^{2n+1}}{(2n+1)!} \;\; = \;\; x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} \pm \cdots \qquad \forall x \in \mathbb{R}. [/math]
Wir entwickeln andererseits den Sinus ausgehend von seinen Nullstellen als Produkt unendlich vieler Linearfaktoren.[A 1] Die Nullstellenmenge des Sinus ist [math]\{x \in \mathbb{R}: x = n\pi, \, n \in \mathbb{Z} \}[/math]. Daraus leitet sich instruktiv folgende Produktdarstellung für alle [math]x \in \mathbb{R}[/math] ab:[A 2]
- [math]\displaystyle \begin{align} \sin(x) \;\; &= \;\; x \cdot \prod_{n=1}^{\infty}\left(1 - \frac{x^2}{(n\pi)^2}\right) \\ &= \;\; x \left(1 - \frac{x^2}{\pi^2}\right) \left(1 - \frac{x^2}{(2\pi)^2}\right) \left(1 - \frac{x^2}{(3\pi)^2}\right) \left(1 - \frac{x^2}{(4\pi)^2}\right) \cdots \end{align} [/math]
Euler benutzte hier sozusagen heuristisch die Entwicklung des Sinus als „Polynom von unendlichem Grad“.[A 3] Nun multiplizieren wir das Produkt aus:[A 4]
- [math]\displaystyle \sin(x) \;\; = \;\; x + \left(-\frac{1}{\pi^2} -\frac{1}{(2\pi)^2} -\frac{1}{(3\pi)^2} -\frac{1}{(4\pi)^2} - \cdots \right)x^3 + \cdots \qquad \forall x \in \mathbb{R}. [/math]
Wegen der linearen Unabhängigkeit der Monome [math]x^k \, (k \in \mathbb{N})[/math] können wir einen Koeffizientenvergleich mit der Taylorreihe durchführen. Für den kubischen Term [math]x^3[/math] erhalten wir damit schließlich:
- [math]\displaystyle \begin{alignat}{2} &\qquad& - \frac{1}{3!} \;\; &= \;\; -\frac{1}{\pi^2} -\frac{1}{(2\pi)^2} -\frac{1}{(3\pi)^2} -\frac{1}{(4\pi)^2} - \cdots \\ &\Leftrightarrow& \frac{\pi^2}{6} \;\; &= \;\; \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \cdots \end{alignat} [/math]
∎
Formaler Beweis (1)
Die Idee des Beweises besteht darin, die Reihe [math]\sum_{n=1}^{\infty}\frac{1}{n^2}[/math] in ein (Doppel-)Integral zu überführen.[4] Dieses lässt sich dann mit einigen (elementaren!) Tricks und geschickten Substitutionen berechnen. Dafür benötigen wir lediglich den Satz von Fubini aus der Maß- und Integrationstheorie als nicht-elementares Resultat, das wir hier ohne Beweis verwenden möchten. Die Stellen, an denen dieses eingeht, sind im Folgenden mit [math](\ast)[/math] markiert. Wir spalten zunächst die Ausgangsreihe auf[A 5] und formen um:
- [math]\displaystyle \begin{alignat}{2} && \sum_{n=1}^{\infty}\frac{1}{n^2} \;\; &= \;\; \sum_{ \begin{array}{c} n\in\mathbb{N}, \\[-3pt] n \, \text{gerade} \end{array} }\frac{1}{n^2} \;\; + \sum_{ \begin{array}{c} n\in\mathbb{N}, \\[-3pt] n \, \text{ungerade} \end{array} }\frac{1}{n^2} \;\; = \;\; \sum_{n=1}^{\infty}\frac{1}{(2n)^2} \;\; + \sum_{n=1}^{\infty}\frac{1}{(2n-1)^2} \\ && &= \;\; \frac{1}{4} \cdot \sum_{n=1}^{\infty}\frac{1}{n^2} \;\; + \sum_{n=1}^{\infty}\frac{1}{(2n-1)^2} \\ &\Leftrightarrow& \qquad \sum_{n=1}^{\infty}\frac{1}{n^2} \;\; &= \;\; \frac{4}{3} \cdot \sum_{n=1}^{\infty}\frac{1}{(2n-1)^2} \end{alignat} [/math]
Um nun zu einer Integraldarstellung zu gelangen, beachten wir für [math]m \in \mathbb{N}_0[/math] die Beziehung
- [math]\displaystyle \begin{align} \int_{1}^{0} x^m \cdot \ln(x) \, dx \;\; &\overset{\text{part.}}{\underset{\text{Int.}}{=}} \;\; \underbrace{\left[\frac{1}{m+1} \cdot x^{m+1} \cdot \ln(x)\right]_1^0}_{=\; 0} \;\; - \int_{1}^{0} \frac{1}{m+1} \cdot x^{m+1} \cdot \frac{1}{x} \, dx \\ &= \;\; \frac{1}{m+1} \cdot \int_{0}^{1}x^m \, dx \;\; = \;\; \frac{1}{(m+1)^2}. \end{align} [/math]
Damit erhalten wir
- [math]\displaystyle \begin{align} \sum_{n=1}^{\infty}\frac{1}{n^2} \;\; &= \;\; \frac{4}{3} \cdot \sum_{n=1}^{\infty}\frac{1}{(2n-1)^2} \;\; \overset{\text{Index-}}{\underset{\text{shift}}{=}} \;\; \frac{4}{3} \cdot \sum_{n=0}^{\infty}\frac{1}{(2n+1)^2} \\ &= \;\; \frac{4}{3} \cdot \sum_{n=0}^{\infty} \int_{1}^{0} x^{2n} \cdot \ln(x) \, dx \;\; \overset{(\ast)}{=} \;\; \frac{4}{3} \cdot \int_{1}^{0} \left(\ln(x) \cdot \sum_{n=0}^{\infty}x^{2n}\right) \, dx \\ &\overset{\text{geom.}}{\underset{\text{Reihe}}{=}} \;\; \frac{4}{3} \cdot \int_{1}^{0} \frac{\ln(x)}{1-x^2} \, dx \;\; = \;\; \frac{4}{6} \cdot \int_{1}^{0} \frac{\ln(x^2)-\ln(1)}{1-x^2} \, dx. \end{align} [/math]
Im Integranden beobachten wir
- [math]\displaystyle \begin{align} \ln(x^2)-\ln(1) \;\; &= \;\; \left[\ln\left(\frac{1+x^2y^2}{1+y^2}\right)\right]_{y=0}^{y\to\infty} \;\; = \;\; \left[\ln(1+x^2y^2) - \ln(1+y^2)\right]_{y=0}^{y\to\infty} \\ &= \;\; \int_{0}^{\infty} \left(\frac{2x^2y}{1+x^2y^2} - \frac{2y}{1+y^2}\right) \, dy \end{align} [/math]
und folgern daraus:
- [math]\displaystyle \begin{align} \sum_{n=1}^{\infty}\frac{1}{n^2} \;\; &= \;\; \frac{4}{3} \cdot \int_{1}^{0} \frac{1}{1-x^2} \int_{0}^{\infty} \left(\frac{x^2y}{1+x^2y^2} - \frac{y}{1+y^2}\right) \, dy \, dx \\ &= \;\; \frac{4}{3} \cdot \int_{1}^{0} \frac{1}{1-x^2} \int_{0}^{\infty} \frac{y(x^2-1)}{(1+x^2y^2)(1+y^2)} \, dy \, dx \\ &\;\stackrel{(\ast)}{=} \,\;\; \frac{4}{3} \cdot \int_{0}^{\infty} \frac{y}{1+y^2} \int_{0}^{1} \frac{1}{1+x^2y^2} \, dx \, dy \end{align} [/math]
Das innere Standardintegral ist
- [math]\displaystyle \int_{0}^{1} \frac{1}{1+(xy)^2} \, dx \;\; = \;\; \left[\frac{\arctan(xy)}{y}\right]_{x=0}^{x=1} \;\; = \;\; \frac{\arctan(y)}{y} [/math]
und wir haben somit
- [math]\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^2} \;\; = \;\; \frac{4}{3} \cdot \int_{0}^{\infty} \frac{\arctan(y)}{1+y^2} \, dy. [/math]
Substituieren wir nun noch [math]u := \arctan(y)[/math] und nutzen die Ableitung [math]\frac{\mathrm{d}}{\mathrm{d}y}\arctan(y) = \frac{1}{1+y^2}[/math], so folgt schließlich:
- [math]\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^2} \;\; = \;\; \frac{4}{3} \cdot \int_{0}^{\frac{\pi}{2}} u \, du \;\; = \;\; \frac{\pi^2}{6} [/math]
∎
Formaler Beweis (2)
Als Zusatz geben wir noch einen weiteren interessanten Beweis an, der auf Fourier-Analysis beruht. Hierbei benötigen wir als Schlüssel die Parseval'sche Identität[5], die wir wieder ohne Beweis verwenden möchten. Diese erlaubt es, ähnlich wie in Beweis [math](1)[/math], die Reihe [math]\sum_{n=1}^{\infty}\frac{1}{n^2}[/math] auf die Berechnung eines (sehr leichten!) Integrals zurückzuführen. Ansonsten benötigen wir noch ein paar elementare Resultate der Fourier-Analysis sowie solche der komplexen Analysis.
Die Parseval'sche Gleichung für eine [math]2\pi[/math]-periodische, reellwertige Regelfunktion [math]f[/math] lautet
- [math]\displaystyle 2\pi \cdot \sum_{n \in \mathbb{Z}} |c_n|^2 \;\; = \;\; \int_{-\pi}^{\pi} |f(x)|^2 \, dx, [/math]
wobei die Fourierkoeffizienten [math]c_n[/math] von [math]f[/math] gegeben sind durch
- [math]\displaystyle c_n \;\; = \;\; \frac{1}{2\pi} \cdot \int_{-\pi}^{\pi} f(x) \cdot \mathrm{e}^{-\mathrm{i}nx} \, dx \qquad \forall n \in \mathbb{Z}. [/math]
Wir setzen [math]f(x) := x \; (x \in \mathbb{R})[/math] und berechnen mithilfe der Eulerformel [math]\mathrm{e}^{\mathrm{i}z} = \cos(z) + \mathrm{i} \cdot \sin(z) \; (z \in \mathbb{C})[/math] zunächst die Fourierkoeffizienten:
- [math]\displaystyle \begin{align} c_n \;\; &= \;\; \frac{1}{2\pi} \cdot \int_{-\pi}^{\pi} x \cdot \mathrm{e}^{-\mathrm{i}nx} \, dx \;\; \overset{\text{part.}}{\underset{\text{Int.}}{=}} \;\; \frac{1}{2\pi} \left( \left[\frac{\mathrm{i}}{n} \cdot x \cdot \mathrm{e}^{-\mathrm{i}nx}\right]_{-\pi}^{\pi} \;\; - \int_{-\pi}^{\pi} \frac{\mathrm{i}}{n} \cdot \mathrm{e}^{-\mathrm{i}nx} \, dx \right) \\ &= \;\; \frac{\mathrm{1}}{2\pi} \left( \frac{\mathrm{i}}{n} \left( \pi \mathrm{e}^{-\mathrm{i}n\pi} + \pi \mathrm{e}^{\mathrm{i}n\pi} \right) + \frac{1}{n^2} \left( \mathrm{e}^{-\mathrm{i}n\pi} - \mathrm{e}^{\mathrm{i}n\pi} \right) \right) \;\; \overset{\text{Euler-}}{\underset{\text{formel}}{=}} \;\; \frac{\mathrm{1}}{2\pi} \left( \frac{2\pi\mathrm{i}}{n}\cos(n\pi) - \frac{2\mathrm{i}}{n^2}\sin(n\pi) \right) \;\; \\ &= \;\; \frac{n\pi\cos(n\pi) - \sin(n\pi)}{\pi n^2}\mathrm{i} \;\; = \;\; \frac{\cos(n\pi)}{n}\mathrm{i} \;\; = \;\; \frac{(-1)^n}{n}\mathrm{i} \qquad \forall n \in \mathbb{Z} \setminus \{0\} \end{align} [/math]
und [math]c_0 = \frac{1}{2\pi} \int_{-\pi}^{\pi} x \, dx = 0[/math]. Damit ist also
- [math]\displaystyle |c_n|^2 \;\; = \;\; \begin{cases} \frac{1}{n^2}, \;\; \text{falls} \;\; n \neq 0 \\ 0, \;\; \text{falls} \;\; n=0 \end{cases}, [/math]
und Einsetzen in die Parseval'sche Gleichung liefert:
- [math]\displaystyle \begin{alignat}{2} && 2\pi \cdot \sum_{n \in \mathbb{Z} \setminus \{0\}} \frac{1}{n^2} \;\; &= \;\; \int_{-\pi}^{\pi} x^2 \, dx \;\; = \;\; \frac{2\pi^3}{3} \\ &\Leftrightarrow& \qquad \sum_{n=1}^{\infty} \frac{1}{n^2} \;\; &= \;\; \frac{\pi^2}{6} \end{alignat} [/math]
∎
Geometrischer Ansatz
Mittels einer Veranschaulichung soll gezeigt werden, wieso bei der Lösung des Basler Problems die Kreiszahl [math]\pi[/math] auftaucht und wo der geometrische Zusammenhang zu Kreisen liegt. Die Darstellung dieses Beispiels stammt aus einem Video des YouTube-Kanals 3Blue1Brown.[6] Hierzu wird ein theoretisches Beispiel aus der Physik verwendet, bestehend aus einem Beobachter und einer Menge von punktförmigen Lichtquellen, die alle mit derselben Intensität leuchten.
Bei einer Anordnung der Punktquellen auf einem Zahlenstrahl in positiver Richtung mit dem Beobachter im Ursprung entspricht die Frage nach der gesamten Intensität, die beim Beobachter ankommt, dem Basler Problem, denn aus der Physik ist für die Intensität [math]I[/math] und den Abstand [math]r[/math] folgende Relation bekannt: [math] I \sim \frac{1}{r^2}. [/math] Entspricht die Intensität einer Quelle, gemessen in einer Entfernung von [math]1[/math], einem Wert von [math]I = 1[/math], so ergibt sich für die gesamte Intensität ein Wert von [math] \sum_{n=1}^{\infty}\frac{1}{n^2}. [/math]
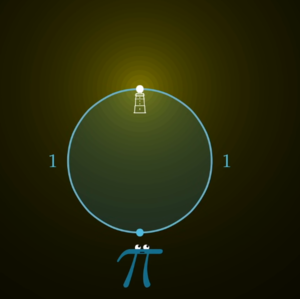
Stehe der Beobachter nun an einem Kreis mit Umfang 2. Wenn sich direkt gegenüber eine Punktquelle befindet, so ist die Entfernung zwischen Beobachter und Quelle [math]d = \frac{2}{\pi}[/math]. Also beträgt die Intensität, die beim Beobachter ankommt, [math]\frac{1}{d^2} = \frac{\pi^2}{4}[/math].
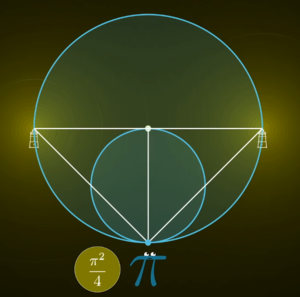
Nun betrachte man einen Kreis mit doppeltem Durchmesser um den „obersten Punkt“ des bisherigen Kreises. Legt man eine Gerade durch die Lichtquelle, die orthogonal zur Verbindungsgerade von Beobachter und Quelle ist, so schneidet diese den neuen Kreis in genau zwei Punkten. Wenn an diesen Punkten je eine Lichtquelle platziert wird, so ist deren gemeinsame Intensität beim Beobachter gleich der Intensität der ursprünglichen Quelle. (Dies lässt sich über die Entfernungen der Quellen mithilfe des Satzes von Pythagoras zeigen.) Insbesondere ist der Abstand zwischen den beiden neuen Quellen entlang des Kreises jeweils 2.
Nun wird dieser Schritt induktiv fortgesetzt (neuer Kreis mit doppeltem Durchmesser; je zwei neue Quellen auf dem neuen Kreis, die aus den bisherigen konstruiert werden). Hierdurch verdoppelt sich in jedem Schritt die Anzahl der Lichtquellen und der Abstand von einer Quelle zur nächsten entlang des Kreisumfangs ist immer 2. Die Gesamtintensität bleibt hiervon unbeeinflusst.
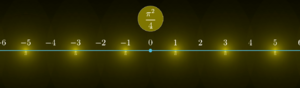
Im Grenzwert nähert sich dieses Verfahren einem Zahlenstrahl über die ganzen Zahlen an, mit Punktquellen auf den ungeraden Zahlen und dem Beobachter im Ursprung.
Da das Basler Problem nur positive Zahlen betrachtet, ist nur die rechte Seite des Strahls notwendig. Diese hat eine Gesamtintensität von [math]\frac{1}{2} \cdot \frac{\pi^2}{4} = \frac{\pi^2}{8}[/math]. Dies entspricht der Summe [math]\sum_{n=1}^{\infty}\frac{1}{(2n-1)^2}[/math].
Formt man das Basler Problem noch ein wenig um, so erhält man die gewünschte Lösung:
- [math]\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^2} \;\; \overset{\text{vgl.}}{\underset{\text{Beweis (1)}}{=}} \;\; \frac{4}{3} \cdot \sum_{n=1}^{\infty}\frac{1}{(2n-1)^2} \;\; = \;\; \frac{4}{3} \cdot \frac{\pi^2}{8} \;\; = \;\; \frac{\pi^2}{6}. [/math]
Ausblick
Die Lösung des Basler Problems ist eine explizite Berechnung eines Wertes der Riemann'schen [math]\zeta[/math]–Funktion.[7] Diese bekannte komplexwertige Funktion ist für [math]s \in \mathbb{C}[/math] mit [math]\operatorname{Re}(s) \gt 1[/math] definiert als
- [math]\displaystyle \zeta(s) \;\; = \;\; \sum_{n=1}^{\infty}\frac{1}{n^s}. [/math]
Analog zu Eulers Beweis des Basler Problems lässt sich für alle geraden natürlichen Zahlen [math]2k[/math] [math](k \in \mathbb{N})[/math] eine geschlossene (jedoch mitnichten einfache) Formel für die Werte von [math]\zeta(2k)[/math] angeben.
Die Riemann'sche [math]\zeta[/math]–Funktion spielt in der aktuellen mathematischen Forschung noch immer eine große Rolle. So basiert auf der [math]\zeta[/math]–Funktion die Riemann'sche Vermutung, ein bisher ungelöstes Problem der (nicht nur) Zahlentheorie, die auch zu den sieben Millenium–Problemen zählt.
Auch in der Informatik finden sich Anwendungen der Riemann'schen [math]\zeta[/math]–Funktion: Der auf der [math]\zeta[/math]–Funktion basierende Miller–Rabin–Test, ein „schneller“ Primzahltest, wird verwendet, um sehr große Primzahlen zu finden. Diese werden in der Kryptographie zur Verschlüsselung von Daten verwendet.
Anmerkungen
- ↑ Dafür benötigt man formal einige Eigenschaften für die Konvergenz unendlicher Produkte und ganz zentral den Produktsatz von Weierstraß aus der Funktionentheorie. Die angegebene Entwicklung ergibt sich dann als Lösung einer bestimmten Nullstellenverteilung. Das führt an dieser Stelle jedoch zu weit und wir wollen es bei einer intuitiv einleuchtenden Begründung belassen.
- ↑ Das gilt, genau wie die Taylorentwicklung des Sinus, sogar für alle komplexen Zahlen.
- ↑ Im Allgemeinen funktioniert dieser Ansatz nicht!
- ↑ Dafür benötigt man formal die Newtonidentitäten der Algebra.
- ↑ Beachte, dass beide Teilreihen unbedingt konvergieren.
Einzelnachweise
- ↑ Basel problem. (2021, 17. März). In Wikipedia. https://en.wikipedia.org/w/index.php?title=Basel_problem&oldid=1012692562
- ↑ W. Sullivan, B. (2013, 11. April). The Basel Problem, Numerous Proofs [Vorlesungsfolien]. Carnegie Mellon University, Department of Mathematical Sciences. https://www.math.cmu.edu/~bwsulliv/basel-problem.pdf
- ↑ Johann Beurich, „DorFuchs“. (2018, 1. März). Was die Summe der Kehrwerte der Quadratzahlen mit [math]\pi[/math] zu tun hat [Video]. YouTube. https://www.youtube.com/watch?v=CTYuVXNaFlk
- ↑ Michael Penn. (2020, 17. August). An interesting approach to the Basel problem! [Video]. YouTube. https://www.youtube.com/watch?v=-Yy_Jsw0djM
- ↑ Parseval’s identity. (2020, 22. September). In Wikipedia. https://en.wikipedia.org/w/index.php?title=Parseval%27s_identity&oldid=979799433
- ↑ Grant Sanderson, „3Blue1Brown“. (2018, 2. März). Why is pi here? And why is it squared? A geometric answer to the Basel problem [Video]. YouTube. https://www.youtube.com/watch?v=d-o3eB9sfls
- ↑ Riemannsche Zeta-Funktion. (2021, 18. Februar). In Wikipedia. https://de.wikipedia.org/w/index.php?title=Riemannsche_Zeta-Funktion&oldid=208969500
Autoren
Timo Dörzbach, Lucca Kümmerle, Robert Paus