Zufallsmatrizen - Bohemians und die geheimnisvolle Ordnung im Chaos: Unterschied zwischen den Versionen

Aus FunFacts Wiki
Zur Navigation springen Zur Suche springen
 
(45 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt)
Zeile 3: Zeile 3:
 
</gallery>
 
</gallery>
  
−
"Zufallsmatrix" - eine Matrix mit zufälligen Einträgen - klingt zuerst einmal vielleicht nach etwas Willkürlichem. Wie daraus solche faszinierenden [[Zufallsmatrizen_-_Bohemians_und_die_geheimnisvolle_Ordnung_im_Chaos#Galerie|Bilder]] entstehen, was man sonst noch alles damit anstellen kann und welche Möglichkeiten sich für die Forschung in der Physik und anderen Wissenschaften ergeben, soll in diesem Artikel gezeigt werden.
+
"Zufallsmatrix" - eine Matrix mit zufälligen Einträgen - klingt zuerst einmal vielleicht nach etwas Willkürlichem. Den Anstoß zur Forschung im Bereich der Zufallsmatrizen gab der Physiker Eugene Wigner. Seit seiner Entdeckung werden zufällige Matrizen in verschiedenen Bereichen der Quantenphysik verwendet, um dynamische Systeme zu beschreiben.
−
 
+
Wie daraus solche faszinierenden [[Zufallsmatrizen_-_Bohemians_und_die_geheimnisvolle_Ordnung_im_Chaos#Galerie|Bilder]] entstehen, was man sonst noch alles damit anstellen kann und welche Möglichkeiten sich für die Forschung in der Physik und anderen Wissenschaften ergeben, soll in diesem Artikel gezeigt werden.
−
Den Anstoß zur Forschung im Bereich der Zufallsmatrizen gab der Physiker Eugene Wigner, der bei der Analyse von schweren Atomkernen darauf stieß, dass das Resonanzspektrum schwerer Kerne bei hohen Energien durch die Eigenwerte von Zufallsmatrizen beschrieben werden kann.<ref name="wigner">Wigner, E."Characteristic vectors of bordered matrices with infinite dimensions", Annals of Mathematics (1955) 62, 548–564, doi:10.2307/1970079, jstor:1970079</ref> Seit dieser Entdeckung Wigners werden zufällige Matrizen in verschiedenen Bereichen der Quantenphysik verwendet, z.B. als spektrale Signatur von Quantenchaos, zur Beschreibung mesoskopischer Systeme mit Unordnung oder in der Quantenchromodynamik.<ref>Verbaarschot, J.J. und Wettig, T. "Random Matrix Theory and Chiral Symmetry in QCD", Annu. Rev. Nucl. Part. Sci. (2000) 50, 343–410, doi:10.1146/annurev.nucl.50.1.343, arxiv:hep-ph/0003017</ref> Das Vorkommen der Zufallsmatrizen in verschiedenen Bereichen zeigt, dass diese eine gewisse Universalität besitzen. Der stochastische Mechanismus, der zu solchen Verteilungen führt, ist bislang jedoch nicht allgemein verstanden. In den Spezialfällen, für die Beweise existieren, liegen explizite Formeln für die Verteilungen vor, die mit allerlei Tricks analysiert werden können. Die Beweise brechen allerdings schon bei kleinen Abwandlungen der Modelle in sich zusammen.
 
  
 
== Zufallsmatrizen ==
 
== Zufallsmatrizen ==
Zeile 17: Zeile 16:
 
Es gibt sehr viele Methoden, solche Matrizen auszuwählen, dabei kann die Wahrscheinlichkeitsverteilung der Einträge, oder die Form der Symmetrie der Matrizen sehr stark variieren. Wir betrachten nun  Matrizen, die symmetrisch bzgl. der Diagonale sind und deren Einträge unabhängig voneinander gemäß der Normalverteilung ausgewählt werden.
 
Es gibt sehr viele Methoden, solche Matrizen auszuwählen, dabei kann die Wahrscheinlichkeitsverteilung der Einträge, oder die Form der Symmetrie der Matrizen sehr stark variieren. Wir betrachten nun  Matrizen, die symmetrisch bzgl. der Diagonale sind und deren Einträge unabhängig voneinander gemäß der Normalverteilung ausgewählt werden.
  
−
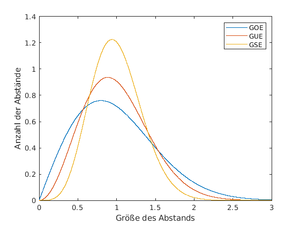
Lässt man die Größe dieser Matrizen gegen Unendlich gehen, ergeben die Abstände zwischen aufeinanderfolgenden Eigenwerten dieser Matrizen eine bestimmte Kurve (siehe Bild). Die Klasse der Zufallsmatrizen, deren Eigenwertabstände dieser Kurve folgen, nennt man ''gaußsches orthogonales Ensemble'' ''(GOE)''.<ref name="mehta">Mehta, M.L., "Random Matrices" (2004), Elsevier/Academic Press, Amsterdam. isbn:0-12-088409-7</ref>
+
Lässt man die Größe dieser Matrizen gegen Unendlich gehen, ergeben die Abstände zwischen aufeinanderfolgenden Eigenwerten dieser Matrizen eine bestimmte Kurve <ref name="mehta">Mehta, M.L., "Random Matrices" (2004), Elsevier/Academic Press, Amsterdam. isbn:0-12-088409-7</ref> (siehe Bild). Diese Kurven gehören zu den sogenannten Wigner-Verteilungen, benannt nach dem oben genannten Physiker [https://de.wikipedia.org/wiki/Eugene_Paul_Wigner Eugene Wigner]. Die Klasse der Zufallsmatrizen, deren Eigenwertabstände dieser Kurve folgen, nennt man ''gaußsches orthogonales Ensemble'' ''(GOE)''.<ref name="mehta">Mehta, M.L., "Random Matrices" (2004), Elsevier/Academic Press, Amsterdam. isbn:0-12-088409-7</ref>
  
 
Analog ergeben Eigenwertabstände von [https://de.wikipedia.org/wiki/Hermitesche_Matrix hermiteschen Zufallsmatrizen] eine andere Kurve, deren Klasse nennt man ''gaußsches unitäres Ensemble (GUE)''.
 
Analog ergeben Eigenwertabstände von [https://de.wikipedia.org/wiki/Hermitesche_Matrix hermiteschen Zufallsmatrizen] eine andere Kurve, deren Klasse nennt man ''gaußsches unitäres Ensemble (GUE)''.
  
−
{| class="mw-collapsible mw-collapsed"
+
Eine hermitesche Matrix ist eine Matrix mit komplexen Einträgen, die <math>\,{A}^T\ = \bar {A}\,</math>  erfüllt. D.h bei der Spiegelung wird das Vorzeichen des Imaginärteils gedreht (d.h. komplex konjugiert):  
−
|+ Beispiel hermitischer Matrix:
+
<math>\,\begin{pmatrix} 1 & 2 & 3+i  \\ 2 & 5 & 6-2i  \\ 3-i & 6+2i & 7  \end{pmatrix}\,</math>
−
|+
+
Ihre Eigenwerte sind alle reell.
−
| Eine hermitesche Matrix ist eine Matrix mit komplexen Einträgen, die <math>\,{A}^T\ = \bar {A}\,</math>  erfüllt. D.h bei der Spiegelung wird das Vorzeichen des Imaginärteils gedreht (d.h. komplex konjugiert):  
 
−
| <math>\,\begin{pmatrix} 1 & 2 & 3+i  \\ 2 & 5 & 6-2i  \\ 3-i & 6+2i & 7  \end{pmatrix}\,</math>
 
−
|
 
−
| Ihre Eigenwerte sind alle reell.
 
−
|}
 
  
−
Diese Kurven gehören zu den sogenannten Wigner-Verteilungen, benannt nach dem oben genannten Physiker [https://de.wikipedia.org/wiki/Eugene_Paul_Wigner Eugene Wigner].  
+
Die dritte Kurve die im Bild zu sehen ist, das ''gaußsche symplektische Ensemble (GSE)'', beschreibt das Verhalten von den sogenannten [https://de.wikipedia.org/wiki/Quaternion quaternionischen Zufallsmatrizen].
  
−
Seitdem wurden viele weitere Familien von Zufallsmatrizen untersucht und dabei andere Ensembles entdeckt, deren Eigenwertabstände anderen Kurven folgen. Man fand dabei heraus, dass diese Eigenwertabstände nicht von der Wahrscheinlichkeitsverteilung der Einträge abhängig sind, sondern nur von den Symmetrien der entsprechenden Matrizen. Der Grund dafür ist die extreme Größe der Matrizen. Dadurch heben sich nämlich die komplizierten Effekte der Eigenwertberechnung im Mittel auf, und die Funktion strebt gegen einen Durchschnittswert. Allerdings lassen sich diese universellen Eigenschaften schwer beweisen und bis heute gibt es noch viele offene Probleme in diesem Teilgebiet.
 
  
 
===Nicht universelle Eigenschaften===
 
===Nicht universelle Eigenschaften===
−
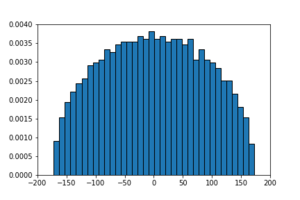
[[Datei:Halbkreis.png|mini|Eigenwertdichte von einer symmetrischen 1500x1500 Matrix mit Einträgen aus einer Normalverteilung|alternativtext=]]
+
[[Datei:Halbkreis.png|mini|Eigenwertdichte von einer symmetrischen <math>1500 \times 1500 </math> Matrix mit Einträgen aus einer Normalverteilung|alternativtext=]]
 
Eine Eigenschaft einer Zufallsmatrix ist nicht universell, wenn sie von der Wahrscheinlichkeitsverteilung der Einträge abhängt, ein Beispiel dafür ist die Dichte der Eigenwerte. Allerdings gibt es auch hier interessante Gesetzmäßigkeiten, wie zum Beispiel die sogenannten Wigner-Halbkreise.  
 
Eine Eigenschaft einer Zufallsmatrix ist nicht universell, wenn sie von der Wahrscheinlichkeitsverteilung der Einträge abhängt, ein Beispiel dafür ist die Dichte der Eigenwerte. Allerdings gibt es auch hier interessante Gesetzmäßigkeiten, wie zum Beispiel die sogenannten Wigner-Halbkreise.  
−
Dabei handelt es sich wieder um symmetrische Zufallsmatrizen, deren Einträge gemäß der Normalverteilung ausgewählt werden. Diesmal trägt man nicht die Eigenwertabstände in einem Histogramm auf, sondern die Häufigkeit von einzelnen Eigenwerten. Dies ergibt einen Halbkreis mit Mittelpunkt im Ursprung. Je größer die Zufallsmatrizen sind, desto mehr nähert sich das Histogramm einem Halbkreis an.
+
Dabei handelt es sich wieder um symmetrische Zufallsmatrizen, deren Einträge gemäß der Normalverteilung ausgewählt werden. Diesmal trägt man nicht die Eigenwertabstände in einem Histogramm auf, sondern die Häufigkeit von Eigenwerten. Je größer die Zufallsmatrizen sind, desto mehr nähert sich das Histogramm einem Halbkreis mit Mittelpunkt im Ursprung an.
  
 
=== Anwendungsgebiete ===
 
=== Anwendungsgebiete ===
−
Zufallsmatrizen können in den unterschiedlichsten, teils überraschenden Themengebieten genutzt werden, um (Natur-)Phänomene zu beschreiben oder Daten zu modellieren.  
+
Zufallsmatrizen werden in den unterschiedlichsten, teils überraschenden Themengebieten genutzt, um (Natur-)Phänomene zu beschreiben oder Daten zu modellieren.  
  
 
So etwa bei:
 
So etwa bei:
−
* Verknüpfung von Neuronen im Gehirn, künstlicher Intelligenz und maschinellem Lernen
+
* Verknüpfung von Neuronen im Gehirn, künstlicher Intelligenz und maschinellem Lernen <ref>Zhenyu Liao. A random matrix framework for large dimensional machine learning and neural networks. Other. Université Paris-Saclay, 2019. English. NNT: 2019SACLC068. HAL-Id: tel-02397287</ref>
−
* Datenkompression/Signalübertragung, Mobilfunk
+
* Datenkompression/Signalübertragung, Mobilfunk <ref>Antonia M. Tulino, Sergio Verdú: Random Matrix Theory and Wireless Communications. Now, 2004.</ref>
−
* Finanzwirtschaft (Fluktuation von Börsenkursen)
+
* Finanzwirtschaft (Fluktuation von Börsenkursen) <ref>http://web.mit.edu/sea06/agenda/talks/Harding.pdf</ref>
−
* der Statistik ankommender U-Bahnen in New York<ref>https://de.linkfang.org/wiki/Zufallsmatrix</ref>, Abstände parkender Autos und von Bäumen im Urwald
+
* der Statistik ankommender U-Bahnen in New York <ref name=":0">https://de.linkfang.org/wiki/Zufallsmatrix</ref>, Abstände parkender Autos und von Bäumen im Urwald
  
 
Warum genau es so gut funktioniert, diese doch sehr unterschiedlichen Dinge treffend durch Zufallsmatrizen zu beschreiben, ist überwiegend unbekannt.
 
Warum genau es so gut funktioniert, diese doch sehr unterschiedlichen Dinge treffend durch Zufallsmatrizen zu beschreiben, ist überwiegend unbekannt.
Zeile 67: Zeile 60:
  
 
==== Quantenmechanik ====
 
==== Quantenmechanik ====
−
Die Untersuchung schwerer Atomkerne bzw. das Messen ihrer unterschiedlichen Energieniveaus ist nicht ganz einfach und wird mithilfe der [https://de.wikipedia.org/wiki/Schrödingergleichung Schrödingergleichung] beschrieben.  
+
Die Quantenmechanik beschäftigt sich mit den physikalischen Eigenschaften und Gesetzmäßigkeiten der Natur auf atomarer und subatomarer Ebene. Zufallsmatrizen können im Rahmen der Quantenmechanik z. B. bei magnetischen Systemen<ref>VS Rychkov, S Borlenghi, H Jaffres, A Fert, X Waintal: Spin Torque and Waviness in Magnetic Multilayers: A Bridge Between Valet-Fert Theory and Quantum Approaches. In: Phys. Rev. Lett.. 103, Nr. 6, August 2009, S. 066602. doi:10.1103/PhysRevLett.103.066602 . PMID 19792592.</ref>, dem Quanten-Hall-Effekt <ref>DJE Callaway: Random Matrices, Fractional Statistics, and the Quantum Hall Effect. In: Phys. Rev., B Condens. Matter. 43, Nr. 10, April 1991, S. 8641–8643. doi:10.1103/PhysRevB.43.8641 . PMID 9996505.</ref>, Supraleitern<ref>SR Bahcall: Random Matrix Model for Superconductors in a Magnetic Field. In: Phys. Rev. Lett.. 77, Nr. 26, Dezember 1996, S. 5276–5279. doi:10.1103/PhysRevLett.77.5276 . PMID 10062760.</ref>, Quanten-Dots <ref>DM Zumbühl, JB Miller, CM Marcus, K Campman, AC Gossard: Spin-orbit Coupling, Antilocalization, and Parallel Magnetic Fields in Quantum Dots. In: Phys. Rev. Lett.. 89, Nr. 27, Dezember 2002, S. 276803. doi:10.1103/PhysRevLett.89.276803 . PMID 12513231.</ref>, Quantengravitation <ref>F Franchini, VE Kravtsov: Horizon in Random Matrix Theory, the Hawking Radiation, and Flow of Cold Atoms. In: Phys. Rev. Lett.. 103, Nr. 16, Oktober 2009, S. 166401. doi:10.1103/PhysRevLett.103.166401 . PMID 19905710.</ref> und schweren Atomkernen <ref name=":0" /> eingesetzt werden. 
−
 
 
−
<math>\mathrm i \hbar \frac{\partial \psi}{\partial t} = - \frac{\hbar^2}{2m} \nabla^2 \psi + V \psi</math> betrachtet (<math>\hbar</math> ist die [https://de.wikipedia.org/wiki/Plancksches_Wirkungsquantum#Reduziertes_Plancksches_Wirkungsquantum reduzierte Plancksche Konstante]). In diesem Zusammenhang erwähnenswert ist der sogenannte [https://de.wikipedia.org/wiki/Hamiltonoperator Hamilton-Operator], welcher angewendet auf den Zustand eines quantenmechanischen Systems dessen zeitliche Entwicklung beschreibt.
 
−
 
 
−
Wenn man nun <math>H \psi := \mathrm i \hbar \frac{\partial \psi}{\partial t}</math> sowie <math>E \psi := - \frac{\hbar^2}{2m} \nabla^2 \psi + V \psi</math> definiert, kann die erste Gleichung vereinfacht als <math>H \psi = E \psi</math> geschrieben werden. <math>H</math> ist der Hamilton-Operator, <math>\psi</math> ein Eigenvektor und <math>E</math> der korrespondierende Eigenwert, hinter welchem sich die verschiedenen Energieniveaus verbergen. Auch die allgemeinste  Form der Schrödingergleichung <math>\mathrm{i}\hbar\frac{\partial}{\partial t} |\,\psi (t) \rangle = \hat{H} |\,\psi (t) \rangle</math> (wobei <math>\hat{H}</math> der Hamilton-Operator und <math>|\,\psi (t) \rangle</math> der Zustandsvektor sind) macht den Zusammenhang zu Eigenwerten sichtbarer.
 
−
 
 
−
Nach Eugene Wigner kann nun, statt mit dem komplizierten Hamilton-Operator (welcher auf einem unendlich-dimensionalen Vektorraum definiert ist) zu arbeiten, die Verteilung der Eigenwerte einer Familie von Zufallsmatrizen betrachtet werden, um auf die Verteilung der Energieniveaus zu schließen. Dies geschieht, indem man nach Werten sucht, gegen welche diese Verteilung läuft (asymptotisches Verhalten), wenn die Größe dieser Matrizen gegen unendlich geht.<ref>https://math.uni.lu/eml/projects/reports/random-matrices.pdf</ref>
 
  
−
<math>\mathrm i \hbar \frac{\partial \psi}{\partial t} = - \frac{\hbar^2}{2m} \nabla^2 \psi + V \psi</math>Schrödingergleichung
+
Eugene Wigner stieß bei der Analyse von schweren Atomkernen darauf, dass das Resonanzspektrum schwerer Kerne bei hohen Energien durch die Eigenwerte von Zufallsmatrizen beschrieben werden kann. Um auf die Verteilung der Energieniveaus zu schließen, wird die Verteilung der Eigenwerte einer Familie von Zufallsmatrizen betrachtet. Dies geschieht, indem man nach Werten sucht, gegen welche diese Distribution läuft (asymptotisches Verhalten), wenn die Größe dieser Matrizen gegen unendlich geht.<ref name="wigner">Wigner, E."Characteristic vectors of bordered matrices with infinite dimensions", Annals of Mathematics (1955) 62, 548–564, doi:10.2307/1970079, jstor:1970079</ref> Das häufige Vorkommen der Verteilungsfunktionen lokaler Eigenwertstatistiken von Zufallsmatrizen in Mathematik und Quantenphysik legt nahe, dass diese eine gewisse Universalität besitzen. Der Mechanismus, der dem zugrunde liegt, ist bislang jedoch noch nicht allgemein verstanden.<ref name="guhr">T.  Guhr,  A.  Müller–Groeling  und  H.  A.  Weidenmüller.  Random-matrix  theories  in quantum physics: common concepts. Physics Reports,299, 189–425, 1998.</ref>
  
 
== Bohemian Matrices ==
 
== Bohemian Matrices ==
Zeile 81: Zeile 68:
  
 
Bohemian Matrices sind Zufallsmatrizen, deren Einträge auf eine Menge ganzer Zahlen aus einem endlichen Intervall beschränkt sind, wie z. B. <math>\{-1, 0, 1\}</math>. Die ausgewählten Zahlen sind dabei unabhängig von der Dimension der Matrix. Das Feld der Bohemian Matrices umfasst mittlerweile auch Matrizen mit Einträgen aus kontinuierlichen bzw. nicht-endlichen Mengen, obwohl diese nach dieser Namensgebung streng genommen nicht mit inbegriffen wären.<ref>https://ir.lib.uwo.ca/etd/6069/</ref> Zusätzlich kann eine bestimmte Struktur der Matrix vorgegeben werden (z. B. Diagonalmatrix, Dreiecksmatrix etc.).  
 
Bohemian Matrices sind Zufallsmatrizen, deren Einträge auf eine Menge ganzer Zahlen aus einem endlichen Intervall beschränkt sind, wie z. B. <math>\{-1, 0, 1\}</math>. Die ausgewählten Zahlen sind dabei unabhängig von der Dimension der Matrix. Das Feld der Bohemian Matrices umfasst mittlerweile auch Matrizen mit Einträgen aus kontinuierlichen bzw. nicht-endlichen Mengen, obwohl diese nach dieser Namensgebung streng genommen nicht mit inbegriffen wären.<ref>https://ir.lib.uwo.ca/etd/6069/</ref> Zusätzlich kann eine bestimmte Struktur der Matrix vorgegeben werden (z. B. Diagonalmatrix, Dreiecksmatrix etc.).  
−
 
−
 
 
=== Wie macht man daraus Bilder? ===
 
=== Wie macht man daraus Bilder? ===
 
Um die Eigenwerte der Zufallsmatrizen zu visualisieren, wird zunächst ein Satz von Matrizen nach dem gewünschten Muster generiert. Die Anzahl liegt dabei meist zwischen <math> 10^6</math> und <math>10^7</math> und die Größe etwa zwischen <math>3 \times 3 </math> und <math>20 \times 20 </math>. Bei nur schwach zu sehenden Mustern müssen teilweise auch deutlich mehr Matrizen einberechnet werden, um ein besseres Bild zu erhalten.
 
Um die Eigenwerte der Zufallsmatrizen zu visualisieren, wird zunächst ein Satz von Matrizen nach dem gewünschten Muster generiert. Die Anzahl liegt dabei meist zwischen <math> 10^6</math> und <math>10^7</math> und die Größe etwa zwischen <math>3 \times 3 </math> und <math>20 \times 20 </math>. Bei nur schwach zu sehenden Mustern müssen teilweise auch deutlich mehr Matrizen einberechnet werden, um ein besseres Bild zu erhalten.
Zeile 119: Zeile 104:
  
 
<gallery mode="packed" widths="300" heights="300">
 
<gallery mode="packed" widths="300" heights="300">
−
Datei:Image-6.png|mini|Eigenwertdichte von 20 Millionen <math>12 \times 12</math> oberer Hessenbergmatrizen mit [https://de.wikipedia.org/wiki/Toeplitz-Matrix Toeplitz-Struktur] und Einträgen aus der Menge <math>\{-1, 0, 1\}</math>
+
Datei:Image-6.png|mini|Eigenwertdichte von 20 Millionen <math>12 \times 12</math> oberen Hessenbergmatrizen mit [https://de.wikipedia.org/wiki/Toeplitz-Matrix Toeplitz-Struktur] und Einträgen aus der Menge <math>\{-1, 0, 1\}</math>
 
Datei:Image-11.png|mini|Eigenwertdichte von 10 Millionen <math>10 \times 10</math> Tridiagonalmatrizen mit Einträgen aus der Menge <math>\{-π, π\}</math>
 
Datei:Image-11.png|mini|Eigenwertdichte von 10 Millionen <math>10 \times 10</math> Tridiagonalmatrizen mit Einträgen aus der Menge <math>\{-π, π\}</math>
 
</gallery>
 
</gallery>
Zeile 126: Zeile 111:
 
Hier wurden Matrizen von der Form
 
Hier wurden Matrizen von der Form
 
<math>\,\begin{pmatrix} 0 & 0 & 0 & A \\ -1 & -1 & 0 & 0 \\ B & 0 & 0 & 0 \\ -1 & 1 & 1 & -1 \end{pmatrix}\,</math>
 
<math>\,\begin{pmatrix} 0 & 0 & 0 & A \\ -1 & -1 & 0 & 0 \\ B & 0 & 0 & 0 \\ -1 & 1 & 1 & -1 \end{pmatrix}\,</math>
−
verwendet. Die Einträge A und B wurden dabei zufällig aus einem kontinuierlichen Intervall ausgewählt.  
+
verwendet. Die Einträge A und B wurden dabei zufällig (gleichverteilt) aus einem kontinuierlichen Intervall ausgewählt.  
  
 
Kleine Änderungen an den Einträgen der Matrix können dabei vollkommen unterschiedliche Formen hervorbringen. Für die Bilder wurde die obige Matrix teilweise leicht verändert und es wurden unterschiedliche Intervallgrenzen ausgewählt.
 
Kleine Änderungen an den Einträgen der Matrix können dabei vollkommen unterschiedliche Formen hervorbringen. Für die Bilder wurde die obige Matrix teilweise leicht verändert und es wurden unterschiedliche Intervallgrenzen ausgewählt.
Zeile 136: Zeile 121:
  
 
== Einzelnachweise und Quellen ==
 
== Einzelnachweise und Quellen ==
−
<references />letzter Zugriff für alle: 30.03.2021
+
<references />letzter Zugriff für alle: 13.04.2021
 
*
 
*
  
 
== Autoren ==
 
== Autoren ==
 
Silas Janke, Lea Homann, Daniel Gáspár, Falk Loewner
 
Silas Janke, Lea Homann, Daniel Gáspár, Falk Loewner

Aktuelle Version vom 13. April 2021, 19:03 Uhr

  • Titel2.jpg

"Zufallsmatrix" - eine Matrix mit zufälligen Einträgen - klingt zuerst einmal vielleicht nach etwas Willkürlichem. Den Anstoß zur Forschung im Bereich der Zufallsmatrizen gab der Physiker Eugene Wigner. Seit seiner Entdeckung werden zufällige Matrizen in verschiedenen Bereichen der Quantenphysik verwendet, um dynamische Systeme zu beschreiben. Wie daraus solche faszinierenden Bilder entstehen, was man sonst noch alles damit anstellen kann und welche Möglichkeiten sich für die Forschung in der Physik und anderen Wissenschaften ergeben, soll in diesem Artikel gezeigt werden.

Zufallsmatrizen

Definition

Eine Zufallsmatrix ist eine Matrix, deren Einträge aus einen vorher festgelegten Stichprobe von (komplexen) Zahlen gemäß einer vorbestimmten Wahrscheinlichkeitsverteilung ausgewählt werden.[1]

Universelle Eigenschaften

Kurven der Wigner-Verteilungen

Universelle Eigenschaften einer Zufallsmatrix sind Eigenschaften, die nicht von der Wahrscheinlichkeitsverteilung der Einträge abhängen. Also es ist egal, ob man die Einträge der Matrizen gemäß einer Normalverteilung, einer Beta-Verteilung oder einer anderen Wahrscheinlichkeitsverteilung auswählt, die Eigenschaften, die dabei zu beobachten sind, bleiben gleich. Es gibt sehr viele Methoden, solche Matrizen auszuwählen, dabei kann die Wahrscheinlichkeitsverteilung der Einträge, oder die Form der Symmetrie der Matrizen sehr stark variieren. Wir betrachten nun Matrizen, die symmetrisch bzgl. der Diagonale sind und deren Einträge unabhängig voneinander gemäß der Normalverteilung ausgewählt werden.

Lässt man die Größe dieser Matrizen gegen Unendlich gehen, ergeben die Abstände zwischen aufeinanderfolgenden Eigenwerten dieser Matrizen eine bestimmte Kurve [2] (siehe Bild). Diese Kurven gehören zu den sogenannten Wigner-Verteilungen, benannt nach dem oben genannten Physiker Eugene Wigner. Die Klasse der Zufallsmatrizen, deren Eigenwertabstände dieser Kurve folgen, nennt man gaußsches orthogonales Ensemble (GOE).[2]

Analog ergeben Eigenwertabstände von hermiteschen Zufallsmatrizen eine andere Kurve, deren Klasse nennt man gaußsches unitäres Ensemble (GUE).

Eine hermitesche Matrix ist eine Matrix mit komplexen Einträgen, die [math]\,{A}^T\ = \bar {A}\,[/math] erfüllt. D.h bei der Spiegelung wird das Vorzeichen des Imaginärteils gedreht (d.h. komplex konjugiert): [math]\,\begin{pmatrix} 1 & 2 & 3+i \\ 2 & 5 & 6-2i \\ 3-i & 6+2i & 7 \end{pmatrix}\,[/math] Ihre Eigenwerte sind alle reell.

Die dritte Kurve die im Bild zu sehen ist, das gaußsche symplektische Ensemble (GSE), beschreibt das Verhalten von den sogenannten quaternionischen Zufallsmatrizen.


Nicht universelle Eigenschaften

Eigenwertdichte von einer symmetrischen [math]1500 \times 1500 [/math] Matrix mit Einträgen aus einer Normalverteilung

Eine Eigenschaft einer Zufallsmatrix ist nicht universell, wenn sie von der Wahrscheinlichkeitsverteilung der Einträge abhängt, ein Beispiel dafür ist die Dichte der Eigenwerte. Allerdings gibt es auch hier interessante Gesetzmäßigkeiten, wie zum Beispiel die sogenannten Wigner-Halbkreise. Dabei handelt es sich wieder um symmetrische Zufallsmatrizen, deren Einträge gemäß der Normalverteilung ausgewählt werden. Diesmal trägt man nicht die Eigenwertabstände in einem Histogramm auf, sondern die Häufigkeit von Eigenwerten. Je größer die Zufallsmatrizen sind, desto mehr nähert sich das Histogramm einem Halbkreis mit Mittelpunkt im Ursprung an.

Anwendungsgebiete

Zufallsmatrizen werden in den unterschiedlichsten, teils überraschenden Themengebieten genutzt, um (Natur-)Phänomene zu beschreiben oder Daten zu modellieren.

So etwa bei:

  • Verknüpfung von Neuronen im Gehirn, künstlicher Intelligenz und maschinellem Lernen [3]
  • Datenkompression/Signalübertragung, Mobilfunk [4]
  • Finanzwirtschaft (Fluktuation von Börsenkursen) [5]
  • der Statistik ankommender U-Bahnen in New York [6], Abstände parkender Autos und von Bäumen im Urwald

Warum genau es so gut funktioniert, diese doch sehr unterschiedlichen Dinge treffend durch Zufallsmatrizen zu beschreiben, ist überwiegend unbekannt.

Nicht nur in praktischen Anwendungsgebieten werden Zufallsmatrizen benutzt: Auch bei theoretischen Problemen in der Mathematik, wie dem Beweis der Riemannschen Vermutung, sind Zufallsmatrizen ein vielversprechender Ansatz[7], zu einer Lösung zu gelangen. Beispielsweise über eine (hypothetische) Matrix, von den Wissenschaftlern Riemannium getauft, deren Eigenwerte den Nullstellen der Riemannschen Zeta-Funktion entsprechen. Es gibt eine Verbindung zur Hilbert–Pólya Vermutung.

Eine Klasse von Zufallsmatrizen, die besonders viel mit der Dichte von Eigenwerten zu tun hat, ist die sogenannte Klasse der Bohemian Matrices. Auch Fraktale wie Julia- und Mandelbrotmengen tauchen im Zusammenhang mit Zufallsmatrizen auf (vgl. Bohemians mit Einträgen aus diskreter Menge, sowie die externe Galerie [1]).

Im Folgenden werden beispielhaft zwei sehr unterschiedliche Anwendungsgebiete genauer ausgeführt.

Bildverarbeitung

Zufallsmatrizen sind jedem von uns sicherlich schon einmal in einem ihrer praktischen Anwendungsgebiete begegnet: Der digitalen Bildverarbeitung.

Bei der Aufnahme von Fotos begegnet man oft dem sogenannten Bildrauschen, bei dem ein Bild störende Pixel aufweist, die in Farbe und Helligkeit deutlich vom eigentlichen Bild abweichen. Dies tritt vor allem bei einer schlechten Belichtungssituation, wie während der Dämmerung oder nachts, auf.

Es existieren verschiedene Arten von derartigen Bildstörungen, u. a. das Gaußsche Rauschen, dessen Wahrscheinlichkeitsdichte mithilfe der Normalverteilung als Formel beschrieben werden kann: [math]\frac{1}{\sqrt{2 \cdot \pi \cdot \sigma^2}} \cdot e^{-\frac{x^2}{2 \cdot \sigma^2}}[/math].

Unter der Annahme, dass jede zu diesen Pixeln assoziierte Matrix zufällig ist und damit ihre Eigenwertdichte berechenbar ist, kann man, indem man herausfindet, in welchem Maße sich der Eigenwert des Originalbilds zu dem des verrauschten Bildes verändert, das störende Gaußsche Rauschen eliminieren. Dabei werden die wichtigen Informationen des Originalbildes beibehalten.[8]

Quantenmechanik

Die Quantenmechanik beschäftigt sich mit den physikalischen Eigenschaften und Gesetzmäßigkeiten der Natur auf atomarer und subatomarer Ebene. Zufallsmatrizen können im Rahmen der Quantenmechanik z. B. bei magnetischen Systemen[9], dem Quanten-Hall-Effekt [10], Supraleitern[11], Quanten-Dots [12], Quantengravitation [13] und schweren Atomkernen [6] eingesetzt werden.

Eugene Wigner stieß bei der Analyse von schweren Atomkernen darauf, dass das Resonanzspektrum schwerer Kerne bei hohen Energien durch die Eigenwerte von Zufallsmatrizen beschrieben werden kann. Um auf die Verteilung der Energieniveaus zu schließen, wird die Verteilung der Eigenwerte einer Familie von Zufallsmatrizen betrachtet. Dies geschieht, indem man nach Werten sucht, gegen welche diese Distribution läuft (asymptotisches Verhalten), wenn die Größe dieser Matrizen gegen unendlich geht.[14] Das häufige Vorkommen der Verteilungsfunktionen lokaler Eigenwertstatistiken von Zufallsmatrizen in Mathematik und Quantenphysik legt nahe, dass diese eine gewisse Universalität besitzen. Der Mechanismus, der dem zugrunde liegt, ist bislang jedoch noch nicht allgemein verstanden.[15]

Bohemian Matrices

Bohemian Matrices sind eine bestimmte Form von Zufallsmatrizen. Der Name Bohemian steht dabei für bounded height integer matrix eigenvalues, woraus aus der Abkürzung BHIME dann Bohemian wurde. Ihre Untersuchung ist ein recht neues und noch relativ unerforschtes Gebiet und wird bislang im Rahmen der angewandten Mathematik betrachtet. Durchleuchtet werden dabei bspw. die Verteilung der Eigenwerte, ihre Symmetrien sowie Zahlenfolgen, die sich aus ihren Eigenschaften ergeben. Diese weisen überraschend oft Querverbindungen mit anderen Bereichen der Mathematik auf.[16]

Bohemian Matrices sind Zufallsmatrizen, deren Einträge auf eine Menge ganzer Zahlen aus einem endlichen Intervall beschränkt sind, wie z. B. [math]\{-1, 0, 1\}[/math]. Die ausgewählten Zahlen sind dabei unabhängig von der Dimension der Matrix. Das Feld der Bohemian Matrices umfasst mittlerweile auch Matrizen mit Einträgen aus kontinuierlichen bzw. nicht-endlichen Mengen, obwohl diese nach dieser Namensgebung streng genommen nicht mit inbegriffen wären.[17] Zusätzlich kann eine bestimmte Struktur der Matrix vorgegeben werden (z. B. Diagonalmatrix, Dreiecksmatrix etc.).

Wie macht man daraus Bilder?

Um die Eigenwerte der Zufallsmatrizen zu visualisieren, wird zunächst ein Satz von Matrizen nach dem gewünschten Muster generiert. Die Anzahl liegt dabei meist zwischen [math] 10^6[/math] und [math]10^7[/math] und die Größe etwa zwischen [math]3 \times 3 [/math] und [math]20 \times 20 [/math]. Bei nur schwach zu sehenden Mustern müssen teilweise auch deutlich mehr Matrizen einberechnet werden, um ein besseres Bild zu erhalten.

Von diesen Matrizen werden dann die Eigenwerte und deren Dichte berechnet, das heißt je häufiger ein Eigenwert in den Matrizen vorkommt, desto stärker fällt dieser ins Gewicht.

Real- und Imaginärteil der Eigenwertdichte werden dann in der komplexen Zahlenebene aufgetragen, wobei die Farbe nach einem vorher ausgewählten Farbschema festgelegt wird. Dazu wird eine Farbpalette ausgewählt, von der jede Farbe mit einer Dichte (zwischen 0 und 1) korrespondiert. Wenn der gleiche Eigenwert besonders häufig vorkommt, ändert dieser Pixel also entsprechend die Farbe im Bild.

Der Code zum Berechnen der Bilder ist frei verfügbar für Python: https://github.com/BohemianMatrices/bohemian-python und Matlab: https://github.com/BohemianMatrices/BHIME-Project. Die Bilder in diesem Artikel wurden in Matlab generiert.

Galerie

Je nachdem, wie man die Einträge und die Struktur einer Zufallsmatrix auswählt, kommen bei der Betrachtung der Eigenwertdichte unterschiedliche Muster und Formen zustande. In dieser Galerie sollen einige davon mit den zugehörigen Bildern vorgestellt werden. Es handelt sich bei allen Bildern um unsere Eigenkreationen (no pun intended).

Zufällige Matrix mit Einträgen aus diskreter Menge

Die wohl einfachste Art von Zufallsmatrizen sind [math]n\times n[/math] Matrizen, bei denen jeder Eintrag zufällig aus einer endlichen Menge von vorher festgelegten Werten ausgewählt wird. Dabei entstehen Muster mit teilweise selbstähnlich aussehenden Strukturen entlang der reellen Achse.

  • Eigenwertdichte von 10 Millionen [math]6 \times 6 \:[/math] Matrizen mit Einträgen aus der Menge [math] \{-1, -\frac{1}{1000}, 0, \frac{1}{1000}, 1\} [/math]

  • Zoom in die Mitte des linken Bildes

  • "Eigenkäfer" - Eigenwertdichte von 10 Millionen [math]6 \times 6\:[/math]Matrizen mit Einträgen aus der Menge [math] \{-1, -\frac{1}{100}, 0, \frac{1}{1000}, 12\} [/math]

Betaverteilung

Bei diesen Matrizen werden alle Einträge zufällig aus einer Betaverteilung mit vorher festgelegten Parametern [math] \alpha [/math] und [math] \beta [/math] generiert, die die Form der Verteilung charakterisieren. Zusätzlich wird eine Amplitude und Verschiebung hinzugefügt, sodass die Einträge von der Form [math]A \cdot x+b[/math] sind, wobei [math]x[/math] der Wert aus der Betaverteilung ist. Dadurch entstehen je nach Wahl der Parameter Linienmuster, auf denen sich die Eigenwerte häufen.

  • Eigenwertdichte von 15 Millionen [math]6\times 6[/math] Matrizen mit Werten aus einer Betaverteilung mit den Parametern [math] \alpha = 0{,}001, \: \beta = 0{,}001 [/math] (die Eigenwerte wurden an der imaginären Achse gespiegelt)

  • Eigenwertdichte von 5 Millionen [math]3\times 3[/math] Matrizen mit Werten aus einer Betaverteilung mit den Parametern [math] \alpha = 0{,}01, \: \beta = 0{,}01, \: A=5, \: b=-0{,}5[/math] (die Eigenwerte wurden an der imaginären Achse gespiegelt)

  • Eigenwertdichte von 30 Millionen [math]6\times 6[/math] Matrizen mit Werten aus einer Betaverteilung mit den Parametern [math] \alpha = 0{,}001, \: \beta = 0{,}01, \: A=5, \: b=-2 [/math] (die Eigenwerte wurden an der imaginären Achse gespiegelt)

Obere Hessenbergmatrix / Tridiagonalmatrix

Eine obere Hessenbergmatrix ist ähnlich wie eine obere Dreiecksmatrix, nur dass diese auch Einträge auf der ersten Nebendiagonalen unter der Hauptdiagonalen besitzt.

Beispielsweise ist [math]\,\begin{pmatrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 0 & 9 & 10 & 11 \\ 0 & 0 & 12 & 13 \end{pmatrix}\,[/math] eine obere Hessenbergmatrix. Analog ist [math]\,\begin{pmatrix} 1 & 2 & 0 & 0 \\ 3 & 4 & 5 & 0 \\ 6 & 7 & 8 & 9 \\ 10 & 11 & 12 & 13 \end{pmatrix}\,[/math] eine untere Hessenbergmatrix.

Eine Tridiagonalmatrix ist sowohl eine obere als auch eine untere Hessenbergmatrix und hat somit nur Einträge auf der Hauptdiagonalen und den beiden angrenzenden Nebendiagonalen, wie z. B. [math]\,\begin{pmatrix} 1 & 2 & 0 & 0 \\ 3 & 4 & 5 & 0 \\ 0 & 6 & 7 & 8 \\ 0 & 0 & 9 & 10 \end{pmatrix}\,[/math].

  • Eigenwertdichte von 20 Millionen [math]12 \times 12[/math] oberen Hessenbergmatrizen mit Toeplitz-Struktur und Einträgen aus der Menge [math]\{-1, 0, 1\}[/math]

  • Eigenwertdichte von 10 Millionen [math]10 \times 10[/math] Tridiagonalmatrizen mit Einträgen aus der Menge [math]\{-π, π\}[/math]

Feste Matrix mit kontinuierlicher Verteilung in bestimmten Werten (Eigenfish)

Hier wurden Matrizen von der Form [math]\,\begin{pmatrix} 0 & 0 & 0 & A \\ -1 & -1 & 0 & 0 \\ B & 0 & 0 & 0 \\ -1 & 1 & 1 & -1 \end{pmatrix}\,[/math] verwendet. Die Einträge A und B wurden dabei zufällig (gleichverteilt) aus einem kontinuierlichen Intervall ausgewählt.

Kleine Änderungen an den Einträgen der Matrix können dabei vollkommen unterschiedliche Formen hervorbringen. Für die Bilder wurde die obige Matrix teilweise leicht verändert und es wurden unterschiedliche Intervallgrenzen ausgewählt.

  • Eigenwertdichte von 3 Millionen Matrizen

  • Eigenwertdichte von 3 Millionen Matrizen

  • Animation von Matrizen mit [math]A,B \in [-\pi(1+i),\pi(1+i)][/math], wobei der Imaginärteil der unteren Grenze im Laufe der Animation bis auf [math]20i[/math] erhöht wurde.

Einzelnachweise und Quellen

  1. ↑ Anderson, G.W., Guionnet, A. und Zeitouni, O., "An introduction to random matrices" (2010), Cambridge University Press, Cambridge, isbn:978-0-521-19452-5
  2. ↑ 2,0 2,1 Mehta, M.L., "Random Matrices" (2004), Elsevier/Academic Press, Amsterdam. isbn:0-12-088409-7
  3. ↑ Zhenyu Liao. A random matrix framework for large dimensional machine learning and neural networks. Other. Université Paris-Saclay, 2019. English. NNT: 2019SACLC068. HAL-Id: tel-02397287
  4. ↑ Antonia M. Tulino, Sergio Verdú: Random Matrix Theory and Wireless Communications. Now, 2004.
  5. ↑ http://web.mit.edu/sea06/agenda/talks/Harding.pdf
  6. ↑ 6,0 6,1 https://de.linkfang.org/wiki/Zufallsmatrix
  7. ↑ Keating, Jon, "The Riemann zeta-function and quantum chaology", Proc. Internat. School of Phys. Enrico Fermi (1993) CXIX, 145–185, doi:10.1016/b978-0-444-81588-0.50008-0, isbn:9780444815880
  8. ↑ https://de.wikipedia.org/wiki/Bildrauschen
  9. ↑ VS Rychkov, S Borlenghi, H Jaffres, A Fert, X Waintal: Spin Torque and Waviness in Magnetic Multilayers: A Bridge Between Valet-Fert Theory and Quantum Approaches. In: Phys. Rev. Lett.. 103, Nr. 6, August 2009, S. 066602. doi:10.1103/PhysRevLett.103.066602 . PMID 19792592.
  10. ↑ DJE Callaway: Random Matrices, Fractional Statistics, and the Quantum Hall Effect. In: Phys. Rev., B Condens. Matter. 43, Nr. 10, April 1991, S. 8641–8643. doi:10.1103/PhysRevB.43.8641 . PMID 9996505.
  11. ↑ SR Bahcall: Random Matrix Model for Superconductors in a Magnetic Field. In: Phys. Rev. Lett.. 77, Nr. 26, Dezember 1996, S. 5276–5279. doi:10.1103/PhysRevLett.77.5276 . PMID 10062760.
  12. ↑ DM Zumbühl, JB Miller, CM Marcus, K Campman, AC Gossard: Spin-orbit Coupling, Antilocalization, and Parallel Magnetic Fields in Quantum Dots. In: Phys. Rev. Lett.. 89, Nr. 27, Dezember 2002, S. 276803. doi:10.1103/PhysRevLett.89.276803 . PMID 12513231.
  13. ↑ F Franchini, VE Kravtsov: Horizon in Random Matrix Theory, the Hawking Radiation, and Flow of Cold Atoms. In: Phys. Rev. Lett.. 103, Nr. 16, Oktober 2009, S. 166401. doi:10.1103/PhysRevLett.103.166401 . PMID 19905710.
  14. ↑ Wigner, E."Characteristic vectors of bordered matrices with infinite dimensions", Annals of Mathematics (1955) 62, 548–564, doi:10.2307/1970079, jstor:1970079
  15. ↑ T. Guhr, A. Müller–Groeling und H. A. Weidenmüller. Random-matrix theories in quantum physics: common concepts. Physics Reports,299, 189–425, 1998.
  16. ↑ https://www.bohemianmatrices.com
  17. ↑ https://ir.lib.uwo.ca/etd/6069/

letzter Zugriff für alle: 13.04.2021

Autoren

Silas Janke, Lea Homann, Daniel Gáspár, Falk Loewner

Abgerufen von „https://funfacts.mathi.uni-heidelberg.de/index.php?title=Zufallsmatrizen_-_Bohemians_und_die_geheimnisvolle_Ordnung_im_Chaos&oldid=3788“