Zauberwürfel: Unterschied zwischen den Versionen
AFaber (Diskussion | Beiträge) |
|||
| (50 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | |||
Der Zauberwürfel ist ein Drehpuzzle in Würfelform. Durch ihn kann man sich die Symmetrische Gruppe anschaulich vorstellen und mit ihrer Hilfe Aussagen über die Lösbarkeit des Würfels treffen. | Der Zauberwürfel ist ein Drehpuzzle in Würfelform. Durch ihn kann man sich die Symmetrische Gruppe anschaulich vorstellen und mit ihrer Hilfe Aussagen über die Lösbarkeit des Würfels treffen. | ||
| Zeile 253: | Zeile 254: | ||
** <math>8</math> Eckcubies | ** <math>8</math> Eckcubies | ||
* <math>6</math> verdrehbare Seiten, <math>21</math> verdrehbare Cubies | * <math>6</math> verdrehbare Seiten, <math>21</math> verdrehbare Cubies | ||
| − | <math>\Rightarrow 43x10^{18}</math> Möglichkeiten den Würfel zu verdrehen | + | <math>\Rightarrow 43x10^{18}</math> Möglichkeiten den Würfel zu verdrehen -> siehe [[Zauberwürfel#Orientierung|Orientierung]] (Formel in letzter Zeile des Abschnittes) |
| + | |||
| + | ==<big></big> Züge== | ||
| + | <table style="text-align: center; vertical-align: middle;" border="1"> | ||
| + | <tr> | ||
| + | <th>Zug</th><th>Eckenpermutation</th><th>Kantenpermutation</th><th>Eckenorientierung</th><th>Kantenorientierung</th> | ||
| + | </tr> | ||
| + | <tr><td>U</td><td>(1 4 3 2)</td><td>(E H G F)</td><td>0</td><td>(0,0,0,0,1,1,1,1,0,0,0,0)</td></tr> | ||
| + | <tr><td>F</td><td>(1 2 6 5)</td><td>(A E B I)</td><td>(1,2,0,0,2,1,0,0)</td><td>(1,1,0,0,1,0,0,0,1,0,0,0)</td></tr> | ||
| + | <tr><td>R</td><td>(2 3 7 6)</td><td>(B F C J)</td><td>(0,1,2,0,0,2,1,0)</td><td>(0,1,1,0,0,1,0,0,0,1,0,0)</td></tr> | ||
| + | <tr><td>L</td><td>(1 5 8 4)</td><td>(A L D H)</td><td>(2,0,0,1,1,0,0,2)</td><td>(1,0,0,1,0,0,0,1,0,0,0,1)</td></tr> | ||
| + | <tr><td>B</td><td>(3 4 8 7)</td><td>(C G D K)</td><td>(0,0,1,2,0,0,2,1)</td><td>(0,0,1,1,0,0,1,0,0,0,1,0)</td></tr> | ||
| + | <tr><td>D</td><td>(5 6 7 8)</td><td>(I J K L)</td><td>0</td><td>(0,0,0,0,0,0,0,0,1,1,1,1)</td></tr> | ||
| + | </table> | ||
==<big></big> Lösbarkeit== | ==<big></big> Lösbarkeit== | ||
| Zeile 266: | Zeile 280: | ||
<h5>"<math>\Rightarrow</math>"</h5> | <h5>"<math>\Rightarrow</math>"</h5> | ||
| − | Ein lösbarer Würfel muss aus "legalen" Zügen enstanden sein. Wenn man sich die Liste der Züge | + | Ein lösbarer Würfel muss aus "legalen" Zügen enstanden sein. Wenn man sich die Liste der [[Zauberwürfel#Züge|Züge]] |
| − | Also folgt, dass auch für jede Kombination von Zügen die Bedingung der Lösbarkeit | + | anschaut, sieht man, dass für jeden Zug die Bedingung <math> \left( sgn(\rho)=sgn(\sigma)\wedge \sum_{i=1}^8 x_i = 0\wedge \sum_{i=1}^{12} y_i = 0 \right) </math> wahr ist. |
| + | |||
| + | Also folgt, dass auch für jede Kombination von Zügen die Bedingung der Lösbarkeit wahr ist. | ||
<h5>"<math>\Leftarrow</math>"</h5> | <h5>"<math>\Leftarrow</math>"</h5> | ||
| + | '''In Bearbeitung''' | ||
| + | <!-- | ||
Beweis durch Kontraposition, also <math> \neg \left( sgn(\rho)=sgn(\sigma)\wedge \sum_{i=1}^8 x_i = 0\wedge \sum_{i=1}^{12} y_i = 0 \right) \Rightarrow </math> Der Würfel ist nicht Lösbar. | Beweis durch Kontraposition, also <math> \neg \left( sgn(\rho)=sgn(\sigma)\wedge \sum_{i=1}^8 x_i = 0\wedge \sum_{i=1}^{12} y_i = 0 \right) \Rightarrow </math> Der Würfel ist nicht Lösbar. | ||
Wenn die Bedingung nicht erfüllt ist, kann man durch Züge die Bedingung nicht wieder erfüllen, da jeder Zug wie schon erwähnt, die Summe der Orientierung bzw. die Gleichheit der Permutations-Signums nicht ändert. Da aber ein gelößter Würfel genau diese Bedingung erfüllt kann man ihn nicht lösen. | Wenn die Bedingung nicht erfüllt ist, kann man durch Züge die Bedingung nicht wieder erfüllen, da jeder Zug wie schon erwähnt, die Summe der Orientierung bzw. die Gleichheit der Permutations-Signums nicht ändert. Da aber ein gelößter Würfel genau diese Bedingung erfüllt kann man ihn nicht lösen. | ||
| − | + | --> | |
==<big></big> Lösungsstrategie== | ==<big></big> Lösungsstrategie== | ||
<h4> Alternative Lösungsstrategie</h4> | <h4> Alternative Lösungsstrategie</h4> | ||
Eine alternative Lösungsstrategie wäre den Würfel einem Affen zu geben, der zufällige Züge ausführt, bis der Würfel gelöst ist. Diese Strategie führt bei jeder Variation, egal ob 2x2, Tetraedar oder Dodekaeder etc. zu einer Lösung, ist aber ineffektiv, weshalb hier eine bessere Methode vorgestellt wird. | Eine alternative Lösungsstrategie wäre den Würfel einem Affen zu geben, der zufällige Züge ausführt, bis der Würfel gelöst ist. Diese Strategie führt bei jeder Variation, egal ob 2x2, Tetraedar oder Dodekaeder etc. zu einer Lösung, ist aber ineffektiv, weshalb hier eine bessere Methode vorgestellt wird. | ||
| − | Wir betrachten den unter | + | Wir betrachten den unter [[Zauberwürfel#Notation|Notation]] definierten Würfel. |
====<big></big> Obere Ebene==== | ====<big></big> Obere Ebene==== | ||
Man beginnt mit dem Lösen der weißen Kanten, indem man das sogenannte "weiße Kreuz" intuitiv bildet. Dabei muss darauf geachtet werden, dass die zweite Farbe der Kanten mit dem mittleren Stein der mittleren Seite übereinstimmt. | Man beginnt mit dem Lösen der weißen Kanten, indem man das sogenannte "weiße Kreuz" intuitiv bildet. Dabei muss darauf geachtet werden, dass die zweite Farbe der Kanten mit dem mittleren Stein der mittleren Seite übereinstimmt. | ||
| Zeile 326: | Zeile 344: | ||
* <math>4</math> kleine cubies/Eckcubies | * <math>4</math> kleine cubies/Eckcubies | ||
* <math>6</math> verdrehbare Seiten, alle cubies verdrehbar | * <math>6</math> verdrehbare Seiten, alle cubies verdrehbar | ||
| − | <math>\Rightarrow 3^·674^·160</math> Möglichkeiten den Würfel zu verdrehen | + | <math>\Rightarrow 3^·674^·160</math> Möglichkeiten den Würfel zu verdrehen (<math>=\frac{8!\cdot 3^8}{3\cdot 6\cdot 4}</math> Wobei die Berechnung im Nenner wie beim <math>3x3</math>-Würfel für die möglichen Positionen der <math>8</math> Ecken und deren Orientierungsmöglichkeiten steht -> siehe [[Zauberwürfel#Orientierung|Ordnung]] (Formel in letzter Zeile des Abschnittes), und der Zähler für die Anzahl der Seiten, der Cubies einer Seite und deren Orientierungsmöglichkeit) |
===<big></big> Lösungsstrategie=== | ===<big></big> Lösungsstrategie=== | ||
| Zeile 335: | Zeile 353: | ||
:<math> L^2 </math> <math> B^2 </math> <math> L′ </math> <math> F′ </math> <math> L </math> <math> B^2 </math> <math> L′ </math> <math> F </math> <math> L′ </math> | :<math> L^2 </math> <math> B^2 </math> <math> L′ </math> <math> F′ </math> <math> L </math> <math> B^2 </math> <math> L′ </math> <math> F </math> <math> L′ </math> | ||
In Permutationsschreibweise gilt: | In Permutationsschreibweise gilt: | ||
| − | Der Würfel wird erstmal um <math>C_U^2</math>, (<math>2</math> | + | Der Würfel wird erstmal um <math>C_U^2</math>, (<math>2</math> Obere-Umdrehungen um die eigene Achse) gedreht, um so die zu lösende Fläche oben zu haben. Die Permutationsschreibweise wird von hinten nach vorne angewendet somit wird der Algorithmus von hinten nach vorne geschrieben und die einzelnen Drehungen in Permutations-Schreibweise übersetzt, dies sieht folgender Massen aus: |
:<math> L′ </math> <math> F </math> <math> L′ </math> <math> B^2 </math> <math> L </math> <math> F′ </math> <math> L′ </math> <math> B^2 </math> <math> L^2 </math> | :<math> L′ </math> <math> F </math> <math> L′ </math> <math> B^2 </math> <math> L </math> <math> F′ </math> <math> L′ </math> <math> B^2 </math> <math> L^2 </math> | ||
:<math> (1 4 8 5) </math> <math> (1 2 6 5) </math> <math> (1 4 8 5) </math> <math> (3 4 8 7) </math> <math> (3 4 8 7) </math> <math> (1 5 8 4) </math> <math> (1 5 6 2) </math> <math> (1 4 8 5) </math> <math> (3 4 8 7) </math> <math> (3 4 8 7) </math> <math> (1 5 8 4) </math> <math> (1 5 8 4) </math> | :<math> (1 4 8 5) </math> <math> (1 2 6 5) </math> <math> (1 4 8 5) </math> <math> (3 4 8 7) </math> <math> (3 4 8 7) </math> <math> (1 5 8 4) </math> <math> (1 5 6 2) </math> <math> (1 4 8 5) </math> <math> (3 4 8 7) </math> <math> (3 4 8 7) </math> <math> (1 5 8 4) </math> <math> (1 5 8 4) </math> | ||
| Zeile 358: | Zeile 376: | ||
==<big></big>Megaminx== | ==<big></big>Megaminx== | ||
<h4>Eigenschaften</h4> | <h4>Eigenschaften</h4> | ||
| − | Der Megaminx ist ein Dodekaeder und besteht so aus | + | Der Megaminx<ref>https://de.wikipedia.org/wiki/Megaminx</ref> ist ein Dodekaeder und besteht so aus |
<ul> | <ul> | ||
<li>12 Flächen (Daher 12 unbewegliche Mittelsteine)</li> | <li>12 Flächen (Daher 12 unbewegliche Mittelsteine)</li> | ||
| Zeile 364: | Zeile 382: | ||
<li>30 Kantensteinen</li> | <li>30 Kantensteinen</li> | ||
</ul> | </ul> | ||
| − | |||
| − | + | Also vergleichsweise zur [[Zauberwürfel#Ordnung|Ordnung]] des 3x3 <math>(\rho, \sigma, x, y) \in S_{20} \times S_{30} \times (\mathbb{Z} / 3\mathbb{Z})^{20} \times (\mathbb{Z} / 2\mathbb{Z})^{30} </math> | |
| + | |||
| + | Daher gibt es nicht <math> 30!\cdot 2^{30}\cdot 20! \cdot 3^{20}</math> mögliche Verdrehungen eines Megaminx, sondern <math>\frac{1}{12} \cdot 30!\cdot 2^{30}\cdot 20! \cdot 3^{20} \approx | ||
10^{68}</math>. | 10^{68}</math>. | ||
| Zeile 378: | Zeile 397: | ||
Zünachst löst man intuitiv einen Stern, so ähnlich wie man beim 3x3 zuerst ein Kreuz löst. (Bild) | Zünachst löst man intuitiv einen Stern, so ähnlich wie man beim 3x3 zuerst ein Kreuz löst. (Bild) | ||
| − | Danach die Ecken des Sterns, der Algorhitmus ist der selbe, jedoch bezeichnet hier R U und L andere Flächen. (Bild | + | Danach die Ecken des Sterns, der Algorhitmus ist der selbe, jedoch bezeichnet hier <math>R</math><math>U</math>und <math>L</math> andere Flächen. (Bild |
Dann die zweite Reihe, wieder mit dem selben Algorhitmus und Flächen wie zuvor. | Dann die zweite Reihe, wieder mit dem selben Algorhitmus und Flächen wie zuvor. | ||
| − | Danach löst man die darüber liegenden Kanten, dieser Schritt ist intuitiv lösbar. Da | + | Danach löst man die darüber liegenden Kanten, dieser Schritt ist intuitiv lösbar. Da viele Fläschen noch nicht gelöst sind und man die daher frei bewegen kann. |
| − | Um die anliegenden Kanten zu lösen, positioniert man den passenden Stein über dem Mittelstein und führt den Algorhitmus F' R' F' F' R F bzw. F L F F L' F' aus. | + | Um die anliegenden Kanten zu lösen, positioniert man den passenden Stein über dem Mittelstein und führt den Algorhitmus <math>F'</math> <math> R'</math> <math> F'</math> <math> F'</math> <math> R</math> <math> F</math> bzw.<math> F</math> <math> L</math> <math> F</math> <math> F </math> <math>L' </math> <math>F' </math> aus. |
Die nächsten Ecken und Kanten sind gleichzusetzen mit den ersten Ecken und Kanten des 3x3. Man hat noch eine komplette Fläsche zum lösen frei, genauso wie beim 3x3. | Die nächsten Ecken und Kanten sind gleichzusetzen mit den ersten Ecken und Kanten des 3x3. Man hat noch eine komplette Fläsche zum lösen frei, genauso wie beim 3x3. | ||
| − | Nun formt man das letzte Kreuz. Zunächst die Orientierung der Kanten mit F U R U' R' F' entweder muss man diesen Algorhitmus ein mal (Drei Ecken ist richtig orientiert) oder zwei mal (Eine Ecken sind richtig orientiert) ausführen. | + | Nun formt man das letzte Kreuz. Zunächst die Orientierung der Kanten mit <math>F </math> <math>U</math> <math> R </math> <math>U' </math> <math>R' </math> <math>F' </math> entweder muss man diesen Algorhitmus ein mal (Drei Ecken ist richtig orientiert) oder zwei mal (Eine Ecken sind richtig orientiert) ausführen. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Um nun die Kanten an die Richtige position zu bringen führt man den Algorhitmus <math>R </math> <math>U </math> <math>U </math> <math>R' </math> <math>U' </math> <math>R </math> <math>U' </math> <math>R' </math> aus. Eventuell muss man diesen mehrfach ausführen. | ||
| + | Die Ecken an die richtige Position zu bringen ist wie beim 3x3 nur muss man hier 2 mal U ausführen. Also <math> R </math> <math>U </math> <math>U </math> <math>R' </math> <math>U' </math> <math>U' </math><math>L' </math> <math>U</math> <math> U </math> <math>R </math> <math>U' </math> <math>U' </math> <math>R' </math> <math>L</math> | ||
| − | < | + | Um die Ecken nun richtig zu orientieren führt man wie beim 3x3 den Algorhitmus <math>R' </math> <math>D' </math> <math>R </math> <math>D </math> aus bist die Ecke stimmt und dann dreht man die Nächste Ecke auf die Position der ersten und führt den Algorhitmus aus usw. bis alle Ecken gelößt sind. |
=<big></big> Quellen= | =<big></big> Quellen= | ||
Aktuelle Version vom 27. April 2021, 06:41 Uhr
Der Zauberwürfel ist ein Drehpuzzle in Würfelform. Durch ihn kann man sich die Symmetrische Gruppe anschaulich vorstellen und mit ihrer Hilfe Aussagen über die Lösbarkeit des Würfels treffen.
Symmetrische Gruppe
Die Symmetrische Gruppe [math]S_n[/math] ist die Gruppe, die aus allen Permutationen (Vertauschungen) einer [math] n [/math]-elementigen Menge besteht. Man bezeichnet [math] n \in ℕ [/math] den Grad der Gruppe (Anzahl der Elemente).
Die Gruppenoperation in der symmetrischen Gruppe ist die Komposition (Hintereinanderausführung) der Permutationen.
Das neutrale Element der Gruppe ist die Identitätsabbildung, welche bewirkt, dass keine Permutation stattfindet.
Die symmetrische Gruppe [math]S_n[/math] ist endlich und besitzt die Ordnung [math]n![/math].
Für Grad [math]n\gt 2[/math] ist die [math]S_n[/math] nichtabelsch. [1]
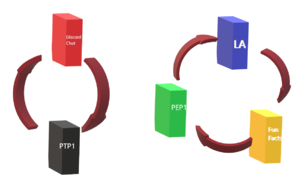
Zur Veranschaulichung folgt ein Beispiel anhand eines Bücherregals:
Zunächst führen wir die Anfangsaufstellung der Bücher ein. Hierbei beschreibt 1 = "LA" , 2 = "Fun Facts" , 3 = "Discord Chat" , 4 = "PTP1" , 5 = "PEP1"
Als nächstes wird die Permutation [math] \sigma [/math] auf die Aufstellung angewandt, wobei
- [math] σ = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 2 & 3 & 1 & 4 & 5 \end{pmatrix} [/math].
Zur Notation der Zweizeilenform: In der ausführlichen Darstellung einer [math] n [/math]-stelligen Permutation [math] \pi [/math] schreibt man diese als Matrix mit zwei Zeilen und [math] n [/math] Spalten. In der oberen Zeile stehen die Zahlen von [math] 1 [/math] bis [math] n [/math] (in beliebiger Reihenfolge). Unter jeder Zahl [math] j\in \{1,...,n\} [/math] steht dann in der zweiten Zeile der Funktionswert [math] \pi(j)[/math] :
[math] \pi = \begin{pmatrix} 1 & 2 & 3 & ... & n \\ \pi(1) & \pi(2) & \pi(3) & ... & \pi(n) \end{pmatrix} [/math]
Auch in der zweiten Zeile steht somit jede Zahl von [math] 1 [/math] bis [math] n [/math] genau einmal.
Sei [math] \mu [/math] eine andere Permutation.
Zuletzt wird [math] \mu [/math] auf die bereits von [math] \sigma [/math] permutierte Aufstellung angewandt. Hieraus ergibt sich für die Endaufstellung = [math] \sigma \circ \mu [/math]
- [math] μ = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 4 & 3 & 5 & 1 & 2 \end{pmatrix} [/math]
Zykelschreibweise
Die Vertauschungen werden häufig in sogenannten "Zykeln" geschrieben. Dabei werden die Positionen die durch die Vertauschungen geändert werden hintereinander in eine Klammer geschrieben. Dementsprechend ist die Zykelschreibweise nicht eindeutig. Die klassische Notation ist in der Klammer aufsteigend.
Die Zykelschreibweise von [math]\sigma[/math] wäre zum Beispiel:
- [math] \sigma = ( 1 ~ 2 ~ 3) (4) (5) = ( 1 ~ 2 ~ 3) [/math]
Dabei werden in der Notation die Zyklen der Länge 1 nicht mitgeschrieben.
Analog zu oben wäre die Schreibweise zu [math]\mu[/math] :
- [math] \mu = ( 1 ~ 4) (2 ~3 ~ 5)[/math]
Zu beachten ist hierbei, dass die Permutationen im Generellen nicht kommutieren:
- [math] \sigma \circ \mu = ( 1 ~ 2 ~ 3) ( 1 ~ 4) (2 ~3 ~ 5)= (1 ~ 4 ~ 2)(3~5) [/math]
- [math] \mu \circ \sigma = ( 1 ~ 4) (2 ~3 ~ 5)( 1 ~ 2 ~ 3)= (1 ~ 3 ~ 4)(2~5) [/math]
- [math]\mapsto \sigma \circ \mu \neq \mu \circ \sigma [/math]
Nice to know: Disjunkte Zykel kommutieren
Signumsabbildung
Die Signumsabbildung ist eine surjektive Abbildung welche eine beliebige Permutation auf [math] 1 [/math] oder [math] -1 [/math] abbildet. Dabei kann man die [math] 1 [/math] so interpretieren, dass die abgebildete Permutation eine gerade Anzahl von Fehlstellen hat. Die [math] -1 [/math] zeigt somit eine ungerade Anzahl von Fehlstellen an.
Als Fehlstelle versteht man in diesem Kontext, dass ein Element welches vorher hinter einem anderen Element platziert war, durch die Permutation vor das andere Element gezogen wurde. Ein Beispiel für eine Permutation mit zwei Fehlstellen wäre:
- [math] \mu = ( 1 ~ 2 ~ 3) \longrightarrow sgn(\mu) = +1 [/math]
In diesem Beispiel entsteht die Fehlstelle dadurch, dass die [math] 3 [/math] "vor" die [math] 1 [/math] und [math] 2 [/math] geschoben wird.
Für eine generelle Berechnung der Fehlstellen für [math] \pi \in S_n [/math] kann die Formel:
- [math]sgn(\pi) = \prod_{1 \leq i\lt j \leq n} \frac{\pi(j)-\pi(i)}{j-i}[/math]
genutzt werden.[2]
Die Abbildung : [math]sgn: S_n \mapsto \{ \pm 1 \}[/math] ist dabei ein Gruppenhomomorphismus.
Alternierende Gruppe
Die alternierende Gruppe vom Grad [math]n[/math] ist eine Untergruppe der symmetrischen Gruppe [math]S_n[/math]. Sie besteht aus allen gerad-anzahligen Permutationen einer [math]n[/math]-elementigen Menge.
Sie ist definiert als:
[math]A_n[/math] := [math]\{\sigma \in S_n |sgn(\sigma)=1\} \subset S_n [/math].
Die Verknüpfung der alternierenden Gruppe ist, wie auch die der symmetrischen Gruppe, die Verkettung (Hintereinanderausführung) der Permutationen.
Lemma: [math]A_n[/math] wird erzeugt von Zykeln der Form [math](12i)[/math] mit [math]i \in \{3,...,n\}[/math] mit [math]n \geq 3[/math].
D.h. für jedes [math]\sigma \in A_n[/math] gibt es eine Darstellung [math]\sigma = (12i_1)(12i_2)...(12i_k)[/math] mit [math]i_1 ...i_k \in \{3,...,k\}[/math].
Anwendung auf den Zauberwürfel
Notation
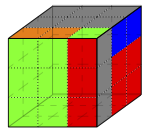
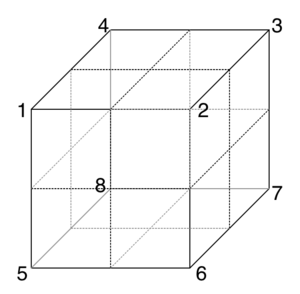
Aussehen & Beschriftung des Würfels
Die einzelnen kleinen Würfel eines großen Würfels werden als Cubies bezeichnet. Für die Beschriftung des Würfels nummeriert man die Eckcubies mit den Zahlen [math] 1 [/math] bis [math] 8 [/math] durch und benennt jede Kante mit einem Buchstaben [math] A [/math] bis [math] L [/math].
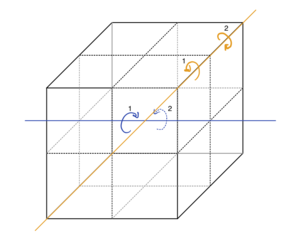
Die Seiten des Würfels werden mit grossen Buchstaben, [math] F [/math](Front), [math] B [/math](Back), [math] U [/math](Up), [math] D [/math](Down), [math] R [/math](Right), [math] L [/math](Left) bezeichnet, wobei wir im Ausgangszustand zur Vereinfachung die Seiten farblich folgendermaßen definieren: [math] F [/math](grün), [math] B [/math](blaue), [math] U [/math](weiss), [math] D [/math](gelb), [math] R [/math](orange), [math] L [/math](rot). Diese Buchstaben stehen ausserdem für eine Umdrehung der jeweiligen Seite im Uhrzeigersinn. Eine Umdrehung gegen den Uhrzeigersinn wird mit [math] F' [/math], [math] B' [/math], [math] U' [/math], [math] D' [/math], [math] R' [/math], [math] L' [/math] bezeichnet. Umdrehungen des Würfels um die Eigene Achse werden mit [math] C [/math] beschrieben: [math] C_U [/math] Umdrehung nach oben um die eigene Achse nun liegt die grüne Seite oben), [math] C_D[/math](nach unten), [math] C_L [/math] (nach links), [math] C_R [/math] (nach rechts). [math] C_U^2 [/math][math] (=C_D^2 [/math]) entspricht einer zweifachen Umdrehung um die eigene Achse nach oben.
Bemerkung
Die eigene Achse bei [math] C_U [/math] und [math] C_D [/math] Umdrehung ist als horizontale Achse von der "[math] L [/math]" zur "[math] R [/math]" Seite des Würfels zu verstehen.
Die eigene Achse bei [math] C_R [/math] und [math] C_L [/math] Umdrehungen ist als horizontale Achse von der "[math] F [/math]" zur "[math] B [/math]" Seite des Würfels zu verstehen.
[math] C_U^D[/math] = [math] C_U^′ [/math] entspricht einer Rückwärtsdrehung.
Drehungen einer Scheibe in Permutations-Schreibweise
Eine Umdrehung einer Ebene(Seite) des Würfels entspricht einem Zykel/Permutation in [math]S_8[/math] für die Ecken und in [math]S_{12}[/math] für die Kanten. Eine Zugfolge (mehrere Umdrehungen einer/verschiedener Ebenen) wird in Permutations-Schreibweise geschrieben. Die Permutationschreibweise, wird "mathematisch", d.h. von rechts nach vorne gelesen.
Beispiele
Für die Ecken gilt beispielsweise:
- [math] U = (1 4 3 2) [/math]
- [math] F = (1 2 6 5) [/math]
Für die Kanten gilt beispielsweise:
- [math] U = (E H G F) [/math]
- [math] F = (A E B I) [/math]
Für eine Zugfolge gilt beispielsweise:
- [math] FU = (1 2 6 5)(1 4 3 2) = (1 4 3 6 5) [/math] (Erst obere(up) Umdrehung, dann vordere(front) Umdrehung)
Nach dieser Zugfolge liegt an Position 2 wieder die Ursprungsecke, nun aber einmal im Uhrzeigersinn verdreht.
Gruppeneigenschaften
Sowohl bei der Betrachtung der Würfelecken, als auch der Würfelkanten stellt, jede Drehung (jeweils im mathematisch negativen Sinn) einer der Würfelscheiben eine zyklische Permutation dar, die als Element der symmetrischen Gruppe [math]S_8[/math] (für die Permutionen der Eckwürfelchen), oder [math]S_{12}[/math] (für die Permutationen der Kanten), aufgefasst werden kann. Jede mögliche Würfeldrehung ist dabei als Zusammensetzung von Verknüpfungen der genannten sechs Grundpermutationen [math]\{F,B,R,L,U,D\}[/math] darstellbar.[4]
Sei [math]G[/math] die Menge aller möglichen Drehoperationen am Zauberwürfel. Mit der Verknüpfung "[math]\circ[/math]"[math]: G \times G \rightarrow G [/math] wird [math]G[/math] eine Gruppe:
- Die Abgeschlossenheit durch die Verknüpfung "[math]\circ[/math]" der Gruppenelemente ist gegeben.
- Da auf Elemente aus [math]S_n, n \in \{8,12\}[/math] zurückgegriffen wird, gilt das Assoziativgesetz.
- Das neutrale Element [math]e_n, n \in \{8,12\}[/math] ist die Nulloperation, also das Nicht-Verdrehen des Würfels, sodass gilt: [math]\forall g \in G: g \circ e_n = e_n \circ g =g [/math]
- Es existiert ein eindeutiges Inverses [math]g^{-1}[/math]zu jedem [math] g \in G : g \circ g^{-1} = g^{-1} \circ g = e_n [/math]. Für die Grundpermutationen ist dies anschaulich jeweils die Rückdrehung im mathematischen Uhrzeigersinn.
Die Gruppe [math]G[/math] ist nicht abelsch; so ist beispielsweise [math]F \circ L \neq L \circ F [/math].
Ordnung
Die Ordnung der Gruppe G ergibt sich aus der Anzahl [math]\vert G \vert[/math] der möglichen Drehoperationen. Zu deren Bestimmung ist die natürliche Bijektion zwischen der Gruppe [math]G[/math] und der Menge aller möglichen, durch ein [math]g \in G[/math] erreichten, Würfelpositionen nützlich:
Die Würfelposition kann eindeutig durch den Positionsvektor [math](\rho, \sigma, x, y) \in S_8 \times S_{12} \times (\mathbb{Z} / 3\mathbb{Z})^8 \times (\mathbb{Z} / 2\mathbb{Z})^{12} [/math] dargestellt werden. Dabei zeigt [math]\rho \in S_8[/math] die Permutation der Eckwürfelchen, [math]\sigma \in S_{12} [/math] die Permutation der Kanten, [math]x \in (\mathbb{Z} / 3\mathbb{Z})^8[/math] die Orientierung der Eckwürfelchen und [math]y \in (\mathbb{Z} / 2\mathbb{Z})^{12} [/math]die Orientierung der Kanten, jeweils ausgehend von der Grundstellung, an. [5]
Orientierung
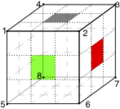
Die angesprochenen Orientierungen sind dabei folgendermaßen definiert:
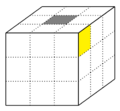
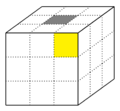
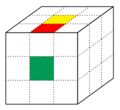
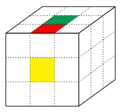
Für die Orientierung der Ecken wird die Tatsache verwendet, dass jeder Eckwürfel genau eine gelbe oder weiße Seite hat. Ist diese Seite auf der Deckenfläche (diese wird so gewählt, dass sich eine weiße oder gelbe Teilfläche (im Bild als grau dargestellt) auf der mittleren Position befindet) positioniert, so wird der Orientierung die Äquivalenzklasse der [math][0][/math] zugeordnet. Ist sie von dort aus entgegen des mathematischen Sinns zur Seite gedreht, wird ihr die [math][1][/math] zugeordnet, und ist sie von dort aus, aus Sicht der angrenzenden Seitenfläche, im mathematischen Sinn nach vorne gedreht, die [math][2][/math]. Wird dies für jedes der acht Eckwürfelchen [math]x_i, i \in \{1, \ldots, 8\}[/math]durchgeführt, erhält man den Orientierungsvektor [math]x=(x_1, \ldots, x_8) \in (\mathbb{Z} / 3\mathbb{Z})^8 [/math]. Dies wird an den folgenden Abbildungen ersichtlich:
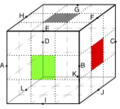
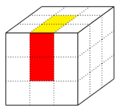
Für die Orientierung der Kanten verwendet man, dass jede Kante zwei Farben aus zwei verschiedenen Farbgruppen [math]([/math]diese sind gelb/weiß [math](ge/w)[/math], grün/blau ([math](gr/b)[/math], rot/orange [math](r/o))[/math] besitzt. Stellt man die Farbauswahl schematisch als [math](ge / w \,\,\,\, gr / b \,\,\,\, r / o\,\,\,\, ge / w \,\,\,\, gr / b)[/math] dar, so kann man eine Auswahl für die beiden möglichen Orientierungen der Kante wie folgt treffen: Man vergleicht jeweils die Farben der Mittelwürfelchen und der direkt aufeinandertreffenden Seitenwürfelchen der Zauberwürfelseiten, zwischen denen die gewünschte Kante liegt. Anschließend bestimmt man, je für die beiden Mittelwürfelchen und dann für die Seitenwürfelchen, in welcher Richtung die dargebotene Farbe des Vorderseitenwürfels aus der des Oberseitenwürfels aus dem Schema [math](ge / w \,\,\,\, gr / b \,\,\,\, r / o\,\,\,\, ge / w \,\,\,\, gr / b)[/math] hervorgeht, also ob die Folgerichtung rechts oder links ist. Stimmen die Richtungen auf den Feldern derselben Zauberwürfelseite überein, so entspricht die Kantenorientierung der Äquivalenzklasse der [math][0][/math], ansonsten der der [math][1][/math]. Dies wird anhand der folgenden Beispiele verdeutlicht:
Die Ordnung von [math]G[/math] ergibt sich nun aus der Anzahl der möglichen Positionen der Eckwürfel, der Kantenwürfel, sowie der möglichen Orientierungen der Ecken und Kanten und den Aspekten des Lösbarkeitssatzes als
[math]\vert G \vert = \frac{8!\cdot 12!\cdot 3^8\cdot 2^{12}}{2 \cdot 2 \cdot3} = 43\,\,\, 252\,\,\, 003\,\,\, 274\,\,\, 489\,\,\, 856\,\,\, 000 [/math][6]
Mögliche Untergruppen
Eine recht einfache Oberkategorie möglicher Untergruppen am Zauberwürfel ist durch die sogenannten zyklischen Untergruppen gegeben. Das sind jene Untergruppen, die sich nur aus einem einzigen [math]g \in G [/math] und dessen Verknüpfungen zusammensetzten. Ein Beispiel hierfür ist etwa die Teilmenge der Drehungen der oberen Würfelscheibe entgegen des mathematisch negativen Sinnes [math]\{U\} \subset G [/math] mit der Verknüpfung "[math]\circ[/math]".
Das neutrale Element ist enthalten durch [math] e = U^4 \in (\{U\},\circ)[/math] und somit gilt auch [math] U \circ U^{-1}=e \in (\{U\},\circ) [/math].
Weitere Beispiele für Untergruppen sind die orientierungserhaltende Untergruppe [math] G_1 := \{g=(\rho, \sigma, x, y) \in G| x=0, y=0\} [/math]
und die, nur die Orientierung ändernde, Untergruppe [math] G_2 := \{g=(\rho, \sigma, x, y) \in G| \rho=1, \sigma=1\} [/math].[7]
Der 3x3 Zauberwürfel
Eigenschaften
Der klassische 3x3 Zauberwürfel besteht aus:
- [math]27[/math] kleinen cubies bestehend aus:
- [math]1[/math] Zentrumcubie
- [math]6[/math] mittleren cubies
- [math]12[/math] Kantencubies
- [math]8[/math] Eckcubies
- [math]6[/math] verdrehbare Seiten, [math]21[/math] verdrehbare Cubies
[math]\Rightarrow 43x10^{18}[/math] Möglichkeiten den Würfel zu verdrehen -> siehe Orientierung (Formel in letzter Zeile des Abschnittes)
Züge
| Zug | Eckenpermutation | Kantenpermutation | Eckenorientierung | Kantenorientierung |
|---|---|---|---|---|
| U | (1 4 3 2) | (E H G F) | 0 | (0,0,0,0,1,1,1,1,0,0,0,0) |
| F | (1 2 6 5) | (A E B I) | (1,2,0,0,2,1,0,0) | (1,1,0,0,1,0,0,0,1,0,0,0) |
| R | (2 3 7 6) | (B F C J) | (0,1,2,0,0,2,1,0) | (0,1,1,0,0,1,0,0,0,1,0,0) |
| L | (1 5 8 4) | (A L D H) | (2,0,0,1,1,0,0,2) | (1,0,0,1,0,0,0,1,0,0,0,1) |
| B | (3 4 8 7) | (C G D K) | (0,0,1,2,0,0,2,1) | (0,0,1,1,0,0,1,0,0,0,1,0) |
| D | (5 6 7 8) | (I J K L) | 0 | (0,0,0,0,0,0,0,0,1,1,1,1) |
Lösbarkeit
Behauptung
Ein Würfel ist genau dann lösbar, wenn:
- [math]sgn(\rho)=sgn(\sigma)[/math]
- [math]\sum_{i=1}^8 x_i = 0[/math]
- [math]\sum_{i=1}^{12} y_i = 0[/math]
Beweis
"[math]\Rightarrow[/math]"
Ein lösbarer Würfel muss aus "legalen" Zügen enstanden sein. Wenn man sich die Liste der Züge
anschaut, sieht man, dass für jeden Zug die Bedingung [math] \left( sgn(\rho)=sgn(\sigma)\wedge \sum_{i=1}^8 x_i = 0\wedge \sum_{i=1}^{12} y_i = 0 \right) [/math] wahr ist.
Also folgt, dass auch für jede Kombination von Zügen die Bedingung der Lösbarkeit wahr ist.
"[math]\Leftarrow[/math]"
In Bearbeitung
Lösungsstrategie
Alternative Lösungsstrategie
Eine alternative Lösungsstrategie wäre den Würfel einem Affen zu geben, der zufällige Züge ausführt, bis der Würfel gelöst ist. Diese Strategie führt bei jeder Variation, egal ob 2x2, Tetraedar oder Dodekaeder etc. zu einer Lösung, ist aber ineffektiv, weshalb hier eine bessere Methode vorgestellt wird.
Wir betrachten den unter Notation definierten Würfel.
Obere Ebene
Man beginnt mit dem Lösen der weißen Kanten, indem man das sogenannte "weiße Kreuz" intuitiv bildet. Dabei muss darauf geachtet werden, dass die zweite Farbe der Kanten mit dem mittleren Stein der mittleren Seite übereinstimmt.
Im Anschluss löst man die weißen Ecken, sodass die weiße Fläche vervollständigt wird. Dafür bringt man den passenden Stein für Position [math] 2 [/math] in Position [math] 6 [/math], indem man den Würfel, wenn er sich in der unteren Ebene befindet, mit Hilfe von [math] D [/math] beziehungsweise [math] D' [/math] dreht und wenn er sich in der oberen Ebene befindet, mit [math] R' [/math] [math] D' [/math] [math] R [/math] herunterholt, um auch dann [math] D [/math] bzw. [math] D'[/math] zu verwenden und benutzt im Anschluss den folgenden Algorithmus [math] O [/math] so oft, bis die jeweilige Ecke weiß ist: [math] R' [/math] [math] D' [/math] [math] R [/math] [math] D [/math]. Man bemerkt, dass dieser immer die übereinander liegenden Eckcubies in Position [math] 2 [/math] und [math] 6 [/math] tauscht, weshalb er drei oder sechs Mal hintereinander angewendet werden muss, damit Position und Orientierung stimmt.
Mittlere Ebene
Hierfür drehen wir die weiße Seite mit [math] C_U^2 [/math] nach unten. Nun hat man zwei Algorithmen, welche symmetrisch zueinander sind. Der Algorithmus [math] M_L [/math] [math] = [/math] [math] U' [/math] [math] L' [/math] [math] U [/math] [math] L [/math] [math] U [/math] [math] F [/math] [math] U' [/math] [math] F' [/math] bringt den Kantencubie [math] K [/math] an die Position [math] D [/math]. Die resultierende Eckenpermutation entspricht [math] (576) [/math] und die der Kanten [math] (D I L J K) [/math]. Beim [math] M_R [/math] [math] = [/math] [math] U [/math] [math] R [/math] [math] U' [/math] [math] R' [/math] [math] U' [/math] [math] F' [/math] [math] U [/math] [math] F [/math] Algorithmus bringt man den Kantencubie [math] K [/math] an die Stelle [math] C [/math]. Hierbei gilt für die Ecken [math] (568) [/math] und für die Kanten [math] (CIJLK)[/math]. Damit die Orientierung der Kanten passt, muss die Farbe der Kante in Position [math] K [/math] mit der Farbe auf der Seite [math] F [/math] übereinstimmen. Abhängig von der anderen Farbe in Position [math] K [/math] muss dann [math] M_L [/math] oder [math] M_R [/math] benutzt werden. Wenn keine Kante mit einer roten, orangenen, blauen oder grünen Fläche mehr an Position [math] I [/math], [math] J [/math], [math] K [/math] oder [math] L [/math] ist, muss diese aus der mittleren Ebene herausgeholt werden. Hierfür benutzt man einen der beiden Algorithmen, um dann die Kante nach dem gleichen Schema wieder einzufügen.
Untere Ebene
Die letzte Ebene wird gelöst, indem man zuerst ein gelbes Kreuz bildet. Dafür schauen wir uns den Würfel immer noch so an, dass die weiß Fläche unten ist. Den [math] U [/math] [math] = [/math] [math] F [/math] [math] R [/math] [math] U [/math] [math] R' [/math] [math] U' [/math] [math] F' [/math] Algorithmus führt man ein bis drei Mal aus, bis besagtes Kreuz entsteht. Die Kanten permutieren nach einer Anwendung nach [math] (IKJ) [/math], bei zwei Anwendungen nach [math] (IJK) [/math] und bei drei permutieren sie nicht.
Danach werden die Kanten getauscht, da die seitlichen Farben noch nicht übereinstimmen. Der [math] U_K [/math] [math] = [/math] [math] R [/math] [math] U [/math] [math] R' [/math] [math] U [/math] [math] R [/math] [math] U [/math] [math] U [/math] [math] R' [/math] [math] U [/math] Algorithmus muss manchmal zwei Mal ausgeführt werden, wenn die gegenüberliegende Kanten getauscht werden müssen, da er zum Tauschen von den zwei nebeneinander liegenden Kanten [math] K [/math] und [math] L [/math] verwendet wird, weshalb der Würfel dann mit [math] C_L [/math] bzw. [math] C_R [/math] in die richtige Position gedreht werden muss, um nochmal angewendet zu werden.
Zum Schluss müssen die Ecken an die richtige Position gebracht werden, um dann richtig orientiert zu werden. Dafür sucht man nach einer Ecke in der richtigen Position und hält sie vorne rechts (Position [math] 7 [/math]). Dann führt man den [math] U_E [/math] [math] = [/math] [math] U [/math] [math] R [/math] [math] U' [/math] [math] L' [/math] [math] U [/math] [math] R' [/math] [math] U' [/math] [math] L [/math] Algorithmus so oft aus, bis die Ecken an der richtigen Position sind. Die Eckenpermutation für die erste Ausführung ist [math] (586) [/math] und für die zweite [math] (568) [/math]. Die Kanten permutieren dabei nicht. Sollte keine Ecke an der richtigen Stelle sein, führt man den Algorithmus einfach einmal aus. Mit Hilfe von diesem werden die Ecken gegen den Uhrzeigersinn gedreht, wobei die vordere-rechte-obere Ecke (auch hier Position [math] 7 [/math]) bleibt. Dies funktioniert, da entweder [math] 0 [/math], [math] 1 [/math] oder [math] 4 [/math] Ecken an der richtigen Stelle sind.
Zur Korrektur der Orientierung betrachtet man eine verdrehte Ecke in Position [math] 7 [/math] und wiederholt den [math] O [/math] [math] = [/math] [math] R' [/math] [math] D' [/math] [math] R [/math] [math] D [/math] Algorithmus, - den man zur Eckenlösung bei der weißen Fläche schon verwendet hat - bis die gelbe Farbe nach oben zeigt. Damit die Kanten nicht permutieren, muss dabei die Anzahl der Ausführungen ein Vielfaches der [math] 3 [/math] sein. Danach dreht man die Ebene bis die nächste ungelöste Ecke in Position 7 ist und wiederholt dieses Verfahren, bis der Würfel gelöst ist. Da der Algorithmus derselbe ist, den man beim Eckenlösen der oberen Ebene benutzt hat, wird auch hier kein Eckcubie permutieren, sondern nur seine Orientierung ändern. [8]
Weitere Zauberwürfel
2x2 Zauberwürfel
Eigenschaften
- [math]4[/math] kleine cubies/Eckcubies
- [math]6[/math] verdrehbare Seiten, alle cubies verdrehbar
[math]\Rightarrow 3^·674^·160[/math] Möglichkeiten den Würfel zu verdrehen ([math]=\frac{8!\cdot 3^8}{3\cdot 6\cdot 4}[/math] Wobei die Berechnung im Nenner wie beim [math]3x3[/math]-Würfel für die möglichen Positionen der [math]8[/math] Ecken und deren Orientierungsmöglichkeiten steht -> siehe Ordnung (Formel in letzter Zeile des Abschnittes), und der Zähler für die Anzahl der Seiten, der Cubies einer Seite und deren Orientierungsmöglichkeit)
Lösungsstrategie
Betrachtung
Denkt man sich beim [math] 3x3 [/math] Cube die mittleren Cubies und somit auch deren anliegenden Kanten weg, somit bleiben nur noch die Eckcubies erhalten, welche den [math] 2x2 [/math] Cube darstellen.
Schlussfolgerung
Zum Lösen genügen die Schritte in der oberen und unteren Ebene des [math]3x3[/math] Cubes, welche die Ecken behandeln. Mit folgendem Unterschied in der unteren Ebene: Beim Tauschen der Ecken, können beim [math] 3x3 [/math] Würfel entweder [math]3[/math] oder [math]4[/math] Ecken vertauscht sein, wobei es beim [math]2x2[/math] Würfel nur [math]2[/math] vertauschte Ecken gibt. Für diesen Fall wird folgender neuer Algorithmus eingeführt:
- [math] L^2 [/math] [math] B^2 [/math] [math] L′ [/math] [math] F′ [/math] [math] L [/math] [math] B^2 [/math] [math] L′ [/math] [math] F [/math] [math] L′ [/math]
In Permutationsschreibweise gilt: Der Würfel wird erstmal um [math]C_U^2[/math], ([math]2[/math] Obere-Umdrehungen um die eigene Achse) gedreht, um so die zu lösende Fläche oben zu haben. Die Permutationsschreibweise wird von hinten nach vorne angewendet somit wird der Algorithmus von hinten nach vorne geschrieben und die einzelnen Drehungen in Permutations-Schreibweise übersetzt, dies sieht folgender Massen aus:
- [math] L′ [/math] [math] F [/math] [math] L′ [/math] [math] B^2 [/math] [math] L [/math] [math] F′ [/math] [math] L′ [/math] [math] B^2 [/math] [math] L^2 [/math]
- [math] (1 4 8 5) [/math] [math] (1 2 6 5) [/math] [math] (1 4 8 5) [/math] [math] (3 4 8 7) [/math] [math] (3 4 8 7) [/math] [math] (1 5 8 4) [/math] [math] (1 5 6 2) [/math] [math] (1 4 8 5) [/math] [math] (3 4 8 7) [/math] [math] (3 4 8 7) [/math] [math] (1 5 8 4) [/math] [math] (1 5 8 4) [/math]
Es gibt [math] 2 [/math] Fälle:
- Fall 1: Die [math] 2 [/math] ungelösten Cubies liegen diagonal an den Ecken [math] 6 [/math] & [math] 8 [/math] → Wende einmal Algorithmus an → nun folgt Fall [math] 2 [/math]
- Fall 2: Die [math] 2 [/math] ungelösten Cubies liegen nebeneinander an den Ecken [math] 6 [/math] & [math] 7 [/math] → Wende Algorithmus an, dann werden die Ecken [math] 6 [/math] & [math] 7 [/math] miteinander getauscht, in Permutationsschreibweise gilt hier: [math] (6 7) [/math]
Somit ist der 2x2 Würfel gelöst.
Megaminx
Eigenschaften
Der Megaminx[10] ist ein Dodekaeder und besteht so aus
- 12 Flächen (Daher 12 unbewegliche Mittelsteine)
- 20 Ecksteinen
- 30 Kantensteinen
Also vergleichsweise zur Ordnung des 3x3 [math](\rho, \sigma, x, y) \in S_{20} \times S_{30} \times (\mathbb{Z} / 3\mathbb{Z})^{20} \times (\mathbb{Z} / 2\mathbb{Z})^{30} [/math]
Daher gibt es nicht [math] 30!\cdot 2^{30}\cdot 20! \cdot 3^{20}[/math] mögliche Verdrehungen eines Megaminx, sondern [math]\frac{1}{12} \cdot 30!\cdot 2^{30}\cdot 20! \cdot 3^{20} \approx 10^{68}[/math].
Das sind 50 Magnituden mehr als beim 3x3. Eine schnelle Hypothese ist, dass der Megaminx viel schwerer zu lösen ist. Doch das ist nicht der Fall.
Beim Megaminx verschiebt man bei einem Zug nur 20% der Steine, also die Hälfte der Steine die man beim 3x3 verschiebt. Zudem hat man mehr Flächen zum Arbeiten - Sind die oberen zwei Reihen gelöst (Bild), hat man noch immer 6 freie Flächen die beliebig verdreht werden können.
Subjektiv jedoch ist der Megaminx schwerer zu lösen, denn es ist schwerer zwischen mehr Farben zu unterscheiden (Bild) und man sucht länger nach dem richtigen Stein (Bild).
Lösungsstrategie
Zünachst löst man intuitiv einen Stern, so ähnlich wie man beim 3x3 zuerst ein Kreuz löst. (Bild)
Danach die Ecken des Sterns, der Algorhitmus ist der selbe, jedoch bezeichnet hier [math]R[/math][math]U[/math]und [math]L[/math] andere Flächen. (Bild
Dann die zweite Reihe, wieder mit dem selben Algorhitmus und Flächen wie zuvor.
Danach löst man die darüber liegenden Kanten, dieser Schritt ist intuitiv lösbar. Da viele Fläschen noch nicht gelöst sind und man die daher frei bewegen kann.
Um die anliegenden Kanten zu lösen, positioniert man den passenden Stein über dem Mittelstein und führt den Algorhitmus [math]F'[/math] [math] R'[/math] [math] F'[/math] [math] F'[/math] [math] R[/math] [math] F[/math] bzw.[math] F[/math] [math] L[/math] [math] F[/math] [math] F [/math] [math]L' [/math] [math]F' [/math] aus.
Die nächsten Ecken und Kanten sind gleichzusetzen mit den ersten Ecken und Kanten des 3x3. Man hat noch eine komplette Fläsche zum lösen frei, genauso wie beim 3x3.
Nun formt man das letzte Kreuz. Zunächst die Orientierung der Kanten mit [math]F [/math] [math]U[/math] [math] R [/math] [math]U' [/math] [math]R' [/math] [math]F' [/math] entweder muss man diesen Algorhitmus ein mal (Drei Ecken ist richtig orientiert) oder zwei mal (Eine Ecken sind richtig orientiert) ausführen.
Um nun die Kanten an die Richtige position zu bringen führt man den Algorhitmus [math]R [/math] [math]U [/math] [math]U [/math] [math]R' [/math] [math]U' [/math] [math]R [/math] [math]U' [/math] [math]R' [/math] aus. Eventuell muss man diesen mehrfach ausführen.
Die Ecken an die richtige Position zu bringen ist wie beim 3x3 nur muss man hier 2 mal U ausführen. Also [math] R [/math] [math]U [/math] [math]U [/math] [math]R' [/math] [math]U' [/math] [math]U' [/math][math]L' [/math] [math]U[/math] [math] U [/math] [math]R [/math] [math]U' [/math] [math]U' [/math] [math]R' [/math] [math]L[/math]
Um die Ecken nun richtig zu orientieren führt man wie beim 3x3 den Algorhitmus [math]R' [/math] [math]D' [/math] [math]R [/math] [math]D [/math] aus bist die Ecke stimmt und dann dreht man die Nächste Ecke auf die Position der ersten und führt den Algorhitmus aus usw. bis alle Ecken gelößt sind.
Quellen
- ↑ https://de.wikipedia.org/wiki/Symmetrische_Gruppe
- ↑ https://mampf.mathi.uni-heidelberg.de/mediaforward/medium/16609/manuscript/ef7c2209ceb055a6c08e459784dca941.pdf
- ↑ https://mampf.mathi.uni-heidelberg.de/mediaforward/medium/16609/manuscript/ef7c2209ceb055a6c08e459784dca941.pdf.
- ↑ Christoph Bandelow: Inside rubik’s cube and beyond, Boston, 1982, ISBN 978-0-8176-3078-2
- ↑ Christoph Bandelow: Inside rubik’s cube and beyond, Boston, 1982, ISBN 978-0-8176-3078-2
- ↑ https://mampf.mathi.uni-heidelberg.de/mediaforward/medium/16609/manuscript/ef7c2209ceb055a6c08e459784dca941.pdf
- ↑ Christoph Bandelow: Inside rubik’s cube and beyond, Boston, 1982, ISBN 978-0-8176-3078-2
- ↑ https://cube3x3.com/wie-man-einen-zauberwurfel-rubiks-cube-lost-de/
- ↑ https://docplayer.org/82609247-Die-zauberwuerfel-werkstatt-baustein-rubiks-miniwuerfel-der-2x2x2.html
- ↑ https://de.wikipedia.org/wiki/Megaminx
Autoren
Gruppe "Gruppentheorie am Zauberwürfel": Jan Rüschkamp, Leonard Hörnis, Johanna Wolf, Verena Köder
Gruppe "Lösungsstrategien im Zusammenhang mit den Varianten vom klassischen Zauberwürfel": Anne Faber, Karl Frietsch Musulin, Lisa Bui