Konstruktion der Reellen Zahlen: Unterschied zwischen den Versionen
AlexFi (Diskussion | Beiträge) |
AlexFi (Diskussion | Beiträge) |
||
| (155 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
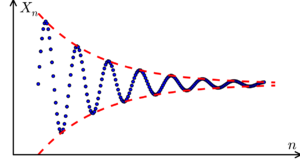
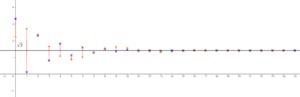
| − | = | + | Beim Konstruieren der <math> \mathbb{R}</math> tauchen schnell Probleme auf, da sie im Gegenteil zu den ganzen und rationalen Zahlen nicht Anhand einer Formel wie z.B. <math>\frac{p}{q}</math> mit <math> p \in \mathbb{Z}, q \in \mathbb{N}</math> aufgebaut werden können, darum versucht dieser Artikel, die reellen Zahlen mithilfe der Cauchy-Folge zu veranschaulichen.Wir nennen eine Folge <math>(x_n)_{n\in\mathbb{N}}</math> eine Cauchy-Folge, wenn es zu jedem Wert <math>\varepsilon>0 </math> eine Zahl <math>N \in \mathbb{N}</math> gibt mit der Eigenschaft, dass für alle Indizes <math>m,n > N</math> die Abschätzung <math>|x_m - x_n|\leq \varepsilon</math> gilt. Dies bedeutet, dass mit hinreichend großen Indizes die Differenz von Folgengliedern beliebig klein wird (siehe Bild). Dadurch lassen sich vor allem die reellen Zahlen <math> \mathbb{R}</math> konstruieren, wie hier gezeigt werden soll. Cauchy-Folgen sind benannt nach dem französischen Mathematiker Augustin Louis Cauchy (1789-1857) der den Weg zur modernen Analysis mit bereitet hat. Zudem wird hier behandelt, wo die reellen Zahlen auftauchen und wie sie konstruiert werden können. |
| + | [[Datei:Cauchy-Folge.png|rahmenlos|rechts|Für hinreichend große Indizes ist die Differenz beliebig klein]] | ||
| + | Bevor die Cauchy-Folge erklärt wird, betrachten wir aber das Heron-Verfahren, da wir hieran gut die Besonderheiten der reellen Zahlen sehen können. | ||
| + | |||
| + | =Augustin-Louis Cauchy= | ||
| + | Cauchy war ein sehr wichtiger Entwickler auf dem Gebiet der Analysis im frühen 19.Jahrhundert. In den 1820er-Jahren hat er das gesamte Gebiet der Reellen Analysis umgekehrt, indem er die Begriffe Grenzwert, Stetigkeit, Ableitung und Integral formuliert hat. Darüber hinaus hat er die Komplexe Analysis entwickelt. Deshalb sind heute viele Ergebnisse auf diesem Gebiet mit seinem Namen behaftet. Daneben führte Cauchy die erste sogenannte Revolution der Strenge in der Mathematik ein. | ||
| + | |||
| + | Augustin-Louis Cauchy wurde am 21.August 1789 geboren, also mitten in die französische Revolution hinein. Noch vor dieser war sein Vater ein hoher Beamter. Im Jahr 1794, als die Revolution bereits im Gang war, floh er mit seiner Familie in den kleinen Ort Arcueil und lebte dort abgeschieden. Ganz stark geprägt wurden die Kinder durch das Ausleben einer tiefen Religiosität, die sie auch später noch begleiten sollte. Die Ausbildung von Cauchy übernahm sein Vater, da er klassische Sprachen und Literatur selbst ausgezeichnet beherrschte. Schon hier zeigte sich aber beim Sohn ein ganz anderes besonderes Talent, nämlich das für Mathematik. | ||
| + | |||
| + | [[Datei:Augustin-Louis Cauchy 1901.jpg|max|rahmenlos|links]] | ||
| + | |||
| + | Zufällig hatte nun auch Joseph-Louis Lagrange ein Anwesen in Arcueil, sodass Cauchy sowohl ihm als auch anderen Wissenschaftlern, die bei Lagrange zu besuch waren, begegnen konnte.Lagrange war beeindruckt von den Fähigkeiten des jungen Mannes und deshalb auch interessiert an seiner Ausbildung. Zwei Jahre später kehrte die Familie nach Paris zurück, wo der Vater seine Karriere unter dem neuen Regime fortsetzen konnte und nun zum Generalsekretär des Senats - dessen Kanzler wiederum Laplace war - bestimmt wurde. Zuerst besuchte Cauchy eine humanistische Schule, bevor er 1805 an der Aufnahmeprüfung zur École Polytechnique teilnahm. Dort belegte er den zweiten Platz und nahm mit 16 Jahren das Studium an dieser Schule auf. Nach zwei Jahren Ausbildung mit Schwerpunkt auf Mathematik und Mechanik wechselte er zur École des Ponts et Chaussées für zwei Jahre und war 1810 mit nicht ganz 21 Jahren bereits Ingenieur. Dann ging er nach Cherbourg zum Aufbau des dortigen Hafens, der zu dieser Zeit eine große strategische Bedeutung für Militäroperationen gegen Großbritannien hatte. Hier entstanden erste mathematische Arbeiten zu sehr vielen Themen wie der Theorie der Brücken, den Polyedern oder den figurierten Zahlen. In Cherbourg blieb Cauchy fast drei Jahre, unter anderem weil seine Arbeit sehr gelobt wurde. Daneben beschäftigte er sich in seiner knappen Freizeit noch mit mathematischer Forschung. Im Selbststudium eignete er sich selbst Werke von Lagrange ([https://gallica.bnf.fr/ark:/12148/bpt6k86263h.image Traité des fonctions analytiques]) und Laplace ([[wikipedia:Traité_de_mécanique_céleste|Mécanique céleste]]) an. Seine mathematische Karriere begann 1811, als es ihm gelang ein Problem von Lagrange zu lösen. Um eine Krankheit auszukurieren, ging Cauchy 1812 für einige Zeit nach Paris zurück, wo er schließlich das Manuskript einer Arbeit über symmetrische Funktionen vervollständigte, die bereits jene grundlegenden Ideen enthielt, aus der später die Gruppentheorie hervorgehen sollte. In dieser Arbeit, die dann 1815 veröffentlicht wurde, benutzte er zum einen Methoden von Gauß, zum anderen aber auch neue Methoden um zahlentheoretische Resultate von Lagrange und Ruffini zu verallgemeinern. Zudem entwickelte er darin die Theorie der Determinanten. | ||
| + | |||
| + | Mittlerweile war Cauchys Interesse an der Ingenieurstätigkeit erloschen, und er wollte sich nun ganz der Mathematik widmen; deshalb versuchte er, eine Stelle in Paris zu bekommen, allerdings erfolglos. Unterdessen schrieb Cauchy eine Arbeit, in der er versuchte, die Anzahl der reellen Nullstellen einer algebraischen Gleichung vorherzubestimmen - ein Gebiet, mit dem er sich immer wieder beschäftigen sollte. Hohe Reputation erlangte er dann mit einer Abhandlung zur Berechnung bestimmter Integrale. Hier zeigte sich bereits die mathematische Vielseitigkeit von Cauchy, die er im Laufe seines Lebens entwickelte. Im Laufe seines Lebens veröffentlichte er sieben Bücher und mehr als 800 wissenschaftliche Arbeiten. | ||
| + | |||
| + | Nachdem mehrere Versuche, in die Akademie der Wissenschaften gewählt zu werden, erfolglos geblieben waren, wurde Cauchy, der Royalist war, nach der Machtübernahme der Bourbonen im Jahr 1816 letztlich zum Mitglied der Akademie bestimmt, statt gewählt. Dieser Erfolg kostete ihn jedoch die Freundschaft einiger Leute, da im Gegenzug zum Beispiel Monge und Carnot aus der Akademie ausgeschlossen wurden. Kurze Zeit später wurde Cauchy zum Professor an der École Polytechnique für Analysis und Mechanik ernannt. Bei den Studenten war Cauchy beliebt, er galt als unermüdlich, gutmütig und geduldig erklärend. Allerding beschwerten sich einige Studenten über seine Zeit-Überziehung sowie über seine royalistischen Ansichten. | ||
| + | |||
| + | In seinen Vorlesungen entwickelte er ferner einen neuen Strengebegriff in der Analysis. Zu dieser Zeit war der Begriff der Funktion nämlich noch schwammig, denn es wurde mit unendlichen Summen gerechnet, ohne sich die Frage nach deren Konvergenz zu stellen, was dann einige Paradoxien hervorrief. Außerdem waren die grundlegenden Begriffe des Integrals und der Ableitung noch nicht genau definiert worden. In seinem aus Vorlesungen hervorgehenden Werk ''Analyse algébrique'' befasste sich Cauchy mit all diesen grundlegenden Problemen der Analysis. Er lieferte eine exakte Definition des unendlich Kleinen, wozu er den Begriff des Grenzwertes mit etwa den Orten einführte, wie sie auch heute noch verwendet werden. Damit konnte er dann relativ leicht Folgen definieren und davon ausgehend zur genauen Definition von Ableitung und Integral weiter schreiten. Ähnliche Fortschritte hatte zeitgleich der böhmische Mathematiker Bolzano in Prag erzielt. | ||
| + | |||
| + | Weiterhin kann man sagen, dass Cauchy den Begriff der Konvergenz von unendlichen Summen einführte und zudem Kriterien fand, mit deren Hilfe man über die Konvergenz von unendlichen Summen Aussagen treffen kann. Dabei entwickelte Cauchy die Infinitesimalrechnung aus dem Mittelwertsatz, der seit Lagrange bekannt war. Zu der von Cauchy eingeführten mathematischen Strenge erzählt die Überlieferung, dass Laplace, als Cauchy sein Werk während eines wissenschaftlichen Treffens präsentierte, schleunigst nach Hause eilte und sich dort so lange einschloss, bis er alle seine unendlichen Summen, die er in seiner ''Himmelsmechanik'' verwendet hatte, überprüft hatte. Glücklicherweise hielten tatsächlich alle seiner unendlichen Summen dem ''[https://de.wikipedia.org/wiki/Cauchy-Kriterium Cauchyschen Konvergenztest]'' stand. | ||
| + | |||
| + | In seinen wissenschaftlichen Forschungsarbeiten war Cauchy weniger streng. Zum Beispiel hielt er es nie für nötig, für seine von ihm verwendeten Funktionen Stetigkeit nachzurechnen, immerhin ein Begriff, den er selbst streng definiert hatte. | ||
| + | |||
| + | Interessanterweise hatte Cauchy sogar Pläne, die Lehrinhalte an der École Polytechnique zu reformieren. Mit seinem ''[[wikipedia:Cours_d'Analyse|Cours d´Analyse]]'' strebte er die selbe Strenge an, die die Geometrie zu dieser Zeit schon hatte. Diese scheiterten jedoch zum großen Teil. Denn es gab Einwände, sie seien zu sehr theoretisch orientiert und überambitioniert. Schließlich wolle man ja Ingenieure ausbilden und keine Mathematiker. | ||
| + | |||
| + | [[Datei:99903BB.jpg|mini|rechts|Buch von Lagrange über die Theorie der analytischen Funktionen, die sich Cauchy im Selbststudium aneignete]] | ||
| + | |||
| + | Diese Zeit, also während der Restauration, war die fruchtbarste Schaffensperiode für Cauchy. Nun fixierte er sich auf vier Themenbereiche. Der erste war die Lehrtätigkeit, mit Schwerpunkt auf theoretischer Mechanik und Analysis. Daraus gingen die bereits beschriebenen fundamentalen Definitionen hervor. Der zweite war die mathematische Physik. Daraus resultierten wiederum zwei große Arbeiten über die Theorie der Wellenausbreitung und über die Elastizitätstheorie. Und drittens entwickelte Cauchy nahezu im Alleingang das bahnbrechende neue Gebiet der komplexen Analysis, das erst langsam an Anerkennung gewann, später aber gewaltige Auswirkungen haben sollte. Außerdem schuf er eine detaillierte Ausarbeitung der Theorie der Differentialgleichungen. Dabei erkannte er die Notwendigkeit, Existenzbeweise von Lösungen führen zu müssen. 1816 erhielt er einen Preis der Pariser Akademie für seine Lösung eines Problems der Hydromechanik. | ||
| + | |||
| + | All das schaffte Cauchy, bevor er 28 Jahre alt war. Aufgrund seiner hohen Produktivität würde auch eine ausführliche Aufzählung der Errungenschaften Cauchys jeden Rahmen sprengen. Hier nur einige Sätze und Begriffe aus der Mathematik, die seinen Namen tragen: Cauchysche Abschätzungsformel, Cauchysche Anfangswertprobleme, Cauchysche Integralformel, Cauchyscher Integralsatz, Existenzsatz von Cauchy, Cauchy-Riemannsche partielle Differentialgleichungen, Cauchy-Bunjakowsji-Schwarzsche-Ungleichung, Cauchysches Quotientenkriterium, Cauchy-Reihenproduktsatz, Cauchysches Wurzelkriterium und Cauchy-Folge, um die es hier besonders gehen soll. | ||
| + | |||
| + | 1818 heiratete Cauchy und pflegte nun auch in seiner eigenen Familie die religiöse Tradition, die ihm zu Hause mitgegeben worden waren. Lange Zeit später, von 1830 an, änderte sich sein Leben von Grund auf. Nach der Revolution von 1830 ging Cauchy freiwillig ins Exil. Damit gab er seiner Verbundenheit mit dem gestürzten Bourbonenkönig Karl X. Ausdruck. Zuerst siedelte Cauchy in die Schweiz über, arbeitete dann von 1831 bis 1833 in Turin. Danach wurde er von Karl X. für fünf Jahre als Erzieher in den Bourbonen Exil-Ort Prag geholt. Cauchy hielt allerdings während dieser Zeit immer Kontakt zu den französischen Wissenschaftsinstitutionen. Schließlich wurde im Jahr 1835 in Paris die Zeitschrift Comptes Rendues der Akademie der Wissenschaften ins leben gerufen, die Cauchy mit vielen ausgedehnten Arbeiten geradezu überflutete. Seinetwegen wurde später sogar ein Seitenlimit von vier Seiten pro Arbeit eingeführt. Manchmal reichte Cauchy auch unvollständige Arbeiten ein, oder gar mehrere unfertige Skizzen zu einer Problematik, teilweise sogar ohne zu einem Ergebnis zu gelangen. Wegen seiner hohen Zahl an Publikationen schließlich würdigte man seine Arbeit in Paris sehr. Aufgrund seiner Selbstbezogenheit aber, seiner Unduldsamkeit gegenüber jüngeren Kollegen und nicht zuletzt aufgrund seiner religiösen und politischen Ansichten war Cauchy als Person nicht nur beliebt. Trotz allem war er in seinen Gutachten der Arbeiten anderer äußerst fair, würdigte deren Verdienste und gab auch eigene Fehler zu. | ||
| + | |||
| + | Schließlich kehrte er 1838 nach Paris zurück. Da Cauchy es ablehnte, einen Treueid auf die Regierung abzuleisten, konnte er zunächst keine Anstellung bekommen. Dann wurde er 1839 in das Bureau des Longitudines, das Amt für Maße und Gewichte, gewählt. Dort wurde er zwar von der Regierung nicht offiziell bestätigt, aber auch nicht wieder entfernt. Mit der Revolution von 1848 wurde der Treueid dann abgeschafft, so dass paradoxerweise gerade die liberalen Kräfte dem Royalisten Cauchy wieder eine legale Anstellung ermöglichten. | ||
| + | |||
| + | Cauchy griff zwar nie in die Politik ein, jedoch benutzte ihn die Kirche oft als Aushängeschild für ihre Ziele. So sollte er ein Beispiel für die Verknüpfung von Glaube und Wissenschaft sein, also eine auf der Vernunft basierende Bestätigung der Richtigkeit der kirchlichen Politik. Während eines Besuchs in Paris sagte Abel in diesem Zusammenhang über Cauchy: "Cauchy ist extrem katholisch und bigott. Das ist eine sehr seltsame Sache bei einem Mathematiker." | ||
| + | |||
| + | 1857 erkrankte Cauchy, woraufhin ihm der Pariser Kardinal die Letzte Ölung erteilte. Am 23.Mai 1857 starb er. | ||
| + | |||
| + | =Heron-Verfahren= | ||
| + | Das Heron-Verfahren war schon den Babyloniern von vor 4000 Jahren bekannt, daher wird es auch als Babylonisches Wurzelziehen bezeichnet. Dabei wird die Wurzel von x anhand der Formel <math>a_{n+1}:=\frac{1}{2}(a_n+\frac{x}{a_n})</math> approximiert. Dabei ist es egal, welcher Startwert <math> a_0 </math> gewählt wird. Ein Beispiel zeigt: | ||
| + | |||
| + | [[Datei:Heron.jpg|max|right|Geometrische Interpretation des Heron-Verfahrens]] | ||
| + | Wurzel von 2: | ||
| + | |||
| + | <math> a_0 = 1 </math> | ||
| + | |||
| + | <math> a_1 = </math> 1/2(1 + 2/1) = 1,5 | ||
| + | |||
| + | <math> a_2 = </math> 1/2(1,5 + 2/1,5) = 1,4166666... | ||
| + | |||
| + | <math> a_3 = </math> 1/2(1,41666667 + 2/1,41666667) = 1,41421143847... | ||
| + | |||
| + | ... | ||
| + | |||
| + | <math> a_8 = </math> 1,4142135624... | ||
| + | |||
| + | Zum Vergleich mit dem Startwert <math> a_0=3 </math> | ||
| + | |||
| + | <math> a_0 = 3 </math> | ||
| + | |||
| + | <math> a_1 = </math> 1/2(3 + 2/3) = 1,833333... | ||
| + | |||
| + | <math> a_2 = </math> 1/2(1,833333 + 2/1,833333) = 1,4621212105 | ||
| + | |||
| + | ... | ||
| + | |||
| + | <math> a_8 = </math> 1,4142135624... | ||
| + | |||
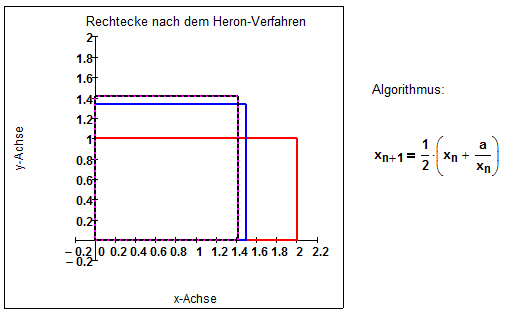
| + | Eine geometrische Interpretation des Heron-Verfahrens ist die folgende: Gesucht ist die Seitenlänge eines Quadrats mit Flächeninhalt <math> x </math>. Dazu wird zunächst ein Rechteck konstruiert, von dem bekannt ist, dass die Fläche <math> x </math> beträgt (z.B. mit einer Seite der Länge <math> x_0=x </math> und einer Seite der Länge <math> y_0=1 </math>). Nun wird schrittweise mittels des Algorithmus des Heron-Verfahrens der Wert <math> x_i </math> angepasst und <math> y_i=\frac{x}{x_i} </math> gesetzt. Dieses Verfahren wird bis zur gewünschten Genauigkeit fortgeführt. | ||
=Zahlen= | =Zahlen= | ||
| + | ===Wichtige Sätze der Analysis beruhen auf der Vollständigkeit von <math> \mathbb{R} </math> === | ||
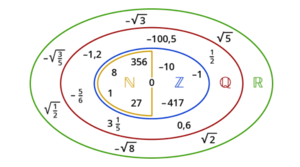
| + | Bei der Einführung der Zahlensysteme kann man so vorgehen, dass man mit den natürlichen Zahlen <math>\mathbb{N}</math> beginnt. Als Differenzen von natürlichen Zahlen erhält man die ganzen Zahlen <math>\mathbb{Z}</math>, als Quotienten von ganzen Zahlen die rationalen Zahlen <math>\mathbb{Q}</math>. In <math>\mathbb{Q}</math> kann man jetzt schon recht gut Analysis betreiben, etwa den Konvergenzbegriff einführen. Die Folge <math>(\frac{1}{n})_{n\in\mathbb{N}}</math> ist zum Beispiel aus <math>\mathbb{Q}</math> und konvergiert gegen die Null. | ||
| − | =Cauchy= | + | Es gibt aber auch andere Folgen in <math>\mathbb{Q}</math>, die sich wie konvergente Folgen verhalten, deren Grenzwert aber nicht in <math>\mathbb{Q}</math> liegt. Ein Beispiel dafür ist die Folge, die beim Heron-Verfahren zur Approximation von <math>\sqrt{2}</math> konstruiert wird. Beschränkt man sich nur auf <math>\mathbb{Q}</math>, so ist eine solche Folge nicht konvergent, denn sie besitzt keinen Grenzwert in <math>\mathbb{Q}</math>, ist aber dennoch eine Cauchyfolge. |
| + | |||
| + | [[Datei:Zahlbereich.png|rahmenlos|rechts|Zahlen und ihre Zahlbereiche]] | ||
| + | |||
| + | '''Beispiel:''' Wir berechnen die Cauchy-Folgeneigenschaft der Folge aus dem Heron-Verfahren nach. Die Folge ist definiert durch <math>a_0=2, a_n=1/2(a_{n-1} + 2/(a_{n-1})), n\in \mathbb{N}</math>. | ||
| + | |||
| + | Mittels vollständiger Induktion zeigt man, dass <math> a_n \in [1,2] \text{ für alle } n\in \mathbb{N}_0</math> gilt. Weiterhin folgt | ||
| + | |||
| + | <math>a_{n+1} - a_n = 1/2 ( a_n + 2/a_n - a_{n-1} -2/a_{n-1}) = (1/2 - 1/(a_n * a_{n-1}))(a_n - a_{n-1})</math> für <math> n \in \mathbb{N}</math>. Somit ergibt sich: | ||
| + | |||
| + | <math> |a_{n+1} - a_n|\leq 1/2 |a_n - a_{n-1}| \leq (1/2)^n |a_1 - a_0| </math> | ||
| + | |||
| + | Für <math>m>n</math> folgt mit der geometrischen Reihe: | ||
| + | <math> |a_m - a_n|\leq \sum\nolimits_{k=n}^{m-1} |a_{k+1} - a_k|\leq \sum\nolimits_{k=n}^{m-1} (1/2)^k|a_1 - a_0| = (1/2)^n|a_1 - a_0| \sum\nolimits_{k=0}^{m-n-1} (1/2)^k \leq (1/2)^{n-1}|a_1 - a_0|</math> | ||
| + | |||
| + | Indem wir n groß genug wählen, wird die Schranke auf der rechten Seite kleiner als jedes vorgegebene <math>\varepsilon>0</math>. Wir haben damit den Nachweis erbracht, dass <math>(x_n)_{n\in\mathbb{N}} </math> eine Cauchy-Folge ist. | ||
| + | |||
| + | ===Wichtige vorbereitende Definitionen und Sätze=== | ||
| + | |||
| + | '''Definition 1:''' Eine Folge <math>(a_n)_{n\in\mathbb{N}}</math> heißt Nullfolge, wenn <math>\lim_{n\to\infty} a_n = 0</math> gilt. | ||
| + | |||
| + | '''Definition 2:''' Eine Folge <math>(a_n)_{n\in\mathbb{N}}</math> heißt Fundamentalfolge oder Cauchy-Folge, wenn gilt: <math> \forall \varepsilon>0 , \exists n_1 \in \mathbb{N} : d(a_n,a_m)<ε , \forall n,m\geq n_1</math>. | ||
| + | |||
| + | '''Definition 3:''' Die Anordnungsaxiome: Ein angeordneter Körper ist ein Körper K zusammen mit einer Teilmenge <math>P \subset K</math>. Diese erfüllt folgende Ordnungsrelationen oder Anordnungs[[Eine mathematische Aussage, die nicht beweisbar ist|axiome]]: | ||
| + | |||
| + | '''O1''' Für jedes <math>a \in K </math>gilt genau eine der folgenden Aussagen: | ||
| + | {| | ||
| + | |- | ||
| + | | i) || <math>a\in P</math> || a>0 | ||
| + | |- | ||
| + | | ii) || a = 0 || a = 0 | ||
| + | |- | ||
| + | | iii) || <math>-a\in P</math> || -a>0 | ||
| + | |} | ||
| + | |||
| + | '''O2''' | ||
| + | {| | ||
| + | |- | ||
| + | | <math>a,b\in P \Rightarrow a+b, ab \in P</math> | ||
| + | |- | ||
| + | | <math>a,b >0 \Rightarrow a+b>0 \land ab>0 </math> | ||
| + | |} | ||
| + | |||
| + | '''Definition 4:''' Es sei M eine Teilmenge des angeordneten Körpers K. Ein Element <math>s\in K</math> heißt Supremum vom M, falls gilt: | ||
| + | * s ist eine obere Schranke von M | ||
| + | * Ist t eine obere Schranke von M, so folgt: <math> t \geq s </math> | ||
| + | D.h. s ist die "kleinste obere Schranke" von M. | ||
| + | |||
| + | Eine Folge reeller Zahlen ist eine Abbildung <math> f:\mathbb{N} \to \mathbb{R} </math>. Wir schreiben <math> f=(a_n)_n \in \mathbb{N} </math>. | ||
| + | |||
| + | '''Definition 5:''' Wir sagen, dass eine Folge <math> f:\mathbb{N} \to K </math>konvergiert, wenn ein <math> a\in K </math> existiert, sodass für alle <math>\varepsilon > 0 </math> ein <math> N_0\in\mathbb{N} </math> existiert, sodass <math> |a_n-a| < \varepsilon </math> für alle <math> n\geq N_0 </math>. Wir nennen <math> a </math> dann den Limes der Folge und schreiben <math> a=lim_{n\to \infty} a_n </math>. | ||
| + | |||
| + | [[Datei:DTV-Bild-Selbstgemacht.png|mini|ungerahmt|rechts|Ähnlich wie beim Heron-Verfahren, sieht man hier, wie sich die Werte von a<sub>x</sub> an a nähern und irgendwann in der ε-Umgebung liegen]] | ||
| + | |||
| + | '''Satz:''' Jede konvergente Folge ist eine Cauchy-Folge. | ||
| + | |||
| + | '''Beweis:''' Ist <math>\varepsilon > 0 </math> vorgegeben, so ist auch <math>\frac{\varepsilon}{2} > 0 </math> und es gibt wegen der Konvergenz ein <math> N_0</math>, sodass <math>|a-a_n| < \frac{\varepsilon}{2}, \forall n \geq N_0</math>. Dann gilt wegen der Dreiecksungleichung <math>|a_n-a_m|=|(a_n - a)+(a-a_m)|\leq |a-a_n|+|a-a_m|< \frac{\varepsilon}{2} + \frac{\varepsilon}{2} = \varepsilon , \forall n,m\geq N_0</math>. | ||
| + | Die Umkehrung gilt nicht in <math>\mathbb{Q}</math>! (Aber in <math>\mathbb{R} \lor \mathbb{C}</math>) | ||
| + | |||
| + | Wir wollen nun <math>\mathbb{Q}</math> so erweitern/ vervollständigen, dass in der vervollständigten Menge jede Cauchy-Folge konvergiert. Einen Raum mit dieser Eigenschaft nennt man vollständig. Die Vervollständigung von <math>\mathbb{Q}</math> heißt vollständige Hülle von <math>\mathbb{Q}</math>. | ||
| + | |||
| + | ===Konstruktion der vollständigen Hülle von <math>\mathbb{Q}</math>=== | ||
| + | Man könnte zunächst daran denken, die Cauchy-Folgen selbst als Elemente der zu konstruierenden Menge zu verwenden. Doch zeigt schon die Betrachtung konvergenter Cauchy-Folgen, dass es jeweils beliebig viele Folgen mit gleichem Grenzwert (Limes) gibt. Sind <math>(a_n)_{n\in\mathbb{N}} </math> und <math>(b_n)_{n\in\mathbb{N}} </math> zwei solcher Folgen, so ist allerdings <math>(a_n-b_n)_{n\in\mathbb{N}} </math> eine Nullfolge. Dies führt zu einer Klasseneinteilung in der Menge aller Cauchy-Folgen durch die Einführung einer Äquivalenzrelation: Zwei Folgen werden genau dann miteinander identifiziert, wenn ihre Differenz eine Nullfolge ist. Man prüft leicht nach, dass dies in der Tat eine Äquivalenzrelation ist. Wir bezeichnen nun den Abschluss von <math>\mathbb{Q}</math> nun als <math>\mathbb{\bar Q}</math>. Damit kann man <math>\mathbb{\bar Q}</math> anordnen und einen Absolutbetrag einführen, durch den in <math>\mathbb{\bar Q}</math> eine Metrik und damit eine topologische Struktur eingeführt werden kann, durch die <math>\mathbb{\bar Q}</math> die Eigenschaften einer topologischen Gruppe erhält. Es zeigt sich, dass jede Cauchy-Folge in <math>\mathbb{\bar Q}</math> konvergiert. <math>\mathbb{\bar Q}</math> ist die gesuchte vollständige Hülle von <math>\mathbb{Q}</math>. | ||
| + | |||
| + | ===Einbettung von <math>\mathbb{Q}</math> in <math>\mathbb{\bar Q}</math>=== | ||
| + | Die Abbildung <math> \iota: \mathbb{Q}\to \mathbb{\bar Q} </math> definiert durch <math> \iota(p)=[(p,p,p,\dots)]</math> ist eine injektive strukturverträgliche Abbildung. Strukturverträglichkeit bedeutet hier Verträglich mit der Gruppenstruktur von (<math>\mathbb{Q}</math>,+) und der topologischen Struktur. | ||
| + | |||
| + | Aus der Konstruktion von <math>\mathbb{\bar Q}</math> ergibt sich auch die universelle Eigenschaft von <math> \iota </math>. Denn ist M irgendeine Menge mit den geforderten Strukturmerkmalen (d.h. Jede Cauchy-Folge ist konvergent), und lässt sich <math>\mathbb{Q}</math> in M einbetten durch die strukturverträgliche Abbildung <math>f:\mathbb{Q} \to M</math>, so kann zunächst gefolgert werden, dass <math>(f(a_n))</math> eine Cauchy-Folge in M ist, wenn <math>(a_n)</math> eine Cauchy-Folge in <math>\mathbb{Q}</math> ist. <math>(f(a_n))</math> konvergiert wegen der Struktureigenschaften von M dann gegen ein Element <math>r' \in M</math>. Die Abbildung <math>g:\mathbb{\bar Q} \to M</math> definiert durch <math>g([a_n])= r'</math> bettet dann <math>\mathbb{\bar Q}</math> in M ein, und es ist <math>f = g \circ i</math>. <math>\mathbb{\bar Q}</math> ist damit die kleinste <math>\mathbb{Q}</math> umfassende Menge, in der jede Cauchy-Folge konvergiert, und ist bis auf Isomorphie eindeutig bestimmt. | ||
| + | |||
| + | ===Isomorphie von <math>\mathbb{\bar Q}</math> und <math>\mathbb{R}</math>=== | ||
| + | Die [https://de.wikipedia.org/wiki/Isomorphismus Isomorphie] von <math>\mathbb{\bar Q}</math> und <math>\mathbb{R}</math> ist selbsterklärend da <math>\mathbb{\bar Q}</math> und <math>\mathbb{R}</math> gleich definiert sind. Dies folgt also daraus, dass gezeigt wurde, dass <math>\mathbb{\bar Q}</math> die kleinste <math>\mathbb{Q}</math> umfassende Menge ist, die die Bedingungen der Cauchy-Folge erfüllt. Denn aus dem [https://de.wikipedia.org/wiki/Rationale_Zahl Stetigkeitsbegriff<sup>(3.Eigenschaften)</sup>] wissen wir, dass der Grenzwert einer gegen <math>\sqrt{2}</math> konvergierenden Folge in <math>\mathbb{Q}</math> nicht existiert, aber dafür in <math>\mathbb{\bar Q}</math>, da dies die kleinste Hülle ist, die <math>\mathbb{Q}</math> umschließt und somit den [https://de.wikipedia.org/wiki/Dichte_Teilmenge Dichtheitsbegriff <sup>(2.Beispiele)</sup>] erweitern und stetige Funktionen auf <math>\mathbb{\bar Q}</math> zulassen. | ||
| + | Die topologische Struktur von <math>\mathbb{\bar Q}</math> heißt reelle Topologie im Unterschied zur sogenannten rationalen Topologie von <math>\mathbb{Q}</math>. Durch <math>[(a_n)]*[(b_n)]:=[(a_n * b_n)]</math> und <math>[(a_n)]^{-1} :=[a_n^{-1}]</math> für <math>a_n \neq 0</math> lässt sich die algebraische Struktur von <math>\mathbb{\bar Q}</math> zu einer Körperstruktur derart erweitert, dass <math>\mathbb{R}</math> und <math>\mathbb{\bar Q}</math> bijektiv unter Erhaltung aller Strukturmerkmale aufeinander abgebildet werden können.<sup>[1]</sup> | ||
| + | |||
| + | Wir bezeichnen fortan <math>\mathbb{\bar Q}</math> als <math>\mathbb{R}</math>. | ||
=Cauchy-Folge= | =Cauchy-Folge= | ||
| + | Sei C die Menge der Cauchy-Folgen auf <math>\mathbb{Q}</math>. | ||
| + | |||
| + | ===Eigenschaften von Cauchy-Folgen=== | ||
| + | Seien <math> (x_n)_{n\in\mathbb{N}},(y_n)_{n\in\mathbb{N}} \subset C </math>. Dann gilt: | ||
| + | |||
| + | a) <math> (x_n)_{n\in\mathbb{N}} </math> ist beschränkt. | ||
| + | |||
| + | b) <math> (x_n + y_n)_{n\in\mathbb{N}} \subset C</math> | ||
| + | |||
| + | c) <math> (x_n * y_n)_{n\in\mathbb{N}} \subset C</math> | ||
| + | |||
| + | d) Ist <math>(x_n)_{n\in\mathbb{N}} </math> keine Nullfolge <math>\Rightarrow \exists ε>0, ε\in\mathbb{Q}, N\in\mathbb{N}</math>, sodass entweder <math>x_n\geq ε, \forall n \geq N</math> oder <math>x_n\leq -ε, \forall n \geq N</math>, die die Axiome O1 und O2 erfüllen. Statt <math>a \in P</math> schreiben wir a>0, sprich: "a positiv". | ||
| + | |||
| + | e) Ist <math> (x_n)_n\in\mathbb{N} </math> keine Nullfolge, <math>x_n\neq 0, \forall n\in \mathbb{N} \Rightarrow (x_n^{-1})\in C </math> | ||
| + | |||
| + | Man kann die Cauchyfolgen-Eigenschaft (siehe Definition) in vollständigen metrischen Räumen verwenden ohne Kenntnis über den Grenzwert zu haben. | ||
| + | Folgende Konvergenzkriterien gibt es (werden aber nicht unbedingt erklärt, da sie nicht von besonderer Wichtigkeit hier sind): Majorantenkriterium, Einschließungskriterium, Monotoniekriterium, Bolzano-Weierstraß, Cauchy-Kriterium (Eine reelle Zahlenfolge konvergiert genau dann gegen eine reelle Zahl, wenn sie eine Cauchy-Folge ist. Es gilt: <math>(a_n)_{n\in\mathbb{N}}</math> ist Cauchy-Folge <math>\Leftrightarrow (a_n)_{n\in\mathbb{N}}</math> ist konvergent. Dieses Kriterium gilt wie oben erwähnt zum Beispiel in <math>\mathbb{R}</math>, aber nicht in <math>\mathbb{Q}</math>.) | ||
| + | |||
| + | Jede Cauchy-Folge in <math>\mathbb{R}</math> ist konvergent. Dieser Satz lässt sich mit dem [https://de.wikipedia.org/wiki/Satz_von_Bolzano-Weierstra%C3%9F Satz von Bolzano Weierstraß] zeigen. Diese Implikation gilt nicht in <math> \mathbb{Q} </math> (wie oben bereits am Beispiel der Folge mit Grenzwert <math> \sqrt{2} </math> gezeigt). Dies ist ein substantieller Unterschied zwischen den rationalen und den reellen Zahlen: Die reellen Zahlen sind vollständig, die rationalen hingegen nicht. (Wir nennen einen normierten Raum vollständig, wenn jede Cauchy-Folge konvergiert.) | ||
| + | |||
| + | Die Vollständigkeit der Reellen Zahlen muss man bei der Definition dieser durch ein Axiom, also eine nicht beweisbare Voraussetzung, verankern. Dazu gibt es verschiedene Vollständigkeitsaxiome, die verwendet werden können: Dedekindsche Schnitte, Intervallschachtelung, Cauchy-Kriterium, Satz von Bolzano-Weierstraß,... | ||
| + | |||
| + | = Konstruktion über Cauchy = | ||
| + | |||
| + | ===Konstruktion der Menge <math>\mathbb{R}</math> als Körper=== | ||
| + | [[Datei:DMV-Cauchy.png|mini|rechts|Zwei äquivalente Cauchy-Folgen: die Folge der Abstände, dargestellt durch die gestrichelten Linien, ist eine Nullfolge.]] | ||
| + | Zwei Cauchy-Folgen <math> (x_n)_n\in\mathbb{N},(y_n)_n\in\mathbb{N} </math> heißen äquivalent <math> (x\sim y)</math>, falls <math> x_n - y_n \to 0</math>. | ||
| + | |||
| + | Wir definieren nun <math>\mathbb{R}</math> als die Menge dieser Äquivalenzklassen. | ||
| + | |||
| + | '''Eigenschaften:''' | ||
| + | |||
| + | a) (<math>\mathbb{R}</math>, +) ist eine abelsche Gruppe | ||
| + | |||
| + | b) ( <math>\mathbb{R}</math>\{0}, * ) ist eine abelsche Gruppe | ||
| + | |||
| + | c) Es gilt das Distributivgesetz | ||
| + | |||
| + | d) (<math>\mathbb{R}</math>, +, *) ist ein Körper | ||
=Quellen= | =Quellen= | ||
* Mathematik, Springer-Spektrum, ISBN: 978-3-662-56740-1, S.190, 1053, 1173 | * Mathematik, Springer-Spektrum, ISBN: 978-3-662-56740-1, S.190, 1053, 1173 | ||
| − | * Höhere Mathematik, Verlag Harri Deutsch, ISBN: 978-3-8171-1872-4, | + | * Höhere Mathematik, Verlag Harri Deutsch, ISBN: 978-3-8171-1872-4, S.345, 351, 388 |
* Grundwissen Mathematikstudium, Springer-Spektrum, ISBN: 978-3-8274-2308-5, S.297, 772 | * Grundwissen Mathematikstudium, Springer-Spektrum, ISBN: 978-3-8274-2308-5, S.297, 772 | ||
| − | * Lexikon der Mathematik BAND:1, Spektrum Akademischer Verlag, ISBN: 3- | + | * Lexikon der Mathematik BAND:1, Spektrum Akademischer Verlag, ISBN: 978-3-662-53498-4, S.292ff. |
| − | |||
* Springer-Taschenbuch der Mathematik, Springer-Spektrum, ISBN: 978-3-8351-0123-4, S.243 | * Springer-Taschenbuch der Mathematik, Springer-Spektrum, ISBN: 978-3-8351-0123-4, S.243 | ||
| − | * dtv-Atlas der Mathematik Band 1, Dtv, ISBN: 3-423-03007- | + | * dtv-Atlas der Mathematik Band 1, Dtv, ISBN: 978-3-423-03007-6, S.61 |
| − | * Rechnen und | + | * Rechnen und Mathematik, Bertelsmann Lexikon-Verlag, Buch-Nr. 1599'1180, S.447 |
| + | * Die bedeutendsten Mathematiker, matrixwissen, ISBN: 978-3-86539-916-8, S.107ff. | ||
| + | * https://www.mathematik.de/algebra/179-erste-hilfe/zahlenbereiche/reelle-zahlen/2441-cauchy-folgen | ||
| + | |||
| + | =Bildnachweis= | ||
| + | * http://mathphys-online.de/heronverfahren-numerische-berechnung-von-quadratwurzeln/#prettyPhoto | ||
| + | * https://www.kapiert.de/reelle-zahlen-zahlenbereiche-untersuchen | ||
| + | * https://en.wikipedia.org/wiki/Augustin-Louis_Cauchy | ||
| + | * https://www.haufe-lutz.de/detail/99903BB/ (Stand 18.09.21/da Onlineshop) | ||
| + | * https://www.mathematik.de/algebra/179-erste-hilfe/zahlenbereiche/reelle-zahlen/2441-cauchy-folgen | ||
| + | |||
| + | =Weiterführende Literatur= | ||
| + | * Abhandlung über bestimmte Integrale zwischen imaginären Grenzwerten (Oswalds Klassiker 112 (1900)) | ||
| + | * <sup>[https://link.springer.com/content/pdf/10.1007%2F978-3-662-59230-4.pdf]</sup> Mit Mathe richtig anfangen, Springer Spektrum, ISBN: 978-3-662-59230-4, S.225/Kapitel 5 | ||
| + | * https://www.mathematik.de/algebra/179-erste-hilfe/zahlenbereiche/reelle-zahlen/2441-cauchy-folgen | ||
| + | * https://www.mathematik.de/ | ||
=Autoren= | =Autoren= | ||
| − | + | * | |
| − | + | * Alexander Fichtelmann | |
| + | * Immanuel Klevesath | ||
| + | * | ||
Aktuelle Version vom 14. Oktober 2021, 13:44 Uhr
Beim Konstruieren der [math] \mathbb{R}[/math] tauchen schnell Probleme auf, da sie im Gegenteil zu den ganzen und rationalen Zahlen nicht Anhand einer Formel wie z.B. [math]\frac{p}{q}[/math] mit [math] p \in \mathbb{Z}, q \in \mathbb{N}[/math] aufgebaut werden können, darum versucht dieser Artikel, die reellen Zahlen mithilfe der Cauchy-Folge zu veranschaulichen.Wir nennen eine Folge [math](x_n)_{n\in\mathbb{N}}[/math] eine Cauchy-Folge, wenn es zu jedem Wert [math]\varepsilon\gt 0 [/math] eine Zahl [math]N \in \mathbb{N}[/math] gibt mit der Eigenschaft, dass für alle Indizes [math]m,n \gt N[/math] die Abschätzung [math]|x_m - x_n|\leq \varepsilon[/math] gilt. Dies bedeutet, dass mit hinreichend großen Indizes die Differenz von Folgengliedern beliebig klein wird (siehe Bild). Dadurch lassen sich vor allem die reellen Zahlen [math] \mathbb{R}[/math] konstruieren, wie hier gezeigt werden soll. Cauchy-Folgen sind benannt nach dem französischen Mathematiker Augustin Louis Cauchy (1789-1857) der den Weg zur modernen Analysis mit bereitet hat. Zudem wird hier behandelt, wo die reellen Zahlen auftauchen und wie sie konstruiert werden können.
Bevor die Cauchy-Folge erklärt wird, betrachten wir aber das Heron-Verfahren, da wir hieran gut die Besonderheiten der reellen Zahlen sehen können.
Augustin-Louis Cauchy
Cauchy war ein sehr wichtiger Entwickler auf dem Gebiet der Analysis im frühen 19.Jahrhundert. In den 1820er-Jahren hat er das gesamte Gebiet der Reellen Analysis umgekehrt, indem er die Begriffe Grenzwert, Stetigkeit, Ableitung und Integral formuliert hat. Darüber hinaus hat er die Komplexe Analysis entwickelt. Deshalb sind heute viele Ergebnisse auf diesem Gebiet mit seinem Namen behaftet. Daneben führte Cauchy die erste sogenannte Revolution der Strenge in der Mathematik ein.
Augustin-Louis Cauchy wurde am 21.August 1789 geboren, also mitten in die französische Revolution hinein. Noch vor dieser war sein Vater ein hoher Beamter. Im Jahr 1794, als die Revolution bereits im Gang war, floh er mit seiner Familie in den kleinen Ort Arcueil und lebte dort abgeschieden. Ganz stark geprägt wurden die Kinder durch das Ausleben einer tiefen Religiosität, die sie auch später noch begleiten sollte. Die Ausbildung von Cauchy übernahm sein Vater, da er klassische Sprachen und Literatur selbst ausgezeichnet beherrschte. Schon hier zeigte sich aber beim Sohn ein ganz anderes besonderes Talent, nämlich das für Mathematik.
Zufällig hatte nun auch Joseph-Louis Lagrange ein Anwesen in Arcueil, sodass Cauchy sowohl ihm als auch anderen Wissenschaftlern, die bei Lagrange zu besuch waren, begegnen konnte.Lagrange war beeindruckt von den Fähigkeiten des jungen Mannes und deshalb auch interessiert an seiner Ausbildung. Zwei Jahre später kehrte die Familie nach Paris zurück, wo der Vater seine Karriere unter dem neuen Regime fortsetzen konnte und nun zum Generalsekretär des Senats - dessen Kanzler wiederum Laplace war - bestimmt wurde. Zuerst besuchte Cauchy eine humanistische Schule, bevor er 1805 an der Aufnahmeprüfung zur École Polytechnique teilnahm. Dort belegte er den zweiten Platz und nahm mit 16 Jahren das Studium an dieser Schule auf. Nach zwei Jahren Ausbildung mit Schwerpunkt auf Mathematik und Mechanik wechselte er zur École des Ponts et Chaussées für zwei Jahre und war 1810 mit nicht ganz 21 Jahren bereits Ingenieur. Dann ging er nach Cherbourg zum Aufbau des dortigen Hafens, der zu dieser Zeit eine große strategische Bedeutung für Militäroperationen gegen Großbritannien hatte. Hier entstanden erste mathematische Arbeiten zu sehr vielen Themen wie der Theorie der Brücken, den Polyedern oder den figurierten Zahlen. In Cherbourg blieb Cauchy fast drei Jahre, unter anderem weil seine Arbeit sehr gelobt wurde. Daneben beschäftigte er sich in seiner knappen Freizeit noch mit mathematischer Forschung. Im Selbststudium eignete er sich selbst Werke von Lagrange (Traité des fonctions analytiques) und Laplace (Mécanique céleste) an. Seine mathematische Karriere begann 1811, als es ihm gelang ein Problem von Lagrange zu lösen. Um eine Krankheit auszukurieren, ging Cauchy 1812 für einige Zeit nach Paris zurück, wo er schließlich das Manuskript einer Arbeit über symmetrische Funktionen vervollständigte, die bereits jene grundlegenden Ideen enthielt, aus der später die Gruppentheorie hervorgehen sollte. In dieser Arbeit, die dann 1815 veröffentlicht wurde, benutzte er zum einen Methoden von Gauß, zum anderen aber auch neue Methoden um zahlentheoretische Resultate von Lagrange und Ruffini zu verallgemeinern. Zudem entwickelte er darin die Theorie der Determinanten.
Mittlerweile war Cauchys Interesse an der Ingenieurstätigkeit erloschen, und er wollte sich nun ganz der Mathematik widmen; deshalb versuchte er, eine Stelle in Paris zu bekommen, allerdings erfolglos. Unterdessen schrieb Cauchy eine Arbeit, in der er versuchte, die Anzahl der reellen Nullstellen einer algebraischen Gleichung vorherzubestimmen - ein Gebiet, mit dem er sich immer wieder beschäftigen sollte. Hohe Reputation erlangte er dann mit einer Abhandlung zur Berechnung bestimmter Integrale. Hier zeigte sich bereits die mathematische Vielseitigkeit von Cauchy, die er im Laufe seines Lebens entwickelte. Im Laufe seines Lebens veröffentlichte er sieben Bücher und mehr als 800 wissenschaftliche Arbeiten.
Nachdem mehrere Versuche, in die Akademie der Wissenschaften gewählt zu werden, erfolglos geblieben waren, wurde Cauchy, der Royalist war, nach der Machtübernahme der Bourbonen im Jahr 1816 letztlich zum Mitglied der Akademie bestimmt, statt gewählt. Dieser Erfolg kostete ihn jedoch die Freundschaft einiger Leute, da im Gegenzug zum Beispiel Monge und Carnot aus der Akademie ausgeschlossen wurden. Kurze Zeit später wurde Cauchy zum Professor an der École Polytechnique für Analysis und Mechanik ernannt. Bei den Studenten war Cauchy beliebt, er galt als unermüdlich, gutmütig und geduldig erklärend. Allerding beschwerten sich einige Studenten über seine Zeit-Überziehung sowie über seine royalistischen Ansichten.
In seinen Vorlesungen entwickelte er ferner einen neuen Strengebegriff in der Analysis. Zu dieser Zeit war der Begriff der Funktion nämlich noch schwammig, denn es wurde mit unendlichen Summen gerechnet, ohne sich die Frage nach deren Konvergenz zu stellen, was dann einige Paradoxien hervorrief. Außerdem waren die grundlegenden Begriffe des Integrals und der Ableitung noch nicht genau definiert worden. In seinem aus Vorlesungen hervorgehenden Werk Analyse algébrique befasste sich Cauchy mit all diesen grundlegenden Problemen der Analysis. Er lieferte eine exakte Definition des unendlich Kleinen, wozu er den Begriff des Grenzwertes mit etwa den Orten einführte, wie sie auch heute noch verwendet werden. Damit konnte er dann relativ leicht Folgen definieren und davon ausgehend zur genauen Definition von Ableitung und Integral weiter schreiten. Ähnliche Fortschritte hatte zeitgleich der böhmische Mathematiker Bolzano in Prag erzielt.
Weiterhin kann man sagen, dass Cauchy den Begriff der Konvergenz von unendlichen Summen einführte und zudem Kriterien fand, mit deren Hilfe man über die Konvergenz von unendlichen Summen Aussagen treffen kann. Dabei entwickelte Cauchy die Infinitesimalrechnung aus dem Mittelwertsatz, der seit Lagrange bekannt war. Zu der von Cauchy eingeführten mathematischen Strenge erzählt die Überlieferung, dass Laplace, als Cauchy sein Werk während eines wissenschaftlichen Treffens präsentierte, schleunigst nach Hause eilte und sich dort so lange einschloss, bis er alle seine unendlichen Summen, die er in seiner Himmelsmechanik verwendet hatte, überprüft hatte. Glücklicherweise hielten tatsächlich alle seiner unendlichen Summen dem Cauchyschen Konvergenztest stand.
In seinen wissenschaftlichen Forschungsarbeiten war Cauchy weniger streng. Zum Beispiel hielt er es nie für nötig, für seine von ihm verwendeten Funktionen Stetigkeit nachzurechnen, immerhin ein Begriff, den er selbst streng definiert hatte.
Interessanterweise hatte Cauchy sogar Pläne, die Lehrinhalte an der École Polytechnique zu reformieren. Mit seinem Cours d´Analyse strebte er die selbe Strenge an, die die Geometrie zu dieser Zeit schon hatte. Diese scheiterten jedoch zum großen Teil. Denn es gab Einwände, sie seien zu sehr theoretisch orientiert und überambitioniert. Schließlich wolle man ja Ingenieure ausbilden und keine Mathematiker.
Diese Zeit, also während der Restauration, war die fruchtbarste Schaffensperiode für Cauchy. Nun fixierte er sich auf vier Themenbereiche. Der erste war die Lehrtätigkeit, mit Schwerpunkt auf theoretischer Mechanik und Analysis. Daraus gingen die bereits beschriebenen fundamentalen Definitionen hervor. Der zweite war die mathematische Physik. Daraus resultierten wiederum zwei große Arbeiten über die Theorie der Wellenausbreitung und über die Elastizitätstheorie. Und drittens entwickelte Cauchy nahezu im Alleingang das bahnbrechende neue Gebiet der komplexen Analysis, das erst langsam an Anerkennung gewann, später aber gewaltige Auswirkungen haben sollte. Außerdem schuf er eine detaillierte Ausarbeitung der Theorie der Differentialgleichungen. Dabei erkannte er die Notwendigkeit, Existenzbeweise von Lösungen führen zu müssen. 1816 erhielt er einen Preis der Pariser Akademie für seine Lösung eines Problems der Hydromechanik.
All das schaffte Cauchy, bevor er 28 Jahre alt war. Aufgrund seiner hohen Produktivität würde auch eine ausführliche Aufzählung der Errungenschaften Cauchys jeden Rahmen sprengen. Hier nur einige Sätze und Begriffe aus der Mathematik, die seinen Namen tragen: Cauchysche Abschätzungsformel, Cauchysche Anfangswertprobleme, Cauchysche Integralformel, Cauchyscher Integralsatz, Existenzsatz von Cauchy, Cauchy-Riemannsche partielle Differentialgleichungen, Cauchy-Bunjakowsji-Schwarzsche-Ungleichung, Cauchysches Quotientenkriterium, Cauchy-Reihenproduktsatz, Cauchysches Wurzelkriterium und Cauchy-Folge, um die es hier besonders gehen soll.
1818 heiratete Cauchy und pflegte nun auch in seiner eigenen Familie die religiöse Tradition, die ihm zu Hause mitgegeben worden waren. Lange Zeit später, von 1830 an, änderte sich sein Leben von Grund auf. Nach der Revolution von 1830 ging Cauchy freiwillig ins Exil. Damit gab er seiner Verbundenheit mit dem gestürzten Bourbonenkönig Karl X. Ausdruck. Zuerst siedelte Cauchy in die Schweiz über, arbeitete dann von 1831 bis 1833 in Turin. Danach wurde er von Karl X. für fünf Jahre als Erzieher in den Bourbonen Exil-Ort Prag geholt. Cauchy hielt allerdings während dieser Zeit immer Kontakt zu den französischen Wissenschaftsinstitutionen. Schließlich wurde im Jahr 1835 in Paris die Zeitschrift Comptes Rendues der Akademie der Wissenschaften ins leben gerufen, die Cauchy mit vielen ausgedehnten Arbeiten geradezu überflutete. Seinetwegen wurde später sogar ein Seitenlimit von vier Seiten pro Arbeit eingeführt. Manchmal reichte Cauchy auch unvollständige Arbeiten ein, oder gar mehrere unfertige Skizzen zu einer Problematik, teilweise sogar ohne zu einem Ergebnis zu gelangen. Wegen seiner hohen Zahl an Publikationen schließlich würdigte man seine Arbeit in Paris sehr. Aufgrund seiner Selbstbezogenheit aber, seiner Unduldsamkeit gegenüber jüngeren Kollegen und nicht zuletzt aufgrund seiner religiösen und politischen Ansichten war Cauchy als Person nicht nur beliebt. Trotz allem war er in seinen Gutachten der Arbeiten anderer äußerst fair, würdigte deren Verdienste und gab auch eigene Fehler zu.
Schließlich kehrte er 1838 nach Paris zurück. Da Cauchy es ablehnte, einen Treueid auf die Regierung abzuleisten, konnte er zunächst keine Anstellung bekommen. Dann wurde er 1839 in das Bureau des Longitudines, das Amt für Maße und Gewichte, gewählt. Dort wurde er zwar von der Regierung nicht offiziell bestätigt, aber auch nicht wieder entfernt. Mit der Revolution von 1848 wurde der Treueid dann abgeschafft, so dass paradoxerweise gerade die liberalen Kräfte dem Royalisten Cauchy wieder eine legale Anstellung ermöglichten.
Cauchy griff zwar nie in die Politik ein, jedoch benutzte ihn die Kirche oft als Aushängeschild für ihre Ziele. So sollte er ein Beispiel für die Verknüpfung von Glaube und Wissenschaft sein, also eine auf der Vernunft basierende Bestätigung der Richtigkeit der kirchlichen Politik. Während eines Besuchs in Paris sagte Abel in diesem Zusammenhang über Cauchy: "Cauchy ist extrem katholisch und bigott. Das ist eine sehr seltsame Sache bei einem Mathematiker."
1857 erkrankte Cauchy, woraufhin ihm der Pariser Kardinal die Letzte Ölung erteilte. Am 23.Mai 1857 starb er.
Heron-Verfahren
Das Heron-Verfahren war schon den Babyloniern von vor 4000 Jahren bekannt, daher wird es auch als Babylonisches Wurzelziehen bezeichnet. Dabei wird die Wurzel von x anhand der Formel [math]a_{n+1}:=\frac{1}{2}(a_n+\frac{x}{a_n})[/math] approximiert. Dabei ist es egal, welcher Startwert [math] a_0 [/math] gewählt wird. Ein Beispiel zeigt:
Wurzel von 2:
[math] a_0 = 1 [/math]
[math] a_1 = [/math] 1/2(1 + 2/1) = 1,5
[math] a_2 = [/math] 1/2(1,5 + 2/1,5) = 1,4166666...
[math] a_3 = [/math] 1/2(1,41666667 + 2/1,41666667) = 1,41421143847...
...
[math] a_8 = [/math] 1,4142135624...
Zum Vergleich mit dem Startwert [math] a_0=3 [/math]
[math] a_0 = 3 [/math]
[math] a_1 = [/math] 1/2(3 + 2/3) = 1,833333...
[math] a_2 = [/math] 1/2(1,833333 + 2/1,833333) = 1,4621212105
...
[math] a_8 = [/math] 1,4142135624...
Eine geometrische Interpretation des Heron-Verfahrens ist die folgende: Gesucht ist die Seitenlänge eines Quadrats mit Flächeninhalt [math] x [/math]. Dazu wird zunächst ein Rechteck konstruiert, von dem bekannt ist, dass die Fläche [math] x [/math] beträgt (z.B. mit einer Seite der Länge [math] x_0=x [/math] und einer Seite der Länge [math] y_0=1 [/math]). Nun wird schrittweise mittels des Algorithmus des Heron-Verfahrens der Wert [math] x_i [/math] angepasst und [math] y_i=\frac{x}{x_i} [/math] gesetzt. Dieses Verfahren wird bis zur gewünschten Genauigkeit fortgeführt.
Zahlen
Wichtige Sätze der Analysis beruhen auf der Vollständigkeit von [math] \mathbb{R} [/math]
Bei der Einführung der Zahlensysteme kann man so vorgehen, dass man mit den natürlichen Zahlen [math]\mathbb{N}[/math] beginnt. Als Differenzen von natürlichen Zahlen erhält man die ganzen Zahlen [math]\mathbb{Z}[/math], als Quotienten von ganzen Zahlen die rationalen Zahlen [math]\mathbb{Q}[/math]. In [math]\mathbb{Q}[/math] kann man jetzt schon recht gut Analysis betreiben, etwa den Konvergenzbegriff einführen. Die Folge [math](\frac{1}{n})_{n\in\mathbb{N}}[/math] ist zum Beispiel aus [math]\mathbb{Q}[/math] und konvergiert gegen die Null.
Es gibt aber auch andere Folgen in [math]\mathbb{Q}[/math], die sich wie konvergente Folgen verhalten, deren Grenzwert aber nicht in [math]\mathbb{Q}[/math] liegt. Ein Beispiel dafür ist die Folge, die beim Heron-Verfahren zur Approximation von [math]\sqrt{2}[/math] konstruiert wird. Beschränkt man sich nur auf [math]\mathbb{Q}[/math], so ist eine solche Folge nicht konvergent, denn sie besitzt keinen Grenzwert in [math]\mathbb{Q}[/math], ist aber dennoch eine Cauchyfolge.
Beispiel: Wir berechnen die Cauchy-Folgeneigenschaft der Folge aus dem Heron-Verfahren nach. Die Folge ist definiert durch [math]a_0=2, a_n=1/2(a_{n-1} + 2/(a_{n-1})), n\in \mathbb{N}[/math].
Mittels vollständiger Induktion zeigt man, dass [math] a_n \in [1,2] \text{ für alle } n\in \mathbb{N}_0[/math] gilt. Weiterhin folgt
[math]a_{n+1} - a_n = 1/2 ( a_n + 2/a_n - a_{n-1} -2/a_{n-1}) = (1/2 - 1/(a_n * a_{n-1}))(a_n - a_{n-1})[/math] für [math] n \in \mathbb{N}[/math]. Somit ergibt sich:
[math] |a_{n+1} - a_n|\leq 1/2 |a_n - a_{n-1}| \leq (1/2)^n |a_1 - a_0| [/math]
Für [math]m\gt n[/math] folgt mit der geometrischen Reihe: [math] |a_m - a_n|\leq \sum\nolimits_{k=n}^{m-1} |a_{k+1} - a_k|\leq \sum\nolimits_{k=n}^{m-1} (1/2)^k|a_1 - a_0| = (1/2)^n|a_1 - a_0| \sum\nolimits_{k=0}^{m-n-1} (1/2)^k \leq (1/2)^{n-1}|a_1 - a_0|[/math]
Indem wir n groß genug wählen, wird die Schranke auf der rechten Seite kleiner als jedes vorgegebene [math]\varepsilon\gt 0[/math]. Wir haben damit den Nachweis erbracht, dass [math](x_n)_{n\in\mathbb{N}} [/math] eine Cauchy-Folge ist.
Wichtige vorbereitende Definitionen und Sätze
Definition 1: Eine Folge [math](a_n)_{n\in\mathbb{N}}[/math] heißt Nullfolge, wenn [math]\lim_{n\to\infty} a_n = 0[/math] gilt.
Definition 2: Eine Folge [math](a_n)_{n\in\mathbb{N}}[/math] heißt Fundamentalfolge oder Cauchy-Folge, wenn gilt: [math] \forall \varepsilon\gt 0 , \exists n_1 \in \mathbb{N} : d(a_n,a_m)\lt ε , \forall n,m\geq n_1[/math].
Definition 3: Die Anordnungsaxiome: Ein angeordneter Körper ist ein Körper K zusammen mit einer Teilmenge [math]P \subset K[/math]. Diese erfüllt folgende Ordnungsrelationen oder Anordnungsaxiome:
O1 Für jedes [math]a \in K [/math]gilt genau eine der folgenden Aussagen:
| i) | [math]a\in P[/math] | a>0 |
| ii) | a = 0 | a = 0 |
| iii) | [math]-a\in P[/math] | -a>0 |
O2
| [math]a,b\in P \Rightarrow a+b, ab \in P[/math] |
| [math]a,b \gt 0 \Rightarrow a+b\gt 0 \land ab\gt 0 [/math] |
Definition 4: Es sei M eine Teilmenge des angeordneten Körpers K. Ein Element [math]s\in K[/math] heißt Supremum vom M, falls gilt:
- s ist eine obere Schranke von M
- Ist t eine obere Schranke von M, so folgt: [math] t \geq s [/math]
D.h. s ist die "kleinste obere Schranke" von M.
Eine Folge reeller Zahlen ist eine Abbildung [math] f:\mathbb{N} \to \mathbb{R} [/math]. Wir schreiben [math] f=(a_n)_n \in \mathbb{N} [/math].
Definition 5: Wir sagen, dass eine Folge [math] f:\mathbb{N} \to K [/math]konvergiert, wenn ein [math] a\in K [/math] existiert, sodass für alle [math]\varepsilon \gt 0 [/math] ein [math] N_0\in\mathbb{N} [/math] existiert, sodass [math] |a_n-a| \lt \varepsilon [/math] für alle [math] n\geq N_0 [/math]. Wir nennen [math] a [/math] dann den Limes der Folge und schreiben [math] a=lim_{n\to \infty} a_n [/math].
Satz: Jede konvergente Folge ist eine Cauchy-Folge.
Beweis: Ist [math]\varepsilon \gt 0 [/math] vorgegeben, so ist auch [math]\frac{\varepsilon}{2} \gt 0 [/math] und es gibt wegen der Konvergenz ein [math] N_0[/math], sodass [math]|a-a_n| \lt \frac{\varepsilon}{2}, \forall n \geq N_0[/math]. Dann gilt wegen der Dreiecksungleichung [math]|a_n-a_m|=|(a_n - a)+(a-a_m)|\leq |a-a_n|+|a-a_m|\lt \frac{\varepsilon}{2} + \frac{\varepsilon}{2} = \varepsilon , \forall n,m\geq N_0[/math]. Die Umkehrung gilt nicht in [math]\mathbb{Q}[/math]! (Aber in [math]\mathbb{R} \lor \mathbb{C}[/math])
Wir wollen nun [math]\mathbb{Q}[/math] so erweitern/ vervollständigen, dass in der vervollständigten Menge jede Cauchy-Folge konvergiert. Einen Raum mit dieser Eigenschaft nennt man vollständig. Die Vervollständigung von [math]\mathbb{Q}[/math] heißt vollständige Hülle von [math]\mathbb{Q}[/math].
Konstruktion der vollständigen Hülle von [math]\mathbb{Q}[/math]
Man könnte zunächst daran denken, die Cauchy-Folgen selbst als Elemente der zu konstruierenden Menge zu verwenden. Doch zeigt schon die Betrachtung konvergenter Cauchy-Folgen, dass es jeweils beliebig viele Folgen mit gleichem Grenzwert (Limes) gibt. Sind [math](a_n)_{n\in\mathbb{N}} [/math] und [math](b_n)_{n\in\mathbb{N}} [/math] zwei solcher Folgen, so ist allerdings [math](a_n-b_n)_{n\in\mathbb{N}} [/math] eine Nullfolge. Dies führt zu einer Klasseneinteilung in der Menge aller Cauchy-Folgen durch die Einführung einer Äquivalenzrelation: Zwei Folgen werden genau dann miteinander identifiziert, wenn ihre Differenz eine Nullfolge ist. Man prüft leicht nach, dass dies in der Tat eine Äquivalenzrelation ist. Wir bezeichnen nun den Abschluss von [math]\mathbb{Q}[/math] nun als [math]\mathbb{\bar Q}[/math]. Damit kann man [math]\mathbb{\bar Q}[/math] anordnen und einen Absolutbetrag einführen, durch den in [math]\mathbb{\bar Q}[/math] eine Metrik und damit eine topologische Struktur eingeführt werden kann, durch die [math]\mathbb{\bar Q}[/math] die Eigenschaften einer topologischen Gruppe erhält. Es zeigt sich, dass jede Cauchy-Folge in [math]\mathbb{\bar Q}[/math] konvergiert. [math]\mathbb{\bar Q}[/math] ist die gesuchte vollständige Hülle von [math]\mathbb{Q}[/math].
Einbettung von [math]\mathbb{Q}[/math] in [math]\mathbb{\bar Q}[/math]
Die Abbildung [math] \iota: \mathbb{Q}\to \mathbb{\bar Q} [/math] definiert durch [math] \iota(p)=[(p,p,p,\dots)][/math] ist eine injektive strukturverträgliche Abbildung. Strukturverträglichkeit bedeutet hier Verträglich mit der Gruppenstruktur von ([math]\mathbb{Q}[/math],+) und der topologischen Struktur.
Aus der Konstruktion von [math]\mathbb{\bar Q}[/math] ergibt sich auch die universelle Eigenschaft von [math] \iota [/math]. Denn ist M irgendeine Menge mit den geforderten Strukturmerkmalen (d.h. Jede Cauchy-Folge ist konvergent), und lässt sich [math]\mathbb{Q}[/math] in M einbetten durch die strukturverträgliche Abbildung [math]f:\mathbb{Q} \to M[/math], so kann zunächst gefolgert werden, dass [math](f(a_n))[/math] eine Cauchy-Folge in M ist, wenn [math](a_n)[/math] eine Cauchy-Folge in [math]\mathbb{Q}[/math] ist. [math](f(a_n))[/math] konvergiert wegen der Struktureigenschaften von M dann gegen ein Element [math]r' \in M[/math]. Die Abbildung [math]g:\mathbb{\bar Q} \to M[/math] definiert durch [math]g([a_n])= r'[/math] bettet dann [math]\mathbb{\bar Q}[/math] in M ein, und es ist [math]f = g \circ i[/math]. [math]\mathbb{\bar Q}[/math] ist damit die kleinste [math]\mathbb{Q}[/math] umfassende Menge, in der jede Cauchy-Folge konvergiert, und ist bis auf Isomorphie eindeutig bestimmt.
Isomorphie von [math]\mathbb{\bar Q}[/math] und [math]\mathbb{R}[/math]
Die Isomorphie von [math]\mathbb{\bar Q}[/math] und [math]\mathbb{R}[/math] ist selbsterklärend da [math]\mathbb{\bar Q}[/math] und [math]\mathbb{R}[/math] gleich definiert sind. Dies folgt also daraus, dass gezeigt wurde, dass [math]\mathbb{\bar Q}[/math] die kleinste [math]\mathbb{Q}[/math] umfassende Menge ist, die die Bedingungen der Cauchy-Folge erfüllt. Denn aus dem Stetigkeitsbegriff(3.Eigenschaften) wissen wir, dass der Grenzwert einer gegen [math]\sqrt{2}[/math] konvergierenden Folge in [math]\mathbb{Q}[/math] nicht existiert, aber dafür in [math]\mathbb{\bar Q}[/math], da dies die kleinste Hülle ist, die [math]\mathbb{Q}[/math] umschließt und somit den Dichtheitsbegriff (2.Beispiele) erweitern und stetige Funktionen auf [math]\mathbb{\bar Q}[/math] zulassen. Die topologische Struktur von [math]\mathbb{\bar Q}[/math] heißt reelle Topologie im Unterschied zur sogenannten rationalen Topologie von [math]\mathbb{Q}[/math]. Durch [math][(a_n)]*[(b_n)]:=[(a_n * b_n)][/math] und [math][(a_n)]^{-1} :=[a_n^{-1}][/math] für [math]a_n \neq 0[/math] lässt sich die algebraische Struktur von [math]\mathbb{\bar Q}[/math] zu einer Körperstruktur derart erweitert, dass [math]\mathbb{R}[/math] und [math]\mathbb{\bar Q}[/math] bijektiv unter Erhaltung aller Strukturmerkmale aufeinander abgebildet werden können.[1]
Wir bezeichnen fortan [math]\mathbb{\bar Q}[/math] als [math]\mathbb{R}[/math].
Cauchy-Folge
Sei C die Menge der Cauchy-Folgen auf [math]\mathbb{Q}[/math].
Eigenschaften von Cauchy-Folgen
Seien [math] (x_n)_{n\in\mathbb{N}},(y_n)_{n\in\mathbb{N}} \subset C [/math]. Dann gilt:
a) [math] (x_n)_{n\in\mathbb{N}} [/math] ist beschränkt.
b) [math] (x_n + y_n)_{n\in\mathbb{N}} \subset C[/math]
c) [math] (x_n * y_n)_{n\in\mathbb{N}} \subset C[/math]
d) Ist [math](x_n)_{n\in\mathbb{N}} [/math] keine Nullfolge [math]\Rightarrow \exists ε\gt 0, ε\in\mathbb{Q}, N\in\mathbb{N}[/math], sodass entweder [math]x_n\geq ε, \forall n \geq N[/math] oder [math]x_n\leq -ε, \forall n \geq N[/math], die die Axiome O1 und O2 erfüllen. Statt [math]a \in P[/math] schreiben wir a>0, sprich: "a positiv".
e) Ist [math] (x_n)_n\in\mathbb{N} [/math] keine Nullfolge, [math]x_n\neq 0, \forall n\in \mathbb{N} \Rightarrow (x_n^{-1})\in C [/math]
Man kann die Cauchyfolgen-Eigenschaft (siehe Definition) in vollständigen metrischen Räumen verwenden ohne Kenntnis über den Grenzwert zu haben. Folgende Konvergenzkriterien gibt es (werden aber nicht unbedingt erklärt, da sie nicht von besonderer Wichtigkeit hier sind): Majorantenkriterium, Einschließungskriterium, Monotoniekriterium, Bolzano-Weierstraß, Cauchy-Kriterium (Eine reelle Zahlenfolge konvergiert genau dann gegen eine reelle Zahl, wenn sie eine Cauchy-Folge ist. Es gilt: [math](a_n)_{n\in\mathbb{N}}[/math] ist Cauchy-Folge [math]\Leftrightarrow (a_n)_{n\in\mathbb{N}}[/math] ist konvergent. Dieses Kriterium gilt wie oben erwähnt zum Beispiel in [math]\mathbb{R}[/math], aber nicht in [math]\mathbb{Q}[/math].)
Jede Cauchy-Folge in [math]\mathbb{R}[/math] ist konvergent. Dieser Satz lässt sich mit dem Satz von Bolzano Weierstraß zeigen. Diese Implikation gilt nicht in [math] \mathbb{Q} [/math] (wie oben bereits am Beispiel der Folge mit Grenzwert [math] \sqrt{2} [/math] gezeigt). Dies ist ein substantieller Unterschied zwischen den rationalen und den reellen Zahlen: Die reellen Zahlen sind vollständig, die rationalen hingegen nicht. (Wir nennen einen normierten Raum vollständig, wenn jede Cauchy-Folge konvergiert.)
Die Vollständigkeit der Reellen Zahlen muss man bei der Definition dieser durch ein Axiom, also eine nicht beweisbare Voraussetzung, verankern. Dazu gibt es verschiedene Vollständigkeitsaxiome, die verwendet werden können: Dedekindsche Schnitte, Intervallschachtelung, Cauchy-Kriterium, Satz von Bolzano-Weierstraß,...
Konstruktion über Cauchy
Konstruktion der Menge [math]\mathbb{R}[/math] als Körper
Zwei Cauchy-Folgen [math] (x_n)_n\in\mathbb{N},(y_n)_n\in\mathbb{N} [/math] heißen äquivalent [math] (x\sim y)[/math], falls [math] x_n - y_n \to 0[/math].
Wir definieren nun [math]\mathbb{R}[/math] als die Menge dieser Äquivalenzklassen.
Eigenschaften:
a) ([math]\mathbb{R}[/math], +) ist eine abelsche Gruppe
b) ( [math]\mathbb{R}[/math]\{0}, * ) ist eine abelsche Gruppe
c) Es gilt das Distributivgesetz
d) ([math]\mathbb{R}[/math], +, *) ist ein Körper
Quellen
- Mathematik, Springer-Spektrum, ISBN: 978-3-662-56740-1, S.190, 1053, 1173
- Höhere Mathematik, Verlag Harri Deutsch, ISBN: 978-3-8171-1872-4, S.345, 351, 388
- Grundwissen Mathematikstudium, Springer-Spektrum, ISBN: 978-3-8274-2308-5, S.297, 772
- Lexikon der Mathematik BAND:1, Spektrum Akademischer Verlag, ISBN: 978-3-662-53498-4, S.292ff.
- Springer-Taschenbuch der Mathematik, Springer-Spektrum, ISBN: 978-3-8351-0123-4, S.243
- dtv-Atlas der Mathematik Band 1, Dtv, ISBN: 978-3-423-03007-6, S.61
- Rechnen und Mathematik, Bertelsmann Lexikon-Verlag, Buch-Nr. 1599'1180, S.447
- Die bedeutendsten Mathematiker, matrixwissen, ISBN: 978-3-86539-916-8, S.107ff.
- https://www.mathematik.de/algebra/179-erste-hilfe/zahlenbereiche/reelle-zahlen/2441-cauchy-folgen
Bildnachweis
- http://mathphys-online.de/heronverfahren-numerische-berechnung-von-quadratwurzeln/#prettyPhoto
- https://www.kapiert.de/reelle-zahlen-zahlenbereiche-untersuchen
- https://en.wikipedia.org/wiki/Augustin-Louis_Cauchy
- https://www.haufe-lutz.de/detail/99903BB/ (Stand 18.09.21/da Onlineshop)
- https://www.mathematik.de/algebra/179-erste-hilfe/zahlenbereiche/reelle-zahlen/2441-cauchy-folgen
Weiterführende Literatur
- Abhandlung über bestimmte Integrale zwischen imaginären Grenzwerten (Oswalds Klassiker 112 (1900))
- [1] Mit Mathe richtig anfangen, Springer Spektrum, ISBN: 978-3-662-59230-4, S.225/Kapitel 5
- https://www.mathematik.de/algebra/179-erste-hilfe/zahlenbereiche/reelle-zahlen/2441-cauchy-folgen
- https://www.mathematik.de/
Autoren
- Alexander Fichtelmann
- Immanuel Klevesath