Anwendungen der Knotentheorie: Unterschied zwischen den Versionen
| (79 dazwischenliegende Versionen von 4 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | In diesem Artikel geht es darum, wie man mehr oder weniger alltägliche Probleme mithilfe der Kontentheorie beschreiben und sogar lösen kann. Wie nützlich die hier gezeigten Lösungen zu Problemen vom Schuhe schnüren über das Krawatte binden bis hin zum Bilder aufhängen ist, mag der geneigte Leser selbst entscheiden. | |
| + | == Grundlagen<ref>https://en.wikipedia.org/wiki/Knot_(mathematics)</ref> == | ||
| + | [[Datei:Reidemeisterbewegungen.jpg|mini|328x328px|Die drei Reidemeisterbewegungen]] | ||
| + | Ein Knoten ist mathematisch eine Einbettung des Kreises <math>S^1</math> in den dreidimensionalen euklidischen Raum <math>\mathbb{R}^3</math>. | ||
| + | Wir betrachten im Folgenden nur die reguläre Projektion eines Knotens in den zweidimensionalen Raum <math>\mathbb{R}^2</math>. Reguläre Projektionen sind solche, welche überall bis auf die Punkte der Kreuzungen injektiv sind und eine endliche Anzahl dieser Kreuzungspunkte besitzen. Zudem fordern wir, dass die Punkte an einer Kreuzung nicht kolinear sein dürfen, dass bedeutet ein Kreuzungspunkt ist kein Berührpunkt. | ||
| + | |||
| + | Die Projektion des Knotens ist nicht eindeutig. Zwei Projektionen gehören genau dann zum gleichen Knoten, wenn sie mithilfe einer Hintereinanderausführung von sogenannten Reidemeisterbewegungen ineinander überführt werden können. | ||
| + | Dabei ist es erlaubt eine Schlaufe zu bilden oder zu lösen (Bewegunstyp 1), sich überlappende Stränge in in parallel verlaufende umzuwandeln (Bewegungstyp 2) und den Strang über einer darunter liegenden Kreuzung zu verschieben (Bewegungstyp 3). | ||
| + | |||
| + | === Keltische Knoten und deren Darstellungen === | ||
| + | Ein keltischer Knoten ist ebenfalls eine wie schon zuvor definierte reguläre Projektion eines Knotens mit der zusätzlichen Einschränkung, dass sich für jeden Strang Über- und Unterkreuzungen stets abwechseln müssen.<ref>http://www.bilder-der-mathematik.de/picturebook/pages/picturebook_pages_100_101.pdf</ref> | ||
| + | |||
| + | Die reguläre Projektion eines Knotens ist graphentheoretisch ein sogenannter medialer Graph, zu dem wiederum ein planerer Graph gehört. <ref>https://en.wikipedia.org/wiki/Medial_graph</ref> Ein planerer Graph ist ein Paar <math>G=(V,E)</math>, mit der endlichen Menge der Vertices <math>V\neq\emptyset</math> und der ebenfalls endlichen Menge der Kanten <math>E\subseteq\lbrace\lbrace u,v\rbrace\lvert u,v\in V, u\neq v\rbrace</math>. | ||
| + | |||
| + | Die Darstellung des Knotens als planarer Graph, erhalten wir mithilfe der folgenden Schritte: | ||
| + | |||
| + | Wir betrachten zu Beginn den medialen Graphen und färben diesen zunächst schachbrettartig ein, indem wir die Fläche außerhalb des Graphen weiß färben und anschließend alle anderen durch die Kanten des Graphen abgegrenzten Flächen so färben, dass jede Kante eine weiße von einer schwarz gefärbten Fläche abtrennt. | ||
| + | |||
| + | [[Datei:Kreuzungsarten.jpg|mini|200x200px|Zur Veranschaulichung der verschiedenen Kanten]] | ||
| + | |||
| + | Anschließend definieren wir in jeder schwarz gefärbte Fläche einen Vertex des planaren Graphen und verbinden diese über die Kreuzungen des medialen Graphen mit den angrenzenden Vertices. | ||
| + | |||
| + | Damit die Information erhalten bleibt, wie sich die Stränge an den Kreuzungspunkten über- oder unterkreuzen, kennzeichnen wir die Kanten auf zwei unterschiedliche Weisen: | ||
| + | |||
| + | Falls die Fläche links neben dem überkreuzenden Strang schwarz ist kennzeichnen wir dies mit einer durchgezogenen Kante. Dabei ist es wichtig dem Verlauf des Strangs in Richtung der Kreuzung zu folgen. | ||
| + | |||
| + | Falls hingegen die schwarze Fläche rechts neben dem obenliegenden Strang liegt, so wird die neue Kante des planaren Graphen gestrichelt.<ref>http://www.entrelacs.net/Die-Grundlagen</ref> <gallery widths="150" heights="150"> | ||
| + | Datei:Blauer Knoten.jpg|reguläre Projektion eines Knotens, bzw. dessen medialer Graph | ||
| + | Datei:Knoten-Graph mit schraffierten Flächen.jpg|Schachbrettartige Schraffierung und eingezeichnete Vertices des planaren Graphen | ||
| + | Datei:Knoten und Graph.jpg|Verbindung der Vertices mit den entsprechenden Kanten zu einem planaren Graphen | ||
| + | Datei:Knoten Graph.jpg|Der zugehörige Planare Graph | ||
| + | </gallery> | ||
| + | |||
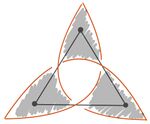
| + | [[Datei:Planarer und medialer Graph.jpg|mini|Zwei zueinander isomorphe Planare Graphen (grau) und deren zugehörige mediale Graphen (rot), dabei wurde hier an den Vertices zur Vereinfachung die Über- und Unterkreuzungen noch nicht beachtet (-> siehe Kleeblattknoten)|alternativtext=|200x200px]] | ||
| + | |||
| + | Umgekehrt existiert auch der inverse Prozess und es kann aus einem solchen planaren Graph der zugehörige mediale konstruiert werden (Allerdings sei angemerkt, dass zueinander isomorphe planare Graphen nicht zwingend zueinander isomorphe mediale Graphen besitzen). | ||
| + | |||
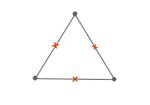
| + | Hierfür zeichnen wir in die Mitte jeder Kante ein Kreuz, welches anschließend einen Vertex definiert. Für jede Fläche im planaren Graphen (dazu gehört etwa auch die Fläche außerhalb des Graphen) werden benachbarte Kreuze bzw. neue Vertices, also solche zwischen denen im planaren Graph nur eine Ecke ist, miteinander verbunden. Insbesondere werden Ecken auch innerhalb einer Fläche doppelt verbunden, wenn sie zweifach benachbart sind. Entsprechend der Art der Kante (durchgezogen/gestrichelt) und nach Schachbrettmusterung wie im vorigen Abschnitt beschrieben ist an den Kreuzungspunkten festgelegt, welcher Strang über- und welcher unterkreuzt. | ||
| + | |||
| + | Auf diese Art lassen sich sehr einfach keltische Knoten konstruieren. Es sei angemerkt, dass die Eigenschaft des abwechselnden Über- und Unterkreuzens dann gewährleistet ist, wenn der planare Graph entweder nur aus durchgezogenen (linkskreuzenden) oder nur aus gestrichelten (rechtskreuzenden) Kanten besteht. | ||
| + | |||
| + | <gallery widths="150" heights="150"> | ||
| + | Datei:Dreieck mit Kreuzen.jpg|Planarer Graph mit neuen Vertices des medialen Graphen | ||
| + | Datei:Graph planar-medial.jpg|Medialer Graph | ||
| + | Datei:Kleeblattknoten.jpg|Fertiger Kleeblattknoten, bzw. dessen medialer Graph | ||
| + | </gallery> | ||
| + | |||
| + | == <ref>http://export.arxiv.org/pdf/1401.8242</ref>Die Mathematik des Krawattenbindens == | ||
| + | Krawatten sind seit Ludwig dem XIV als modisches Accesoire bekannt und seither müssen sich die Träger um einen Knoten bemühen, um ihre Krawatte zu befestigen. Auswahl gibt es genug, den einfachen Four-in-Hand, den (halben) Windsorknoten, den Cavendish-Knoten, den kleinen Knoten und viele mehr. | ||
| + | Die meisten dürften nicht sehr viele verschiedene Arten der Krawattenbefestigung kennen, dabei existieren 85 mögliche Knoten zum Binden einer Krawatte mit 8 Zügen, die allerdings nicht alle Balance, Symmetrie und Form berücksichtigen, wie der theoretische Physiker Thomas Fink und die Mathematikerin Yong Mao herausfanden <ref>https://en.wikipedia.org/wiki/The_85_Ways_to_Tie_a_Tie</ref>. Aus praktischen Gründen werden also nicht alle davon realisiert, zum Einen sind unendlich lange Krawatten leider noch nicht erfunden, zum Anderen müsste man dann eventuell einen sehr schweren, unförmigen Krawattenknoten um den Hals tragen und bekäme davon bestimmt Rückenschmerzen. | ||
| + | Dieser Gedanke lässt sich auch noch weiterführen. Wir wollen uns fragen, wie viele Möglichkeiten es gibt, eine Krawatte mit 13 Zügen zu binden, denn gerade schmale Krawatten werden häufiger umeinandergeschlungen und -gewickelt als breite <ref>http://export.arxiv.org/pdf/1401.8242</ref>. Diese Anzahl ergibt sich daraus, dass breite Krawatten gewöhnlicherweise 9 Mal binden lassen, während schmale maximal 15 Mal umeinander gewickelt werden. Um den Komfort zu erhalten, nehmen wir eine etwas kleinere Zahl als möglich an. | ||
| + | |||
| + | Zunächst führen wir eine Sprache ein, um eine Krawatte und ihren Knoten allgemein beschreiben zu können. Wir führen ein, dass wir immer ein aktives schmales Ende der Krawatte haben und das andere, breite Ende festhalten, damit es nicht verrutscht. Weiterhin teilen wir den Krawattenbinder in drei Regionen ein, die durch seine Krawatte eingeteilt werden, einen linken, einen rechten und einen zentralen Teil und bezeichnen sie mit <math> L </math>, <math> C </math> und <math>R</math> (left, center, right). | ||
| + | Wir schreiben <math>\odot</math>, wenn wir die den schmalen Teil der Krawatte "aus der Ebene hinaus" ziehen und <math>\otimes </math>, wenn wir den schmalen Teil der Krawatte "in die Ebene hinein" ziehen. Außerdem schreiben wir <math>U</math> dafür, wenn wir die schmale Seite der Krawatte durch eine zuvor entstandene Schlaufe ziehen, wie es am Ende eines jeden Krawattenknotens der Fall ist. Dies ist offensichtlich nur dann erlaubt, wenn wir die Krawatte im letzten Zug "aus der Ebene heraus" gezogen wurde. | ||
| + | Mit großen Symbolen beschreiben wir also jeweils die Lage des breiten Endes der Krawatte, wenn das schmale Ende sich um das Zentrum <math>C</math> schlingt, mit dem Index die Richtung, in der wir die Krawatte ziehen und <math>U</math> beschreibt eine Umwicklung, wie oben beschrieben. Somit erhalten wir die folgenden möglichen Bewegungen, die wir mit der Krawatte durchführen können: | ||
| + | <math>\{L_{\otimes}, L_{\odot}, C_{\otimes}, C_{\odot}, R_{\otimes}, R_{\odot}, U\}</math> | ||
| + | Um die Stabilität der Krawatte zu gewährleisten führen wir einige Regeln ein: | ||
| + | # <math>(L,C,R)</math> darf sich nicht wiederholen, d.h. gleiche Symbole dürfen nicht aufeinander folgen. <math>U</math> ist davon unabhängig und auch eine Folge aus <math>(LCR)U(LCR)</math> ist nicht erlaubt. | ||
| + | # <math>\otimes</math> und <math>\odot</math> dürfen sich nicht direkt wiederholen. <math>U</math> ist unabhängig davon. | ||
| + | # <math>U</math> darf nur direkt auf eine Bewegung nach außen folgen. | ||
| + | # Ein Knoten darf nur mit <math>C_{\otimes}, C_{\odot}, U</math> enden. | ||
| + | # Eine <math>k</math>-fache Umschlingung ist erst erlaubt, wenn zuvor <math>2k</math> andere Bewegungen ausgeführt wurden. | ||
| + | Wir können im Folgenden die Symbole <math>\otimes</math> und <math>\odot</math> direkt weglassen, da sich stets aus dem letzten rekonstruieren lässt, mit welcher Bewegung wir begonnen haben (die letzte Bewegung muss nach außen gehen, da wir den Knoten mit <math>U</math> beendet werden muss und Regel 3 erfüllt ist und außen und innen müssen sich stets abwechseln). Weiterhin können wir die Krawatte entweder im (<math>T</math>) oder gegen den Uhrzeigersinn (<math>W</math>) umschlingen, denn <math> RUR </math>, <math> CUC </math> und <math> LUL </math> können nicht auftreten wegen unserer ersten Annahme. Die Position des aktiven (schmalen) Teils der Krawatte lässt sich dann beschreiben als <math>\#W-\#T (mod 3)</math>. | ||
| + | Elementare Überlegungen führen uns auf die Tatsache, dass wenn wir den Krawattenknoten mit <math>W</math> begonnen haben gelten muss <math>\#W-\#T = 2 (mod 3)</math> und wenn wir den Knoten mit <math>T</math> begonnen haben gelten muss <math>\#T-\#W = 2 (mod 3)</math> für eine k-fache Umwicklung einer 2k-langen Sequenz. Hierbei fließt mit ein, dass die erste Bewegung die Schlaufe bildet, durch die das schmale Krawattenende zum Schluss gezogen wird. Gewöhnlicherweise muss die Krawatte von der Seite kommen, von der die Schlaufe kommt. Jede andere Schlaufe von links nach rechts oder rechts nach links muss vor oder hinter dem Knoten liegen und zwischen dem ersten und dem vorletzten liegen <math>2k-1</math> Umschlingungen. In diesen muss die Krawatte die Krawatte auf die richtige Seite gebracht werden und daraus folgt die oben aufgestellte Behauptung. | ||
| + | |||
| + | Nun wollen wir eine Grammatik aufbauen, die beschreibt, wie wir die Krawatte binden können. Hierfür verwenden wir die Backus-Naur-Form <ref>https://de.wikipedia.org/wiki/Backus-Naur-Form</ref>. Es handelt sich hierbei um eine kontextfreie Grammatik, die in der Informatik Anwendung findet. Dabei werden neue Symbole definiert, indem bereits bekannte Symbole durch Leer-, Zeilen- und Spaltentrennzeichen definiert werden. Hierdurch können Umschlingungsfolgen zusammengefasst werden. | ||
| + | |||
| + | Nun können wir für unseren Krawattenknoten unter Verwendung der oben erwähnten Grammatik Erzeugende Funktionen <ref>https://de.wikipedia.org/wiki/Erzeugende_Funktion</ref> finden, die sich durch eine formale Potenzreihe | ||
| + | <math> \begin{align}f(z) = \sum\limits_{n=0}^{\infty} a_nz^n \end{align}</math> | ||
| + | darstellen lassen. Mittels eines Computers und der zuvor definierten Grammatik lässt sich eine solche Erzeugenden Funktion finden. So wird ein einfacher Krawattenknoten beschrieben durch | ||
| + | <math>\begin{align} \frac{2z^2(2z+1)}{1-6z^2} = 2z^3 + 4z^4 + 12z^5+24z^6+72z^7+144z^8+432z^9+864z^{10}+2592z^{11}+5184z^{12}+15552z^{13}+\mathcal{O}(z^{14}) | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |||
| + | |||
| + | Der Exponent beschreibt dabei stets die Windungszahl der Krawatte, also wie oft wir sie gewickelt haben und der Vorfaktor die jeweils möglichen Umschlingungen. Da wir uns, wie weiter oben erwähnt, auf Knoten mit 13 Umschlingungen beschränken, können wir die Potenzreihe bei einem Exponenten von 13 abschneiden. | ||
| + | Nun lässt sich für einen jeden Krawattenknoten eine solche Erzeugende Funktion finden, wobei wir durch zuvor gesetzte Parameter festlegen können, wie die Sequenz von Umschlingungen endet. Für 13 Windungen erhalten wir die folgenden Möglichkeiten: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |+ | ||
| + | !Windungszahl | ||
| + | !3 | ||
| + | !4 | ||
| + | !5 | ||
| + | !6 | ||
| + | !7 | ||
| + | !8 | ||
| + | !9 | ||
| + | !10 | ||
| + | !11 | ||
| + | !12 | ||
| + | !13 | ||
| + | !total | ||
| + | |- | ||
| + | !#right windings | ||
| + | |1 | ||
| + | |1 | ||
| + | |3 | ||
| + | |5 | ||
| + | |11 | ||
| + | |21 | ||
| + | |43 | ||
| + | |85 | ||
| + | |171 | ||
| + | |341 | ||
| + | |683 | ||
| + | |1365 | ||
| + | |- | ||
| + | !#left windings | ||
| + | |0 | ||
| + | |2 | ||
| + | |2 | ||
| + | |6 | ||
| + | |10 | ||
| + | |22 | ||
| + | |42 | ||
| + | |86 | ||
| + | |170 | ||
| + | |342 | ||
| + | |682 | ||
| + | |1364 | ||
| + | |- | ||
| + | !#center windings | ||
| + | |1 | ||
| + | |1 | ||
| + | |3 | ||
| + | |5 | ||
| + | |11 | ||
| + | |21 | ||
| + | |43 | ||
| + | |85 | ||
| + | |171 | ||
| + | |341 | ||
| + | |683 | ||
| + | |1365 | ||
| + | |- | ||
| + | !#left knots | ||
| + | |0 | ||
| + | |2 | ||
| + | |4 | ||
| + | |8 | ||
| + | |24 | ||
| + | |48 | ||
| + | |144 | ||
| + | |288 | ||
| + | |864 | ||
| + | |1728 | ||
| + | |5184 | ||
| + | |8294 | ||
| + | |- | ||
| + | !#right knots | ||
| + | |1 | ||
| + | |1 | ||
| + | |4 | ||
| + | |8 | ||
| + | |24 | ||
| + | |48 | ||
| + | |144 | ||
| + | |288 | ||
| + | |864 | ||
| + | |1728 | ||
| + | |5184 | ||
| + | |8294 | ||
| + | |- | ||
| + | !#center knots | ||
| + | |1 | ||
| + | |1 | ||
| + | |4 | ||
| + | |8 | ||
| + | |24 | ||
| + | |48 | ||
| + | |144 | ||
| + | |288 | ||
| + | |864 | ||
| + | |1728 | ||
| + | |5184 | ||
| + | |8294 | ||
| + | |- | ||
| + | !#single tuck knots | ||
| + | |2 | ||
| + | |4 | ||
| + | |12 | ||
| + | |24 | ||
| + | |72 | ||
| + | |144 | ||
| + | |432 | ||
| + | |864 | ||
| + | |2592 | ||
| + | |4146 | ||
| + | |15552 | ||
| + | |84882 | ||
| + | |- | ||
| + | !total #knots | ||
| + | |2 | ||
| + | |4 | ||
| + | |20 | ||
| + | |40 | ||
| + | |192 | ||
| + | |384 | ||
| + | |1896 | ||
| + | |3792 | ||
| + | |19320 | ||
| + | |38640 | ||
| + | |202329 | ||
| + | |2666682 | ||
| + | |} | ||
| + | |||
| + | In dieser Zählung sind allerdings noch solche Krawattenknoten erlaubt, bei denen der die Krawatte falsch herum durchgezogen wurde und deshalb nicht ganz korrekterweise ein Krawattenknoten ist. Ziehen wir diesen Fehler ab, so erhalten wir eine maximale Anzahl möglichen Krawattenknoten mit 13 Bewegungen von 177146 Knoten. | ||
== Schuhe binden == | == Schuhe binden == | ||
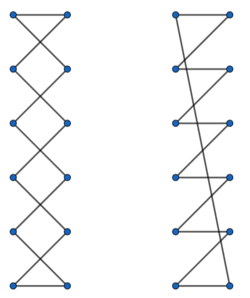
[[Datei:ZigZag and Straight.png|mini|298x298px|Überkreuz- und Sägezahnschnürung]] | [[Datei:ZigZag and Straight.png|mini|298x298px|Überkreuz- und Sägezahnschnürung]] | ||
| − | Was ist | + | Was ist die effizienteste Methode, seine Schuhe zu binden, sodass man mit einem möglichst kurzen Schnürsenkel auskommt?<ref>https://www.nature.com/articles/420476a</ref> Ist es die klassische Überkreuzschnürung? |
| − | Wir gehen von einem idealen Schuh aus, welcher <math> 2n </math> | + | Wir gehen von einem idealen Schuh aus, welcher <math> 2n </math> <math>(n\in \mathbb{N})</math> Ösen besitzt, <math>n</math> auf jeder Seite, um die Schnürsenkel zu binden. Um den Schnürsenkel mathematisch beschreiben zu können, muss er geschlossen sein. In der realen Welt ließe sich dies durch das Binden einer Schleife realisieren. Unsere Schnürung besteht aus <math>2n</math> Segmenten, wobei ein Segment jeweils die Verbindung zwischen zwei Ösen ist. Das heißt demzufolge auch, dass jede Öse nur einmal verwendet wird. Als weitere Anforderung verlangen wir, dass mindestens eines der beiden einlaufenden Schnürsenkelsegmente je Öse seinen Ursprung in der anderen Reihe der Ösen besitzt. Damit wollen wir sicherstellen, dass die zwei Seiten des Schuhs wirklich festgezogen werden. |
| − | Besitzt der Schuh auf jeder Seite gerade <math> n=1</math> Löcher, so gibt es genau eine Möglichkeit, seinen Schuh zu binden. Betrachten wir also nun einen Schuh mit <math> n\geq2</math> Löchern auf jeder Seite. Die Anzahl der möglichen Schnürungen bei <math> n</math> Löchern ergibt sich zu | + | Besitzt der Schuh auf jeder Seite gerade <math> n=1</math> Löcher, so gibt es genau eine Möglichkeit, seinen Schuh zu binden. Betrachten wir also nun einen Schuh mit <math> n\geq2</math> Löchern auf jeder Seite. Die Anzahl der möglichen Schnürungen bei <math> n</math> Löchern ergibt sich nach einer komplizierten Rechnung<ref>https://www.fieggen.com/shoelace/2trillionmethods.htm</ref> zu |
<math>\#(n)= \frac{(n!)^2}{2} \sum\limits_{k=0}^{m}\frac{1}{n-k}\binom{n-k}{k}^2 </math> | <math>\#(n)= \frac{(n!)^2}{2} \sum\limits_{k=0}^{m}\frac{1}{n-k}\binom{n-k}{k}^2 </math> | ||
mit <math> m=n/2</math> für gerade <math>n</math> und <math>m=(n-1)/2</math> für ungerade <math>n</math>. | mit <math> m=n/2</math> für gerade <math>n</math> und <math>m=(n-1)/2</math> für ungerade <math>n</math>. | ||
| + | |||
| + | Die Länge einer Schnürung ist die Summe aus allen einzelnen Teilsegmenten. Unter Verwendung von Symmetrien und Vereinfachungen ergibt sich folgendes Muster für die kürzeste Schnürung unter unseren Vorraussetzungen, wobei hier allerdings noch zwischen <math>n</math> gerade oder ungerade unterschieden werden muss. | ||
[[Datei:Shortest.png|zentriert|mini|250x250px|Unter unseren Voraussetzungen kürzeste Schnürung, links für <math> n</math> gerade, rechts zwei Beispiele für <math> n</math> ungerade]] | [[Datei:Shortest.png|zentriert|mini|250x250px|Unter unseren Voraussetzungen kürzeste Schnürung, links für <math> n</math> gerade, rechts zwei Beispiele für <math> n</math> ungerade]] | ||
| − | |||
| − | Diese Schnürung ist allerdings nicht die stärkste. Der Schnürsenkel funktioniert wie ein Flaschenzug, wenn er die zwei Reihen zusammenzieht. Allerdings hängt die Stärke der Schnürung vom Verhältnis der Abstände zwischen den einzelnen Ösen und den beiden Reihen ab. Es lässt sich ein kritisches Verhältnis <math>x_n</math> finden, sodass für <math>x\leq x_n</math>die Überkreuzbindung die stärkste Verbindung ist und für <math> x\geq x_n </math>die Sägezahnbindung die stärkste Verbindung ist. Für reale Schuhe hingegen ist dieses Verhältnis meistens in der Nähe von <math> x_n</math>, sodass die Art der Bindung keine entscheidende Rolle spielt. | + | Diese Schnürung ist allerdings nicht die stärkste. Der Schnürsenkel funktioniert wie ein Flaschenzug, wenn er die zwei Reihen zusammenzieht. Allerdings hängt die Stärke der Schnürung vom Verhältnis der Abstände zwischen den einzelnen Ösen und den beiden Reihen ab. Es lässt sich ein kritisches Verhältnis <math>x_n</math> finden, sodass für <math>x\leq x_n</math>die Überkreuzbindung die stärkste Verbindung ist und für <math> x\geq x_n </math>die Sägezahnbindung die stärkste Verbindung ist (siehe Bild rechts oben). Für reale Schuhe hingegen ist dieses Verhältnis meistens in der Nähe von <math> x_n</math>, sodass die Art der Bindung keine entscheidende Rolle spielt. |
== Zwei Nägel und ein Bild == | == Zwei Nägel und ein Bild == | ||
| − | |||
| − | + | [[Datei:Zweinagelproblem.jpg|mini|Lösung des Zweinagelproblems]] | |
| + | [[Datei:Zweinagelproblem lsg1.jpg|mini|Systematische graphische Darstellung der gleichen Lösung]] | ||
| + | Meist werden Bilder bekanntermaßen ganz simpel und ohne mathematische Rafinesse mit einem oder zwei Nägeln an der Wand befestigt. Möchte man jedoch eine Weise finden, bei einer Aufhängung mit 2 Nägeln das Bild nur durch die Entfernung eines der beiden Nägel abhängen zu können (etwa um an den dahinterliegenden Tresor zu gelangen), so braucht es hierfür eine geschicktere Konstruktion. | ||
| − | + | Eine mächtige Methode, einen geeigneten Knoten zu finden, funktioniert auf die folgende Art und Weise <ref>https://arxiv.org/pdf/1203.3602.pdf</ref>: Man definiert für die Notation zunächst die Symbole <math>x_1,{x_1}^{-1},...,x_n, {x_n}^{-1}</math>, während hierbei jeweils <math>x_i</math> die Umschlingung des <math>i</math>-ten Nagels im Urzeigersinn und <math>{x_i}^{-1}</math> jene gegen den Uhrzeigersinn beschreibt. Eine Umschlingung meint hierbei eine vollständige Umrundung des Nagels, wobei der Faden von unten kommt und auch wieder nach unten abgeführt wird. und außerdem von der linken Bildecke kommend so gelegt wird, dass bei Kreuzungen die zuvor gelegten Teile des Fadens immer überkreuzt werden. Somit lässt sich schließlich aus der Notation eindeutig der zugehörige Knoten konstruieren. Zur Verdeutlichung ist für die Lösung des Zweinagelproblems unter der äquivalenten, aber übersichtlicheren Darstellung des Knotens eine weitere Abbildung zu sehen, in welcher der Bezug zur Notation und deren Eindeutigkeit klarer erkennbar ist. Wendet man diese Notation auf das oben beschriebene Problem mit zwei Nägeln an, so kann man sich leicht davon überzeugen, dass | |
| − | + | <math>S_2:=x_1x_2{x_1}^{-1}{x_2}^{-1}</math> | |
| + | eine Lösung ist, die die Voraussetzungen erfüllt. Denn sobald man nun einen Nagel hinauszieht, werden die darauf bezogenen Umschlingungen obsolet und es bleibt eine Umschlingung um den anderen Nagel im und eine gegen den Uhrzeigersinn übrig, wodurch das Bild auch diese scheinbare Aufhängung verliert und hinabfällt. Für die späteren Überlegungen lohnt es sich, dies als Kommutator <math>[x_1,x_2]=x_1x_2{x_1}^{-1}{x_2}^{-1}</math> einzuführen. | ||
| − | + | ===n-Nagel-Problem=== | |
| + | [[Datei:Dreinagelproblem.jpg|mini|Eine Lösung des Dreinagelproblems]] | ||
| + | Nun lässt sich diese Erkenntnis auch auf das Problem erweitern, ein Bild mit n Nägeln aufhängen zu wollen, welches erneut durch das Ziehen eines beliebigen Nagels abgehängt werden kann. Für das 3-Nagel-Problem wäre etwa eine Lösung, die bekannte 2-Nagel-Lösung <math>S_2</math> zu nutzen und durch | ||
| − | == | + | <math>[S_2,x_3]=S_2x_3{S_2}^{-1}{x_3}^{-1}=x_1x_2{x_1}^{-1}{x_2}^{-1}x_3x_2x_1{x_2}^{-1}{x_1}^{-1}{x_3}^{-1}</math> |
| − | ===Trivia | + | zu variieren. Der entsprechende Knoten ist rechts skizziert. (Dies löst offensichtlich unser Problem, da bei Ziehung des ersten oder zweiten Nagels sowohl <math>S_2</math> als auch dessen Inverses hinfällig wird und auch bei Ziehung des dritten Nagels nur noch eine Folge von Umschlingungen und ihr Inverses übrigbleiben, also das Bild ebenfalls hinabfällt.) |
| + | |||
| + | Analog ergibt sich für 4 Nägel erneut induktiv die folgende Lösung: | ||
| + | |||
| + | <math>[S_3,x_4]=S_3x_4{S_3}^{-1}{x_4}^{-1}=...=x_1x_2{x_1}^{-1}{x_2}^{-1}x_3x_2x_1{x_2}^{-1}{x_1}^{-1}{x_3}^{-1}x_4x_3x_1x_2{x_1}^{-1}{x_2}^{-1}{x_3}^{-1}x_2x_1{x_2}^{-1}{x_1}^{-1}</math> | ||
| + | |||
| + | Der bedeutende Nachteil dieser Methode ist ihre Ineffizienz: Man benötigt <math>2^n+2^{n-1}-2</math> Umschlingungen. Der Beweis durch vollständige Induktion ist hier ausgeführt: | ||
| + | <br>'''IA:''' Der behandelte Fall des 2-Nagel-Problems besitzt <math>2^2+2^1-2=4</math> Umschlingungen. | ||
| + | <br>'''IV:''' Die Aussage gelte für <math>n\in \lbrace2, i-1\rbrace</math> | ||
| + | <br>'''IS:''' Bezeichne <math>\# (S_i)</math> die Anzahl der Umschlingungen bei der Lösung des i-Nagel-Problems. Wegen <math>S_i=[S_{i-1},x_i]</math> gilt dann mit der IV: <math>\#(S_i)=2\cdot\#(S_{i-1})+2=2\cdot(2^{i-1}+2^{i-2}-2)+2=2^i+2^{i-1}-2</math> | ||
| + | |||
| + | Es sei hier angemerkt, dass man auch effizientere Konstruktionen der Knoten finden kann. So braucht etwa das 4-Nagelproblem auf die beschriebene Weise <math>\#(S_4)=22</math> Umschlingungen. <math>[S_2,S_2]</math> ist jedoch auch eine Lösung und benötigt lediglich <math>4\cdot\#(S_2)=16</math> Umschlingungen. | ||
| + | |||
| + | Ferner kann man sich auch überlegen, wie man ein Bild mit [math]n[/math] Nägeln so aufhängt, dass es genau dann herabfällt, wenn davon <math>k</math> herausgezogen werden. Dies sei an dieser Stelle unter Verweis auf die verwendete Quelle jedoch dem/der Leser:in überlassen. | ||
| + | |||
| + | ==Trivia== | ||
Wenn Ihnen dieser Artikel gefallen hat, könnte Ihnen auch das [[Museumswächterproblem]] gefallen. ^^ | Wenn Ihnen dieser Artikel gefallen hat, könnte Ihnen auch das [[Museumswächterproblem]] gefallen. ^^ | ||
| − | == Quellen == | + | |
| + | == Autoren == | ||
| + | Daniela Müller-Trefzer, Hjalmar Brunßen, Lasse Bassermann, Joris Hoffmann | ||
| + | |||
| + | ==Quellen== | ||
<references /> | <references /> | ||
Aktuelle Version vom 11. Oktober 2021, 09:49 Uhr
In diesem Artikel geht es darum, wie man mehr oder weniger alltägliche Probleme mithilfe der Kontentheorie beschreiben und sogar lösen kann. Wie nützlich die hier gezeigten Lösungen zu Problemen vom Schuhe schnüren über das Krawatte binden bis hin zum Bilder aufhängen ist, mag der geneigte Leser selbst entscheiden.
Grundlagen[1]
Ein Knoten ist mathematisch eine Einbettung des Kreises [math]S^1[/math] in den dreidimensionalen euklidischen Raum [math]\mathbb{R}^3[/math].
Wir betrachten im Folgenden nur die reguläre Projektion eines Knotens in den zweidimensionalen Raum [math]\mathbb{R}^2[/math]. Reguläre Projektionen sind solche, welche überall bis auf die Punkte der Kreuzungen injektiv sind und eine endliche Anzahl dieser Kreuzungspunkte besitzen. Zudem fordern wir, dass die Punkte an einer Kreuzung nicht kolinear sein dürfen, dass bedeutet ein Kreuzungspunkt ist kein Berührpunkt.
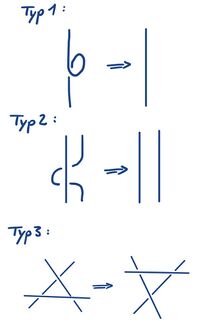
Die Projektion des Knotens ist nicht eindeutig. Zwei Projektionen gehören genau dann zum gleichen Knoten, wenn sie mithilfe einer Hintereinanderausführung von sogenannten Reidemeisterbewegungen ineinander überführt werden können. Dabei ist es erlaubt eine Schlaufe zu bilden oder zu lösen (Bewegunstyp 1), sich überlappende Stränge in in parallel verlaufende umzuwandeln (Bewegungstyp 2) und den Strang über einer darunter liegenden Kreuzung zu verschieben (Bewegungstyp 3).
Keltische Knoten und deren Darstellungen
Ein keltischer Knoten ist ebenfalls eine wie schon zuvor definierte reguläre Projektion eines Knotens mit der zusätzlichen Einschränkung, dass sich für jeden Strang Über- und Unterkreuzungen stets abwechseln müssen.[2]
Die reguläre Projektion eines Knotens ist graphentheoretisch ein sogenannter medialer Graph, zu dem wiederum ein planerer Graph gehört. [3] Ein planerer Graph ist ein Paar [math]G=(V,E)[/math], mit der endlichen Menge der Vertices [math]V\neq\emptyset[/math] und der ebenfalls endlichen Menge der Kanten [math]E\subseteq\lbrace\lbrace u,v\rbrace\lvert u,v\in V, u\neq v\rbrace[/math].
Die Darstellung des Knotens als planarer Graph, erhalten wir mithilfe der folgenden Schritte:
Wir betrachten zu Beginn den medialen Graphen und färben diesen zunächst schachbrettartig ein, indem wir die Fläche außerhalb des Graphen weiß färben und anschließend alle anderen durch die Kanten des Graphen abgegrenzten Flächen so färben, dass jede Kante eine weiße von einer schwarz gefärbten Fläche abtrennt.
Anschließend definieren wir in jeder schwarz gefärbte Fläche einen Vertex des planaren Graphen und verbinden diese über die Kreuzungen des medialen Graphen mit den angrenzenden Vertices.
Damit die Information erhalten bleibt, wie sich die Stränge an den Kreuzungspunkten über- oder unterkreuzen, kennzeichnen wir die Kanten auf zwei unterschiedliche Weisen:
Falls die Fläche links neben dem überkreuzenden Strang schwarz ist kennzeichnen wir dies mit einer durchgezogenen Kante. Dabei ist es wichtig dem Verlauf des Strangs in Richtung der Kreuzung zu folgen.
Falls hingegen die schwarze Fläche rechts neben dem obenliegenden Strang liegt, so wird die neue Kante des planaren Graphen gestrichelt.[4]
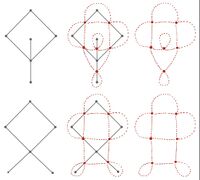
Umgekehrt existiert auch der inverse Prozess und es kann aus einem solchen planaren Graph der zugehörige mediale konstruiert werden (Allerdings sei angemerkt, dass zueinander isomorphe planare Graphen nicht zwingend zueinander isomorphe mediale Graphen besitzen).
Hierfür zeichnen wir in die Mitte jeder Kante ein Kreuz, welches anschließend einen Vertex definiert. Für jede Fläche im planaren Graphen (dazu gehört etwa auch die Fläche außerhalb des Graphen) werden benachbarte Kreuze bzw. neue Vertices, also solche zwischen denen im planaren Graph nur eine Ecke ist, miteinander verbunden. Insbesondere werden Ecken auch innerhalb einer Fläche doppelt verbunden, wenn sie zweifach benachbart sind. Entsprechend der Art der Kante (durchgezogen/gestrichelt) und nach Schachbrettmusterung wie im vorigen Abschnitt beschrieben ist an den Kreuzungspunkten festgelegt, welcher Strang über- und welcher unterkreuzt.
Auf diese Art lassen sich sehr einfach keltische Knoten konstruieren. Es sei angemerkt, dass die Eigenschaft des abwechselnden Über- und Unterkreuzens dann gewährleistet ist, wenn der planare Graph entweder nur aus durchgezogenen (linkskreuzenden) oder nur aus gestrichelten (rechtskreuzenden) Kanten besteht.
[5]Die Mathematik des Krawattenbindens
Krawatten sind seit Ludwig dem XIV als modisches Accesoire bekannt und seither müssen sich die Träger um einen Knoten bemühen, um ihre Krawatte zu befestigen. Auswahl gibt es genug, den einfachen Four-in-Hand, den (halben) Windsorknoten, den Cavendish-Knoten, den kleinen Knoten und viele mehr. Die meisten dürften nicht sehr viele verschiedene Arten der Krawattenbefestigung kennen, dabei existieren 85 mögliche Knoten zum Binden einer Krawatte mit 8 Zügen, die allerdings nicht alle Balance, Symmetrie und Form berücksichtigen, wie der theoretische Physiker Thomas Fink und die Mathematikerin Yong Mao herausfanden [6]. Aus praktischen Gründen werden also nicht alle davon realisiert, zum Einen sind unendlich lange Krawatten leider noch nicht erfunden, zum Anderen müsste man dann eventuell einen sehr schweren, unförmigen Krawattenknoten um den Hals tragen und bekäme davon bestimmt Rückenschmerzen. Dieser Gedanke lässt sich auch noch weiterführen. Wir wollen uns fragen, wie viele Möglichkeiten es gibt, eine Krawatte mit 13 Zügen zu binden, denn gerade schmale Krawatten werden häufiger umeinandergeschlungen und -gewickelt als breite [7]. Diese Anzahl ergibt sich daraus, dass breite Krawatten gewöhnlicherweise 9 Mal binden lassen, während schmale maximal 15 Mal umeinander gewickelt werden. Um den Komfort zu erhalten, nehmen wir eine etwas kleinere Zahl als möglich an.
Zunächst führen wir eine Sprache ein, um eine Krawatte und ihren Knoten allgemein beschreiben zu können. Wir führen ein, dass wir immer ein aktives schmales Ende der Krawatte haben und das andere, breite Ende festhalten, damit es nicht verrutscht. Weiterhin teilen wir den Krawattenbinder in drei Regionen ein, die durch seine Krawatte eingeteilt werden, einen linken, einen rechten und einen zentralen Teil und bezeichnen sie mit [math] L [/math], [math] C [/math] und [math]R[/math] (left, center, right). Wir schreiben [math]\odot[/math], wenn wir die den schmalen Teil der Krawatte "aus der Ebene hinaus" ziehen und [math]\otimes [/math], wenn wir den schmalen Teil der Krawatte "in die Ebene hinein" ziehen. Außerdem schreiben wir [math]U[/math] dafür, wenn wir die schmale Seite der Krawatte durch eine zuvor entstandene Schlaufe ziehen, wie es am Ende eines jeden Krawattenknotens der Fall ist. Dies ist offensichtlich nur dann erlaubt, wenn wir die Krawatte im letzten Zug "aus der Ebene heraus" gezogen wurde. Mit großen Symbolen beschreiben wir also jeweils die Lage des breiten Endes der Krawatte, wenn das schmale Ende sich um das Zentrum [math]C[/math] schlingt, mit dem Index die Richtung, in der wir die Krawatte ziehen und [math]U[/math] beschreibt eine Umwicklung, wie oben beschrieben. Somit erhalten wir die folgenden möglichen Bewegungen, die wir mit der Krawatte durchführen können: [math]\{L_{\otimes}, L_{\odot}, C_{\otimes}, C_{\odot}, R_{\otimes}, R_{\odot}, U\}[/math] Um die Stabilität der Krawatte zu gewährleisten führen wir einige Regeln ein:
- [math](L,C,R)[/math] darf sich nicht wiederholen, d.h. gleiche Symbole dürfen nicht aufeinander folgen. [math]U[/math] ist davon unabhängig und auch eine Folge aus [math](LCR)U(LCR)[/math] ist nicht erlaubt.
- [math]\otimes[/math] und [math]\odot[/math] dürfen sich nicht direkt wiederholen. [math]U[/math] ist unabhängig davon.
- [math]U[/math] darf nur direkt auf eine Bewegung nach außen folgen.
- Ein Knoten darf nur mit [math]C_{\otimes}, C_{\odot}, U[/math] enden.
- Eine [math]k[/math]-fache Umschlingung ist erst erlaubt, wenn zuvor [math]2k[/math] andere Bewegungen ausgeführt wurden.
Wir können im Folgenden die Symbole [math]\otimes[/math] und [math]\odot[/math] direkt weglassen, da sich stets aus dem letzten rekonstruieren lässt, mit welcher Bewegung wir begonnen haben (die letzte Bewegung muss nach außen gehen, da wir den Knoten mit [math]U[/math] beendet werden muss und Regel 3 erfüllt ist und außen und innen müssen sich stets abwechseln). Weiterhin können wir die Krawatte entweder im ([math]T[/math]) oder gegen den Uhrzeigersinn ([math]W[/math]) umschlingen, denn [math] RUR [/math], [math] CUC [/math] und [math] LUL [/math] können nicht auftreten wegen unserer ersten Annahme. Die Position des aktiven (schmalen) Teils der Krawatte lässt sich dann beschreiben als [math]\#W-\#T (mod 3)[/math]. Elementare Überlegungen führen uns auf die Tatsache, dass wenn wir den Krawattenknoten mit [math]W[/math] begonnen haben gelten muss [math]\#W-\#T = 2 (mod 3)[/math] und wenn wir den Knoten mit [math]T[/math] begonnen haben gelten muss [math]\#T-\#W = 2 (mod 3)[/math] für eine k-fache Umwicklung einer 2k-langen Sequenz. Hierbei fließt mit ein, dass die erste Bewegung die Schlaufe bildet, durch die das schmale Krawattenende zum Schluss gezogen wird. Gewöhnlicherweise muss die Krawatte von der Seite kommen, von der die Schlaufe kommt. Jede andere Schlaufe von links nach rechts oder rechts nach links muss vor oder hinter dem Knoten liegen und zwischen dem ersten und dem vorletzten liegen [math]2k-1[/math] Umschlingungen. In diesen muss die Krawatte die Krawatte auf die richtige Seite gebracht werden und daraus folgt die oben aufgestellte Behauptung.
Nun wollen wir eine Grammatik aufbauen, die beschreibt, wie wir die Krawatte binden können. Hierfür verwenden wir die Backus-Naur-Form [8]. Es handelt sich hierbei um eine kontextfreie Grammatik, die in der Informatik Anwendung findet. Dabei werden neue Symbole definiert, indem bereits bekannte Symbole durch Leer-, Zeilen- und Spaltentrennzeichen definiert werden. Hierdurch können Umschlingungsfolgen zusammengefasst werden.
Nun können wir für unseren Krawattenknoten unter Verwendung der oben erwähnten Grammatik Erzeugende Funktionen [9] finden, die sich durch eine formale Potenzreihe [math] \begin{align}f(z) = \sum\limits_{n=0}^{\infty} a_nz^n \end{align}[/math] darstellen lassen. Mittels eines Computers und der zuvor definierten Grammatik lässt sich eine solche Erzeugenden Funktion finden. So wird ein einfacher Krawattenknoten beschrieben durch [math]\begin{align} \frac{2z^2(2z+1)}{1-6z^2} = 2z^3 + 4z^4 + 12z^5+24z^6+72z^7+144z^8+432z^9+864z^{10}+2592z^{11}+5184z^{12}+15552z^{13}+\mathcal{O}(z^{14}) \end{align} [/math]
Der Exponent beschreibt dabei stets die Windungszahl der Krawatte, also wie oft wir sie gewickelt haben und der Vorfaktor die jeweils möglichen Umschlingungen. Da wir uns, wie weiter oben erwähnt, auf Knoten mit 13 Umschlingungen beschränken, können wir die Potenzreihe bei einem Exponenten von 13 abschneiden.
Nun lässt sich für einen jeden Krawattenknoten eine solche Erzeugende Funktion finden, wobei wir durch zuvor gesetzte Parameter festlegen können, wie die Sequenz von Umschlingungen endet. Für 13 Windungen erhalten wir die folgenden Möglichkeiten:
| Windungszahl | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | total |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| #right windings | 1 | 1 | 3 | 5 | 11 | 21 | 43 | 85 | 171 | 341 | 683 | 1365 |
| #left windings | 0 | 2 | 2 | 6 | 10 | 22 | 42 | 86 | 170 | 342 | 682 | 1364 |
| #center windings | 1 | 1 | 3 | 5 | 11 | 21 | 43 | 85 | 171 | 341 | 683 | 1365 |
| #left knots | 0 | 2 | 4 | 8 | 24 | 48 | 144 | 288 | 864 | 1728 | 5184 | 8294 |
| #right knots | 1 | 1 | 4 | 8 | 24 | 48 | 144 | 288 | 864 | 1728 | 5184 | 8294 |
| #center knots | 1 | 1 | 4 | 8 | 24 | 48 | 144 | 288 | 864 | 1728 | 5184 | 8294 |
| #single tuck knots | 2 | 4 | 12 | 24 | 72 | 144 | 432 | 864 | 2592 | 4146 | 15552 | 84882 |
| total #knots | 2 | 4 | 20 | 40 | 192 | 384 | 1896 | 3792 | 19320 | 38640 | 202329 | 2666682 |
In dieser Zählung sind allerdings noch solche Krawattenknoten erlaubt, bei denen der die Krawatte falsch herum durchgezogen wurde und deshalb nicht ganz korrekterweise ein Krawattenknoten ist. Ziehen wir diesen Fehler ab, so erhalten wir eine maximale Anzahl möglichen Krawattenknoten mit 13 Bewegungen von 177146 Knoten.
Schuhe binden
Was ist die effizienteste Methode, seine Schuhe zu binden, sodass man mit einem möglichst kurzen Schnürsenkel auskommt?[10] Ist es die klassische Überkreuzschnürung?
Wir gehen von einem idealen Schuh aus, welcher [math] 2n [/math] [math](n\in \mathbb{N})[/math] Ösen besitzt, [math]n[/math] auf jeder Seite, um die Schnürsenkel zu binden. Um den Schnürsenkel mathematisch beschreiben zu können, muss er geschlossen sein. In der realen Welt ließe sich dies durch das Binden einer Schleife realisieren. Unsere Schnürung besteht aus [math]2n[/math] Segmenten, wobei ein Segment jeweils die Verbindung zwischen zwei Ösen ist. Das heißt demzufolge auch, dass jede Öse nur einmal verwendet wird. Als weitere Anforderung verlangen wir, dass mindestens eines der beiden einlaufenden Schnürsenkelsegmente je Öse seinen Ursprung in der anderen Reihe der Ösen besitzt. Damit wollen wir sicherstellen, dass die zwei Seiten des Schuhs wirklich festgezogen werden.
Besitzt der Schuh auf jeder Seite gerade [math] n=1[/math] Löcher, so gibt es genau eine Möglichkeit, seinen Schuh zu binden. Betrachten wir also nun einen Schuh mit [math] n\geq2[/math] Löchern auf jeder Seite. Die Anzahl der möglichen Schnürungen bei [math] n[/math] Löchern ergibt sich nach einer komplizierten Rechnung[11] zu
[math]\#(n)= \frac{(n!)^2}{2} \sum\limits_{k=0}^{m}\frac{1}{n-k}\binom{n-k}{k}^2 [/math]
mit [math] m=n/2[/math] für gerade [math]n[/math] und [math]m=(n-1)/2[/math] für ungerade [math]n[/math].
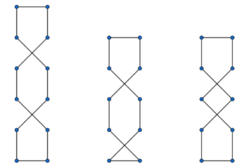
Die Länge einer Schnürung ist die Summe aus allen einzelnen Teilsegmenten. Unter Verwendung von Symmetrien und Vereinfachungen ergibt sich folgendes Muster für die kürzeste Schnürung unter unseren Vorraussetzungen, wobei hier allerdings noch zwischen [math]n[/math] gerade oder ungerade unterschieden werden muss.
Diese Schnürung ist allerdings nicht die stärkste. Der Schnürsenkel funktioniert wie ein Flaschenzug, wenn er die zwei Reihen zusammenzieht. Allerdings hängt die Stärke der Schnürung vom Verhältnis der Abstände zwischen den einzelnen Ösen und den beiden Reihen ab. Es lässt sich ein kritisches Verhältnis [math]x_n[/math] finden, sodass für [math]x\leq x_n[/math]die Überkreuzbindung die stärkste Verbindung ist und für [math] x\geq x_n [/math]die Sägezahnbindung die stärkste Verbindung ist (siehe Bild rechts oben). Für reale Schuhe hingegen ist dieses Verhältnis meistens in der Nähe von [math] x_n[/math], sodass die Art der Bindung keine entscheidende Rolle spielt.
Zwei Nägel und ein Bild
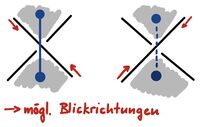
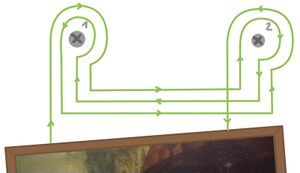
Meist werden Bilder bekanntermaßen ganz simpel und ohne mathematische Rafinesse mit einem oder zwei Nägeln an der Wand befestigt. Möchte man jedoch eine Weise finden, bei einer Aufhängung mit 2 Nägeln das Bild nur durch die Entfernung eines der beiden Nägel abhängen zu können (etwa um an den dahinterliegenden Tresor zu gelangen), so braucht es hierfür eine geschicktere Konstruktion.
Eine mächtige Methode, einen geeigneten Knoten zu finden, funktioniert auf die folgende Art und Weise [12]: Man definiert für die Notation zunächst die Symbole [math]x_1,{x_1}^{-1},...,x_n, {x_n}^{-1}[/math], während hierbei jeweils [math]x_i[/math] die Umschlingung des [math]i[/math]-ten Nagels im Urzeigersinn und [math]{x_i}^{-1}[/math] jene gegen den Uhrzeigersinn beschreibt. Eine Umschlingung meint hierbei eine vollständige Umrundung des Nagels, wobei der Faden von unten kommt und auch wieder nach unten abgeführt wird. und außerdem von der linken Bildecke kommend so gelegt wird, dass bei Kreuzungen die zuvor gelegten Teile des Fadens immer überkreuzt werden. Somit lässt sich schließlich aus der Notation eindeutig der zugehörige Knoten konstruieren. Zur Verdeutlichung ist für die Lösung des Zweinagelproblems unter der äquivalenten, aber übersichtlicheren Darstellung des Knotens eine weitere Abbildung zu sehen, in welcher der Bezug zur Notation und deren Eindeutigkeit klarer erkennbar ist. Wendet man diese Notation auf das oben beschriebene Problem mit zwei Nägeln an, so kann man sich leicht davon überzeugen, dass
[math]S_2:=x_1x_2{x_1}^{-1}{x_2}^{-1}[/math]
eine Lösung ist, die die Voraussetzungen erfüllt. Denn sobald man nun einen Nagel hinauszieht, werden die darauf bezogenen Umschlingungen obsolet und es bleibt eine Umschlingung um den anderen Nagel im und eine gegen den Uhrzeigersinn übrig, wodurch das Bild auch diese scheinbare Aufhängung verliert und hinabfällt. Für die späteren Überlegungen lohnt es sich, dies als Kommutator [math][x_1,x_2]=x_1x_2{x_1}^{-1}{x_2}^{-1}[/math] einzuführen.
n-Nagel-Problem
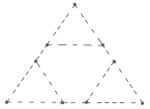
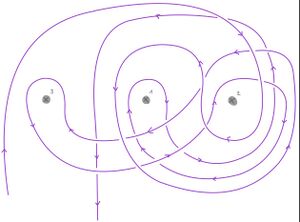
Nun lässt sich diese Erkenntnis auch auf das Problem erweitern, ein Bild mit n Nägeln aufhängen zu wollen, welches erneut durch das Ziehen eines beliebigen Nagels abgehängt werden kann. Für das 3-Nagel-Problem wäre etwa eine Lösung, die bekannte 2-Nagel-Lösung [math]S_2[/math] zu nutzen und durch
[math][S_2,x_3]=S_2x_3{S_2}^{-1}{x_3}^{-1}=x_1x_2{x_1}^{-1}{x_2}^{-1}x_3x_2x_1{x_2}^{-1}{x_1}^{-1}{x_3}^{-1}[/math]
zu variieren. Der entsprechende Knoten ist rechts skizziert. (Dies löst offensichtlich unser Problem, da bei Ziehung des ersten oder zweiten Nagels sowohl [math]S_2[/math] als auch dessen Inverses hinfällig wird und auch bei Ziehung des dritten Nagels nur noch eine Folge von Umschlingungen und ihr Inverses übrigbleiben, also das Bild ebenfalls hinabfällt.)
Analog ergibt sich für 4 Nägel erneut induktiv die folgende Lösung:
[math][S_3,x_4]=S_3x_4{S_3}^{-1}{x_4}^{-1}=...=x_1x_2{x_1}^{-1}{x_2}^{-1}x_3x_2x_1{x_2}^{-1}{x_1}^{-1}{x_3}^{-1}x_4x_3x_1x_2{x_1}^{-1}{x_2}^{-1}{x_3}^{-1}x_2x_1{x_2}^{-1}{x_1}^{-1}[/math]
Der bedeutende Nachteil dieser Methode ist ihre Ineffizienz: Man benötigt [math]2^n+2^{n-1}-2[/math] Umschlingungen. Der Beweis durch vollständige Induktion ist hier ausgeführt:
IA: Der behandelte Fall des 2-Nagel-Problems besitzt [math]2^2+2^1-2=4[/math] Umschlingungen.
IV: Die Aussage gelte für [math]n\in \lbrace2, i-1\rbrace[/math]
IS: Bezeichne [math]\# (S_i)[/math] die Anzahl der Umschlingungen bei der Lösung des i-Nagel-Problems. Wegen [math]S_i=[S_{i-1},x_i][/math] gilt dann mit der IV: [math]\#(S_i)=2\cdot\#(S_{i-1})+2=2\cdot(2^{i-1}+2^{i-2}-2)+2=2^i+2^{i-1}-2[/math]
Es sei hier angemerkt, dass man auch effizientere Konstruktionen der Knoten finden kann. So braucht etwa das 4-Nagelproblem auf die beschriebene Weise [math]\#(S_4)=22[/math] Umschlingungen. [math][S_2,S_2][/math] ist jedoch auch eine Lösung und benötigt lediglich [math]4\cdot\#(S_2)=16[/math] Umschlingungen.
Ferner kann man sich auch überlegen, wie man ein Bild mit [math]n[/math] Nägeln so aufhängt, dass es genau dann herabfällt, wenn davon [math]k[/math] herausgezogen werden. Dies sei an dieser Stelle unter Verweis auf die verwendete Quelle jedoch dem/der Leser:in überlassen.
Trivia
Wenn Ihnen dieser Artikel gefallen hat, könnte Ihnen auch das Museumswächterproblem gefallen. ^^
Autoren
Daniela Müller-Trefzer, Hjalmar Brunßen, Lasse Bassermann, Joris Hoffmann
Quellen
- ↑ https://en.wikipedia.org/wiki/Knot_(mathematics)
- ↑ http://www.bilder-der-mathematik.de/picturebook/pages/picturebook_pages_100_101.pdf
- ↑ https://en.wikipedia.org/wiki/Medial_graph
- ↑ http://www.entrelacs.net/Die-Grundlagen
- ↑ http://export.arxiv.org/pdf/1401.8242
- ↑ https://en.wikipedia.org/wiki/The_85_Ways_to_Tie_a_Tie
- ↑ http://export.arxiv.org/pdf/1401.8242
- ↑ https://de.wikipedia.org/wiki/Backus-Naur-Form
- ↑ https://de.wikipedia.org/wiki/Erzeugende_Funktion
- ↑ https://www.nature.com/articles/420476a
- ↑ https://www.fieggen.com/shoelace/2trillionmethods.htm
- ↑ https://arxiv.org/pdf/1203.3602.pdf