Magische Quadrate: Unterschied zwischen den Versionen
| (51 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
==Definition== | ==Definition== | ||
[[Datei:Bild1.png|mini|102x102px]] | [[Datei:Bild1.png|mini|102x102px]] | ||
| − | Ein magisches Quadrat der Ordnung n beschreibt eine n×n Matrix, in welcher paarweise verschiedene ganze Zahlen, häufig 1,..., <math>n^2 </math>, so angeordnet sind, dass die Summe der Zeilen- und | + | Ein '''magisches Quadrat''' der Ordnung n beschreibt eine n×n Matrix, in welcher paarweise verschiedene ganze Zahlen, häufig 1,..., <math>n^2 </math>, so angeordnet sind, dass die Summe der Hautdiagonalen-, Zeilen- und Spalteneinträge dem gleichen Wert entspricht. Diesen nennt man die '''magische Summe <math> s^* </math>'''. |
| − | Man spricht von einem semimagischen Quadrat, falls die Hauptdiagonalen nicht der magischen Summe entsprechen. | + | Man spricht von einem '''semimagischen Quadrat''', falls die Hauptdiagonalen nicht der magischen Summe entsprechen. |
<br />Für die Einträge <math> 1,.., n^2 </math> entspricht die magische Summe <math> s^* = \frac{1}{n} \sum\limits_{k=1}^{n^2} k</math>. | <br />Für die Einträge <math> 1,.., n^2 </math> entspricht die magische Summe <math> s^* = \frac{1}{n} \sum\limits_{k=1}^{n^2} k</math>. | ||
| + | |||
== Magische Quadrate niedriger Ordnung == | == Magische Quadrate niedriger Ordnung == | ||
<!-- Im folgenden betrachten wir magische Quadrate mit niedriger Ordnung. Da sich durch komponentenweise Addition zweier magischer Quadrate und die Multiplikation mit einem Skalar nur die magische Summe ändert, aber die Eigenschaft des magischen Quadrats erhalten bleibt, betrachten wir im folgenden nur ??? magische Quadrate. !--> | <!-- Im folgenden betrachten wir magische Quadrate mit niedriger Ordnung. Da sich durch komponentenweise Addition zweier magischer Quadrate und die Multiplikation mit einem Skalar nur die magische Summe ändert, aber die Eigenschaft des magischen Quadrats erhalten bleibt, betrachten wir im folgenden nur ??? magische Quadrate. !--> | ||
| − | === Magische Quadrate 1 | + | === Magische Quadrate 1. Ordnung === |
Magische Quadrate erster Ordnung besitzen nur einen Eintrag und sind somit trivial, da jede 1×1-Matrix die Eigenschaft eines magischen Quadrates erfüllt. | Magische Quadrate erster Ordnung besitzen nur einen Eintrag und sind somit trivial, da jede 1×1-Matrix die Eigenschaft eines magischen Quadrates erfüllt. | ||
| − | + | Magisches Quadrat 1-ter Ordnung | |
<math> | <math> | ||
\begin{bmatrix} | \begin{bmatrix} | ||
| Zeile 16: | Zeile 17: | ||
</math> | </math> | ||
mit <math>a \in \mathbb{Z} </math> | mit <math>a \in \mathbb{Z} </math> | ||
| − | === Magische Quadrate 2 | + | === Magische Quadrate 2. Ordnung === |
| − | Nach der oben aufgeführten Definition | + | Nach der oben aufgeführten Definition existieren keine magischen Quadrate zweiter Ordnung. Vernachlässigt man die Bedingung der paarweise verschiedenen Einträge, haben magische bzw. semimagische Quadrate folgende Form: |
| − | + | Magisches Quadrat 2-ter Ordnung | |
<math> | <math> | ||
\begin{bmatrix} | \begin{bmatrix} | ||
| Zeile 28: | Zeile 29: | ||
mit <math>a \in \mathbb{Z} </math> | mit <math>a \in \mathbb{Z} </math> | ||
| − | + | Semimagisches Quadrat 2-ter Ordnung | |
<math> | <math> | ||
\begin{bmatrix} | \begin{bmatrix} | ||
| Zeile 36: | Zeile 37: | ||
</math> | </math> | ||
mit <math>a, b \in \mathbb{Z} </math> | mit <math>a, b \in \mathbb{Z} </math> | ||
| − | === Magische Quadrate 3 | + | |
| + | === Magische Quadrate 3. Ordnung === | ||
Um den Aufbau eines magischen Quadrats dritter Ordnung zu verdeutlichen betrachten wir folgende Matrix | Um den Aufbau eines magischen Quadrats dritter Ordnung zu verdeutlichen betrachten wir folgende Matrix | ||
| Zeile 51: | Zeile 53: | ||
Sei <math>s^* \in \mathbb{Z}</math> die magische Summe, so muss A folgende Eigenschaft erfüllen: | Sei <math>s^* \in \mathbb{Z}</math> die magische Summe, so muss A folgende Eigenschaft erfüllen: | ||
| − | <math>s^* - e = a + i = b + h = c + g = f + d </math> | + | '''<math>s^* - e = a + i = b + h = c + g = f + d </math>''' |
| − | Daraus lässt sich folgern, dass <math>a + b + ... + h + i = 4* (s^*-e)+e </math> gilt. Darüber hinaus gilt <math> a+b+...+h+i= 3s^*</math>, daraus folgt <math> s^* = 3e</math>. | + | |
| + | Daraus lässt sich folgern, dass <math>a + b + ... + h + i = 4* (s^*-e)+e </math> gilt. | ||
| + | |||
| + | Darüber hinaus gilt <math> a+b+...+h+i= 3s^*</math>, daraus folgt zusammen <math> s^* = 3e</math>. | ||
| − | Mit diesen | + | Mit diesen Voraussetzungen, welche durch die Definition gegeben sind, lassen sich magische Quadrate der Ordnung 3 für die Zahlen 1,...,9 leicht konstruieren. Die magische Summe ergibt sich als <math> s^* = \frac{1}{3} \sum\limits_{k=1}^{9} k = 15</math>. Somit gilt <math>e=5 </math> und <math> 10 = a + i = b + h = c + g = f + d</math>. Es gilt <math> 10 = 1+9 = 2+8 = 3 + 7= 4+6</math>. Nehmen wir nun a=1 an, so erhalten wir |
| − | <math>14 = b+c = d+g </math> und <math> 6 = f+c =h+g</math>. Da es je nur ein Paar gibt, welches gleich 14 bzw. gleich | + | <math>14 = b+c = d+g </math> und <math> 6 = f+c =h+g</math>. Da es je nur ein Paar gibt, welches gleich 14 bzw. gleich 6 ist, folgt, dass die Werte 1 und 9 nicht in einer der Ecken liegen können. Des Weiteren ist 1 stets von 6 und 8 umgeben und 9 stets von 2 und 4. Daraus ergeben sich folgende mögliche magischen Quadrate: |
<math> | <math> | ||
| Zeile 122: | Zeile 127: | ||
Hierbei handelt es sich genau genommen nur um ein magisches Quadrat, welches lediglich gespiegelt und/oder rotiert wird. | Hierbei handelt es sich genau genommen nur um ein magisches Quadrat, welches lediglich gespiegelt und/oder rotiert wird. | ||
| + | |||
| + | === Magische Quadrate 4. Ordnung=== | ||
| + | Seit dem Jahr 1693 ist bekannt, dass sich 880 verschiedene magische Quadrate 4. Ordnung mit den Zahlen <math> 1,2,...,15,16</math> bilden lassen. Das wohl bekannteste <math> 4 \times 4</math> Quadrat ist ein magisches Quadrat, welches in dem Bild Melencolia I von Albrecht Dürer zu sehen ist. | ||
| + | |||
| + | <math> | ||
| + | \begin{bmatrix} | ||
| + | 16&3&2&13\\ | ||
| + | 5&10&11&8\\ | ||
| + | 9&6&7&12\\ | ||
| + | 4&15&14&1 | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | |||
| + | Das Quadrat ist symmetrisch und enthält in der letzten Zeile das Erscheinungsjahr 1514 des Kunstwerks. | ||
| + | |||
== Besondere magische Quadrate == | == Besondere magische Quadrate == | ||
===Pandiagonale magische Quadrate === | ===Pandiagonale magische Quadrate === | ||
[[Datei:Pandiagonal.png|mini|110x110px]] | [[Datei:Pandiagonal.png|mini|110x110px]] | ||
| − | Pandiagonale magische oder auch panmagische Quadrate erfüllen die zusätzliche Eigenschaft, dass die Summe der erweiterten Nebendiagonalen ebenfalls der magischen Summe entsprechen. Panmagische Quadrate sind gerader durch vier teilbarer Ordnung oder ungerader durch fünf teilbarer Ordnung. Somit ist ein pandiagonales magisches Quadrat mindestens von Ordnung vier. | + | Pandiagonale magische oder auch panmagische Quadrate erfüllen die zusätzliche Eigenschaft, dass die Summe der erweiterten Nebendiagonalen ebenfalls der magischen Summe entsprechen. Panmagische Quadrate sind von gerader, durch vier teilbarer Ordnung oder von ungerader, durch fünf teilbarer Ordnung. Somit ist ein pandiagonales magisches Quadrat mindestens von Ordnung vier. |
==== Beispiel==== | ==== Beispiel==== | ||
<math> | <math> | ||
| Zeile 160: | Zeile 180: | ||
</math> | </math> | ||
Es gilt <math>8+2=3+7=4+6=1+9=10 = 3^2+1 </math> | Es gilt <math>8+2=3+7=4+6=1+9=10 = 3^2+1 </math> | ||
| + | |||
| + | Insbesondere ist jede Spiegelung beziehungsweise Rotation dieses Quadrats symmetrisch. | ||
| + | |||
==== Beispiel 2==== | ==== Beispiel 2==== | ||
<math> | <math> | ||
| Zeile 172: | Zeile 195: | ||
=== Gerahmte magische Quadrate === | === Gerahmte magische Quadrate === | ||
Ein gerahmtes magisches Quadrat der Ordnung n umschließt ein magisches Quadrat der Ordnung n-2. Das heißt, wenn man die äußeren Spalten und Zeilen entfernt, erfüllt das restliche Quadrat noch immer die Eigenschaften eines magischen Quadrats. | Ein gerahmtes magisches Quadrat der Ordnung n umschließt ein magisches Quadrat der Ordnung n-2. Das heißt, wenn man die äußeren Spalten und Zeilen entfernt, erfüllt das restliche Quadrat noch immer die Eigenschaften eines magischen Quadrats. | ||
| − | ==== Beispiel ==== | + | ==== Beispiel==== |
| − | + | ||
| − | + | [[Datei:55mg.png|mini|alternativtext=|ohne|137x137px]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
ist ein magisches Quadrat der Ordnung 5. | ist ein magisches Quadrat der Ordnung 5. | ||
| − | + | ||
| − | + | [[Datei:33mq.png|mini|alternativtext=|ohne|104x104px]] | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
ist ein magisches Quadrat der Ordnung 3. | ist ein magisches Quadrat der Ordnung 3. | ||
| Zeile 196: | Zeile 207: | ||
# alle <math> 2 \times 2 -</math>Teilquadrate haben dieselbe Summe <math> s_{2 \times 2}=2(n^2+1)</math> | # alle <math> 2 \times 2 -</math>Teilquadrate haben dieselbe Summe <math> s_{2 \times 2}=2(n^2+1)</math> | ||
# das Quadrat hat die Ordnung <math> n=4k </math> mit <math> k \in \mathbb{N} </math> | # das Quadrat hat die Ordnung <math> n=4k </math> mit <math> k \in \mathbb{N} </math> | ||
| − | # summiert man zwei Elemente einer | + | # summiert man zwei Elemente einer erweiterten Neben- oder Hauptdiagonale, die den Abstand n/2 haben so ist dieser Wert stets gleich <math>d=n^2+1 </math> |
==== Beispiel ==== | ==== Beispiel ==== | ||
<math> | <math> | ||
| Zeile 210: | Zeile 221: | ||
#<math>1+16=8+9=...=15+2=7+10=4^2+1=17</math> | #<math>1+16=8+9=...=15+2=7+10=4^2+1=17</math> | ||
| − | ==Gruppeneigenschaften bei magischen | + | ==Gruppeneigenschaften bei symmetrischen magischen <math> 4 \times 4 </math>-Quadraten== |
| − | |||
Wir betrachten zunächst folgendes magisches 4x4-Quadrat, welches unsere Grundform <math>G</math> darstellen wird: | Wir betrachten zunächst folgendes magisches 4x4-Quadrat, welches unsere Grundform <math>G</math> darstellen wird: | ||
<gallery widths="200" heights="100"> | <gallery widths="200" heights="100"> | ||
Datei:Gruppemagischequadrate1.jpg | Datei:Gruppemagischequadrate1.jpg | ||
</gallery> | </gallery> | ||
| − | Durch Vertauschungen von Einträgen aus unserem magischen Quadrat <math>G</math>, erhalten wir | + | Durch Vertauschungen von Einträgen aus unserem magischen Quadrat <math>G</math>, erhalten wir die folgenden weiteren magischen Quadrate: |
1. Das magische Quadrat <math>A</math>. | 1. Das magische Quadrat <math>A</math>. | ||
| Zeile 236: | Zeile 246: | ||
</gallery> | </gallery> | ||
| − | + | Um eine Gruppe zu erhalten, wollen wir nun noch eine Verknüpfung definieren. Verknüpfen wir <math>A</math> mit <math>B</math>, so führen wir genau die Vertauschungen auf unsere Grundform <math>G</math> aus, die verwendet wurden, um <math>A</math> beziehungsweise <math>B</math> aus der Grundform <math>G</math> zu erhalten. Das heißt, wir vertauschen jeweils die grünen und die blauen Einträge in der entsprechenden Zeile. Es ergibt sich (wie man durch leichtes Nachrechnen herausfinden kann) das folgende magische Quadrat <math>AB </math>. | |
<gallery widths="200" heights="100"> | <gallery widths="200" heights="100"> | ||
Datei:Gruppemagischequadrate8.jpg | Datei:Gruppemagischequadrate8.jpg | ||
| Zeile 242: | Zeile 252: | ||
</gallery> | </gallery> | ||
| − | Analog funktionieren die Verknüpfungen <math> | + | Analog funktionieren die Verknüpfungen <math>AC </math> und <math>BC </math>. |
| − | Für <math> | + | Für <math>AC </math> führen wir also folgende Vertauschungen durch: |
<gallery widths="200" heights="100"> | <gallery widths="200" heights="100"> | ||
Datei:Gruppemagischequadrat9.jpg | Datei:Gruppemagischequadrat9.jpg | ||
| Zeile 249: | Zeile 259: | ||
</gallery> | </gallery> | ||
| − | <math> | + | <math>BC </math> erhalten wir dementsprechend durch folgendes Vorgehen: |
<gallery widths="200" heights="100"> | <gallery widths="200" heights="100"> | ||
Datei:Gruppemagischequadrate10.jpg | Datei:Gruppemagischequadrate10.jpg | ||
| Zeile 255: | Zeile 265: | ||
</gallery> | </gallery> | ||
| − | Da wir für <math> | + | Da wir für <math>AB </math> die gleichen Vertauschungen auf unsere Grundform <math>G </math> anwenden, wie für <math>BA </math>, gilt <math>AB = BA </math>. Analog folgt <math>AC = CA </math> und <math>BC = CB </math>. |
| − | Wollen wir <math> | + | Wollen wir <math>ABC </math> erhalten, so müssen wir alle Vertauschungen durchführen. Es ergibt sich also: |
<gallery widths="200" heights="100"> | <gallery widths="200" heights="100"> | ||
Datei:Gruppemagischequadrate11.jpg | Datei:Gruppemagischequadrate11.jpg | ||
Datei:Gruppemagischequadrate15.jpg | Datei:Gruppemagischequadrate15.jpg | ||
</gallery> | </gallery> | ||
| − | Nun können wir also folgende Verknüpfungstabelle betrachten und feststellen, dass die Menge <math>M = \{G, A, B, C, | + | Nun können wir also folgende Verknüpfungstabelle betrachten und feststellen, dass die Menge <math>M = \{G, A, B, C, AB, AC, BC, ABC \} </math> eine Gruppe darstellt, welche isomorph zu <math> (\mathbb{Z}/_{2\mathbb{Z}})^3 </math> ist. |
{| class="wikitable" | {| class="wikitable" | ||
|+ Verknüfungstabelle | |+ Verknüfungstabelle | ||
|- | |- | ||
| − | ! <math>\circ </math> !! <math>G </math>!! <math>A </math> !! <math>B </math> !! <math>C </math> !! <math> | + | ! <math>\circ </math> !! <math>G </math>!! <math>A </math> !! <math>B </math> !! <math>C </math> !! <math>AB </math> !! <math>AC </math> !! <math>BC </math> !! <math>ABC </math> |
|- | |- | ||
| − | | <math>G </math> | + | ! scope="col" | <math>G </math> |
| + | | <math>G </math> || <math>A </math> || <math>B </math> || <math>C </math> || <math>AB </math> || <math>AC </math>|| <math>BC </math>|| <math>ABC </math> | ||
|- | |- | ||
| − | | <math>A </math> | + | ! scope="col" | <math>A </math> |
| + | | <math>A </math> || <math>G </math> || <math>AB </math>|| <math>AC </math> || <math>B </math> || <math>C </math> || <math>ABC </math> || <math>BC </math> | ||
|- | |- | ||
| − | | <math>B </math> | + | ! scope="col" | <math>B </math> |
| + | | <math>B </math> || <math>AB </math> || <math>G </math> || <math>BC </math> || <math>A </math> || <math>ABC </math> || <math>C </math> || <math>AC </math> | ||
|- | |- | ||
| − | | <math>C </math> | + | ! scope="col" | <math>C </math> |
| + | | <math>C </math> || <math>AC </math> || <math>BC </math> || <math>G </math> || <math>ABC </math> || <math>A </math> || <math>B </math> || <math>AB </math> | ||
|- | |- | ||
| − | | <math> | + | ! scope="col" | <math>AB </math> |
| + | | <math>AB </math> || <math>B </math> || <math>A </math> || <math>ABC </math> || <math>G </math>|| <math>BC </math> || <math>AC </math> || <math>C </math> | ||
|- | |- | ||
| − | | <math> | + | ! scope="col" | <math>AC </math> |
| + | | <math>AC </math> || <math>C </math> || <math>ABC </math> || <math>A </math> || <math>BC </math> || <math>G </math> || <math>AB </math> || <math>B </math> | ||
|- | |- | ||
| − | | <math> | + | ! scope="col" | <math>BC </math> |
| + | | <math>BC </math> || <math>ABC </math> || <math>C </math> || <math>B </math> || <math>AC </math> || <math>AB </math> || <math>G </math> || <math>A </math> | ||
|- | |- | ||
| − | | <math> | + | ! scope="col" | <math>ABC </math> |
| + | | <math>ABC </math> || <math>BC </math> || <math>AC </math> || <math>AB </math> || <math>C </math> || <math>B </math> || <math>A </math> || <math>G </math> | ||
|} | |} | ||
Die Menge <math>M</math> bildet also eine Gruppe, wobei unsere Grundform <math>G</math> das neutrale Element darstellt und die Elemente selbstinvers sind, da zweifaches Vertauschen wieder die Grundform <math>G</math> ergibt. Assoziativität ist offensichtlich gegeben, da die Reihenfolge der Vertauschungen keine Rolle spielt. | Die Menge <math>M</math> bildet also eine Gruppe, wobei unsere Grundform <math>G</math> das neutrale Element darstellt und die Elemente selbstinvers sind, da zweifaches Vertauschen wieder die Grundform <math>G</math> ergibt. Assoziativität ist offensichtlich gegeben, da die Reihenfolge der Vertauschungen keine Rolle spielt. | ||
| − | + | Auch bei pandiagonalen magischen Quadraten können Gruppeneigenschaften beobachtet werden. Mehr dazu findet sich [https://www.michael-holzapfel.de/themen/mag_quadrat/mq-4/mq4.htm hier]. | |
| − | |||
| − | hier | ||
== Geschichte == | == Geschichte == | ||
| − | Es ist nicht bekannt, wann genau Wissenschaftler*innen begannen, sich mit magischen Quadraten zu beschäftigen, jedoch existieren bereits fortgeschrittene griechische Bücher über die Konstruktion magischer Quadrate aus dem 9. Jahrhundert. Im Arabischen Raum wurden im 11. und 12. Jahrhundert weitere Konstruktionsmöglichkeiten für gewöhnliche und auch pandiagonale magische Quadrate entdeckt. Erst im späten Mittelalter wurden arabische Texte über magische Quadrate in Europa auf Latein übersetzt, daraufhin wurden diese auch dort studiert. | + | Es ist nicht bekannt, wann genau Wissenschaftler*innen begannen, sich mit magischen Quadraten zu beschäftigen, jedoch existieren bereits fortgeschrittene griechische Bücher über die Konstruktion magischer Quadrate aus dem 9. Jahrhundert. Im Arabischen Raum wurden im 11. und 12. Jahrhundert weitere Konstruktionsmöglichkeiten für gewöhnliche und auch pandiagonale magische Quadrate entdeckt. Erst im späten Mittelalter wurden arabische Texte über magische Quadrate in Europa auf Latein übersetzt, daraufhin wurden diese auch dort studiert. In China und Indien können magische Quadrate aus dem ersten Jahrhundert vor Christus gefunden werden. Diese waren jedoch ausschließlich dritter Ordnung und erst im 13. Jahrhundert wurden dort magische Quadrate höherer Ordnung studiert, was sich auf arabische Texte zurückführen lässt. Eine Legende besagt, dass in China das erste magische Quadrat auf dem Rücken einer Schildkröte entdeckt wurde. |
== Konstruktion == | == Konstruktion == | ||
| − | Eine in Europa im 17. Jahrhundert durch Simon de la Loubère bekannt | + | Eine Konstruktionsmöglichkeit für magische Quadrate ungerader Ordnung wurde in Europa im 17. Jahrhundert durch Simon de la Loubère bekannt. Dafür trägt man die Zahlen <math> 1,.., n^2 </math> nacheinander wie folgt in das Quadrat ein: |
* Zunächst setzt man eine 1 in das mittlere Feld der oberen Reihe | * Zunächst setzt man eine 1 in das mittlere Feld der oberen Reihe | ||
* Nachdem man eine Zahl in ein Feld der oberen Reihe geschrieben hat, schreibt man die nächste in das unterste Feld der nächsten Spalte | * Nachdem man eine Zahl in ein Feld der oberen Reihe geschrieben hat, schreibt man die nächste in das unterste Feld der nächsten Spalte | ||
| Zeile 326: | Zeile 342: | ||
Joanna Schnorr<br /> | Joanna Schnorr<br /> | ||
Julia Bohn | Julia Bohn | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Aktuelle Version vom 27. September 2021, 10:54 Uhr
Definition
Ein magisches Quadrat der Ordnung n beschreibt eine n×n Matrix, in welcher paarweise verschiedene ganze Zahlen, häufig 1,..., [math]n^2 [/math], so angeordnet sind, dass die Summe der Hautdiagonalen-, Zeilen- und Spalteneinträge dem gleichen Wert entspricht. Diesen nennt man die magische Summe [math] s^* [/math].
Man spricht von einem semimagischen Quadrat, falls die Hauptdiagonalen nicht der magischen Summe entsprechen.
Für die Einträge [math] 1,.., n^2 [/math] entspricht die magische Summe [math] s^* = \frac{1}{n} \sum\limits_{k=1}^{n^2} k[/math].
Magische Quadrate niedriger Ordnung
Magische Quadrate 1. Ordnung
Magische Quadrate erster Ordnung besitzen nur einen Eintrag und sind somit trivial, da jede 1×1-Matrix die Eigenschaft eines magischen Quadrates erfüllt.
Magisches Quadrat 1-ter Ordnung [math] \begin{bmatrix} a \end{bmatrix} [/math] mit [math]a \in \mathbb{Z} [/math]
Magische Quadrate 2. Ordnung
Nach der oben aufgeführten Definition existieren keine magischen Quadrate zweiter Ordnung. Vernachlässigt man die Bedingung der paarweise verschiedenen Einträge, haben magische bzw. semimagische Quadrate folgende Form:
Magisches Quadrat 2-ter Ordnung [math] \begin{bmatrix} a & a \\ a & a \\ \end{bmatrix} [/math] mit [math]a \in \mathbb{Z} [/math]
Semimagisches Quadrat 2-ter Ordnung [math] \begin{bmatrix} a & b \\ b & a\\ \end{bmatrix} [/math] mit [math]a, b \in \mathbb{Z} [/math]
Magische Quadrate 3. Ordnung
Um den Aufbau eines magischen Quadrats dritter Ordnung zu verdeutlichen betrachten wir folgende Matrix
A= [math] \begin{bmatrix} a & b &c \\ d & e & f\\ g & h & i \\ \end{bmatrix} [/math] mit [math]a, b,...,i \in \mathbb{Z} [/math]
Sei [math]s^* \in \mathbb{Z}[/math] die magische Summe, so muss A folgende Eigenschaft erfüllen:
[math]s^* - e = a + i = b + h = c + g = f + d [/math]
Daraus lässt sich folgern, dass [math]a + b + ... + h + i = 4* (s^*-e)+e [/math] gilt.
Darüber hinaus gilt [math] a+b+...+h+i= 3s^*[/math], daraus folgt zusammen [math] s^* = 3e[/math].
Mit diesen Voraussetzungen, welche durch die Definition gegeben sind, lassen sich magische Quadrate der Ordnung 3 für die Zahlen 1,...,9 leicht konstruieren. Die magische Summe ergibt sich als [math] s^* = \frac{1}{3} \sum\limits_{k=1}^{9} k = 15[/math]. Somit gilt [math]e=5 [/math] und [math] 10 = a + i = b + h = c + g = f + d[/math]. Es gilt [math] 10 = 1+9 = 2+8 = 3 + 7= 4+6[/math]. Nehmen wir nun a=1 an, so erhalten wir [math]14 = b+c = d+g [/math] und [math] 6 = f+c =h+g[/math]. Da es je nur ein Paar gibt, welches gleich 14 bzw. gleich 6 ist, folgt, dass die Werte 1 und 9 nicht in einer der Ecken liegen können. Des Weiteren ist 1 stets von 6 und 8 umgeben und 9 stets von 2 und 4. Daraus ergeben sich folgende mögliche magischen Quadrate:
[math] \begin{bmatrix} 6 & 1 &8 \\ 7 & 5 & 3\\ 2 & 9 & 4 \\ \end{bmatrix} [/math] beziehungsweise durch Spiegelung [math] \begin{bmatrix} 8 & 1 &6 \\ 3 & 5 & 7\\ 4 & 9 & 2 \\ \end{bmatrix} [/math]
[math] \begin{bmatrix} 2 & 7 &6 \\ 9 & 5 & 1\\ 4 & 3 & 8 \\ \end{bmatrix} [/math] beziehungsweise durch Spiegelung [math] \begin{bmatrix} 4 & 3 &8 \\ 9 & 5 & 1\\ 2 & 7 & 6 \\ \end{bmatrix} [/math]
[math] \begin{bmatrix} 2 & 9 &4 \\ 7 & 5 & 3\\ 6 & 1 & 8 \\ \end{bmatrix} [/math] beziehungsweise durch Spiegelung [math] \begin{bmatrix} 4 & 9 &2 \\ 3 & 5 & 7\\ 8 & 1 & 6 \\ \end{bmatrix} [/math]
[math] \begin{bmatrix} 6 & 7 &2 \\ 1 & 5 & 9\\ 8 & 3 & 4 \\ \end{bmatrix} [/math] beziehungsweise durch Spiegelung [math] \begin{bmatrix} 8 & 3 &4 \\ 1 & 5 & 9\\ 6 & 7 & 2 \\ \end{bmatrix} [/math]
Hierbei handelt es sich genau genommen nur um ein magisches Quadrat, welches lediglich gespiegelt und/oder rotiert wird.
Magische Quadrate 4. Ordnung
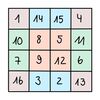
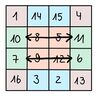
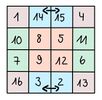
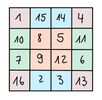
Seit dem Jahr 1693 ist bekannt, dass sich 880 verschiedene magische Quadrate 4. Ordnung mit den Zahlen [math] 1,2,...,15,16[/math] bilden lassen. Das wohl bekannteste [math] 4 \times 4[/math] Quadrat ist ein magisches Quadrat, welches in dem Bild Melencolia I von Albrecht Dürer zu sehen ist.
[math] \begin{bmatrix} 16&3&2&13\\ 5&10&11&8\\ 9&6&7&12\\ 4&15&14&1 \end{bmatrix} [/math]
Das Quadrat ist symmetrisch und enthält in der letzten Zeile das Erscheinungsjahr 1514 des Kunstwerks.
Besondere magische Quadrate
Pandiagonale magische Quadrate
Pandiagonale magische oder auch panmagische Quadrate erfüllen die zusätzliche Eigenschaft, dass die Summe der erweiterten Nebendiagonalen ebenfalls der magischen Summe entsprechen. Panmagische Quadrate sind von gerader, durch vier teilbarer Ordnung oder von ungerader, durch fünf teilbarer Ordnung. Somit ist ein pandiagonales magisches Quadrat mindestens von Ordnung vier.
Beispiel
[math] \begin{bmatrix} 25 & 64 & 2 & 39 \\ 8 & 33 & 31 & 58 \\ 63 & 26 & 40 & 1 \\ 34 & 7 & 57 & 32 \\ \end{bmatrix} [/math]
Es gilt [math] s^*= 25+33+40+32 = 130 [/math]
[math]8+26+57+39=130 [/math]
[math] 63+7+2+58=130[/math]
[math] 64+31+1+34=130[/math]
[math]8+64+57+1=130 [/math]
[math]63+33+2+32=130 [/math]
[math]7+40+58+25=130 [/math]
Symmetrische magische Quadrate
Man spricht von symmetrisch magischen Quadraten, falls Einträge, die um den Mittelpunkt zueinander punktsymmetrisch sind, summiert denselben Wert ergeben. Ist das Quadrat mit den Werten [math] 1,...,n^2[/math] gefüllt, so entspricht diese Summe [math] n^2+1[/math].
Beispiel 1
[math] \begin{bmatrix} 8 & 3 &4 \\ 1 & 5 & 9\\ 6 & 7 & 2 \\ \end{bmatrix} [/math] Es gilt [math]8+2=3+7=4+6=1+9=10 = 3^2+1 [/math]
Insbesondere ist jede Spiegelung beziehungsweise Rotation dieses Quadrats symmetrisch.
Beispiel 2
[math] \begin{bmatrix} 16 & 2 &3 & 13 \\ 5 & 11 & 10 & 8\\ 9 & 7 & 6 & 12 \\ 4 & 14 & 15 & 1 \end{bmatrix} [/math] Es gilt [math]16+1=11+6=13+4=7+10=17 = 4^2+1 [/math]
Gerahmte magische Quadrate
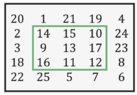
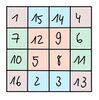
Ein gerahmtes magisches Quadrat der Ordnung n umschließt ein magisches Quadrat der Ordnung n-2. Das heißt, wenn man die äußeren Spalten und Zeilen entfernt, erfüllt das restliche Quadrat noch immer die Eigenschaften eines magischen Quadrats.
Beispiel
ist ein magisches Quadrat der Ordnung 5.
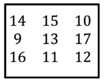
ist ein magisches Quadrat der Ordnung 3.
Supermagische Quadrate
Ein magisches Quadrat mit den Einträgen [math] 1,...,n^2[/math] heißt supermagisches Quadrat, falls es folgende Eigenschaften erfüllt:
- alle [math] 2 \times 2 -[/math]Teilquadrate haben dieselbe Summe [math] s_{2 \times 2}=2(n^2+1)[/math]
- das Quadrat hat die Ordnung [math] n=4k [/math] mit [math] k \in \mathbb{N} [/math]
- summiert man zwei Elemente einer erweiterten Neben- oder Hauptdiagonale, die den Abstand n/2 haben so ist dieser Wert stets gleich [math]d=n^2+1 [/math]
Beispiel
[math] \begin{bmatrix} 1&15&10&8\\ 12&6&3&13\\ 7&9&16&2\\ 14&4&5&11 \end{bmatrix} [/math]
- [math]1+15+12+6=10+8+3+13=...=9+16+4+5=6+3+9+16=2(4^2+1)=34[/math]
- das Quadrat hat die Ordnung 4
- [math]1+16=8+9=...=15+2=7+10=4^2+1=17[/math]
Gruppeneigenschaften bei symmetrischen magischen [math] 4 \times 4 [/math]-Quadraten
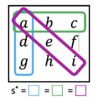
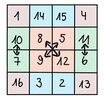
Wir betrachten zunächst folgendes magisches 4x4-Quadrat, welches unsere Grundform [math]G[/math] darstellen wird:
Durch Vertauschungen von Einträgen aus unserem magischen Quadrat [math]G[/math], erhalten wir die folgenden weiteren magischen Quadrate:
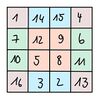
1. Das magische Quadrat [math]A[/math].
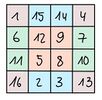
2. Das magische Quadrat [math]B[/math].
3. Das magische Quadrat [math]C[/math].
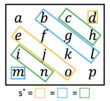
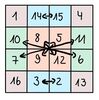
Um eine Gruppe zu erhalten, wollen wir nun noch eine Verknüpfung definieren. Verknüpfen wir [math]A[/math] mit [math]B[/math], so führen wir genau die Vertauschungen auf unsere Grundform [math]G[/math] aus, die verwendet wurden, um [math]A[/math] beziehungsweise [math]B[/math] aus der Grundform [math]G[/math] zu erhalten. Das heißt, wir vertauschen jeweils die grünen und die blauen Einträge in der entsprechenden Zeile. Es ergibt sich (wie man durch leichtes Nachrechnen herausfinden kann) das folgende magische Quadrat [math]AB [/math].
Analog funktionieren die Verknüpfungen [math]AC [/math] und [math]BC [/math]. Für [math]AC [/math] führen wir also folgende Vertauschungen durch:
[math]BC [/math] erhalten wir dementsprechend durch folgendes Vorgehen:
Da wir für [math]AB [/math] die gleichen Vertauschungen auf unsere Grundform [math]G [/math] anwenden, wie für [math]BA [/math], gilt [math]AB = BA [/math]. Analog folgt [math]AC = CA [/math] und [math]BC = CB [/math].
Wollen wir [math]ABC [/math] erhalten, so müssen wir alle Vertauschungen durchführen. Es ergibt sich also:
Nun können wir also folgende Verknüpfungstabelle betrachten und feststellen, dass die Menge [math]M = \{G, A, B, C, AB, AC, BC, ABC \} [/math] eine Gruppe darstellt, welche isomorph zu [math] (\mathbb{Z}/_{2\mathbb{Z}})^3 [/math] ist.
| [math]\circ [/math] | [math]G [/math] | [math]A [/math] | [math]B [/math] | [math]C [/math] | [math]AB [/math] | [math]AC [/math] | [math]BC [/math] | [math]ABC [/math] |
|---|---|---|---|---|---|---|---|---|
| [math]G [/math] | [math]G [/math] | [math]A [/math] | [math]B [/math] | [math]C [/math] | [math]AB [/math] | [math]AC [/math] | [math]BC [/math] | [math]ABC [/math] |
| [math]A [/math] | [math]A [/math] | [math]G [/math] | [math]AB [/math] | [math]AC [/math] | [math]B [/math] | [math]C [/math] | [math]ABC [/math] | [math]BC [/math] |
| [math]B [/math] | [math]B [/math] | [math]AB [/math] | [math]G [/math] | [math]BC [/math] | [math]A [/math] | [math]ABC [/math] | [math]C [/math] | [math]AC [/math] |
| [math]C [/math] | [math]C [/math] | [math]AC [/math] | [math]BC [/math] | [math]G [/math] | [math]ABC [/math] | [math]A [/math] | [math]B [/math] | [math]AB [/math] |
| [math]AB [/math] | [math]AB [/math] | [math]B [/math] | [math]A [/math] | [math]ABC [/math] | [math]G [/math] | [math]BC [/math] | [math]AC [/math] | [math]C [/math] |
| [math]AC [/math] | [math]AC [/math] | [math]C [/math] | [math]ABC [/math] | [math]A [/math] | [math]BC [/math] | [math]G [/math] | [math]AB [/math] | [math]B [/math] |
| [math]BC [/math] | [math]BC [/math] | [math]ABC [/math] | [math]C [/math] | [math]B [/math] | [math]AC [/math] | [math]AB [/math] | [math]G [/math] | [math]A [/math] |
| [math]ABC [/math] | [math]ABC [/math] | [math]BC [/math] | [math]AC [/math] | [math]AB [/math] | [math]C [/math] | [math]B [/math] | [math]A [/math] | [math]G [/math] |
Die Menge [math]M[/math] bildet also eine Gruppe, wobei unsere Grundform [math]G[/math] das neutrale Element darstellt und die Elemente selbstinvers sind, da zweifaches Vertauschen wieder die Grundform [math]G[/math] ergibt. Assoziativität ist offensichtlich gegeben, da die Reihenfolge der Vertauschungen keine Rolle spielt.
Auch bei pandiagonalen magischen Quadraten können Gruppeneigenschaften beobachtet werden. Mehr dazu findet sich hier.
Geschichte
Es ist nicht bekannt, wann genau Wissenschaftler*innen begannen, sich mit magischen Quadraten zu beschäftigen, jedoch existieren bereits fortgeschrittene griechische Bücher über die Konstruktion magischer Quadrate aus dem 9. Jahrhundert. Im Arabischen Raum wurden im 11. und 12. Jahrhundert weitere Konstruktionsmöglichkeiten für gewöhnliche und auch pandiagonale magische Quadrate entdeckt. Erst im späten Mittelalter wurden arabische Texte über magische Quadrate in Europa auf Latein übersetzt, daraufhin wurden diese auch dort studiert. In China und Indien können magische Quadrate aus dem ersten Jahrhundert vor Christus gefunden werden. Diese waren jedoch ausschließlich dritter Ordnung und erst im 13. Jahrhundert wurden dort magische Quadrate höherer Ordnung studiert, was sich auf arabische Texte zurückführen lässt. Eine Legende besagt, dass in China das erste magische Quadrat auf dem Rücken einer Schildkröte entdeckt wurde.
Konstruktion
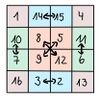
Eine Konstruktionsmöglichkeit für magische Quadrate ungerader Ordnung wurde in Europa im 17. Jahrhundert durch Simon de la Loubère bekannt. Dafür trägt man die Zahlen [math] 1,.., n^2 [/math] nacheinander wie folgt in das Quadrat ein:
- Zunächst setzt man eine 1 in das mittlere Feld der oberen Reihe
- Nachdem man eine Zahl in ein Feld der oberen Reihe geschrieben hat, schreibt man die nächste in das unterste Feld der nächsten Spalte
- Wenn man eine Zahl in das letzte Feld einer Reihe geschrieben hat, so schreibt man die nächste in das erste Feld der Reihe darüber
- In allen anderen Fällen schreibt man die nächste Zahl in das Feld rechts über der zuvor geschriebenen Zahl
- Falls ein Feld bereits besetzt ist, so schreibt man die nächste Zahl in das Feld unter der zuvor geschriebenen Zahl
- Beispiel eines magischen Quadrats der Größe 3x3
Weblinks
https://www.magic-squares.info/
https://www.michael-holzapfel.de/themen/mag_quadrat/mq-4/mq4.htm
Einzelnachweise/Literaturverzeichnis
Beck, Matthias; Robins, Sinai: Das Kontinuum diskret berechnen. Kapitel 6.
Sesiano, Jacques: Magic Squares-Their History and Construction from Ancient Times to AD 1600.
AutorInnen
Julia Renner
Joanna Schnorr
Julia Bohn