Gödelsche Unvollständigkeitssätze: Unterschied zwischen den Versionen
Fx255 (Diskussion | Beiträge) |
|||
| (77 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | Der '''Gödelsche Unvollständigkeitssatz''' ist einer der wichtigsten Sätze der modernen Logik. Er beschäftigt sich mit der Ableitbarkeit von Aussagen in formalen Systemen. Der Satz zeigt die Grenzen der formalen Systeme ab einer bestimmten Leistungsfähigkeit auf. Er weist nach, dass es in hinreichend starken Systemen, wie der Arithmetik, Aussagen geben muss, die man formal weder beweisen noch widerlegen kann. Der Satz beweist damit die Undurchführbarkeit des Hilbertprogramms, das von David Hilbert unter anderem begründet wurde, um die Widerspruchsfreiheit der Mathematik zu beweisen.<ref>https://de.wikipedia.org/wiki/G%C3%B6delscher_Unvollst%C3%A4ndigkeitssatz</ref>[[Datei:1925 kurt gödel.png|alternativtext=Portrait von Kurt Gödel|mini|194x194px|Kurt Gödel]] | ||
| + | |||
== [https://de.wikipedia.org/wiki/Kurt_G%C3%B6del Kurt Gödel] == | == [https://de.wikipedia.org/wiki/Kurt_G%C3%B6del Kurt Gödel] == | ||
Kurt Gödel war ein Mathematiker des 20.Jahrhunderts, der sich viel mit der Lehre der Logik in der Mathematik beschäftigte. So suchte er auch nach Antworten auf [https://de.wikipedia.org/wiki/Hilbertsche_Probleme#Die_Probleme Hilberts Probleme und Fragen]. Als Antwort auf das zweite Problem, "Sind die arithmetischen Axiome widerspruchsfrei?", entstanden die Unvollständigkeitssätze Gödels, auf welche im weiteren eingegangen wird. | Kurt Gödel war ein Mathematiker des 20.Jahrhunderts, der sich viel mit der Lehre der Logik in der Mathematik beschäftigte. So suchte er auch nach Antworten auf [https://de.wikipedia.org/wiki/Hilbertsche_Probleme#Die_Probleme Hilberts Probleme und Fragen]. Als Antwort auf das zweite Problem, "Sind die arithmetischen Axiome widerspruchsfrei?", entstanden die Unvollständigkeitssätze Gödels, auf welche im weiteren eingegangen wird. | ||
| − | |||
== Gödelsche Unvollständigkeitssätze == | == Gödelsche Unvollständigkeitssätze == | ||
| − | Veröffentlicht im Jahr 1931 besagen die | + | Veröffentlicht im Jahr 1931 besagen die Unvollständigkeitssätze als ganzes, dass es in hinreichend starken Systemen (Bsp. [https://de.wikipedia.org/wiki/Arithmetik Arithmetik]) Aussagen geben kann, von denen man weder beweisen kann, dass sie wahr sind, noch diese widerlegen kann. |
| − | So besagt Gödels erster Unvollständigkeitssatz, dass es in allen widerspruchsfreien Systemen | + | So besagt Gödels erster Unvollständigkeitssatz, dass es in allen widerspruchsfreien Systemen Aussagen gibt, deren Wahrheitsgehalt weder be- noch wiederlegt werden kann. |
Der zweite Satz besagt, dass man in widerspruchsfreien und hinreichend starken Systemen deren Widerspruchsfreiheit nicht beweisen kann. | Der zweite Satz besagt, dass man in widerspruchsfreien und hinreichend starken Systemen deren Widerspruchsfreiheit nicht beweisen kann. | ||
Wir legen im folgenden den Fokus auf den ersten Unvollständigkeitssatz. | Wir legen im folgenden den Fokus auf den ersten Unvollständigkeitssatz. | ||
| − | Betrachtet man die Aussage dessen, so stellt sich die Frage, | + | Betrachtet man die Aussage dessen, so stellt sich die Frage: Was mache ich, wenn ich an einer wahren Aussage forsche, aber nicht weiß, ob sie überhapt belegbar ist? Hierzu ein kurzer geschichtlicher Abriss. |
===Bisheriges Verständnis=== | ===Bisheriges Verständnis=== | ||
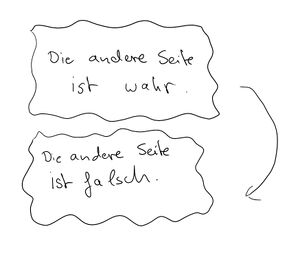
| + | [[Datei:Wahr und Falsch.jpg|alternativtext="Die andere Seite ist wahr/falsch"|mini|Wahr und falsch]] | ||
| + | Seit dem antiken Griechenland ist man davon ausgegangen, dass alles mathematisch Wahre auch innerhalb der Mathematik bewiesen werden kann. Gödel hat jedoch mit seinen Unvollständigkeitssätzen gezeigt, dass "wahr" und "beweisbar" nicht zwingend zusammenhängen müssen. | ||
| + | Ein Beispiel dafür, dass man nicht sagen, oder besser beweisen kann, was wahr und was falsch ist, können wir aus unserem Alltag konstruieren. Betrachtet man ein Blatt Papier und schreibt auf die eine Seite, “Die andere Seite des Papiers ist wahr”, und auf jene angesprochene andere Seite, “Die andere Seite der Papiers ist falsch”, so findet man sich beim Versuch zu ergründen, welche Aussage nun stimmt, in einem Dilemma wieder, da man nicht sagen kann, welche Seite des Papiers nun “Recht” hat. Dies ist für uns im Alltag kein Problem, da wir nicht davon ausgehen, dass alle Aussagen wahr oder falsch sein müssen, oder sogar beweisbar wahr sind. Gödel sagt jedoch, dass ein solches Dilemma auch in der Mathematik auftreten kann - nun wird daraus in der Mathematik tatsächlich ein Problem. Denn wir verlangen von mathematischen Systemen Konsistenz, das heißt, dass jede Aussage entweder wahr oder falsch ist. In anderen Worten sollen mathematische Systeme widerspruchsfrei sein. Gödel hinterfragt also die Vollständigkeit der Mathematik und zeigt letztendlich, dass ausreichend komplexe mathematische Systeme unter Annahme von Konsistenz nicht [https://de.wikipedia.org/wiki/G%C3%B6delscher_Unvollst%C3%A4ndigkeitssatz#:~:text=folgt.-,Ein%20System,folgt.,-G%C3%B6dels%20S%C3%A4tze%5BBearbeiten vollständig] sein können. | ||
| + | |||
| + | Wie bereits erwähnt, war dieser Tatbestand der Vollständigkeit der Mathematik eines der Probleme Hilberts: “Prove Math is consistent”. | ||
| + | Kurt Gödel hat dieses Problem mit seinem Unvollständigkeitssatz gelöst, oder besser gesagt widerlegt, indem er beweisen hat, dass Mathematik nicht vollständig ist. | ||
| + | |||
| + | Doch genug der Geschichtsstunde, betrachten wir nun, was Gödel eigentlich herausgefunden hat. | ||
| + | |||
| + | ===Versuchte Erklärung der Beweisidee=== | ||
| + | |||
| + | Um den Beweis von Gödel zu verstehen, müssen wir zuerst einen kurzen Blick auf die generelle Beweisstruktur der heutigen Mathematik werfen. Die Grundlage der verwendeten Mathematik sind festgelegte [https://de.wikipedia.org/wiki/Axiom Axiome], wie z.B.: "Mengen sind genau dann gleich, wenn sie dieselben Elemente enthalten"<ref>https://de.wikipedia.org/wiki/Zermelo-Fraenkel-Mengenlehre#:~:text=1.%20Extensionalit%C3%A4tsaxiom%3A%20Mengen%20sind%20genau%20dann%20gleich%2C%20wenn%20sie%20dieselben%20Elemente%20enthalten.</ref>. Hat man nun eine mathematische Aussage, so versucht man diese aus den festgelegten Axiomen zu beweisen oder zu widerlegen. Findet man dabei etwas, das immer gültig ist, jedoch nicht bewiesen werden kann, so macht man es zu einem neuen Axiom, einem als wahr angesehenen Grundbaustein der Mathematik. Bisher war man also der Ansicht, dass wenn man nur genügend Axiome hat, alle Aussagen beweisbar sind, oder besser gesagt, irgendwann alle Axiome gefunden sind und alles bewiesen werden kann. Kurzum, man ist davon ausgegangen, dass die Mathematik irgendwann vollständig abgeschlossen ist. | ||
| + | |||
| + | Betrachten wir nun, was Gödel in seinem Beweis macht. Seine Idee war es, die Mathematik in Zahlen umzuformen und dann, durch beispielsweise Primfaktorzerlegung, allen Aussagen Nummern zuzuordnen, die unfehlbar nach Dekodierung auf die Nummern der Axiome zurückführen, und somit die Aussagen beweisen. Als erstes führt er hierfür den sogenannten Gödelcode, oder auch [https://en.wikipedia.org/wiki/G%C3%B6del_numbering Gödelnumbering] ein, womit er jedem Axiom und jeder Aussage, nach einem festgelegten Prinzip eine Nummer, die Gödelnummer, zuordnet. Diese Nummern werden dabei sehr groß, da jede Aussage ihre eigene individuelle Gödelnummer bekommt. Ein Beispiel aus der heutigen technologisierten Welt ist der [https://de.wikipedia.org/wiki/American_Standard_Code_for_Information_Interchange Ascii-Code], der jedem Buchstaben, Sonderzeichen oder Smiley eine bestimmte vom Computer auslesbare Kombination gibt. Wie auch beim Ascii-Code sorgt eine Zusammensetzung der einzelnen Axiome oder auch Aussagen für eine größere Nummer. So kann beispielsweise ein Smiley durch Kombination mit einer Farbe in unterschiedlichen Gesichtsfarben dargestellt werden. Damit hat Gödel sein Primärziel erreicht. Er kann nun mit Mathematik, als festgelegtes äußeres System Aussagen über die in Gödelnummern festgelegte Mathematik treffen. Vereinfacht gesagt, man kann aus den Nummern bestimmen, ob eine Aussage aus den Axiomsnummern zusammengesetzt werden und damit bewiesen werden kann oder nicht. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | Hier lohnt es sich ein kurzes Beispiel anzusehen. In dem System von Gödel das von Nagel und Newman verwendet wird, ist die 0 eine 6 und das Ist-Gleich-Zeichen die 5. Will man also 0=0 in dem System schreiben so findet sich das unter der Nummer 2<sup>6</sup> * 3<sup>5</sup> * 5<sup>6</sup> = 243,000,000. | |
| − | |||
| − | |||
| − | + | Kommen wir nun zu einer Aussage, die das ganze problematisch werden lässt und zeigt, dass Mathematik eben doch nicht vollständig ist und es weitergeführt auch niemals sein wird. Diese Aussage lautet: “Diese Aussage kann nicht aus den Axiomen bewiesen werden”. Gehen wir nun als erstes davon aus, dass diese Aussage falsch ist, so muss sie aus den Axiomen beweisbar sein. Dies wäre aber ein Widerspruch, denn wir nehmen an, dass in widerspruchsfreien Systemen nur wahre Aussage bewiesen werden können. Ist dies nicht der Fall, so muss die Aussage, da sie mit Mathematik beschrieben wurde, zwingend richtig sein, da es nach unserem Verständnis in der Mathematik beim rechnen, in diesem Fall mit den Gödelnummern, nur Richtig oder Falsch gibt. Wir haben also in unserem mathematischen System eine Aussage gefunden, die zwar richtig ist, jedoch nicht aus den Axiomen nachgewiesen werden kann. Wichtig hierbei ist, dass wir diese Aussage nur als wahr klassifizieren können, da wir die Mathematik von außerhalb mit sich selbst betrachtet haben. In dem eigentlich betrachteten System, der in den Gödelnummern festgelegten Mathematik, in dem die Aussage “lebt”, kann diese weder widerlegt noch bewiesen werden, obwohl wir von außerhalb wissen, dass sie wahr ist. Wir haben also eine Aussage wahren Inhalts gefunden, die innerhalb eines abgeschlossenen mathematischen Systems nicht bewiesen werden kann. Wir haben bereits erwähnt, dass eine solche Aussage dann als Axiom festgelegt wird. Wenn wir erneut eine solche Aussage finden, dann wird auch diese als Axiom mit aufgenommen, bis es nicht mehr möglich ist eine derartige Aussage zu finden. Nun hat Gödel gezeigt, dass es unendlich viele Aussagen dieses Typus gibt, also die Mathematik niemals vollständig sein kann. Damit wird es immer Aussagen geben die zwar wahr sind, jedoch nicht bewiesen werden können. | |
| + | |||
| + | ===Bedeutung für Mathematiker heute=== | ||
| + | |||
| + | Betrachtet man nun die Auswirkungen von Gödels Unvollständigkeitssätzen auf die heutige Zeit, so fällt auf, dass diese obwohl sie die Mathematik in ihren Grundfesten erschüttert haben, für die eigentliche Forschung an aktuellen Problemen nur bedingte Auswirkung haben. Man kann nicht mehr davon ausgehen für alles eine Lösung zu finden und die Mathematik wird niemals fertig sein. Dies ist auch gut so, denn wenn beispielsweise jeder Mathematiker nach einer Woche sagen würde, "Das Forschungsgebiet taugt nichts, das ist doch wahrscheinlich nicht beweisbar", dann würde die Mathematik als solche keine Fortschritte mehr machen. Somit ändert Gödels Feststellung der unvollständigen Mathematik an der aktuellen Forschung und Problemlösung nur in sofern etwas, dass man immer im Kopf behalten sollte, dass es möglicherweise in letzter Konsequenz doch keinen Beweis der These gibt, und man vielleicht in Betracht ziehen sollte zu überprüfen, ob die These überhaupt beweisbar ist. Auf der anderen Seite hat Gödel jedoch damit ein neues umso unvorhersehbareres Forschungsgebiet eröffnet, welches in der Vergangenheit bereits erstaunliche Ergebnisse geliefert hat. | ||
| + | |||
| + | ==== Neue Beweismethode ==== | ||
| + | |||
| + | Eine Folge Gödels Ergebnisse, welche man vielleicht als etwas seltsam bezeichnen könnte, ist die Möglichkeit zu beweisen, dass etwas innerhalb von einem Axiomsystem nicht widerlegbar oder nicht beweisbar ist. Dies ermöglicht eine neue Beweismethode. | ||
| + | Sollte man zum Beispiel beweisen können, dass [https://de.wikipedia.org/wiki/Riemannsche_Vermutung#:~:text=Die%20Riemannsche%20Vermutung%20oder%20Riemannsche,unter%20einer%20gegebenen%20Gr%C3%B6%C3%9Fe%20formuliert. Die Riemannsche Vermutung] innerhalb unseres Axiomsystems nicht entscheidbar ist, würde dies allgemein implizieren, dass die Vermutung wahr sein muss. Denn wäre sie falsch, dann gäbe es sofort eine implementierbare Methode in unserem System, welche ein Gegenbeispiel, d.h. eine nichttriviale Null außer den kritischen Streifen, finden kann. | ||
| + | |||
| + | == Beispiele für Gödels Sätze== | ||
| + | |||
| + | Nachdem wir nun den Inhalt sowie das Konzept der Unvollständigkeitssätze betrachtet haben, möchten wir abschließend noch den Blick auf zwei Beispiele für das Unvorhersagbare, oder auch Unbeweisbare liefern. | ||
| + | |||
| + | |||
| + | === Kontinuumshypothese === | ||
| + | |||
| + | ==== Die Frage ==== | ||
| + | |||
| + | Die [https://de.wikipedia.org/wiki/Kontinuumshypothese#:~:text=Die%20Kontinuumshypothese%20wurde%201878%20vom,der%20Menge%20der%20reellen%20Zahlen. Kontinuumshypothese] wurde 1878 vom Mathematiker [https://de.wikipedia.org/wiki/Georg_Cantor Georg Cantor] aufgestellt und beinhaltet eine Vermutung über die Mächtigkeit des Kontinuums, also der Menge der reellen Zahlen. | ||
| + | |||
| + | In der einfachen Formulierung besagt die Hypothese, dass es keine Menge gibt, deren Mächtigkeit zwischen der Mächtigkeit der natürlichen Zahlen und der Mächtigkeit der reellen Zahlen liegt. | ||
| + | |||
| + | ==== Lösung aber keine Antwort ==== | ||
| + | |||
| + | Gödel bewies 1938, dass unter der Annahme, dass die [https://de.wikipedia.org/wiki/Zermelo-Fraenkel-Mengenlehre Zermelo-Fraenkel-Mengenlehre] mit dem Auswahlaxiom (ZFC) widerspruchsfrei ist, auch die Kontinuumshypothese widerspruchsfrei ist. Also, dass man im Rahmen der ZFC die Kontinuumshypothese nicht widerlegen kann. Ungefähr zwanzig Jahre später zeigte Paul Cohen dann das Gegenteil, nämlich dass man mit ZFC die Kontinuumshypothese nicht beweisen kann. Insgesamt war somit die Lösung zu Cantors Fragestellung, dass die Kontinuumshypothese im Rahmen von ZFC nicht lösbar ist. Da sowohl die Kontinuumshypothese und ihre Negation beide ohne Widerspruch ZFC als Axiome erweitern konnten, sind sie eines der ersten relevanten Beispiele für Gödels ersten Unvollständigkeitssatz. | ||
| + | |||
| + | ==== Qual der Wahl ==== | ||
| + | |||
| + | Die Arbeit um die Kontinuumshypothese war damit aber längst nicht fertig. Denn die Frage: "Was ist die genaue Mächtigkeit des Kontinuums?" welche in der Kontinuumshypothese an sich gestellt wurde, blieb immer noch unbeantwortet. Und da ZFC sich als eine nicht ausreichende Liste an Axiomen um diese Frage zu beantworten herausgestellt hat, muss man entscheiden, mit welchen Axiomen ZFC ergänzt werden soll, um die Frage beantworten zu können. | ||
| + | Das ist ein gutes Beispiel für die Auswirkungen von Gödels Gesetzten. Nur weil eine Frage innerhalb eines Axiomensystems nicht beantwortet werden kann, muss dies nicht heißen, dass keine Antwort existiert. Dies wird auch deutlich in der Aussage von [https://mathematics.huji.ac.il/people/menachem-magidor Menachem Magidor]: “The axioms do not settle these problems so we must extend them to a richer axiom system.”<ref>https://www.quantamagazine.org/how-many-numbers-exist-infinity-proof-moves-math-closer-to-an-answer-20210715/#:~:text=The%20axioms%20do%20not%20settle%20these%20problems%2C%E2%80%9D%20said%20Magidor%2C%20so%20%E2%80%9Cwe%20must%20extend%20them%20to%20a%20richer%20axiom%20system.%E2%80%9D%20It%E2%80%99s%20ZFC%20as%20a%20means%20to%20mathematical%20truth%20that%E2%80%99s%20lacking%20%E2%80%94%20not%20truth%20itself.</ref> Hier fängt aber die Diskussion an, womit das System ergänzt werden soll. Die Suche nach “richtigen” Axiomen stellt sich als besonders schwer dar, denn, wie Gödel bewiesen hat, wird jedes ausreichend komplexe Axiomensystem unvollständig sein. Somit gibt es keine “richtigen” Axiomen und die Auswahl zwischen zwei besonders guten Vorschlägen kann sehr schwer sein. Im Fall der Kontinuumshypothese ist das aktuell ein offenes Problem. | ||
| + | |||
| + | ==== Neuer Fortschritt ==== | ||
| + | |||
| + | Zwei gute Axiome haben sich herausgestellt, das “Martin’s maximum++" und “(*)”. Martin's maximum++ ist eine technische Variation vom Martin's maximum<ref>https://www.quantamagazine.org/how-many-numbers-exist-infinity-proof-moves-math-closer-to-an-answer-20210715/#:~:text=In%201988%2C%20Magidor%2C%20Matthew%20Foreman%20and%20Saharon%20Shelah%20took%20this%20ethos%20to%20its%20logical%20conclusion%20by%20posing%20Martin%E2%80%99s%20maximum%2C%20which%20says%20that%20anything%20you%20can%20conceive%20of%20using%20any%20forcing%20procedure%20will%20be%20a%20true%20mathematical%20entity%2C%20so%20long%20as%20the%20procedure%20satisfies%20a%20certain%20consistency%20condition.</ref> und (*)<ref>https://www.quantamagazine.org/how-many-numbers-exist-infinity-proof-moves-math-closer-to-an-answer-20210715/#:~:text=Woodin%20proposed%20another,axiom%20of%20choice.</ref> (ausgesprochen "Star" bzw. "Stern"), ein Axiom welches sich auf eine Mengenlehre bezieht, die neun der Zermelo-Fraenkel Axiome erfüllt zusammen mit dem Axiom der Determiniertheit anstatt des Axioms der Wahl. Jedoch hat man die beiden Axiome bisher als sich gegenseitig ausschließend verstanden. Nun ergaben Forschungsergebnisse von Ralf Schindler und [https://archive.uea.ac.uk/~bfe12ncu/ David Asperó] einen Grund, um anders zu denken. Die beide Mathematiker behaupten, sie könnten eine Implikation zwischen den beiden Axiomen beweisen. Sollte der Versuch gelingen, würden sich die Aussagen nicht widersprechen und man könnte eine wählen und als Axiom festlegen, ohne die Vorteile der anderen aufgeben zu müssen. Sollte das passieren und das neue Axiom aufgenommen sein, so wäre die Mächtigkeit des Kontinuums als Aleph 2 festgelegt. Auf der anderen Seite arbeitet [https://www.math.harvard.edu/people/woodin-hugh/ Hugh Woodin] an einer Lösung welche die Mächtigkeit auf Aleph 1 setzen würde. Sein sogenanntes “Ultimate L” Modell sollte eine Verallgemeinerung von Gödels Mengenlehre sein. | ||
| + | |||
| + | |||
| + | |||
| + | ===Game of Life=== | ||
| + | |||
| + | ==== Grundlagen ==== | ||
| + | |||
| + | Ein weiteres Beispiel ist das “Game of Life” von [https://de.wikipedia.org/wiki/John_Horton_Conway John Horton Conway]. Bei diesem "Kein Spieler Spiel", gibt es ein unendliches, in quadratische Felder eingeteiltes Spielbrett, auf welchem zu Beginn beliebig Spielsteine platziert werden können. Dann wird das Spiel oder die “Simulation” gestartet. Jede Runde entstehen oder verschwinden Spielsteine. Hierbei wird ein Feld, auf welchem ein Spielstein liegt, als lebend und ein Feld ohne Spielstein als tot bezeichnet. Außerdem hat jedes Feld 8 Nachbarn. Nun verändert sich das Spielfeld, bzw. die Verteilung der Stein zu Beginn jeder Runde nach folgenden Regeln, die simultan für alle Felder ausgeführt werden: | ||
| + | |||
| + | # Eine totes Feld mit genau drei lebenden Nachbarn wird in der folgenden Runde neu “geboren”, also mit einem Spielstein besetzt. | ||
| + | # | ||
| + | # Lebende Felder mit weniger als zwei lebenden Nachbarn sterben in der folgenden Runde an Einsamkeit, also wird der Spielstein entfernt. | ||
| + | # | ||
| + | # Ein lebendiges Feld mit zwei oder drei lebenden Nachbarfeldern bleibt in der Folgegeneration am Leben. Es passiert also nichts mit dem Feld. | ||
| + | # | ||
| + | # Lebende Felder mit mehr als drei lebenden Nachbarfeldern sterben in der Folgegeneration an Überbevölkerung, also wird der Spielstein entfernt. | ||
| + | # | ||
| + | # Tote Felder ohne Nachbarn bleiben tot. | ||
| + | |||
| + | |||
| + | Jede Runde ist im übertragenen Sinne eine Generation. Nun wird das Spiel gestartet und das Spielfeld verändert sich in jeder Runde. Hierbei können aus unterschiedlichen Anfangskonstellationen unterschiedliche Formationen entstehen. Dabei gibt es prinzipiell drei mögliche Ausgänge der Simulation. | ||
| + | |||
| + | |||
| + | * Es entstehen konstante Konstellationen, die nach einer gewissen Anzahl wieder in einer bereits durchlaufenen Konstellation auftauchen. Diese können statisch sein, oder sich über das Feld bewegen. | ||
| + | * | ||
| + | * Es werden immer mehr Felder besetzt. | ||
| + | * | ||
| + | * Es sterben immer mehr Zellen, bis das Spielfeld letztlich leer/tot ist. | ||
| + | |||
| + | |||
| + | ==== Beispiele: ==== | ||
| + | |||
| + | =====Konstante Konstellationen:===== | ||
| + | |||
| + | *Statische: <gallery caption="Statische Konstellationen"> | ||
| + | Datei:Statik 1.jpg|Statische Konstellation 1 | ||
| + | Datei:Statik 2.jpg|Statische Konstellation 2 | ||
| + | Datei:Statik 3.jpg|Statische Konstellation 3 | ||
| + | Datei:Statik 4.jpg|Statische Konstellation 4 | ||
| + | Datei:Statik 5.jpg|Statische Konstellation 5 | ||
| + | Datei:Statik 6.jpg|Statische Konstellation 6 | ||
| + | </gallery> | ||
| + | * | ||
| + | *Oszillierende:<gallery> | ||
| + | Datei:2g3 o01.gif|Blinker | ||
| + | Datei:2g3 2-laser.gif|2 Laser | ||
| + | Datei:2g3 fontaine.gif|Fontäne | ||
| + | Datei:Pulsator.gif|Pulsator | ||
| + | </gallery> | ||
| + | * | ||
| + | *Wandernde/Raumschiffe:<gallery> | ||
| + | Datei:Glider.gif|Gleiter | ||
| + | </gallery><gallery widths="720" heights="120"> | ||
| + | Datei:2g3 segler.gif|Segler | ||
| + | </gallery> | ||
| + | |||
| + | =====Erzeugende Konstellationen===== | ||
| + | *Gleiterkanone:<gallery widths="360"> | ||
| + | Datei:CONWAY-3 Glider Gun Glider Eater.gif|Gleiterkanone mit Gleiterfresser | ||
| + | </gallery> | ||
| + | |||
| + | =====Sterbende Konstellationen===== | ||
| + | Verschiedene Möglichkeiten, Beispiel: einzelnes Feld | ||
| + | |||
| + | Das Unvorhersagbare an diesem Beispiel ist, dass man aus der Anfangskonstellation nicht vorhersagen kann was passieren wird, ausgenommen bei bereits bekannten Konstellationen. Um also herauszufinden was mit einer bestimmten Konstellation passiert, muss man diese solange laufen lassen, bis man eine statische oder oszillierende, eine nach festem Prinzip wachsende, oder eine nicht mehr existente Konstellation gefunden hat. Hierbei lässt sich nicht sagen: "Diese Konstellation hat jetzt 100 Generationen überlebt, deshalb überlebt sie für immer". So kann eine riesige Konstellation, die nach einer Million Lebenszyklen noch lebt, nach beispielsweise einer weiteren Million Generationen vollständig verschwunden sein. | ||
| + | |||
| + | Hierfür ein Beispiel, das auch der Intuition widerspricht, ist das r-Pentomino, welches am Anfang ein chaotisch wachsendes Muster aufweist und nach 1103 Generationen dann ein fast vollständig statisch oder oszillierendes Spielfeld hinterlässt. Ausnahme sind wenige wegfliegende Gleiter. | ||
| + | |||
| + | <gallery> | ||
| + | Datei:R-Pentomino.jpg|R-Pentomino | ||
| + | Datei:Game of life f pent.gif|Animation über 1200 Generationen | ||
| + | </gallery> | ||
| + | |||
| + | Wer möchte kann es hier selbst versuchen: [https://playgameoflife.com/ Game of Life spielen] | ||
| + | |||
| + | =====Was das Game of Life kann===== | ||
| + | |||
| + | Man hat inzwischen festgestellt, dass es möglich ist, in Conways Game of Life, Schaltungen wie "und" und "oder" zu bauen, und es sogar gelungen ist, das Game of Life im Game of Life zu bauen, was bedeutet, dass das Game of Life "Turing complete" ist. Dies geht nun aber tatsächlich weit über das eigentliche Thema der Unvollständigkeitssätze hinaus. Deshalb wollen wir das Thema hier nicht weiter ausführen. | ||
| + | |||
| + | == Quellen == | ||
| + | |||
| + | === Externe Quellen === | ||
| + | * [https://www.youtube.com/watch?v=O4ndIDcDSGc&ab_channel=Numberphilev Numberphile - Gödel's Incompleteness Theorem] | ||
| + | |||
| + | * [https://www.youtube.com/watch?v=mccoBBf0VDM&ab_channel=Numberphile Numberphile - Gödel's Incompleteness (extra footage 1)] | ||
| + | |||
| + | * [https://www.youtube.com/watch?v=HeQX2HjkcNo&ab_channel=Veritasium Veritasium - Math Has a Fatal Flaw] | ||
| + | |||
| + | * [https://www.quantamagazine.org/how-many-numbers-exist-infinity-proof-moves-math-closer-to-an-answer-20210715/ Quanta Magazine - How Many Numbers Exist? Infinity Proof Moves Math Closer to an Answer] | ||
| + | |||
| + | * [https://de.wikipedia.org/wiki/Conways_Spiel_des_Lebens Wikipedia - Conways_Spiel_des_Lebens] | ||
| + | |||
| + | * [https://de.wikipedia.org/wiki/G%C3%B6delscher_Unvollst%C3%A4ndigkeitssatz Wikipedia - Gödelscher Unvollständigkeitssatz] | ||
| + | |||
| + | * [https://de.wikipedia.org/wiki/Kurt_G%C3%B6del Wikipedia - Kurt Gödel] | ||
| + | |||
| + | * [https://www.youtube.com/watch?v=Kk2MH9O4pXY&t=1229s Alan Zucconi - Let’s BUILD a COMPUTER in CONWAY's GAME of LIFE ⠠⠵] | ||
| + | |||
| + | == Autoren == | ||
| − | + | Kaspar Haas | |
| − | + | Leon-Josip Dzojic | |
| + | <references /> | ||
Aktuelle Version vom 30. September 2021, 23:01 Uhr
Der Gödelsche Unvollständigkeitssatz ist einer der wichtigsten Sätze der modernen Logik. Er beschäftigt sich mit der Ableitbarkeit von Aussagen in formalen Systemen. Der Satz zeigt die Grenzen der formalen Systeme ab einer bestimmten Leistungsfähigkeit auf. Er weist nach, dass es in hinreichend starken Systemen, wie der Arithmetik, Aussagen geben muss, die man formal weder beweisen noch widerlegen kann. Der Satz beweist damit die Undurchführbarkeit des Hilbertprogramms, das von David Hilbert unter anderem begründet wurde, um die Widerspruchsfreiheit der Mathematik zu beweisen.[1]
Kurt Gödel
Kurt Gödel war ein Mathematiker des 20.Jahrhunderts, der sich viel mit der Lehre der Logik in der Mathematik beschäftigte. So suchte er auch nach Antworten auf Hilberts Probleme und Fragen. Als Antwort auf das zweite Problem, "Sind die arithmetischen Axiome widerspruchsfrei?", entstanden die Unvollständigkeitssätze Gödels, auf welche im weiteren eingegangen wird.
Gödelsche Unvollständigkeitssätze
Veröffentlicht im Jahr 1931 besagen die Unvollständigkeitssätze als ganzes, dass es in hinreichend starken Systemen (Bsp. Arithmetik) Aussagen geben kann, von denen man weder beweisen kann, dass sie wahr sind, noch diese widerlegen kann. So besagt Gödels erster Unvollständigkeitssatz, dass es in allen widerspruchsfreien Systemen Aussagen gibt, deren Wahrheitsgehalt weder be- noch wiederlegt werden kann. Der zweite Satz besagt, dass man in widerspruchsfreien und hinreichend starken Systemen deren Widerspruchsfreiheit nicht beweisen kann.
Wir legen im folgenden den Fokus auf den ersten Unvollständigkeitssatz. Betrachtet man die Aussage dessen, so stellt sich die Frage: Was mache ich, wenn ich an einer wahren Aussage forsche, aber nicht weiß, ob sie überhapt belegbar ist? Hierzu ein kurzer geschichtlicher Abriss.
Bisheriges Verständnis
Seit dem antiken Griechenland ist man davon ausgegangen, dass alles mathematisch Wahre auch innerhalb der Mathematik bewiesen werden kann. Gödel hat jedoch mit seinen Unvollständigkeitssätzen gezeigt, dass "wahr" und "beweisbar" nicht zwingend zusammenhängen müssen. Ein Beispiel dafür, dass man nicht sagen, oder besser beweisen kann, was wahr und was falsch ist, können wir aus unserem Alltag konstruieren. Betrachtet man ein Blatt Papier und schreibt auf die eine Seite, “Die andere Seite des Papiers ist wahr”, und auf jene angesprochene andere Seite, “Die andere Seite der Papiers ist falsch”, so findet man sich beim Versuch zu ergründen, welche Aussage nun stimmt, in einem Dilemma wieder, da man nicht sagen kann, welche Seite des Papiers nun “Recht” hat. Dies ist für uns im Alltag kein Problem, da wir nicht davon ausgehen, dass alle Aussagen wahr oder falsch sein müssen, oder sogar beweisbar wahr sind. Gödel sagt jedoch, dass ein solches Dilemma auch in der Mathematik auftreten kann - nun wird daraus in der Mathematik tatsächlich ein Problem. Denn wir verlangen von mathematischen Systemen Konsistenz, das heißt, dass jede Aussage entweder wahr oder falsch ist. In anderen Worten sollen mathematische Systeme widerspruchsfrei sein. Gödel hinterfragt also die Vollständigkeit der Mathematik und zeigt letztendlich, dass ausreichend komplexe mathematische Systeme unter Annahme von Konsistenz nicht vollständig sein können.
Wie bereits erwähnt, war dieser Tatbestand der Vollständigkeit der Mathematik eines der Probleme Hilberts: “Prove Math is consistent”. Kurt Gödel hat dieses Problem mit seinem Unvollständigkeitssatz gelöst, oder besser gesagt widerlegt, indem er beweisen hat, dass Mathematik nicht vollständig ist.
Doch genug der Geschichtsstunde, betrachten wir nun, was Gödel eigentlich herausgefunden hat.
Versuchte Erklärung der Beweisidee
Um den Beweis von Gödel zu verstehen, müssen wir zuerst einen kurzen Blick auf die generelle Beweisstruktur der heutigen Mathematik werfen. Die Grundlage der verwendeten Mathematik sind festgelegte Axiome, wie z.B.: "Mengen sind genau dann gleich, wenn sie dieselben Elemente enthalten"[2]. Hat man nun eine mathematische Aussage, so versucht man diese aus den festgelegten Axiomen zu beweisen oder zu widerlegen. Findet man dabei etwas, das immer gültig ist, jedoch nicht bewiesen werden kann, so macht man es zu einem neuen Axiom, einem als wahr angesehenen Grundbaustein der Mathematik. Bisher war man also der Ansicht, dass wenn man nur genügend Axiome hat, alle Aussagen beweisbar sind, oder besser gesagt, irgendwann alle Axiome gefunden sind und alles bewiesen werden kann. Kurzum, man ist davon ausgegangen, dass die Mathematik irgendwann vollständig abgeschlossen ist.
Betrachten wir nun, was Gödel in seinem Beweis macht. Seine Idee war es, die Mathematik in Zahlen umzuformen und dann, durch beispielsweise Primfaktorzerlegung, allen Aussagen Nummern zuzuordnen, die unfehlbar nach Dekodierung auf die Nummern der Axiome zurückführen, und somit die Aussagen beweisen. Als erstes führt er hierfür den sogenannten Gödelcode, oder auch Gödelnumbering ein, womit er jedem Axiom und jeder Aussage, nach einem festgelegten Prinzip eine Nummer, die Gödelnummer, zuordnet. Diese Nummern werden dabei sehr groß, da jede Aussage ihre eigene individuelle Gödelnummer bekommt. Ein Beispiel aus der heutigen technologisierten Welt ist der Ascii-Code, der jedem Buchstaben, Sonderzeichen oder Smiley eine bestimmte vom Computer auslesbare Kombination gibt. Wie auch beim Ascii-Code sorgt eine Zusammensetzung der einzelnen Axiome oder auch Aussagen für eine größere Nummer. So kann beispielsweise ein Smiley durch Kombination mit einer Farbe in unterschiedlichen Gesichtsfarben dargestellt werden. Damit hat Gödel sein Primärziel erreicht. Er kann nun mit Mathematik, als festgelegtes äußeres System Aussagen über die in Gödelnummern festgelegte Mathematik treffen. Vereinfacht gesagt, man kann aus den Nummern bestimmen, ob eine Aussage aus den Axiomsnummern zusammengesetzt werden und damit bewiesen werden kann oder nicht.
Hier lohnt es sich ein kurzes Beispiel anzusehen. In dem System von Gödel das von Nagel und Newman verwendet wird, ist die 0 eine 6 und das Ist-Gleich-Zeichen die 5. Will man also 0=0 in dem System schreiben so findet sich das unter der Nummer 26 * 35 * 56 = 243,000,000.
Kommen wir nun zu einer Aussage, die das ganze problematisch werden lässt und zeigt, dass Mathematik eben doch nicht vollständig ist und es weitergeführt auch niemals sein wird. Diese Aussage lautet: “Diese Aussage kann nicht aus den Axiomen bewiesen werden”. Gehen wir nun als erstes davon aus, dass diese Aussage falsch ist, so muss sie aus den Axiomen beweisbar sein. Dies wäre aber ein Widerspruch, denn wir nehmen an, dass in widerspruchsfreien Systemen nur wahre Aussage bewiesen werden können. Ist dies nicht der Fall, so muss die Aussage, da sie mit Mathematik beschrieben wurde, zwingend richtig sein, da es nach unserem Verständnis in der Mathematik beim rechnen, in diesem Fall mit den Gödelnummern, nur Richtig oder Falsch gibt. Wir haben also in unserem mathematischen System eine Aussage gefunden, die zwar richtig ist, jedoch nicht aus den Axiomen nachgewiesen werden kann. Wichtig hierbei ist, dass wir diese Aussage nur als wahr klassifizieren können, da wir die Mathematik von außerhalb mit sich selbst betrachtet haben. In dem eigentlich betrachteten System, der in den Gödelnummern festgelegten Mathematik, in dem die Aussage “lebt”, kann diese weder widerlegt noch bewiesen werden, obwohl wir von außerhalb wissen, dass sie wahr ist. Wir haben also eine Aussage wahren Inhalts gefunden, die innerhalb eines abgeschlossenen mathematischen Systems nicht bewiesen werden kann. Wir haben bereits erwähnt, dass eine solche Aussage dann als Axiom festgelegt wird. Wenn wir erneut eine solche Aussage finden, dann wird auch diese als Axiom mit aufgenommen, bis es nicht mehr möglich ist eine derartige Aussage zu finden. Nun hat Gödel gezeigt, dass es unendlich viele Aussagen dieses Typus gibt, also die Mathematik niemals vollständig sein kann. Damit wird es immer Aussagen geben die zwar wahr sind, jedoch nicht bewiesen werden können.
Bedeutung für Mathematiker heute
Betrachtet man nun die Auswirkungen von Gödels Unvollständigkeitssätzen auf die heutige Zeit, so fällt auf, dass diese obwohl sie die Mathematik in ihren Grundfesten erschüttert haben, für die eigentliche Forschung an aktuellen Problemen nur bedingte Auswirkung haben. Man kann nicht mehr davon ausgehen für alles eine Lösung zu finden und die Mathematik wird niemals fertig sein. Dies ist auch gut so, denn wenn beispielsweise jeder Mathematiker nach einer Woche sagen würde, "Das Forschungsgebiet taugt nichts, das ist doch wahrscheinlich nicht beweisbar", dann würde die Mathematik als solche keine Fortschritte mehr machen. Somit ändert Gödels Feststellung der unvollständigen Mathematik an der aktuellen Forschung und Problemlösung nur in sofern etwas, dass man immer im Kopf behalten sollte, dass es möglicherweise in letzter Konsequenz doch keinen Beweis der These gibt, und man vielleicht in Betracht ziehen sollte zu überprüfen, ob die These überhaupt beweisbar ist. Auf der anderen Seite hat Gödel jedoch damit ein neues umso unvorhersehbareres Forschungsgebiet eröffnet, welches in der Vergangenheit bereits erstaunliche Ergebnisse geliefert hat.
Neue Beweismethode
Eine Folge Gödels Ergebnisse, welche man vielleicht als etwas seltsam bezeichnen könnte, ist die Möglichkeit zu beweisen, dass etwas innerhalb von einem Axiomsystem nicht widerlegbar oder nicht beweisbar ist. Dies ermöglicht eine neue Beweismethode. Sollte man zum Beispiel beweisen können, dass Die Riemannsche Vermutung innerhalb unseres Axiomsystems nicht entscheidbar ist, würde dies allgemein implizieren, dass die Vermutung wahr sein muss. Denn wäre sie falsch, dann gäbe es sofort eine implementierbare Methode in unserem System, welche ein Gegenbeispiel, d.h. eine nichttriviale Null außer den kritischen Streifen, finden kann.
Beispiele für Gödels Sätze
Nachdem wir nun den Inhalt sowie das Konzept der Unvollständigkeitssätze betrachtet haben, möchten wir abschließend noch den Blick auf zwei Beispiele für das Unvorhersagbare, oder auch Unbeweisbare liefern.
Kontinuumshypothese
Die Frage
Die Kontinuumshypothese wurde 1878 vom Mathematiker Georg Cantor aufgestellt und beinhaltet eine Vermutung über die Mächtigkeit des Kontinuums, also der Menge der reellen Zahlen.
In der einfachen Formulierung besagt die Hypothese, dass es keine Menge gibt, deren Mächtigkeit zwischen der Mächtigkeit der natürlichen Zahlen und der Mächtigkeit der reellen Zahlen liegt.
Lösung aber keine Antwort
Gödel bewies 1938, dass unter der Annahme, dass die Zermelo-Fraenkel-Mengenlehre mit dem Auswahlaxiom (ZFC) widerspruchsfrei ist, auch die Kontinuumshypothese widerspruchsfrei ist. Also, dass man im Rahmen der ZFC die Kontinuumshypothese nicht widerlegen kann. Ungefähr zwanzig Jahre später zeigte Paul Cohen dann das Gegenteil, nämlich dass man mit ZFC die Kontinuumshypothese nicht beweisen kann. Insgesamt war somit die Lösung zu Cantors Fragestellung, dass die Kontinuumshypothese im Rahmen von ZFC nicht lösbar ist. Da sowohl die Kontinuumshypothese und ihre Negation beide ohne Widerspruch ZFC als Axiome erweitern konnten, sind sie eines der ersten relevanten Beispiele für Gödels ersten Unvollständigkeitssatz.
Qual der Wahl
Die Arbeit um die Kontinuumshypothese war damit aber längst nicht fertig. Denn die Frage: "Was ist die genaue Mächtigkeit des Kontinuums?" welche in der Kontinuumshypothese an sich gestellt wurde, blieb immer noch unbeantwortet. Und da ZFC sich als eine nicht ausreichende Liste an Axiomen um diese Frage zu beantworten herausgestellt hat, muss man entscheiden, mit welchen Axiomen ZFC ergänzt werden soll, um die Frage beantworten zu können. Das ist ein gutes Beispiel für die Auswirkungen von Gödels Gesetzten. Nur weil eine Frage innerhalb eines Axiomensystems nicht beantwortet werden kann, muss dies nicht heißen, dass keine Antwort existiert. Dies wird auch deutlich in der Aussage von Menachem Magidor: “The axioms do not settle these problems so we must extend them to a richer axiom system.”[3] Hier fängt aber die Diskussion an, womit das System ergänzt werden soll. Die Suche nach “richtigen” Axiomen stellt sich als besonders schwer dar, denn, wie Gödel bewiesen hat, wird jedes ausreichend komplexe Axiomensystem unvollständig sein. Somit gibt es keine “richtigen” Axiomen und die Auswahl zwischen zwei besonders guten Vorschlägen kann sehr schwer sein. Im Fall der Kontinuumshypothese ist das aktuell ein offenes Problem.
Neuer Fortschritt
Zwei gute Axiome haben sich herausgestellt, das “Martin’s maximum++" und “(*)”. Martin's maximum++ ist eine technische Variation vom Martin's maximum[4] und (*)[5] (ausgesprochen "Star" bzw. "Stern"), ein Axiom welches sich auf eine Mengenlehre bezieht, die neun der Zermelo-Fraenkel Axiome erfüllt zusammen mit dem Axiom der Determiniertheit anstatt des Axioms der Wahl. Jedoch hat man die beiden Axiome bisher als sich gegenseitig ausschließend verstanden. Nun ergaben Forschungsergebnisse von Ralf Schindler und David Asperó einen Grund, um anders zu denken. Die beide Mathematiker behaupten, sie könnten eine Implikation zwischen den beiden Axiomen beweisen. Sollte der Versuch gelingen, würden sich die Aussagen nicht widersprechen und man könnte eine wählen und als Axiom festlegen, ohne die Vorteile der anderen aufgeben zu müssen. Sollte das passieren und das neue Axiom aufgenommen sein, so wäre die Mächtigkeit des Kontinuums als Aleph 2 festgelegt. Auf der anderen Seite arbeitet Hugh Woodin an einer Lösung welche die Mächtigkeit auf Aleph 1 setzen würde. Sein sogenanntes “Ultimate L” Modell sollte eine Verallgemeinerung von Gödels Mengenlehre sein.
Game of Life
Grundlagen
Ein weiteres Beispiel ist das “Game of Life” von John Horton Conway. Bei diesem "Kein Spieler Spiel", gibt es ein unendliches, in quadratische Felder eingeteiltes Spielbrett, auf welchem zu Beginn beliebig Spielsteine platziert werden können. Dann wird das Spiel oder die “Simulation” gestartet. Jede Runde entstehen oder verschwinden Spielsteine. Hierbei wird ein Feld, auf welchem ein Spielstein liegt, als lebend und ein Feld ohne Spielstein als tot bezeichnet. Außerdem hat jedes Feld 8 Nachbarn. Nun verändert sich das Spielfeld, bzw. die Verteilung der Stein zu Beginn jeder Runde nach folgenden Regeln, die simultan für alle Felder ausgeführt werden:
- Eine totes Feld mit genau drei lebenden Nachbarn wird in der folgenden Runde neu “geboren”, also mit einem Spielstein besetzt.
- Lebende Felder mit weniger als zwei lebenden Nachbarn sterben in der folgenden Runde an Einsamkeit, also wird der Spielstein entfernt.
- Ein lebendiges Feld mit zwei oder drei lebenden Nachbarfeldern bleibt in der Folgegeneration am Leben. Es passiert also nichts mit dem Feld.
- Lebende Felder mit mehr als drei lebenden Nachbarfeldern sterben in der Folgegeneration an Überbevölkerung, also wird der Spielstein entfernt.
- Tote Felder ohne Nachbarn bleiben tot.
Jede Runde ist im übertragenen Sinne eine Generation. Nun wird das Spiel gestartet und das Spielfeld verändert sich in jeder Runde. Hierbei können aus unterschiedlichen Anfangskonstellationen unterschiedliche Formationen entstehen. Dabei gibt es prinzipiell drei mögliche Ausgänge der Simulation.
- Es entstehen konstante Konstellationen, die nach einer gewissen Anzahl wieder in einer bereits durchlaufenen Konstellation auftauchen. Diese können statisch sein, oder sich über das Feld bewegen.
- Es werden immer mehr Felder besetzt.
- Es sterben immer mehr Zellen, bis das Spielfeld letztlich leer/tot ist.
Beispiele:
Konstante Konstellationen:
- Statische:
- Statische Konstellationen
- Oszillierende:
- Wandernde/Raumschiffe:
Erzeugende Konstellationen
- Gleiterkanone:
Sterbende Konstellationen
Verschiedene Möglichkeiten, Beispiel: einzelnes Feld
Das Unvorhersagbare an diesem Beispiel ist, dass man aus der Anfangskonstellation nicht vorhersagen kann was passieren wird, ausgenommen bei bereits bekannten Konstellationen. Um also herauszufinden was mit einer bestimmten Konstellation passiert, muss man diese solange laufen lassen, bis man eine statische oder oszillierende, eine nach festem Prinzip wachsende, oder eine nicht mehr existente Konstellation gefunden hat. Hierbei lässt sich nicht sagen: "Diese Konstellation hat jetzt 100 Generationen überlebt, deshalb überlebt sie für immer". So kann eine riesige Konstellation, die nach einer Million Lebenszyklen noch lebt, nach beispielsweise einer weiteren Million Generationen vollständig verschwunden sein.
Hierfür ein Beispiel, das auch der Intuition widerspricht, ist das r-Pentomino, welches am Anfang ein chaotisch wachsendes Muster aufweist und nach 1103 Generationen dann ein fast vollständig statisch oder oszillierendes Spielfeld hinterlässt. Ausnahme sind wenige wegfliegende Gleiter.
Wer möchte kann es hier selbst versuchen: Game of Life spielen
Was das Game of Life kann
Man hat inzwischen festgestellt, dass es möglich ist, in Conways Game of Life, Schaltungen wie "und" und "oder" zu bauen, und es sogar gelungen ist, das Game of Life im Game of Life zu bauen, was bedeutet, dass das Game of Life "Turing complete" ist. Dies geht nun aber tatsächlich weit über das eigentliche Thema der Unvollständigkeitssätze hinaus. Deshalb wollen wir das Thema hier nicht weiter ausführen.
Quellen
Externe Quellen
Autoren
Kaspar Haas
Leon-Josip Dzojic
- ↑ https://de.wikipedia.org/wiki/G%C3%B6delscher_Unvollst%C3%A4ndigkeitssatz
- ↑ https://de.wikipedia.org/wiki/Zermelo-Fraenkel-Mengenlehre#:~:text=1.%20Extensionalit%C3%A4tsaxiom%3A%20Mengen%20sind%20genau%20dann%20gleich%2C%20wenn%20sie%20dieselben%20Elemente%20enthalten.
- ↑ https://www.quantamagazine.org/how-many-numbers-exist-infinity-proof-moves-math-closer-to-an-answer-20210715/#:~:text=The%20axioms%20do%20not%20settle%20these%20problems%2C%E2%80%9D%20said%20Magidor%2C%20so%20%E2%80%9Cwe%20must%20extend%20them%20to%20a%20richer%20axiom%20system.%E2%80%9D%20It%E2%80%99s%20ZFC%20as%20a%20means%20to%20mathematical%20truth%20that%E2%80%99s%20lacking%20%E2%80%94%20not%20truth%20itself.
- ↑ https://www.quantamagazine.org/how-many-numbers-exist-infinity-proof-moves-math-closer-to-an-answer-20210715/#:~:text=In%201988%2C%20Magidor%2C%20Matthew%20Foreman%20and%20Saharon%20Shelah%20took%20this%20ethos%20to%20its%20logical%20conclusion%20by%20posing%20Martin%E2%80%99s%20maximum%2C%20which%20says%20that%20anything%20you%20can%20conceive%20of%20using%20any%20forcing%20procedure%20will%20be%20a%20true%20mathematical%20entity%2C%20so%20long%20as%20the%20procedure%20satisfies%20a%20certain%20consistency%20condition.
- ↑ https://www.quantamagazine.org/how-many-numbers-exist-infinity-proof-moves-math-closer-to-an-answer-20210715/#:~:text=Woodin%20proposed%20another,axiom%20of%20choice.