Normen und Metriken: Unterschied zwischen den Versionen
ArianG (Diskussion | Beiträge) |
|||
| (103 dazwischenliegende Versionen von 3 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | Eine '''Norm''' ist eine Abbildung, die auf einem Vektorraum definiert ist und jedem Objekt in diesem Vektorraum eine reelle Zahl zuordnet, die die Größe des Objekts beschreiben soll. Eine '''Metrik''' ist auf einer Menge definiert und ordnet je zwei Punkten eine reelle Zahl zu, die gewissermaßen den Abstand der Punkte | + | Eine '''Norm''' ist eine Abbildung, die auf einem Vektorraum definiert ist und jedem Objekt in diesem Vektorraum eine reelle Zahl zuordnet, die die Größe des Objekts beschreiben soll. Eine '''Metrik''' ist auf einer Menge definiert und ordnet je zwei Punkten eine reelle Zahl zu, die gewissermaßen den Abstand der Punkte angibt. |
| − | '''Normen und Metriken''' sind nicht eindeutig auf dem Vektorraum | + | '''Normen und Metriken''' sind nicht eindeutig auf dem Vektorraum beziehungsweise der Menge definiert und so ist es durchaus möglich, dass beispielsweise unterschiedliche Normen dem gleichen Objekt eine andere Größe zuordnen. Dennoch erfüllen Normen und Metriken drei definierende Eigenschaften, und grundlegende Konzepte wie beispielsweise Konvergenz sind unabhängig von der gewählten Norm beziehungsweise Metrik. |
== Motivation == | == Motivation == | ||
| − | Unser Ziel ist es | + | Unser Ziel ist es Objekten in einem Raum eine gewisse Größe und einen gewissen Abstand zuzuordnen. Aus den reellen Zahlen kennen wir bereits den Absolutbetrag und die absolute Differenz. Dieses Konzept möchten wir abstrahieren und so allgemein wie möglich formulieren, sprich auch einen Abstands- und Größenbegriff für Vektorräume oder idealerweise allgemeine Mengen definieren. Den Größenbegriff werden wir dann als Norm bezeichnen, den Abstandsbegriff als Metrik. |
| − | Wir werden feststellen, dass wir Normen auf vielen Vektorräumen definieren können und somit einen Größenbegriff für | + | Wir werden feststellen, dass wir Normen auf vielen Vektorräumen definieren können und somit einen Größenbegriff, beispielsweise für Vektoren und Matrizen, aber auch für weniger intuitive Dinge wie Funktionen, erhalten. Metriken können wir sogar auf allgemeinen Mengen definieren, ohne eine Vektorraumstruktur zu benötigen. |
== Norm == | == Norm == | ||
| Zeile 40: | Zeile 40: | ||
=== Äquivalenz von Normen === | === Äquivalenz von Normen === | ||
| − | Zwei Normen sind äquivalent, wenn eine Norm durch die andere nach oben und unten abgeschätzt werden kann, | + | Zwei Normen <math>\|\cdot\|_a </math> und <math>\|\cdot\|_b </math> sind äquivalent, wenn eine Norm durch die andere nach oben und unten abgeschätzt werden kann, das heißt: |
| − | es gibt | + | es gibt zwei positive Konstanten <math>c_1</math> und <math>c_2</math>, sodass für alle <math>x \in V</math> folgendes gilt: |
: <math>c_1 \|x\|_b\leq \|x\|_a\leq c_2 \|x\|_b</math> | : <math>c_1 \|x\|_b\leq \|x\|_a\leq c_2 \|x\|_b</math> | ||
| + | In endlichdimensionalen Vektorräumen gilt, dass alle Normen äquivalent sind. Somit ist der Konvergenzbegriff in endlichdimensionalen Vektorräumen unabhängig von der gewählten Norm. Andere Konzepte müsssen nicht unabhängig von der Norm sein, so ist beispielsweise eine Kontraktion bezüglich einer Norm nicht zwingend eine Kontraktion unter einer anderen. | ||
== Metrik == | == Metrik == | ||
=== Definition === | === Definition === | ||
| − | Sei <math>X</math> eine Menge. Eine Abbildung <math>d\colon X\times X\to \mathbb{R}</math> heißt Metrik auf <math>X</math>, falls folgenden Eigenschaften für beliebige <math>x</math>, <math>y</math> und <math>z</math> | + | Sei <math>X</math> eine Menge. Eine Abbildung <math>d\colon X\times X\to \mathbb{R}</math> heißt Metrik auf <math>X</math>, falls folgenden Eigenschaften für beliebige <math>x</math>, <math>y</math> und <math>z</math> aus <math>X</math> gelten: |
{| | {| | ||
| − | | '''M1''' Positive Definitheit: | + | | style="width:20em;" |'''M1''' Positive Definitheit: || <math>d\left(x,y\right) \geq 0</math> und <math>d\left(x,y\right) = 0 \Leftrightarrow x = y</math>, |
|- | |- | ||
| − | | '''M2''' Symmetrie: || <math>d\left(x,y\right) = d(y,x)</math>, | + | | |'''M2''' Symmetrie: || <math>d\left(x,y\right) = d(y,x)</math>, |
|- | |- | ||
| − | | '''M3''' Dreiecksungleichung: || <math>d\left(x,y\right) \leq d(x,z) + d(z,y)</math>. | + | | |'''M3''' Dreiecksungleichung: || <math>d\left(x,y\right) \leq d(x,z) + d(z,y)</math>. |
|} | |} | ||
| − | + | Das Paar (<math>X</math>,d) nennt man '''metrischer Raum'''. | |
| + | |||
===Bemerkung=== | ===Bemerkung=== | ||
| − | Für eine Metrik <math>d</math> | + | Für eine Metrik <math>d</math> kann folgende Bedingung auch weggelassen werden: |
<math>d(x,y)\geq0</math> | <math>d(x,y)\geq0</math> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Da aus [[#Metrik|M1]] (2. Teil), [[#Metrik|M2]] und [[#Metrik|M3]] folgendes gilt: | ||
: <math>0 = \frac{1}{2} d(x, x) \leq \frac{1}{2}(d(x, y) + d(y, x)) = \frac{1}{2}(d(x, y) + d(x, y)) = d(x, y).</math> | : <math>0 = \frac{1}{2} d(x, x) \leq \frac{1}{2}(d(x, y) + d(y, x)) = \frac{1}{2}(d(x, y) + d(x, y)) = d(x, y).</math> | ||
| − | + | {| | |
| − | |||
|} | |} | ||
| Zeile 75: | Zeile 73: | ||
==Zusammenhang von Norm und Metrik == | ==Zusammenhang von Norm und Metrik == | ||
| − | In den reellen Zahlen wird bekanntermaßen der Absolutbetrag einer Zahl als Abstand der Zahl | + | In den reellen Zahlen wird bekanntermaßen der Absolutbetrag einer Zahl als Abstand der Zahl zur 0 definiert, sprich: |
:<math> |x| = \begin{cases} x & \text{falls}\ x \geq 0 \\ -x & \text{falls}\ x < 0 \end{cases}\ , \ x \in \mathbb{R} </math>, | :<math> |x| = \begin{cases} x & \text{falls}\ x \geq 0 \\ -x & \text{falls}\ x < 0 \end{cases}\ , \ x \in \mathbb{R} </math>, | ||
| − | + | Die absolute Differenz ist definiert als: | |
:<math> d(x,y) = |x-y| , \ \ x,y \in \mathbb{R} </math>. | :<math> d(x,y) = |x-y| , \ \ x,y \in \mathbb{R} </math>. | ||
| − | Dass der Absolutbetrag somit auch in der Definition unseres Abstandes in den reellen Zahlen vorkommt, legt bereits nahe, dass Normen und Metriken nicht zwei zusammenhangslose Konzepte sind, sondern | + | Dass der Absolutbetrag somit auch in der Definition unseres Abstandes in den reellen Zahlen vorkommt, legt bereits nahe, dass Normen und Metriken nicht zwei zusammenhangslose Konzepte sind, sondern dass es eine Verbindung zwischen ihnen gibt und tatsächlich werden wir sehen, dass sehr viele Metriken durch zugrundeliegende Normen definiert werden können ("von Normen induziert werden"). |
=== Induzierte Metriken === | === Induzierte Metriken === | ||
| Zeile 92: | Zeile 90: | ||
'''M3''' <math> d(x,z) = \left\Vert x - z \right\Vert = \left\Vert x - y + y - z \right\Vert \le \left\Vert x - y \right\Vert + \left\Vert y - z \right\Vert = d(x,y)+d(y,z) </math> | '''M3''' <math> d(x,z) = \left\Vert x - z \right\Vert = \left\Vert x - y + y - z \right\Vert \le \left\Vert x - y \right\Vert + \left\Vert y - z \right\Vert = d(x,y)+d(y,z) </math> | ||
| − | Somit besitzt jeder normierte Vektorraum auch eine Metrik, ist also auch ein | + | Somit besitzt jeder normierte Vektorraum auch eine Metrik, ist also auch ein metrischer Raum. |
| − | Im Gegensatz dazu, ist nicht jeder | + | Im Gegensatz dazu, ist nicht jeder metrische Vektorraum auch ein normierter Vektorraum, [https://funfacts.mathi.uni-heidelberg.de/index.php/Normen_und_Metriken#Nicht_durch_Normen_induzierte_Metriken s. Beispiele] |
== Hierarchie Topologischer Räume == | == Hierarchie Topologischer Räume == | ||
| − | [[Datei:1200px-Beziehungen zwischen mathematischen Räumen.svg.png|mini| | + | [[Datei:1200px-Beziehungen zwischen mathematischen Räumen.svg.png|mini|253x253px|Hierarchie topologischer Räume]] |
| − | Wie gesehen, | + | Wie gesehen, induziert jede Norm eine Metrik, somit ist jeder normierte Vektorraum auch ein metrischer Raum. Analog dazu induziert jedes Skalarprodukt <math> (\cdot,\cdot) </math> eine Norm via <math> \left\Vert v \right\Vert = \sqrt{(v.v)} </math>. |
Außerdem induziert jede Metrik auf dem metrischen Raum <math> (M,d) </math> eine Topologie via <math> \ \mathcal{O} := \{U \subset M, U\ \text{ist offen bzgl.}\ d\}. </math> | Außerdem induziert jede Metrik auf dem metrischen Raum <math> (M,d) </math> eine Topologie via <math> \ \mathcal{O} := \{U \subset M, U\ \text{ist offen bzgl.}\ d\}. </math> | ||
| − | Somit erhält man die folgende Hierarchie | + | Somit erhält man die folgende Hierarchie von Räumen: |
== Metrik Beispiele == | == Metrik Beispiele == | ||
=== Durch Normen induzierte Metriken === | === Durch Normen induzierte Metriken === | ||
Jede Norm die es auf einem Vektorraum gibt induziert wie folgt eine Metrik | Jede Norm die es auf einem Vektorraum gibt induziert wie folgt eine Metrik | ||
| − | :<math>d(x, y) | + | :<math>d(x, y) := \|x - y\|</math> |
| − | Daher sehen wir, dass jeder normierte | + | Daher sehen wir, dass jeder normierte Vektorraum ein metrischer Raum ist. |
:Ein weiteres Beispiel ist: | :Ein weiteres Beispiel ist: | ||
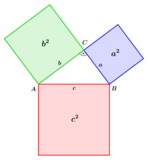
[[Datei:Satz des Pythagoras.svg.png|mini|160x160px|Satz des Pythagoras]] | [[Datei:Satz des Pythagoras.svg.png|mini|160x160px|Satz des Pythagoras]] | ||
| − | + | === Die euklidische Metrik === | |
In der zweidimensionalen euklidischen Ebene stimmt der euklidische Abstand <math>d(x,y)</math> mit dem gängigen Gedanken des Abstandes überein. | In der zweidimensionalen euklidischen Ebene stimmt der euklidische Abstand <math>d(x,y)</math> mit dem gängigen Gedanken des Abstandes überein. | ||
| Zeile 117: | Zeile 115: | ||
: <math>d(x,y) = \|x-y\|_2 =\sqrt{(x_1 - y_1)^2 + \cdots + (x_n - y_n)^2} = \sqrt{\sum_{i=1}^n (x_i-y_i)^2}</math> | : <math>d(x,y) = \|x-y\|_2 =\sqrt{(x_1 - y_1)^2 + \cdots + (x_n - y_n)^2} = \sqrt{\sum_{i=1}^n (x_i-y_i)^2}</math> | ||
| − | + | Der Satz des Phytagoras stellte eine Formel für den Abstandsbegriff in dem kartesischen Koordinatensystem, beispielsweise im n=2 kann man sich die Berechnung des Abstandes wie ein Rechtwinkliges Dreieck vorstellen, durch: <math>c = \sqrt{(x_1-x_0)^2 + (y_1-y_0)^2}</math> wobei <math>c</math> den Abstand zwischen den Punkten <math>(x_0,y_0), (x_1,y_1)</math> darstellt. Im Bild rechts könnte man sich die Strecken <math>x_1-x_0</math> und <math>y_1-y_0</math> als a und b vorstellen und den berechneten Abstand <math>c</math> als c. | |
| − | Der euklidische Abstand ist eine | + | Der euklidische Abstand ist eine Metrik welche die Dreiecksungleichung erfüllt. Die Axiome einer Norm werden ebenfalls erfüllt, somit wird es folglich durch eine Norm induziert, welche man auch die euklidische Norm nennt. |
=== Nicht durch Normen induzierte Metriken === | === Nicht durch Normen induzierte Metriken === | ||
| − | Es gibt Metriken welche | + | Es gibt Metriken welche die Axiome [[#Norm|N1-N3]] einer Norm nicht erfüllen ein Beispiel hierfür ist folgende Metrik welche das Axiom [[#Norm|N2]] nicht erfüllt: |
| − | + | ||
| − | Auf jeder | + | ===Die Diskrete Metrik=== |
| − | + | Auf jeder Menge lässt sich die triviale Metrik definieren. Sie wird auch diskrete Metrik gennant und ist dazu noch eine [[#Ultrametrik|Ultrametrik]]. | |
| + | Sie wird wie folgt definiert: | ||
:Sei <math>X</math> eine Menge, <math>x</math>,<math>y</math> aus <math>X</math> und <math>d</math> eine Abbildung <math> d\colon X\times X\to\mathbb R </math> mit | :Sei <math>X</math> eine Menge, <math>x</math>,<math>y</math> aus <math>X</math> und <math>d</math> eine Abbildung <math> d\colon X\times X\to\mathbb R </math> mit | ||
:<math>d(x,y)=\begin{cases} | :<math>d(x,y)=\begin{cases} | ||
| Zeile 132: | Zeile 131: | ||
Diese Metrik induziert die diskrete Topologie. | Diese Metrik induziert die diskrete Topologie. | ||
| − | Ein weiteres Beispiel, | + | Die diskrete Metrik wird nicht durch eine Norm induziert, denn |
| − | + | betrachtet man den Punkt [[#Norm|N2]] einer Norm so sieht man: | |
| + | |||
| + | Sei <math>\| x \|=d(x,0)</math> und sei <math>x</math> ungleich 0 so ist, | ||
| + | |||
| + | <math>\| 2x \|=d(2x,0)=1≠2=2d(x,0)=|2|\| x \|</math> | ||
| + | |||
| + | Also kann die diskrete Metrik nicht durch eine Norm induziert werden. | ||
| + | |||
| + | |||
| + | Ein weiteres Beispiel, welches nicht alle Axiome einer Norm erfüllt, ist die: | ||
| + | |||
| + | ===Die SNCF-Metrik=== | ||
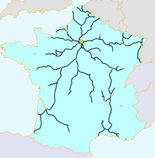
[[Datei:French railway network 1856.png|mini|alternativtext=|158x158px|Französisches Bahnnetz 1856]] | [[Datei:French railway network 1856.png|mini|alternativtext=|158x158px|Französisches Bahnnetz 1856]] | ||
Sei <math>X</math> eine Menge von Punkten in der Ebene und <math> p </math> ein fester Punkt. | Sei <math>X</math> eine Menge von Punkten in der Ebene und <math> p </math> ein fester Punkt. | ||
| Zeile 149: | Zeile 159: | ||
Der Name dieser Metrik leitet sich von der Eisenbahngesellschaft SNCF ab, da diese Metrik in den Kontext des Französischen Eisenbahnnetzes fällt. | Der Name dieser Metrik leitet sich von der Eisenbahngesellschaft SNCF ab, da diese Metrik in den Kontext des Französischen Eisenbahnnetzes fällt. | ||
Nehme man an X seien die Städte Frankreichs, und <math> p </math> Paris so kann der Abstand, falls es keinen direkt Zug zwischen der Stadt <math>x</math> und <math>y</math> gibt, deutlich länger werden. | Nehme man an X seien die Städte Frankreichs, und <math> p </math> Paris so kann der Abstand, falls es keinen direkt Zug zwischen der Stadt <math>x</math> und <math>y</math> gibt, deutlich länger werden. | ||
| + | |||
| + | |||
| + | Die SNCF-Metrik wird nicht von einer Norm induziert, denn wäre dem so, würde diese Norm die folgende Gleichung erfüllen: | ||
| + | : <math> \| x \| = d(x,0) </math>. | ||
| + | |||
| + | Es ist jedoch, falls <math> p </math> nicht auf einer Geraden durch <math> 0 </math> und <math> x </math> liegt (und damit auch nicht <math> 0 </math> ist) | ||
| + | : <math> d(x,0) = \| x-p \| + \| p \| \neq \| x \| </math>. | ||
| + | Deshalb gibt es keine Norm, die die SNCF-Metrik induziert. | ||
== Spezielle Metriken == | == Spezielle Metriken == | ||
=== Ultrametrik === | === Ultrametrik === | ||
| − | Eine Metrik nennt man Ultrametrik falls bei der | + | Eine Metrik nennt man Ultrametrik falls bei der [[#Metrik|M3]] Dreiecksungleichung gilt, dass der Abstand <math>d(x, y)</math> nicht länger ist als der längere der beiden Abstände <math>d(x, z)</math> und <math>d(z, y)</math> und das mit beliebigem <math>z</math>. Beispielsweise ist die diskrete Metrik eine Ultrametrik. |
=== Pseudometrik === | === Pseudometrik === | ||
| − | + | Eine Pseudometrik ist eine Metrik in welcher die Bedingung aus [[#Metrik|M1]] <math>d\left(x,y\right) = 0 \Rightarrow x = y</math> nicht gilt, somit ist sie positiv semidefinit. Sie wird in der Funtkionalanalysis auch als Halb- oder Semimetrik bezeichnet. | |
=== Nicht-archimedische Metriken === | === Nicht-archimedische Metriken === | ||
| − | Hier wird die | + | Hier wird die [[#Metrik|M3]] Dreiecksungleichung verstärkt oder geschwächt. Ein Beispiel für diese Metrik wäre die Ultrametrik. |
=== Quasimetrik === | === Quasimetrik === | ||
| − | Verzichtet man auf | + | Verzichtet man auf [[#Metrik|M2]] (Symmetrie) der Axiome so erhält man eine Quasimetrik. Eine Quasimetrik <math>b</math> erzeugt durch <math>d(x,y):= \tfrac{1}{2} ( b(x,y) + b(y,x) )</math> eine Metrik auf <math>X</math>. |
=== Prämetrik === | === Prämetrik === | ||
| − | Die Prämetrik fordert nur das Axiom | + | Die Prämetrik fordert nur das Axiom [[#Metrik|M1]] (Positive Definitheit). |
== Norm Beispiele == | == Norm Beispiele == | ||
| Zeile 201: | Zeile 219: | ||
: <math>\| x \|_1 = \sum_{i=1}^n | x_i |</math> | : <math>\| x \|_1 = \sum_{i=1}^n | x_i |</math> | ||
| − | ==== | + | ==== p-Normen ==== |
| + | [[Datei:P Norm-1.jpg|mini|Beweis N3]] | ||
| + | Man kann für jedes reelles <math>1 \leq p < \infty</math> die <math>p</math>-Norm eines Vektors, durch | ||
| + | |||
| + | : <math>\| x \|_p = \left(\sum_{i=1}^n | x_i |^p\right)^{1/p}</math>, definieren | ||
| + | |||
| + | Wählt man <math>p=1</math> erhält man so die Summennorm, für <math>p=2</math> die euklidische Norm und für <math>p\to\infty</math> die Maximumsnorm. | ||
| + | |||
| + | {| class="wikitable left mw-collapsible mw-collapsed font-size: 100%;" | ||
| + | | style="text-align:left; font-size: 100%;" | '''Beweis''' | ||
| + | |- | ||
| + | | zu zeigen: Die p-Norm ist eine Norm | ||
| + | '''N1''' | ||
| + | : <math>\| x \|_p = 0 \; \Leftrightarrow \; \left(\sum_{i=1}^n | x_i |^p\right)^{1/p} \!\!\!\!\! = 0 \; \Rightarrow \; \sum_{i=1}^n | x_i |^p = 0 \; \Rightarrow \; x = 0</math> | ||
| + | '''N2''' | ||
| + | : <math>\| \alpha \, x \|_p = \left( \sum_{i=1}^n | \alpha \, x_i |^p \right)^{1/p} \!\!\!\!\! = \left( \sum_{i=1}^n | \alpha |^p \, | x_i |^p \right)^{1/p} \!\!\!\!\! = | \alpha | \, \left( \sum_{i=1}^n | x_i |^p \right)^{1/p} \!\!\!\!\! = | \alpha | \, \| x \|_p</math> | ||
| + | '''N3''' | ||
| + | siehe Bild rechts | ||
| + | |} | ||
=== Normen auf unendlichdimensionalen Vektorräumen === | === Normen auf unendlichdimensionalen Vektorräumen === | ||
| − | === Operatornorm === | + | ==== Supremumsnorm ==== |
| + | Die Supremumsnorm einer beschränkten Funktion ist definiert als | ||
| + | |||
| + | : <math>\ \| f \|_{\sup} = \| f \|_{\infty} = \sup_{x \in \Omega} | f(x) |</math>. | ||
| + | |||
| + | ==== Operatornorm ==== | ||
Seien V und W Vektorräume und sei <math>f\colon V \rightarrow W</math> eine lineare Abbildung. Dann ist die Operatornorm definiert als: | Seien V und W Vektorräume und sei <math>f\colon V \rightarrow W</math> eine lineare Abbildung. Dann ist die Operatornorm definiert als: | ||
| Zeile 215: | Zeile 256: | ||
== Quellen == | == Quellen == | ||
{| style="margin-left: 2em" | {| style="margin-left: 2em" | ||
| + | | | https://mampf.mathi.uni-heidelberg.de/mediaforward/medium/27133/manuscript/fd7cf1a2d8b9bc5e9308ef865851e377.pdf/Analysis2-Skript-gesamt.pdf | ||
|- | |- | ||
| − | | https://mampf.mathi.uni-heidelberg.de/mediaforward/medium/27208/manuscript/adf9e7b00ee4803a0e865168bab3fe67.pdf/Metriken_Normen%20.pdf#page=2 | + | | | https://mampf.mathi.uni-heidelberg.de/mediaforward/medium/27208/manuscript/adf9e7b00ee4803a0e865168bab3fe67.pdf/Metriken_Normen%20.pdf#page=2 |
|- | |- | ||
| | https://de.wikipedia.org/wiki/Französische_Eisenbahnmetrik | | | https://de.wikipedia.org/wiki/Französische_Eisenbahnmetrik | ||
| Zeile 225: | Zeile 267: | ||
|- | |- | ||
| | https://de.wikipedia.org/wiki/Norm_(Mathematik) | | | https://de.wikipedia.org/wiki/Norm_(Mathematik) | ||
| + | |- | ||
| + | | | http://kulla.me/de/artikel/zusammenfassung_topologie/ | ||
| + | |- | ||
| + | | | https://mampf.mathi.uni-heidelberg.de/mediaforward/medium/26788/manuscript/12bc7adbe55f813bc35d48c3e4ea7b5f.pdf/Analysis2-Video1-Metrische-Räume-Konvergenz-doppelseitig.pdf | ||
|} | |} | ||
== Autoren == | == Autoren == | ||
Arian Gjini, Alassane Diagne, Robin Klotzbücher | Arian Gjini, Alassane Diagne, Robin Klotzbücher | ||
Aktuelle Version vom 8. Oktober 2021, 19:11 Uhr
Eine Norm ist eine Abbildung, die auf einem Vektorraum definiert ist und jedem Objekt in diesem Vektorraum eine reelle Zahl zuordnet, die die Größe des Objekts beschreiben soll. Eine Metrik ist auf einer Menge definiert und ordnet je zwei Punkten eine reelle Zahl zu, die gewissermaßen den Abstand der Punkte angibt.
Normen und Metriken sind nicht eindeutig auf dem Vektorraum beziehungsweise der Menge definiert und so ist es durchaus möglich, dass beispielsweise unterschiedliche Normen dem gleichen Objekt eine andere Größe zuordnen. Dennoch erfüllen Normen und Metriken drei definierende Eigenschaften, und grundlegende Konzepte wie beispielsweise Konvergenz sind unabhängig von der gewählten Norm beziehungsweise Metrik.
Motivation
Unser Ziel ist es Objekten in einem Raum eine gewisse Größe und einen gewissen Abstand zuzuordnen. Aus den reellen Zahlen kennen wir bereits den Absolutbetrag und die absolute Differenz. Dieses Konzept möchten wir abstrahieren und so allgemein wie möglich formulieren, sprich auch einen Abstands- und Größenbegriff für Vektorräume oder idealerweise allgemeine Mengen definieren. Den Größenbegriff werden wir dann als Norm bezeichnen, den Abstandsbegriff als Metrik.
Wir werden feststellen, dass wir Normen auf vielen Vektorräumen definieren können und somit einen Größenbegriff, beispielsweise für Vektoren und Matrizen, aber auch für weniger intuitive Dinge wie Funktionen, erhalten. Metriken können wir sogar auf allgemeinen Mengen definieren, ohne eine Vektorraumstruktur zu benötigen.
Norm
Definition
Eine Norm ist eine Abbildung [math]\|\cdot\|[/math] von einem Vektorraum [math]V[/math] über dem Körper [math]\mathbb K[/math] der reellen oder komplexen Zahlen in die Menge der nichtnegativen reellen Zahlen [math]{\mathbb R}_0^{+}[/math],
- [math]\|\cdot\|\colon V\to{\mathbb R}_0^{+}, \; x \mapsto \| x \|[/math],
welche die folgenden Axiome für alle Vektoren [math]x, y\in V[/math] und alle Skalare [math]\alpha\in\mathbb K[/math] erfüllt:
| N1 Definitheit: | [math]\|x\| = 0 \;\Rightarrow\; x = 0[/math], |
| N2 Homogenität: | [math]\|\alpha\cdot x\| = |\alpha|\cdot\|x\|[/math], |
| N3 Dreiecksungleichung: | [math]\|x + y\| \leq \|x\| + \|y\|[/math]. |
Grundlegende Eigenschaften
Aus der Homogenität folgt:
- [math]x = 0 \;\Rightarrow\; \| x \| = 0[/math]
Zusammen mit der Definitheit gilt also, dass ein Vektor genau dann die Norm Null hat, wenn er der Nullvektor ist.
Die Symmetrie bezüglich Vorzeichen folgt ebenfalls aus der Definitheit durch Einsetzen von [math]\alpha = -1[/math]:
- [math]\| {-x} \| = \| x \|[/math] und damit [math]\| x-y \| = \| y-x \|[/math]
Mithilfe der der Dreiecksungleichung folgt dann: Setze [math]y = -x[/math],
[math]0= \|x + (-x)\| \leq \|x\| + \|-x\| = 2\| x \| \;\Rightarrow\; \| x \| \geq 0 [/math], also eine Norm ist immer nichtnegativ
Äquivalenz von Normen
Zwei Normen [math]\|\cdot\|_a [/math] und [math]\|\cdot\|_b [/math] sind äquivalent, wenn eine Norm durch die andere nach oben und unten abgeschätzt werden kann, das heißt:
es gibt zwei positive Konstanten [math]c_1[/math] und [math]c_2[/math], sodass für alle [math]x \in V[/math] folgendes gilt:
- [math]c_1 \|x\|_b\leq \|x\|_a\leq c_2 \|x\|_b[/math]
In endlichdimensionalen Vektorräumen gilt, dass alle Normen äquivalent sind. Somit ist der Konvergenzbegriff in endlichdimensionalen Vektorräumen unabhängig von der gewählten Norm. Andere Konzepte müsssen nicht unabhängig von der Norm sein, so ist beispielsweise eine Kontraktion bezüglich einer Norm nicht zwingend eine Kontraktion unter einer anderen.
Metrik
Definition
Sei [math]X[/math] eine Menge. Eine Abbildung [math]d\colon X\times X\to \mathbb{R}[/math] heißt Metrik auf [math]X[/math], falls folgenden Eigenschaften für beliebige [math]x[/math], [math]y[/math] und [math]z[/math] aus [math]X[/math] gelten:
| M1 Positive Definitheit: | [math]d\left(x,y\right) \geq 0[/math] und [math]d\left(x,y\right) = 0 \Leftrightarrow x = y[/math], |
| M2 Symmetrie: | [math]d\left(x,y\right) = d(y,x)[/math], |
| M3 Dreiecksungleichung: | [math]d\left(x,y\right) \leq d(x,z) + d(z,y)[/math]. |
Das Paar ([math]X[/math],d) nennt man metrischer Raum.
Bemerkung
Für eine Metrik [math]d[/math] kann folgende Bedingung auch weggelassen werden:
[math]d(x,y)\geq0[/math]
Da aus M1 (2. Teil), M2 und M3 folgendes gilt:
- [math]0 = \frac{1}{2} d(x, x) \leq \frac{1}{2}(d(x, y) + d(y, x)) = \frac{1}{2}(d(x, y) + d(x, y)) = d(x, y).[/math]
Zusammenhang von Norm und Metrik
In den reellen Zahlen wird bekanntermaßen der Absolutbetrag einer Zahl als Abstand der Zahl zur 0 definiert, sprich:
- [math] |x| = \begin{cases} x & \text{falls}\ x \geq 0 \\ -x & \text{falls}\ x \lt 0 \end{cases}\ , \ x \in \mathbb{R} [/math],
Die absolute Differenz ist definiert als:
- [math] d(x,y) = |x-y| , \ \ x,y \in \mathbb{R} [/math].
Dass der Absolutbetrag somit auch in der Definition unseres Abstandes in den reellen Zahlen vorkommt, legt bereits nahe, dass Normen und Metriken nicht zwei zusammenhangslose Konzepte sind, sondern dass es eine Verbindung zwischen ihnen gibt und tatsächlich werden wir sehen, dass sehr viele Metriken durch zugrundeliegende Normen definiert werden können ("von Normen induziert werden").
Induzierte Metriken
Es sei [math] \left\Vert \cdot \right\Vert [/math] eine Norm auf einem Vektorraum. Dann definiert [math] d(x, y) := \left\Vert x - y \right\Vert [/math] eine Metrik.
Beweis
M1 [math] d(x,y) = 0 \Leftrightarrow \left\Vert x - y \right\Vert = 0 \Leftrightarrow x-y = 0 \Leftrightarrow x = y [/math]
M2 [math] d(x,y) = \left\Vert x - y \right\Vert = \left\Vert (-1)(y-x) \right\Vert = \left\vert -1 \right\vert \left\Vert y-x \right\Vert = d(y,x) [/math]
M3 [math] d(x,z) = \left\Vert x - z \right\Vert = \left\Vert x - y + y - z \right\Vert \le \left\Vert x - y \right\Vert + \left\Vert y - z \right\Vert = d(x,y)+d(y,z) [/math]
Somit besitzt jeder normierte Vektorraum auch eine Metrik, ist also auch ein metrischer Raum.
Im Gegensatz dazu, ist nicht jeder metrische Vektorraum auch ein normierter Vektorraum, s. Beispiele
Hierarchie Topologischer Räume
Wie gesehen, induziert jede Norm eine Metrik, somit ist jeder normierte Vektorraum auch ein metrischer Raum. Analog dazu induziert jedes Skalarprodukt [math] (\cdot,\cdot) [/math] eine Norm via [math] \left\Vert v \right\Vert = \sqrt{(v.v)} [/math]. Außerdem induziert jede Metrik auf dem metrischen Raum [math] (M,d) [/math] eine Topologie via [math] \ \mathcal{O} := \{U \subset M, U\ \text{ist offen bzgl.}\ d\}. [/math] Somit erhält man die folgende Hierarchie von Räumen:
Metrik Beispiele
Durch Normen induzierte Metriken
Jede Norm die es auf einem Vektorraum gibt induziert wie folgt eine Metrik
- [math]d(x, y) := \|x - y\|[/math]
Daher sehen wir, dass jeder normierte Vektorraum ein metrischer Raum ist.
- Ein weiteres Beispiel ist:
Die euklidische Metrik
In der zweidimensionalen euklidischen Ebene stimmt der euklidische Abstand [math]d(x,y)[/math] mit dem gängigen Gedanken des Abstandes überein.
Sind die Punkte [math]x[/math] und [math]y[/math] durch [math]x=(x_1, \ldots, x_n)[/math] und [math]y=(y_1, \ldots, y_n)[/math] gegeben, so definieren wir die euklidische Metrik wie folgt:
- [math]d(x,y) = \|x-y\|_2 =\sqrt{(x_1 - y_1)^2 + \cdots + (x_n - y_n)^2} = \sqrt{\sum_{i=1}^n (x_i-y_i)^2}[/math]
Der Satz des Phytagoras stellte eine Formel für den Abstandsbegriff in dem kartesischen Koordinatensystem, beispielsweise im n=2 kann man sich die Berechnung des Abstandes wie ein Rechtwinkliges Dreieck vorstellen, durch: [math]c = \sqrt{(x_1-x_0)^2 + (y_1-y_0)^2}[/math] wobei [math]c[/math] den Abstand zwischen den Punkten [math](x_0,y_0), (x_1,y_1)[/math] darstellt. Im Bild rechts könnte man sich die Strecken [math]x_1-x_0[/math] und [math]y_1-y_0[/math] als a und b vorstellen und den berechneten Abstand [math]c[/math] als c. Der euklidische Abstand ist eine Metrik welche die Dreiecksungleichung erfüllt. Die Axiome einer Norm werden ebenfalls erfüllt, somit wird es folglich durch eine Norm induziert, welche man auch die euklidische Norm nennt.
Nicht durch Normen induzierte Metriken
Es gibt Metriken welche die Axiome N1-N3 einer Norm nicht erfüllen ein Beispiel hierfür ist folgende Metrik welche das Axiom N2 nicht erfüllt:
Die Diskrete Metrik
Auf jeder Menge lässt sich die triviale Metrik definieren. Sie wird auch diskrete Metrik gennant und ist dazu noch eine Ultrametrik. Sie wird wie folgt definiert:
- Sei [math]X[/math] eine Menge, [math]x[/math],[math]y[/math] aus [math]X[/math] und [math]d[/math] eine Abbildung [math] d\colon X\times X\to\mathbb R [/math] mit
- [math]d(x,y)=\begin{cases} 0 & \text{für } x = y \\ 1 & \text{für } x\neq y \end{cases}[/math]
Diese Metrik induziert die diskrete Topologie.
Die diskrete Metrik wird nicht durch eine Norm induziert, denn betrachtet man den Punkt N2 einer Norm so sieht man:
Sei [math]\| x \|=d(x,0)[/math] und sei [math]x[/math] ungleich 0 so ist,
[math]\| 2x \|=d(2x,0)=1≠2=2d(x,0)=|2|\| x \|[/math]
Also kann die diskrete Metrik nicht durch eine Norm induziert werden.
Ein weiteres Beispiel, welches nicht alle Axiome einer Norm erfüllt, ist die:
Die SNCF-Metrik
Sei [math]X[/math] eine Menge von Punkten in der Ebene und [math] p [/math] ein fester Punkt.
Dann ist die SNCF-Metrik auf [math]X[/math] wie folgt definiert:
- [math] d\colon X\times X\to\mathbb R [/math]
- [math] d(x,y)=\begin{cases} \|x-y\|&\text{falls } x, y \text{ auf einer Geraden durch } p \text{ liegen, }\\ \|x-p\|+\|p-y\|&\text{sonst}. \end{cases} [/math]
Der Name dieser Metrik leitet sich von der Eisenbahngesellschaft SNCF ab, da diese Metrik in den Kontext des Französischen Eisenbahnnetzes fällt.
Nehme man an X seien die Städte Frankreichs, und [math] p [/math] Paris so kann der Abstand, falls es keinen direkt Zug zwischen der Stadt [math]x[/math] und [math]y[/math] gibt, deutlich länger werden.
Die SNCF-Metrik wird nicht von einer Norm induziert, denn wäre dem so, würde diese Norm die folgende Gleichung erfüllen:
- [math] \| x \| = d(x,0) [/math].
Es ist jedoch, falls [math] p [/math] nicht auf einer Geraden durch [math] 0 [/math] und [math] x [/math] liegt (und damit auch nicht [math] 0 [/math] ist)
- [math] d(x,0) = \| x-p \| + \| p \| \neq \| x \| [/math].
Deshalb gibt es keine Norm, die die SNCF-Metrik induziert.
Spezielle Metriken
Ultrametrik
Eine Metrik nennt man Ultrametrik falls bei der M3 Dreiecksungleichung gilt, dass der Abstand [math]d(x, y)[/math] nicht länger ist als der längere der beiden Abstände [math]d(x, z)[/math] und [math]d(z, y)[/math] und das mit beliebigem [math]z[/math]. Beispielsweise ist die diskrete Metrik eine Ultrametrik.
Pseudometrik
Eine Pseudometrik ist eine Metrik in welcher die Bedingung aus M1 [math]d\left(x,y\right) = 0 \Rightarrow x = y[/math] nicht gilt, somit ist sie positiv semidefinit. Sie wird in der Funtkionalanalysis auch als Halb- oder Semimetrik bezeichnet.
Nicht-archimedische Metriken
Hier wird die M3 Dreiecksungleichung verstärkt oder geschwächt. Ein Beispiel für diese Metrik wäre die Ultrametrik.
Quasimetrik
Verzichtet man auf M2 (Symmetrie) der Axiome so erhält man eine Quasimetrik. Eine Quasimetrik [math]b[/math] erzeugt durch [math]d(x,y):= \tfrac{1}{2} ( b(x,y) + b(y,x) )[/math] eine Metrik auf [math]X[/math].
Prämetrik
Die Prämetrik fordert nur das Axiom M1 (Positive Definitheit).
Norm Beispiele
Normen auf endlichdimensionalen Vektorräumen
Die Betragsnorm
Der Betrag ist das einfachste und am häufigsten auftretende Beispiel einer Norm. Man erhält ihn durch Weglassen des Vorzeichens:
- [math]\| z \| = | z | = \begin{cases} \,\ \ z &\mathrm{f\ddot ur}\ z \ge 0\\ \, -z &\mathrm{f\ddot ur}\ z \lt 0. \end{cases} [/math]
Bei komplexen Zahlen ist der Betrag definiert durch:
- [math]\| z \| = | z | = \sqrt{\left(\operatorname{Re} z\right)^2 + \left(\operatorname{Im} z\right)^2}[/math]
Euklidische Norm
Die euklidische Norm eines Vektors, auch 2-Norm eines Vektors genannt ist definiert als
- [math]\| x \|_2 = \sqrt{\sum_{i=1}^n |x_i|^2}[/math],
wobei mit [math]x_i[/math] die einzelnen Komponenten eines Vektors gemeint sind.
Maximumsnorm
Die Maximumsnorm (auch Unendlich-Norm genannt) eines Vektors ist definiert als
- [math]\| x \|_{\infty} = \max_{i=1, \dotsc, n} |x_i|[/math]
Summennorm
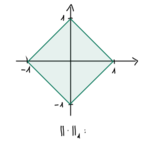
Die Summennorm (auch 1-Norm genannt) eines Vektors ist definiert als
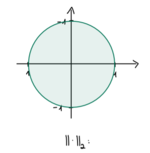
- [math]\| x \|_1 = \sum_{i=1}^n | x_i |[/math]
p-Normen
Man kann für jedes reelles [math]1 \leq p \lt \infty[/math] die [math]p[/math]-Norm eines Vektors, durch
- [math]\| x \|_p = \left(\sum_{i=1}^n | x_i |^p\right)^{1/p}[/math], definieren
Wählt man [math]p=1[/math] erhält man so die Summennorm, für [math]p=2[/math] die euklidische Norm und für [math]p\to\infty[/math] die Maximumsnorm.
| AusklappenBeweis |
Normen auf unendlichdimensionalen Vektorräumen
Supremumsnorm
Die Supremumsnorm einer beschränkten Funktion ist definiert als
- [math]\ \| f \|_{\sup} = \| f \|_{\infty} = \sup_{x \in \Omega} | f(x) |[/math].
Operatornorm
Seien V und W Vektorräume und sei [math]f\colon V \rightarrow W[/math] eine lineare Abbildung. Dann ist die Operatornorm definiert als:
[math]\|f\| = \sup_{x \in V\setminus\{0\}} \frac{\|f(x)\|_W}{\|x\|_V} = \sup_{\|x\|_V = 1} \|f(x)\|_W[/math]
Literatur
Otto Forster - Analysis 2 11.Auflage 2017
Quellen
Autoren
Arian Gjini, Alassane Diagne, Robin Klotzbücher