Matrixgruppen in der Physik: Unterschied zwischen den Versionen
Mateo (Diskussion | Beiträge) |
Mateo (Diskussion | Beiträge) |
||
| (4 dazwischenliegende Versionen desselben Benutzers werden nicht angezeigt) | |||
| Zeile 118: | Zeile 118: | ||
Diese Matrizen beschreiben '''Reskalierungen des Raumes''', also das Stauchen oder Strecken der Koordinatenachsen des Raumes. | Diese Matrizen beschreiben '''Reskalierungen des Raumes''', also das Stauchen oder Strecken der Koordinatenachsen des Raumes. | ||
| − | '''Beispiel''' im | + | '''Beispiel''' im <math>\mathbb{R}^2</math>: |
| + | |||
| + | <math>\begin{pmatrix}2&0\\0&3\end{pmatrix}</math> skaliert den Raum, sodass ein Vektor <math>\begin{pmatrix}1\\1\end{pmatrix}</math> zu dem Vektor <math>\begin{pmatrix}2&0\\0&3\end{pmatrix}\cdot\begin{pmatrix}1\\1\end{pmatrix}=\begin{pmatrix}2\\3\end{pmatrix}</math> wird (siehe Abb. 1). | ||
====2. Zentrische Streckungen==== | ====2. Zentrische Streckungen==== | ||
| − | [[Datei:Zentrisch gestreckter Vektor.jpg|mini|188x188px|Bild eines zentrisch gestreckten Vektors]] | + | [[Datei:Zentrisch gestreckter Vektor.jpg|mini|188x188px|Abb. 2: Bild eines zentrisch gestreckten Vektors]] |
Zur Untergruppe der zentrischen Streckungen gehören all diejenigen Diagonalmatrizen, bei denen alle Diagonalelemente gleich und verschieden von null sind. | Zur Untergruppe der zentrischen Streckungen gehören all diejenigen Diagonalmatrizen, bei denen alle Diagonalelemente gleich und verschieden von null sind. | ||
| − | '''Beispiel''' im | + | '''Beispiel''' im im <math>\mathbb{R}^2</math>: |
| + | |||
| + | <math>\begin{pmatrix}3&0\\0&3\end{pmatrix}</math>ist eine zentrische Streckung um den Faktor 3. Der Vektor <math>\begin{pmatrix}1\\1\end{pmatrix}</math> zu dem Vektor <math>\begin{pmatrix}3&0\\0&3\end{pmatrix}\cdot\begin{pmatrix}1\\1\end{pmatrix}=\begin{pmatrix}3\\3\end{pmatrix}</math> (siehe Abb. 2). | ||
====3. Spezielle lineare Gruppe <math>SL(n, K)</math>==== | ====3. Spezielle lineare Gruppe <math>SL(n, K)</math>==== | ||
| − | Die spezielle lineare Gruppe enthält alle Matrizen | + | Die spezielle lineare Gruppe enthält alle Matrizen der allgemeinen linearen Gruppe, deren Determinante 1 |
beträgt. Daher ist sie ein Normalteiler von <math>GL(n, K)</math>, also ist die durch <math>SL(n, K)</math> gebildete Faktorgruppe <math>GL(n,K)/SL(n, K)</math> isomorph zur Gruppe der Einheiten von <math>K</math> (ohne Null). | beträgt. Daher ist sie ein Normalteiler von <math>GL(n, K)</math>, also ist die durch <math>SL(n, K)</math> gebildete Faktorgruppe <math>GL(n,K)/SL(n, K)</math> isomorph zur Gruppe der Einheiten von <math>K</math> (ohne Null). | ||
In der Physik sind besonders die Untergruppen <math>SO(n)</math> (spezielle orthogonale Gruppe) und <math>SU(n)</math> (spezielle unitäre Gruppe) der speziellen linearen Gruppe von Bedeutung. | In der Physik sind besonders die Untergruppen <math>SO(n)</math> (spezielle orthogonale Gruppe) und <math>SU(n)</math> (spezielle unitäre Gruppe) der speziellen linearen Gruppe von Bedeutung. | ||
| − | ====4. Orthogonale Gruppe <math> | + | ====4. Orthogonale Gruppe <math>O(n, K)</math>==== |
| − | In der orthogonalen Gruppe sind alle orthogonalen Matrizen, | + | In der orthogonalen Gruppe sind alle orthogonalen Matrizen, das sind alle Matrizen, deren Inverses zugleich ihre |
transponierte Matrix ist. In orthogonalen Matrizen sind die Zeilen- und Spaltenvektoren bezüglich des | transponierte Matrix ist. In orthogonalen Matrizen sind die Zeilen- und Spaltenvektoren bezüglich des | ||
Standardskalarprodukts orthonormal zueinander. Die Determinante einer orthogonalen Matrix hat immer den | Standardskalarprodukts orthonormal zueinander. Die Determinante einer orthogonalen Matrix hat immer den | ||
| Zeile 139: | Zeile 143: | ||
=====a. Spezielle orthogonale Gruppe <math>SO(n)</math>===== | =====a. Spezielle orthogonale Gruppe <math>SO(n)</math>===== | ||
| − | [[Datei:Drehung.jpg|mini|237x237px|Bild eines Vektors unter einer Drehung]] | + | [[Datei:Drehung.jpg|mini|237x237px|Abb. 3: Bild eines Vektors unter einer Drehung]] |
| − | Die spezielle orthogonale Gruppe umfasst alle orthogonalen Matrizen mit | + | Die spezielle orthogonale Gruppe umfasst alle orthogonalen Matrizen mit Determinante 1. Physikalisch gesehen beschreiben diese Matrizen '''Drehungen'''. |
| − | In der Physik besonders relevant ist die spezielle orthogonale Gruppe im dreidimensionalen Raum <math>SO(3)</math> | + | In der Physik besonders relevant ist die spezielle orthogonale Gruppe im dreidimensionalen Raum <math>SO(3)</math>. |
| − | + | Matrizen aus <math>SO(3)</math> beschreiben alle Drehungen um eine durch den Koordinatenursprung verlaufende Drehachse | |
im dreidimensionalen Raum. Beispielsweise führen die folgenden Matrizen zu | im dreidimensionalen Raum. Beispielsweise führen die folgenden Matrizen zu | ||
Drehungen um eine der Hauptachsen (x, y oder z) um den winkel <math>\alpha</math>: | Drehungen um eine der Hauptachsen (x, y oder z) um den winkel <math>\alpha</math>: | ||
| Zeile 179: | Zeile 183: | ||
\end{pmatrix}\cdot\begin{pmatrix}1\\1\\3\end{pmatrix}=\begin{pmatrix}0\\\sqrt{2}\\3\end{pmatrix}</math> (siehe Abb. 3) | \end{pmatrix}\cdot\begin{pmatrix}1\\1\\3\end{pmatrix}=\begin{pmatrix}0\\\sqrt{2}\\3\end{pmatrix}</math> (siehe Abb. 3) | ||
| − | Da sie | + | Da sie außerdem das Standard-Skalarprodukt auf <math>\mathbb{R}^3</math> (und damit die Geometrie) invariant lässt, ist diese Gruppe die '''Isometriegruppe des <math>\mathbb{R}^3</math>'''. |
| − | =====b. <math>O(n)\backslash SO(n)</math>===== | + | =====b. Drehspiegelungen <math>O(n)\backslash SO(n)</math>===== |
| − | [[Datei:Drehspiegelung.jpg|mini|230x230px|Bild eines Vektors unter einer Drehspiegelung]] | + | [[Datei:Drehspiegelung.jpg|mini|230x230px|Abb. 4: Bild eines Vektors unter einer Drehspiegelung]] |
Die Menge <math>O(n)\backslash SO(n)</math> umfasst alle orthogonalen Matrizen mit der Determinante -1. Damit umfasst | Die Menge <math>O(n)\backslash SO(n)</math> umfasst alle orthogonalen Matrizen mit der Determinante -1. Damit umfasst | ||
| − | diese Menge | + | diese Menge hpysikalisch gesehen alle '''Drehspiegelungen'''. Da zwei hintereinander ausgeführte Drehspiegelungen jedoch einer einfachen Drehung (und nicht wieder einer Drehspiegelung) entsprechen, ist diese Menge nicht abgeschlossen und damit keine Gruppe. Elemente aus <math>O(n)\backslash SO(n)</math>lassen sich, ähnlich wie Drehungen, beispielsweise durch folgende Matrizen darstellen: |
<math> | <math> | ||
| Zeile 211: | Zeile 215: | ||
</math> | </math> | ||
| − | Wird nun eine solche Drehspiegelungsmatrix für die Drehachse z und <math>\alpha=45^\circ</math> auf den Vektor <math>\begin{pmatrix}1\\1\\3\end{pmatrix}</math> angewendet, so ergibt sich der neue Vektor <math>\begin{pmatrix} | + | Wird nun beispielsweise eine solche Drehspiegelungsmatrix für die Drehachse z und <math>\alpha=45^\circ</math> auf den Vektor <math>\begin{pmatrix}1\\1\\3\end{pmatrix}</math> angewendet, so ergibt sich der neue Vektor <math>\begin{pmatrix} |
\cos 45^\circ&-\sin45^\circ&0\\ | \cos 45^\circ&-\sin45^\circ&0\\ | ||
\sin45^\circ&\cos45^\circ&0\\ | \sin45^\circ&\cos45^\circ&0\\ | ||
| Zeile 218: | Zeile 222: | ||
====Unitäre Gruppe <math>U(n)</math>==== | ====Unitäre Gruppe <math>U(n)</math>==== | ||
| − | Die unitäre Gruppe über dem Körper der komplexen Zahlen umfasst alle | + | Die unitäre Gruppe über dem Körper der komplexen Zahlen ist eine Gruppe nicht reeller Matrizen. Sie umfasst alle unitären Matrizen, das sind all diejenigen |
Matrizen, deren hermitesch transponierte (also transponierte und komplex konjugierte) Matrix zugleich das | Matrizen, deren hermitesch transponierte (also transponierte und komplex konjugierte) Matrix zugleich das | ||
Inverse der Matrix ist. In der Physik ist diese Matrixgruppe von entscheidender Bedeutung bei der Beschreibung | Inverse der Matrix ist. In der Physik ist diese Matrixgruppe von entscheidender Bedeutung bei der Beschreibung | ||
von '''Symmetrien der Wellenfunktion''' in der Quantenphysik. | von '''Symmetrien der Wellenfunktion''' in der Quantenphysik. | ||
Wie die orthogonale Gruppe hat auch die unitäre Gruppe eine Untergruppe all jener Matrizen, deren | Wie die orthogonale Gruppe hat auch die unitäre Gruppe eine Untergruppe all jener Matrizen, deren | ||
| − | Determinante 1 ist. Diese Untergruppe heißt und ist eine kompakte Lie-Gruppe und differenzierbare Mannigfaltigkeit. | + | Determinante 1 ist. Diese Untergruppe heißt spezielle unitäre Gruppe <math>SU(n)</math> und ist eine kompakte Lie-Gruppe und differenzierbare Mannigfaltigkeit. |
== Beispiel: Matrizenoptik == | == Beispiel: Matrizenoptik == | ||
| Zeile 293: | Zeile 297: | ||
\vdots &\ddots & \vdots \\ | \vdots &\ddots & \vdots \\ | ||
\delta_{n1} & \cdots & \delta_{nn} | \delta_{n1} & \cdots & \delta_{nn} | ||
| + | \end{bmatrix} | ||
| + | = | ||
| + | \begin{bmatrix} | ||
| + | 1 & \quad & 0 \\ | ||
| + | \quad &\ddots & \quad \\ | ||
| + | 0 & \quad & 1 | ||
\end{bmatrix} | \end{bmatrix} | ||
</math> | </math> | ||
| Zeile 298: | Zeile 308: | ||
gemeint ist. | gemeint ist. | ||
| − | Der Trägheitstensor, einer "Verallgemeinerung" des Trägheitsmomentes, gibt an, wie träge ein Körper gegenüber einer Änderung der Winkelgeschwindigkeit um eine seiner Achsen ist. Im Trägheitstensor ist diese Eigenschaft bezüglich verschiedener Achsen dargestellt, und er wird zumeist als Matrix notiert. Dabei entsprechen z. B. symmetrische Darstellungen oder Matrizen in Diagonalgestalt direkt den physikalischen Eigenschaften des Objektes, u. a. in Form von Symmetrien. | + | Der Trägheitstensor, einer "Verallgemeinerung" des Trägheitsmomentes, gibt an, wie träge ein Körper gegenüber einer Änderung der Winkelgeschwindigkeit um eine seiner Achsen ist. Im Trägheitstensor ist diese Eigenschaft bezüglich verschiedener Achsen dargestellt, und er wird zumeist als Matrix notiert. Dabei entsprechen z. B. symmetrische Darstellungen oder Matrizen in Diagonalgestalt direkt den physikalischen Eigenschaften des Objektes, u. a. in Form von Symmetrien. Die jeweiligen Einträge bezeichnen dabei die Trägheitsmomente in die entsprechenden Richtungen (im Koordinatensystem mit 1-,2- und 3-Achse). |
<math>I= \begin{bmatrix} | <math>I= \begin{bmatrix} | ||
| Zeile 314: | Zeile 324: | ||
\end{bmatrix} </math> | \end{bmatrix} </math> | ||
| − | Im Lagrange-Formalismus der klassischen Mechanik lässt sich die Lagrange-Funktion | + | Im Lagrange-Formalismus der klassischen Mechanik lässt sich die Lagrange-Funktion. Zentraler Bestandteil des analystischen Lösungsprozesses zur Bestimmung der Bewegungsgleichungen eines Systems ist es, ein Extremum jener Lagrange-Funktion zu finden; mitunter lässt sie sich auch durch Matrizen darstellen. Dadurch ist die Berechnung vereinfacht und es können bestimmte Eigenschaften des Systems, z. B. Schwingungsfrequenzen (sog. Normalmoden), bestimmt werden. Hierbei wird zwar der Matrizenformalismus zur Berechnung genutzt, zugleich muss aber beachtet werden, inwiefern diese Matrix physikalische Realität besitzt, d. h. ob sie nur eine Art von "Wertesammlung" darstellt oder eine tatsächliche Transformation. Dieses Argument wird bspw. verwendet, um die Symmetrie jener Matrix zu begründen, denn wenn die Matrix nur dazu dient, bestimmte Elemente durch die entsprechenden Indizes zuzuordnen und durch Multiplikation mit passenden Vektoren eine bestimmte Gleichung zu liefern, so dürfte es keinen Unterschied machen, welche Reihenfolge die Indizes haben. |
In der Elektrotechnik werden häufig lineare Gleichungssysteme von Schaltkreisen mithilfe von Matrizenmultiplikation beschrieben. | In der Elektrotechnik werden häufig lineare Gleichungssysteme von Schaltkreisen mithilfe von Matrizenmultiplikation beschrieben. | ||
| Zeile 320: | Zeile 330: | ||
Auch die Jacobi- und Hessematrix werden in der Physik genutzt, z. B. bei der Transformation von Integralen oder bei der mehrdimensionalen Taylorentwicklung. | Auch die Jacobi- und Hessematrix werden in der Physik genutzt, z. B. bei der Transformation von Integralen oder bei der mehrdimensionalen Taylorentwicklung. | ||
| − | <references /> | + | == Referenz == |
| + | <references /><small>dieser Wiki-Eintrag wurde von Antonia Kersten, Konrad Kockler und Mateo Cárdenes Wuttig erstellt</small> | ||
Aktuelle Version vom 12. Oktober 2021, 10:34 Uhr
Matrizen haben in der Physik eine zentrale Bedeutung, da sie lineare Abbildungen zwischen Vektorräumen repräsentieren. Im Folgenden werden einige Beispiele von Matrixgruppen und Matrizen in der Physik aufgezeigt. Dabei wird deutlich, dass einerseits sowohl der Gruppencharakter von Matrizen, andererseits aber auch die Nutzung von Matrizen an sich von großer Bedeutung ist.
Grundbegriffe der Gruppentheorie
Allgemeine Definition
In der Mathematik bezeichnet der Begriff der Gruppe [math](G,\cdot)[/math] ein Tupel bestehend aus einer Menge [math]G[/math] und einer wohldefinierten Abbildung [math]\cdot : G\times G\to G;\ (x,y)\mapsto x\cdot y[/math] welche folgende Eigenschaften, genannt Gruppenaxiome, erfüllt:
|
[math]\forall a,b,c\in G:[/math] | [math](a\cdot b)\cdot c=a\cdot(b\cdot c)[/math] | ||
|
[math]\exists! e\in G\ \forall a\in G:[/math] | [math]e\cdot a=a\cdot e=a[/math] | ||
|
[math]\forall a\in G\ \exists !a^{-1}\in G:\quad[/math] | [math]a\cdot a^{-1}=a^{-1}\cdot a=e[/math] |
Wichtig hier ist, dass das neutrale Element [math]e[/math], sowie für jedes Gruppenelement [math]a[/math] das Inverse [math]a^{-1}[/math] eindeutig ist.
Eine Gruppe heißt abelsch, falls sie zudem noch ein viertes Axiom erfüllt:
|
[math]\forall a,b\in G:[/math] | [math] a\cdot b=b\cdot a [/math] |
Beispiele:
- [math](\mathbb{Z},+)[/math]: Die ganzen Zahlen mit der gewöhnlichen Addition bilden eine abelsche Gruppe. Das neutrale Element ist die 0 und das Inverse zu einer ganzen Zahl [math]n[/math] ist [math]-n[/math].
- [math](\mathbb{Q}\backslash\{0\},\cdot)[/math]: Die rationalen Zahlen ohne die Null bilden mit der Multiplikation eine abelsche Gruppe.
- [math](S_n,\circ)[/math]: Die symmetrische Gruppe vom Grad [math]n[/math] ist mit der Komposition (bzw. Hintereinanderausführung) eine Gruppe. Für [math]n\geq3[/math] ist sie jedoch nicht abelsch.
Untergruppen
Als Untergruppe [math](U,\cdot)\subset (G,\cdot)[/math] bezeichnet man eine nichtleere Teilmenge einer Gruppe [math](G,\cdot)[/math] welche selber wieder eine Gruppe ist, d.h. wieder die Gruppenaxiome erfüllt. Insbesondere ist sie abgeschlossen, d.h. es gilt [math]\forall a,b\in U:\ \ a\cdot b\in U[/math]
Eine äquivalente Definition ist, dass eine nichtleere Teilmenge [math]U\subset G[/math] genau dann eine Untergruppe ist, falls gilt:
- [math]\forall a,b\in U: \quad a\cdot b^{-1}\in U[/math]
| Beweis der Äquivalenz |
| Wir beweisen die Äquivalenz, indem wir die Hin- und Rückrichtung beweisen:
[math] \Rightarrow [/math]: Folgt direkt aus der Abgeschlossenheit der Gruppen und der Gruppenaxiome. [math]\Leftarrow[/math]: Hierzu müssen wir die Gruppenaxiome überprüfen: Assoziativität: Da für alle Elemente der Untergruppe die Verknüpfung nach wie vor noch innerhalb der Gruppe geschieht, wird die Assoziativität von der Obergruppe [math]G[/math] vererbt. Neutrales Element: Sei ein [math]a\in U[/math] gegeben. Da [math]U[/math] nichtleer ist, existiert (unter Verwendung des Auswahlaxioms) ein solches Element. Somit folgt nach Vorraussetzung:
Somit ist das neutrale Element [math]e[/math] in [math]U[/math] erhalten. Inverses Element: Sei ein [math]a\in U[/math] gegeben. Wie oben gezeigt, ist das neutrale Element in U enthalten. Somit gilt nach Vorraussetzung:
Somit ist für jedes Element in [math]U[/math] auch das Inverse in [math]U[/math] enthalten. Die Eindeutigkeit folgt aus der Eindeutigkeit des Inversen in [math]G[/math]. Damit erfüllt [math]U[/math] alle Gruppenaxiome und die beiden Definitionen sind äquivalent. |
Aus dieser Definition folgen direkt einige Eigenschaften von Untergruppen:
- Das neutrale Element ist in jeder Untergruppe enthalten.
- Für jedes Element einer Untergruppe ist auch das Inverse in der Untergruppe enthalten.
- Der Schnitt zweier Untergruppen ist wieder eine Untergruppe.
Lie-Gruppen
Eine für die Physik besonders wichtige Klasse von Gruppen sind sogenannte (reelle) Lie-Gruppen (benannt nach dem norwegischen Mathematiker Sophus Lie). Diese sind reellle, differenzierbare Mannigfaltigkeiten (also Mengen (im reellen fall Teilmengen des [math]\mathbb{R}^m[/math]), welche lokal wie der [math]\mathbb{R}^n[/math] ([math] m\geq n[/math]) aussehen), welche mit einer Gruppenstruktur versehen sind. Dabei muss die Verknüpfung und die Inversenbildung beliebig oft differenzierbar sein :
- [math]\left(\cdot: G\times G\to G\right)\in C^\infty[/math]
- [math]\left(i:G\to G; x\mapsto i(x)=x^{-1}\right)\in C^\infty[/math]
Wichtig ist, dass eine Untergruppe einer Lie-Gruppe nicht zwangsweise wieder eine Lie-Gruppe sein muss.
Beispiel: die allgemeine lineare Gruppe [math]GL_n(\mathbb{R})[/math]
Die allgemeine lineare Gruppe [math]GL_n(\mathbb{R})[/math], die Menge aller invertierbaren [math]n\times n[/math]-Matrizen mit reellen Einträgen, ist eine Lie-Gruppe ([math]GL_n(\mathbb{R})[/math] ist eine offene Teilmenge der [math]n\times n[/math]- Matrizen [math]Mat(n\times n,\mathbb{R})[/math], welche wir mit dem [math]\mathbb{r}^{n^2}[/math] identifizieren können, und damit eine glatte, reellwertige Mannigfaltigkeit). Die Matrixmultiplikation [math]m[/math] und die Inversenbildung [math]i[/math] sind differenzierbar mit folgenden Differentialen:
- [math] \begin{array}{ll} D_{\hat{A},\hat{B}}m(A,b)=\hat{A}B+A\hat{B} &\forall\hat{A},\hat{B},A,B\in GL_n(\mathbb{R})\\ D_{\hat{A}}i(A)=-A^{-1}\hat{A}A^{-1} &\forall\hat{A},A\in GL_n(\mathbb{R}) \end{array}[/math]
Induktiv folgt damit, dass beide Abbildungen glatt sind, da die Differentiale wieder differenzierbar sind.
Matrizen und Matrixgruppen
Eine Matrix ist eine Anordnung von mathematischen Objekten in Rechteckform, für die bestimmte Rechenoperationen definiert sind. In der Physik werden sie sowohl als Darstellung linearer Abbildungen als auch als Wertesammlung und zur Lösung linearer Gleichungssysteme genutzt. Dabei wird häufig auf Konzepte der Eineindeutigkeit, d. h. Umkehrbarkeit, oder Symmetrie zurückgegriffen, wenn mit Matrizen gearbeitet wird.
Häufig werden in der Physik Matrizen zur Beschreibung von Transformationen eines Objektes im Raum genutzt. Insbesondere werden anschauliche lineare Abbildungen im zwei- und dreidimensionalen Raum häufig genutzt, vierdimensionale Matrizen sind z. B. bei relativistischen Berechnungen häufig anzutreffen. Höherdimensionale Matrizen sind spielen häufig eine untergeordnete Rolle. Dabei ist mitunter weniger der Gruppencharakter als die elegante Beschreibung und einfache Berechnung von Bedeutung. Nichtsdestotrotz sollen auch solche Matrizen erwähnt werden.
Allgemeine lineare Gruppe [math]GL_n(K)[/math]
Die allgemeine lineare Gruppe [math]GL(n,K)[/math] oder [math]GL_n(K)[/math] auch (vom englischen "general linear group") heißt vom Grad n und über dem Körper K. Weitere Schreibweisen sind [math]GL(n,q)[/math], wenn der Körper K endlich ist und die Primzahlpotenz q hat, und [math]GL(n)[/math] beziehungsweise [math]GL_n[/math] , wenn es sich bei dem Körper um die reellen oder komplexen Zahlen handelt.
Sie umfasst alle invertierbaren [math]n\times n[/math]-Matrizen mit Koeffizienten aus dem Körper K. Die Verknüpfung der Elemente der Gruppe erfolgt durch die Matrixmultiplikation. Die allgemeine lineare Gruppe und einige ihrer Untergruppen werden in der Physik zur Untersuchung von Symmetrien genutzt.
In der Physik bedeutsame Untergruppen der allgemeinen linearen Gruppe
1. Untergruppe der Diagonalmatrizen
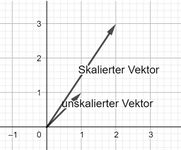
Die Untergruppe der Diagonalmatrizen enthält all diejenigen quadratischen Matrizen der allgemeinen linearen Gruppe, die nur auf der Hauptdiagonalen von null verschiedene Elemente aufweisen. Bei Matrizen dieser Untergruppe müssen alle Elemente der Hauptdiagonalen ungleich null sein. Diese Matrizen beschreiben Reskalierungen des Raumes, also das Stauchen oder Strecken der Koordinatenachsen des Raumes.
Beispiel im [math]\mathbb{R}^2[/math]:
[math]\begin{pmatrix}2&0\\0&3\end{pmatrix}[/math] skaliert den Raum, sodass ein Vektor [math]\begin{pmatrix}1\\1\end{pmatrix}[/math] zu dem Vektor [math]\begin{pmatrix}2&0\\0&3\end{pmatrix}\cdot\begin{pmatrix}1\\1\end{pmatrix}=\begin{pmatrix}2\\3\end{pmatrix}[/math] wird (siehe Abb. 1).
2. Zentrische Streckungen
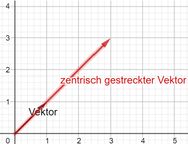
Zur Untergruppe der zentrischen Streckungen gehören all diejenigen Diagonalmatrizen, bei denen alle Diagonalelemente gleich und verschieden von null sind.
Beispiel im im [math]\mathbb{R}^2[/math]:
[math]\begin{pmatrix}3&0\\0&3\end{pmatrix}[/math]ist eine zentrische Streckung um den Faktor 3. Der Vektor [math]\begin{pmatrix}1\\1\end{pmatrix}[/math] zu dem Vektor [math]\begin{pmatrix}3&0\\0&3\end{pmatrix}\cdot\begin{pmatrix}1\\1\end{pmatrix}=\begin{pmatrix}3\\3\end{pmatrix}[/math] (siehe Abb. 2).
3. Spezielle lineare Gruppe [math]SL(n, K)[/math]
Die spezielle lineare Gruppe enthält alle Matrizen der allgemeinen linearen Gruppe, deren Determinante 1 beträgt. Daher ist sie ein Normalteiler von [math]GL(n, K)[/math], also ist die durch [math]SL(n, K)[/math] gebildete Faktorgruppe [math]GL(n,K)/SL(n, K)[/math] isomorph zur Gruppe der Einheiten von [math]K[/math] (ohne Null). In der Physik sind besonders die Untergruppen [math]SO(n)[/math] (spezielle orthogonale Gruppe) und [math]SU(n)[/math] (spezielle unitäre Gruppe) der speziellen linearen Gruppe von Bedeutung.
4. Orthogonale Gruppe [math]O(n, K)[/math]
In der orthogonalen Gruppe sind alle orthogonalen Matrizen, das sind alle Matrizen, deren Inverses zugleich ihre transponierte Matrix ist. In orthogonalen Matrizen sind die Zeilen- und Spaltenvektoren bezüglich des Standardskalarprodukts orthonormal zueinander. Die Determinante einer orthogonalen Matrix hat immer den Betrag 1. Damit lässt sich die orthogonale Gruppe in zwei disjunkte Untergruppen aufteilen: die orthogonalen Matrizen mit Determinante 1 und die orthogonalen Matrizen mit Determinante -1.
a. Spezielle orthogonale Gruppe [math]SO(n)[/math]
Die spezielle orthogonale Gruppe umfasst alle orthogonalen Matrizen mit Determinante 1. Physikalisch gesehen beschreiben diese Matrizen Drehungen.
In der Physik besonders relevant ist die spezielle orthogonale Gruppe im dreidimensionalen Raum [math]SO(3)[/math].
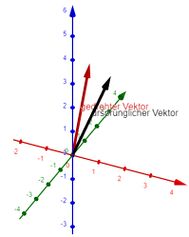
Matrizen aus [math]SO(3)[/math] beschreiben alle Drehungen um eine durch den Koordinatenursprung verlaufende Drehachse im dreidimensionalen Raum. Beispielsweise führen die folgenden Matrizen zu Drehungen um eine der Hauptachsen (x, y oder z) um den winkel [math]\alpha[/math]:
[math] \begin{align*} R_x(\alpha)&= \begin{pmatrix} 1&0&0\\ 0&\cos\alpha&-\sin\alpha\\ 0&\sin\alpha&\cos\alpha \end{pmatrix}\\ R_y(\alpha)&= \begin{pmatrix} \cos\alpha&0&\sin\alpha\\ 0&1&0\\ -\sin\alpha&0&\cos\alpha \end{pmatrix}\\ R_y(\alpha)&= \begin{pmatrix} \cos\alpha&-\sin\alpha&0\\ \sin\alpha&\cos\alpha&0\\ 0&0&1 \end{pmatrix} \end{align*} [/math]
Wird also beispielsweise der Vektor [math]\begin{pmatrix}1\\1\\3\end{pmatrix}[/math] um einen Winkel von 45° um die z-Achse rotiert, so ergibt sich der Vektor [math]\begin{pmatrix} \cos 45^\circ&-\sin45^\circ&0\\ \sin45^\circ&\cos45^\circ&0\\ 0&0&1 \end{pmatrix}\cdot\begin{pmatrix}1\\1\\3\end{pmatrix}=\begin{pmatrix}0\\\sqrt{2}\\3\end{pmatrix}[/math] (siehe Abb. 3)
Da sie außerdem das Standard-Skalarprodukt auf [math]\mathbb{R}^3[/math] (und damit die Geometrie) invariant lässt, ist diese Gruppe die Isometriegruppe des [math]\mathbb{R}^3[/math].
b. Drehspiegelungen [math]O(n)\backslash SO(n)[/math]
Die Menge [math]O(n)\backslash SO(n)[/math] umfasst alle orthogonalen Matrizen mit der Determinante -1. Damit umfasst diese Menge hpysikalisch gesehen alle Drehspiegelungen. Da zwei hintereinander ausgeführte Drehspiegelungen jedoch einer einfachen Drehung (und nicht wieder einer Drehspiegelung) entsprechen, ist diese Menge nicht abgeschlossen und damit keine Gruppe. Elemente aus [math]O(n)\backslash SO(n)[/math]lassen sich, ähnlich wie Drehungen, beispielsweise durch folgende Matrizen darstellen:
[math] \begin{align*} R_x(\alpha)&= \begin{pmatrix} -1&0&0\\ 0&\cos\alpha&-\sin\alpha\\ 0&\sin\alpha&\cos\alpha \end{pmatrix}\\ R_y(\alpha)&= \begin{pmatrix} \cos\alpha&0&\sin\alpha\\ 0&-1&0\\ -\sin\alpha&0&\cos\alpha \end{pmatrix}\\ R_y(\alpha)&= \begin{pmatrix} \cos\alpha&-\sin\alpha&0\\ \sin\alpha&\cos\alpha&0\\ 0&0&-1 \end{pmatrix} \end{align*} [/math]
Wird nun beispielsweise eine solche Drehspiegelungsmatrix für die Drehachse z und [math]\alpha=45^\circ[/math] auf den Vektor [math]\begin{pmatrix}1\\1\\3\end{pmatrix}[/math] angewendet, so ergibt sich der neue Vektor [math]\begin{pmatrix} \cos 45^\circ&-\sin45^\circ&0\\ \sin45^\circ&\cos45^\circ&0\\ 0&0&-1 \end{pmatrix}\cdot\begin{pmatrix}1\\1\\3\end{pmatrix}=\begin{pmatrix}0\\\sqrt{2}\\-3\end{pmatrix}[/math] (siehe Abb. 4)
Unitäre Gruppe [math]U(n)[/math]
Die unitäre Gruppe über dem Körper der komplexen Zahlen ist eine Gruppe nicht reeller Matrizen. Sie umfasst alle unitären Matrizen, das sind all diejenigen Matrizen, deren hermitesch transponierte (also transponierte und komplex konjugierte) Matrix zugleich das Inverse der Matrix ist. In der Physik ist diese Matrixgruppe von entscheidender Bedeutung bei der Beschreibung von Symmetrien der Wellenfunktion in der Quantenphysik. Wie die orthogonale Gruppe hat auch die unitäre Gruppe eine Untergruppe all jener Matrizen, deren Determinante 1 ist. Diese Untergruppe heißt spezielle unitäre Gruppe [math]SU(n)[/math] und ist eine kompakte Lie-Gruppe und differenzierbare Mannigfaltigkeit.
Beispiel: Matrizenoptik
Ein Beispiel für Matrizen in der Experimentalphysik ist die sogenannte Matrizenoptik. Unter der Prämisse der geradlinigen Ausbreitung von Lichtstrahlen, die als Geraden behandelt werden können, lassen sich optische Systeme mithilfe von linearen Transformationen leicht berechnen. Betrachtet man die Ausbreitung eines Lichtstrahls unter einem kleinen Winkel zu einer Achse, so ist jener Strahl durch den Winkel und die Entfernung auf der Achse vollständig bestimmt. Die Linearisierung tan(α) = α erlaubt es, den Strahl als Vektor mit den Komponenten des Abstandes und des Winkels zu beschreiben. Es gilt also für den Vektor [math]\textbf{r} = (r, \alpha)[/math], der einen Lichtstrahl charakterisiert, dass das Zurücklegen einer Strecke [math]b[/math]entlang der jeweiligen Achse durch eine Matrix beschrieben werden kann, die im einfachen Fall zweier Dimensionen durch
[math]\begin{bmatrix} 1 & b \\ 0 & 1 \end{bmatrix}[/math]
gegeben ist. Der Lichtstrahl wird also, nachdem er die Strecke [math]b[/math]entlang der Achse unter einem Winkel α zurückgelegt hat, durch
[math]\textbf{r} = \begin{bmatrix} 1 & b \\ 0 & 1 \end{bmatrix} (r, \alpha) = (r + \alpha b , \alpha) [/math]
beschrieben. Konvention ist häufig, die Achse, bezüglich derer die Propagation, d. h. Ausbreitung des Lichtstrahls berechnet wird, als z-Achse zu benennen. Zudem gilt zumeist: die Strahlrichtung läuft von links nach rechts, die Steigung ist positiv, wenn der Strahl von der Achse wegläuft, und es werden bestimmte Annahmen bezüglich des Vorzeichens des Radiuses von Flächen, der Bildweite und -größe getroffen. Folgende Matrizen können angewandt werden, um typische Operationen zu berechnen:
| Operation | Matrix |
|---|---|
| Translation | [math]\begin{bmatrix} 1 & b \\ 0 & 1 \end{bmatrix} [/math] |
| Brechung | [math]\begin{bmatrix} 1 & 0 \\ 0 & \frac{n_1}{n_2} \end{bmatrix} [/math] |
| dünne Linse | [math]\begin{bmatrix} 1 & 0 \\ -\frac{1}{f} & 1 \end{bmatrix} [/math] |
| gekrümmter Spiegel | [math]\begin{bmatrix} 1 & 0 \\ -\frac{2}{r} & 1 \end{bmatrix} [/math] |
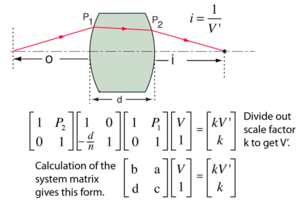
Jene Operationen meinen dabei den Effekt bestimmter optischer Bauteile auf ein Strahlengang. Hierbei stehen [math]n_1, n_2[/math] für die Brechungsindices der Medien, die das Licht in dieser Reihenfolge passiert, [math]f[/math] für die Brennweite der Linse und [math]r[/math] für den Radius des gekrümmten Spiegels. Auch komplexere Elemente wie andere Linsen und Spiegel oder Fasern lassen sich so beschreiben. Dieser Formalismus erlaubt durch Hintereinanderausführung eine vergleichsweise einfache Berechnung selbst von Aufbauten, die viele optische Elemente enthalten. Dies lässt sich in der Abbildung rechts erkennen, wo die Wirkung einer dicken Linse, die an beiden Seiten konvex nach außen gewölbt ist, auf den Strahlengang durch die Hintereinanderausführung von Matrizen beschrieben werden kann. Klassische Eigenschaften von Matrizen wie z. B. die Determinante sind auch hier bedeutsam, beispielsweise muss die Determinante einer Translationsmatrix immer eins sein, allerdings nur vom Betrag, da auch Spiegelungen zugelassen sind.[1]
Andere Anwendungen von Matrizen
Mitunter werden Matrizen auch nicht im Sinne einer Transformation, sondern als eine Darstellung z. B. für einen Tensor oder einen Gewichtungsfaktor genutzt.
So ist bspw. das Kronecker-Delta, insofern als Tensor betrachtet, eine 2x2-Einheitsmatrix. Häufig wird in der Physik folgende Darstellung verwendet
[math]\delta_{ij} = \begin{bmatrix} \delta_{11} & \delta_{12} \\ \delta_{21} & \delta_{22} \end{bmatrix} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} [/math]
wobei damit eigentlich
[math](\delta_{ij})_{i,j \in \{ 1, ..., n\}}= \begin{bmatrix} \delta_{11} & \cdots & \delta_{1n} \\ \vdots &\ddots & \vdots \\ \delta_{n1} & \cdots & \delta_{nn} \end{bmatrix} = \begin{bmatrix} 1 & \quad & 0 \\ \quad &\ddots & \quad \\ 0 & \quad & 1 \end{bmatrix} [/math]
gemeint ist.
Der Trägheitstensor, einer "Verallgemeinerung" des Trägheitsmomentes, gibt an, wie träge ein Körper gegenüber einer Änderung der Winkelgeschwindigkeit um eine seiner Achsen ist. Im Trägheitstensor ist diese Eigenschaft bezüglich verschiedener Achsen dargestellt, und er wird zumeist als Matrix notiert. Dabei entsprechen z. B. symmetrische Darstellungen oder Matrizen in Diagonalgestalt direkt den physikalischen Eigenschaften des Objektes, u. a. in Form von Symmetrien. Die jeweiligen Einträge bezeichnen dabei die Trägheitsmomente in die entsprechenden Richtungen (im Koordinatensystem mit 1-,2- und 3-Achse).
[math]I= \begin{bmatrix} I_{11} & I_{12} & I_{13} \\ I_{21} & I_{22} & I_{23} \\ I_{31} & I_{32} & I_{33} \end{bmatrix} [/math],
Trägheitstensor einer Punktmasse m mit Abstand r auf der x-Achse:
[math]I= m r^2 \begin{bmatrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} [/math]
Im Lagrange-Formalismus der klassischen Mechanik lässt sich die Lagrange-Funktion. Zentraler Bestandteil des analystischen Lösungsprozesses zur Bestimmung der Bewegungsgleichungen eines Systems ist es, ein Extremum jener Lagrange-Funktion zu finden; mitunter lässt sie sich auch durch Matrizen darstellen. Dadurch ist die Berechnung vereinfacht und es können bestimmte Eigenschaften des Systems, z. B. Schwingungsfrequenzen (sog. Normalmoden), bestimmt werden. Hierbei wird zwar der Matrizenformalismus zur Berechnung genutzt, zugleich muss aber beachtet werden, inwiefern diese Matrix physikalische Realität besitzt, d. h. ob sie nur eine Art von "Wertesammlung" darstellt oder eine tatsächliche Transformation. Dieses Argument wird bspw. verwendet, um die Symmetrie jener Matrix zu begründen, denn wenn die Matrix nur dazu dient, bestimmte Elemente durch die entsprechenden Indizes zuzuordnen und durch Multiplikation mit passenden Vektoren eine bestimmte Gleichung zu liefern, so dürfte es keinen Unterschied machen, welche Reihenfolge die Indizes haben.
In der Elektrotechnik werden häufig lineare Gleichungssysteme von Schaltkreisen mithilfe von Matrizenmultiplikation beschrieben.
Auch die Jacobi- und Hessematrix werden in der Physik genutzt, z. B. bei der Transformation von Integralen oder bei der mehrdimensionalen Taylorentwicklung.
Referenz
- ↑ "Optik, Licht und Laser", 3. Auflage, Meschede, Dieter, Vieweg+Teubner, S. 20 - 33
dieser Wiki-Eintrag wurde von Antonia Kersten, Konrad Kockler und Mateo Cárdenes Wuttig erstellt