Euklidischer Algorithmus und Kettenbrüche: Unterschied zwischen den Versionen
Ip253 (Diskussion | Beiträge) |
|||
| (255 dazwischenliegende Versionen von 5 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
Diese Seite behandelt den simplen, aber zugleich genialen Euklidischen Algorithmus und wie dieser mit der Kettenbruchdarstellung rationaler und irrationaler Zahlen zusammenhängt. | Diese Seite behandelt den simplen, aber zugleich genialen Euklidischen Algorithmus und wie dieser mit der Kettenbruchdarstellung rationaler und irrationaler Zahlen zusammenhängt. | ||
= Der Euklidische Algorithmus = | = Der Euklidische Algorithmus = | ||
| − | Schon 300 vor Christus befasste sich Euklid in seinem berühmten Werk "Die Elemente" mit der Frage, wie man das größte gemeinsame Maß, also den größten gemeinsamen Teiler (ggT) zweier Zahlen finden kann. | + | Schon 300 vor Christus befasste sich Euklid in seinem berühmten Werk "Die Elemente" mit der Frage, wie man das größte gemeinsame Maß, also den größten gemeinsamen Teiler (<math> ggT </math>) zweier Zahlen finden kann. |
Er entwickelte dazu einen Algorithmus, der auf folgendem Lemma beruht: | Er entwickelte dazu einen Algorithmus, der auf folgendem Lemma beruht: | ||
| − | '''Lemma:''' Es seien a, b | + | '''Lemma:''' Es seien <math> a, b, q, r \in \mathbb{N} </math> und <math> b > 0 </math> mit |
| − | a = bq + r, | + | :<math> a = bq + r, \hspace{20pt} 0 \le r < b </math> |
| − | Dann gilt ggT(a, b) = ggT(b, r). | + | Dann gilt:<math> \hspace{10pt} ggT(a, b) = ggT(b, r). </math> |
{| class="wikitable mw-collapsible" | {| class="wikitable mw-collapsible" | ||
|+Beweis | |+Beweis | ||
| − | |a = bq + r, also ist jeder gemeinsame Teiler von b und r auch ein Teiler von | + | |Es gilt <math> a = bq + r </math>, also ist jeder gemeinsame Teiler von <math> b </math> und <math> r </math> auch ein Teiler von |
| − | |||
| − | Die Zahlenpaare (a, b) und (b, r) haben also die gleichen gemeinsamen Teiler und somit auch den gleichen ggT. | + | <math> a </math>. |
| + | Stellt man die Gleichung nach <math> r </math> um, erhält man <math> r = a - bq </math> und somit ist | ||
| + | jeder gemeinsame Teiler von <math> a </math> und <math> b </math> auch ein Teiler von <math> r </math>. | ||
| + | |||
| + | Die Zahlenpaare <math> (a, b) </math> und <math> (b, r) </math> haben | ||
| + | also die gleichen gemeinsamen Teiler und somit auch den gleichen <math> ggT </math>. | ||
|} | |} | ||
== Funktionsweise == | == Funktionsweise == | ||
| − | Gesucht ist nun | + | Gesucht ist nun der größte gemeinsame Teiler zweier ganzer Zahlen <math> a </math> und <math> b </math> mit <math> a > b </math>. Der Algorithmus funktioniert wie folgt: |
| − | # Teile a durch b und erhalten den Rest r. | + | # Teile <math> a </math> durch <math> b </math> und erhalten den Rest <math> r </math>. |
| − | # Ist r = 0, ist a ohne Rest durch b teilbar und es gilt ggT(a, b) = b. Ist r | + | # Ist <math> r = 0 </math>, ist <math> a </math> ohne Rest durch <math> b </math> teilbar und es gilt <math> ggT(a, b) = b </math>. |
| − | # Führe die Schritte solange durch, bis Rest 0 bleibt. Der letzte Rest, der von 0 verschieden ist, ist der größte gemeinsame Teiler von a und b. | + | # Ist <math> r \neq 0 </math>, führe Schritt 1 für <math> b </math> und <math> r </math> durch. |
| + | # Führe die Schritte solange durch, bis Rest <math> 0 </math> bleibt. Dann lässt sich die Zahl als Produkt zweier anderer natürlicher Zahlen schreiben und es gilt: | ||
| + | Der letzte Rest, der von <math> 0 </math> verschieden ist, ist der größte gemeinsame Teiler von <math> a </math> und <math> b </math>. | ||
{| class="wikitable mw-collapsible" | {| class="wikitable mw-collapsible" | ||
|+Beispiel | |+Beispiel | ||
| − | !Gesucht ist der ggT von 22 und 16 | + | !Gesucht ist der <math> ggT </math> von <math> a = 22 </math> und <math> b = 16 </math> |
|- | |- | ||
| − | |1. 22 | + | |1. <math> \frac{a}{b} = \frac{22}{16} = 1 \hspace{10pt} \text{Rest} \hspace{5pt} 6 = r </math> |
| − | 2. Rest ungleich 0 | + | |
| + | 2. Rest ungleich <math> 0 \Rightarrow </math> Schritt 1 | ||
| − | 3. 16 | + | 3. <math> \frac{b}{r} = \frac{16}{6} = 2 \hspace{10pt} \text{Rest} \hspace{5pt} 4 = s </math> |
| − | 4. 6 | + | 4. <math> \frac{r}{s} = \frac{6}{4} = 1 \hspace{13pt} \text{Rest} \hspace{5pt} 2 = t </math> |
| − | 5. 4 | + | 5. <math> \frac{s}{t} = \frac{4}{2} = 2 \hspace{13pt} \text{Rest} \hspace{5pt} 0 </math> |
| − | + | <math> \Rightarrow </math> Der größte gemeinsame Teiler von <math> 22 </math> und <math> 16 </math> ist <math> 2 </math>. | |
|} | |} | ||
| − | = | + | =Was sind Kettenbrüche?<ref name="Endliche Kettenbrüche">[https://www.mathematik.tu-dortmund.de/sites/seminar-zur-algebra-und-zahlentheorie-ws-19-20/download/Ausarbeitung3.pdf Johannes Klee: Endliche Kettenbrüche (2019)], Masterseminar WiSe 19/20 an der TU Dortmund </ref>= |
| − | <b>Satz:</b> Eine reelle Zahl ist genau dann rational, wenn sie sich als endlichen Kettenbruch darstellen lässt. | + | |
| + | Bevor nun ein Zusammenhang zwischen dem Euklidischen Algorithmus und Kettenbrüchen hergestellt werden kann, sollten zuerst ein paar Grundlegende Konzepte mit Notation eingeführt | ||
| + | werden. | ||
| + | |||
| + | Ein (unendlicher<sup>(1)</sup>/endlicher<sup>(2)</sup>) <b>Kettenbruch</b> ist generell ein Ausdruck der Form: | ||
| + | |||
| + | <math> \hspace{10pt} </math> | ||
| + | <math> a_0 + \dfrac{b_1}{a_1 + \dfrac{b_2}{a_2 + \dfrac{b_3}{ \hspace{10pt} \ddots }}} \hspace{12pt} (1) </math> | ||
| + | <math> \hspace{10pt} </math> oder <math> \hspace{10pt} </math> | ||
| + | <math> a_0 + \dfrac{b_1}{a_1 + \dfrac{b_2}{ a_{n-2} + \dfrac{\ddots}{ \hspace{10pt} a_{n-1} + \dfrac{b_n}{a_n}}}} \hspace{12pt} (2) </math> | ||
| + | <math> \hspace{10pt} </math> | ||
| + | <math> \hspace{10pt} </math> mit <math> \hspace{20pt} a_i, b_j \in \mathbb{Z} \hspace{5pt} </math> für <math> \hspace{5pt} i \in \mathbb{N}_0 \hspace{5pt} </math> und <math> \hspace{5pt} j \in \mathbb{N}. </math> | ||
| + | |||
| + | In unseren Beispielen reicht es jedoch aus, lediglich <b> reguläre </b> Kettenbrüche zu betrachten. Diese haben die Form: | ||
| + | |||
| + | <math> \hspace{10pt} </math> | ||
| + | <math> a_0 + \dfrac{1}{a_1 + \dfrac{1}{a_2 + \dfrac{1}{ \hspace{10pt} \ddots }}} \hspace{12pt} (a) </math> | ||
| + | <math> \hspace{10pt} </math> oder <math> \hspace{10pt} </math> | ||
| + | <math> a_0 + \dfrac{1}{a_1 + \dfrac{1}{ a_{n-2} + \dfrac{\ddots}{ \hspace{10pt} a_{n-1} + \dfrac{1}{a_n}}}} \hspace{12pt} (b) </math> | ||
| + | <math> \hspace{10pt} </math> | ||
| + | <math> \hspace{10pt} </math> mit <math> \hspace{20pt} a_0 \in \mathbb{Z} \hspace{5pt} </math> und <math> \hspace{5pt} a_i \in \mathbb{N} \hspace{5pt} </math> für <math> \hspace{5pt} i \in \mathbb{N}. </math> | ||
| + | |||
| + | Wie man erkennen kann, ist ein regulärer Kettenbruch somit durch seine Koeffizienten <math> a_0 </math> und <math> a_i </math> eindeutig gegeben. Die gängige | ||
| + | Notation für diese Art von Kettenbruch ist wie folgt: | ||
| + | |||
| + | :<math> (a): \hspace{12pt} \left< a_0; a_1, a_2, \dots \right> </math> | ||
| + | |||
| + | :<math> (b): \hspace{13pt} \left< a_0; a_1, a_2, \dots, a_n \right> </math> | ||
| + | |||
| + | <br> | ||
| + | |||
| + | Zusätzlich lässt sich im (un-)endlichen Fall auch der <b>Abschnitt</b> oder <b>Partialbruch</b> | ||
| + | des Kettenbruchs definieren. Für <math> 0 \le k \le n </math> (endlich) bzw. <math> k \ge 0 </math> (unendlich) | ||
| + | definiert man: | ||
| + | |||
| + | $$ s_k := \left< a_0; a_1, a_2, \dots, a_k \right> $$ | ||
| + | |||
| + | mit dazugehörigem <math> \text{Rest} </math> : | ||
| + | |||
| + | $$ r_k := \left< a_k; a_{k+1}, a_{k+2}, \dots, a_n \right> | ||
| + | \hspace{20pt} | ||
| + | \text{bzw.} | ||
| + | \hspace{20pt} | ||
| + | r_k := \left< a_k; a_{k+1}, a_{k+2}, \dots \right> $$ | ||
| + | |||
| + | <math></math> | ||
| + | |||
| + | = Kettenbruchdarstellung rationaler Zahlen <ref name="Endliche Kettenbrüche" /> = | ||
| + | <b>Satz:</b> Eine reelle Zahl ist genau dann rational, wenn sie sich als (regulären) endlichen Kettenbruch darstellen lässt. <br> | ||
| + | Oder äquivalent: Eine reelle Zahl ist genau dann irrational, wenn ihre Kettenbruchdarstellung unendlich ist. | ||
{| class="wikitable left mw-collapsible mw-collapsed font-size: 100%;" | {| class="wikitable left mw-collapsible mw-collapsed font-size: 100%;" | ||
| style="text-align:left; font-size: 100%;" | '''Beweis''' | | style="text-align:left; font-size: 100%;" | '''Beweis''' | ||
|- | |- | ||
| − | | <math> \ | + | | <math> \Leftarrow </math>: Ein endlicher Kettenbruch stellt eine rationale Zahl dar, denn diesen erhält man durch endliche Summen und Produkte im Körper <math> \mathbb{Q} </math>.<br> |
| − | <math> \ | + | <math> \Rightarrow </math>: Dass eine rationale Zahl sich als endlicher Kettenbruch schreiben lässt, ist intuitiv vermutlich einleuchtend. Tatsächlich kann man sogar jede rationale Zahl als regulären endlichen Kettenbruch darstellen. <br> |
Sei <math> p \in \mathbb{Q} </math>, also von der Form <math> \dfrac{k}{l} </math> mit <math> k \in \mathbb{Z}, l \in \mathbb{N} </math>. <br> | Sei <math> p \in \mathbb{Q} </math>, also von der Form <math> \dfrac{k}{l} </math> mit <math> k \in \mathbb{Z}, l \in \mathbb{N} </math>. <br> | ||
'''Schritt 1:''' Setze <math> p_0 = \lfloor p \rfloor \in \mathbb{Z} </math>, ziehe also den ganzzahligen Anteil heraus. Damit entspricht <math> p_0 </math> der eindeutigen ganzen Zahl, für die gilt: <math> k = p_0 \cdot l + r_0 </math> mit <math> 0 \leq r_0 < l </math>. <br> | '''Schritt 1:''' Setze <math> p_0 = \lfloor p \rfloor \in \mathbb{Z} </math>, ziehe also den ganzzahligen Anteil heraus. Damit entspricht <math> p_0 </math> der eindeutigen ganzen Zahl, für die gilt: <math> k = p_0 \cdot l + r_0 </math> mit <math> 0 \leq r_0 < l </math>. <br> | ||
'''Schritt 2:''' | '''Schritt 2:''' | ||
| − | * Fall <math> r_0 > 0 </math>: Es gilt die Gleichung <math> p = p_0 + \dfrac{r_0}{l} = p_0 + \dfrac{1}{\dfrac{l}{r_0}} </math>. Wegen <math> l > r_0 </math> und <math> l, r_0 \in \mathbb{N} </math> folgt <math> p_1 = \lfloor \dfrac{l}{r_0} \rfloor \in \mathbb{N} </math>. Ziehe also wie in Schritt 1 wieder den ganzzahligen Anteil heraus und betrachte die Gleichung <math> l = p_1 \cdot r_0 + r_1 </math> mit <math> 0 \leq r_1 < r_0 </math>. Unterscheide nun wieder die beiden möglichen Fälle <math> r_1 = 0 </math>, dann gilt <math> p = p_0 + \dfrac{1}{p_1} </math>, bzw. <math> r_1 > 0 </math>, dann wiederhole das Vorgehen. Wegen <math> r_0 > r_1 > r_2 > ... \geq 0 </math> und <math> r_0, r_1, r_2, ... \in \mathbb{N} </math> gibt es ein <math> n \in \mathbb{N} </math> mit <math> r_n = 0 </math>. Dann ist die endliche Kettenbruchdarstellung <math> p = p_0 + \dfrac{1}{p_1 + \dfrac{1}{p_2 + \dfrac{1}{p_3 + \dfrac{1}{... + \dfrac{1}{p_n}}}}} </math>. | + | * Fall <math> r_0 > 0 </math>: Es gilt die Gleichung <math> p = p_0 + \dfrac{r_0}{l} = p_0 + \dfrac{1}{\dfrac{l}{r_0}} </math>. Wegen <math> l > r_0 </math> und <math> l, r_0 \in \mathbb{N} </math> folgt <math> p_1 = \lfloor \dfrac{l}{r_0} \rfloor \in \mathbb{N} </math>. Ziehe also wie in Schritt 1 wieder den ganzzahligen Anteil heraus und betrachte die Gleichung <math> l = p_1 \cdot r_0 + r_1 </math> mit <math> 0 \leq r_1 < r_0 </math>. Unterscheide nun wieder die beiden möglichen Fälle <math> r_1 = 0 </math>, dann gilt <math> p = p_0 + \dfrac{1}{p_1} </math>, bzw. <math> r_1 > 0 </math>, dann wiederhole das Vorgehen. Wegen <math> r_0 > r_1 > r_2 > ... \geq 0 </math> und <math> r_0, r_1, r_2, ... \in \mathbb{N}_0 </math> gibt es ein <math> n \in \mathbb{N}_0 </math> mit <math> r_n = 0 </math>. Dann ist die (reguläre) endliche Kettenbruchdarstellung <math> p = p_0 + \dfrac{1}{p_1 + \dfrac{1}{p_2 + \dfrac{1}{p_3 + \dfrac{1}{... + \dfrac{1}{p_n}}}}} </math>. |
* Fall <math> r_0 = 0 </math>: Dann gilt bereits <math> p = p_0 </math> und <math> p </math> besitzt eine endliche Kettenbruchdarstellung. | * Fall <math> r_0 = 0 </math>: Dann gilt bereits <math> p = p_0 </math> und <math> p </math> besitzt eine endliche Kettenbruchdarstellung. | ||
|} | |} | ||
| − | + | == Beispiel == | |
| − | Als Beispiel betrachte <math> p = - \dfrac{ | + | Als Beispiel betrachte <math> p = - \dfrac{75}{27} </math>. <br> |
| − | <math> - | + | Das Vorgehen ist analog zum euklidischen Algorithmus. <br> |
| − | <math> \Rightarrow p = - | + | <math> -75 = -3 \cdot 27 + 6 </math> <br> (Rest 6) <br> |
| − | <math> | + | <math> \Rightarrow p = -3 + \dfrac{6}{27} = -3 + \dfrac{1}{\dfrac{27}{6}} </math> <br> |
| − | <math> \Rightarrow p = - | + | <math> 27 = 4 \cdot 6 + 3 </math> <br> (Rest 3) <br> |
| − | <math> | + | <math> \Rightarrow p = -3 + \dfrac{1}{4 + \dfrac{3}{6}} = -4 + \dfrac{1}{4 + \dfrac{1}{\dfrac{6}{3}}} </math> <br> |
| − | <math> \Rightarrow p = - | + | <math> 6 = 2 \cdot 3 + 0 </math> <br> (Rest 0, also entspricht der vorherige Rest 3 dem <math> ggT(-75, 27) </math> ) <br> |
| + | <math> \Rightarrow p = -3 + \dfrac{1}{4 + \dfrac{1}{2 + \dfrac{0}{3}}} = -3 + \dfrac{1}{4 + \dfrac{1}{2}} </math> <br> | ||
| + | (reguläre, endliche Kettenbruchdarstellung) | ||
| + | |||
| + | == Geometrische Visualisierung von regulären Kettenbrüchen == | ||
| + | |||
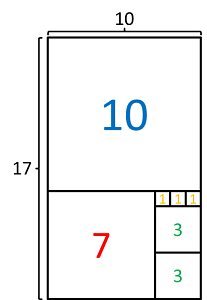
| + | [[Datei:Bild17-10.png|right|thumb|Bruch 1: <math>\frac{17}{10}</math>]] | ||
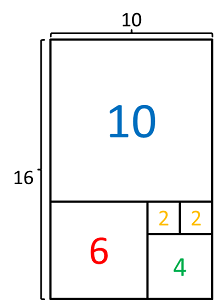
| + | [[Datei:Bild16-10.png|right|thumb|Bruch 2: <math>\frac{16}{10}</math>]] | ||
| + | |||
| + | Der behandelte und bewiesene Algorithmus zum Berechnen der Kettenbruchdarstellung einer rationalen Zahl lässt sich auch visuell darstellen. | ||
| + | Dafür stellt man den zu einer gegebenen Zahl <math> p \in \mathbb{Q} </math> mit <math> p = \frac{k}{l}, \hspace{3pt} k,l \in \mathbb{N} </math> gehörenden Bruch | ||
| + | als Rechteck, mit der Höhe <math> k </math> und der Länge <math> l </math> dar. Zu beachten ist allerdings, dass die Visualisierung nur für positive | ||
| + | Werte von <math> k </math> und <math> l </math> gut funktioniert (negative Seitenlängen ergeben keinen Sinn). | ||
| + | |||
| + | <br> | ||
| + | |||
| + | <b>Dann wird nach folgendem Schema vorgegangen:</b> | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | | | ||
| + | * Fülle das Rechteck soweit möglich mit Quadraten der Seitenlänge <math> l </math> aus. Dies entspricht dem Herausziehen des ganzzahligen Anteils aus einer Zahl. | ||
| + | |||
| + | * Ist das Rechteck noch nicht ausgefüllt, vergleiche die Seitenlängen des übrigen Rechtecks und wähle die kleinere. Fülle nun diese Fläche mit Quadraten der kleineren Seitenlänge soweit möglich aus. Dies entspricht dem herausziehen des ganzzahligen Koeffizienten <math> a_1 </math> auf der zweiten Ebene des Kettenbruchs. <math> a_1 </math> ist dabei die Anzahl der Quadrate. | ||
| + | |||
| + | * Wiederhole den Vorgang so oft, bis das Rechteck komplett ausgefüllt ist. Da dieses Verfahren die direkte graphische Anschauung des Verfahrens zur Gewinnung eines Kettenbruchs aus einer Zahl ist, gelten auch hier die gleichen Abbruchbedingungen wie in obigem Beweis für die Rationalität von endlichen Kettenbrüchen. Der Algotithmus terminiert also genau dann, wenn das Seitenverhältnis des Rechtecks als Bruch ganzer Zahlen geschrieben werden kann. Genauso korreliert diese graphische Anschauung allerdings auch mit dem Euklidischen Algorithmus. Die Seitenlänge des kleinsten Quadrats im Rechteck entspricht nun dem Wert von <math> ggT(k,l) </math> und die Anzahlen der Quadrate mit gleicher Seitenlänge entsprechen (in gleicher Reihenfolge wie bei Anwendung des Schemas) den <math> a_i, \hspace{3pt} i \in \mathbb{N}_0 </math> der regulären Kettenbruchdarstellung von <math> p </math>. | ||
| + | |} | ||
| + | |||
| + | <br> | ||
| + | |||
| + | <b>Beispiel 1:</b> Gegebener Bruch: <math> \dfrac{17}{10} </math><ref name="Bild 1: 17/10">Bild zu 17/10 wurde selbst hergestellt </ref> | ||
| + | |||
| + | <nowiki>$$ \dfrac{17}{10} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{7}{10} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{1}{\dfrac{10}{7}} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{1}{1 + \dfrac{3}{7}} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{1}{1 + \dfrac{1}{\dfrac{7}{3}}} \hspace{10pt} = \hspace{10pt} \color{Blue} 1 + \dfrac{1}{\color{Red} 1 + \dfrac{1}{\color{Green} 2 + \dfrac{1}{\color{Orange} 3}}} $$</nowiki> | ||
| + | |||
| + | <b>Beispiel 2:</b> Gegebener Bruch: <math> \dfrac{16}{10} </math><ref name="Bild 2: 16/10">Bild zu 16/10 wurde selbst hergestellt </ref> | ||
| + | |||
| + | <nowiki>$$ \dfrac{16}{10} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{6}{10} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{1}{\dfrac{10}{6}} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{1}{1 + \dfrac{4}{6}} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{1}{1 + \dfrac{1}{\dfrac{6}{4}}} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{1}{1 + \dfrac{1}{1 + \dfrac{2}{4}}} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{1}{1 + \dfrac{1}{1 + \dfrac{1}{\dfrac{4}{2}}}} \hspace{10pt} = \hspace{10pt} \color{blue} 1 + \dfrac{1}{\color{red} 1 + \dfrac{1}{\color{green} 1 + \dfrac{1}{\color{orange} 2}}} $$</nowiki> | ||
| + | |||
| + | = Kettenbruchdarstellungen irrationaler Zahlen = | ||
| + | Wie im vorigen Abschnitt gezeigt, haben irrationale Zahlen unendliche Kettenbruchdarstellungen. Dabei gilt, dass der Wert eines unendlichen Kettenbruchs der Form <math> \left< a_0; a_1, a_2, \dots \right> </math> festgelegt ist als<ref>[http://www.mathematik.uni-kassel.de/~koepf/Diplome/Scheel.pdf Algorithmen für regelmäßige Kettenbrüche] Stefan Scheel, Bachelorarbeit an der Universität Kassel (2005) </ref> <math> \lim \limits_{n \to \infty} \left< a_0; a_1, \dots, a_n \right> </math>. | ||
| + | Diese Festlegung ist für jeden regulären Kettenbruch sinnvoll, da gilt: | ||
| + | |||
| + | Die Folge der Partialbrüche eines jeden regulären Kettenbruchs konvergiert. | ||
| + | {| class="wikitable mw-collapsible mw-collapsed" | ||
| + | |+Beweis | ||
| + | |Wir definieren für alle <math> n \in \mathbb{N}_0 \\ | ||
| + | K_n := \left< a_0; a_1, a_2, \dots, a_n \right> </math> | ||
| + | des weiteren seien für alle <math> n \in \mathbb{N}_0 \; P_n, Q_n </math> folgendermaßen definiert: | ||
| + | |||
| + | <math> \begin{align} P_0 &:= a_0 \\ | ||
| + | P_1 &:= a_1 a_0 + 1 \\ | ||
| + | P_n &:= a_n P_{n-1} + P_{n-2} \\ \\ | ||
| + | Q_0 &:= 1 \\ | ||
| + | Q_1 &:= a_1 \\ | ||
| + | Q_n &:= a_n Q_{n-1} + Q_{n-2} \end{align} </math> | ||
| + | |||
| + | Nun lässt sich induktiv zeigen, dass für alle <math> n \in \mathbb{N}_0 </math> gilt <math> K_n = \dfrac{P_n}{Q_n} </math> | ||
| + | |||
| + | Induktionsanfang: | ||
| + | <math> K_0 = a_0 = \dfrac{P_0}{Q_0} </math> | ||
| + | |||
| + | Induktionsschritt <math> (n \rightarrow n+1) </math>: | ||
| + | |||
| + | <math> \begin{align} K_{n+1} &= \left< a_0; a_1, a_2, \dots, a_{n+1} \right> \\ \\ | ||
| + | &=\left< a_0; a_1, a_2, \dots, a_n + \dfrac{1}{a_{n+1}} \right> \\ \\ | ||
| + | &= \dfrac{(a_n +\dfrac{1}{a_{n+1}})P_{k-1} + P_{k-2}}{(a_n+\dfrac{1}{a_{n+1}})Q_{n-1} + Q_{n-2}} \\ \\ | ||
| + | &= \dfrac{a_{n+1} (a_n P_{n-1} + P_{n-2} )+P_{n-1} }{a_{n+1} (a_n Q_{n-1} + Q_{n-2} )+Q_{n-1} } \\ \\ | ||
| + | &= \dfrac{a_{n+1} P_n +P_{n-1} }{a_{n+1} Q_n +Q_{n-1} } \\ \\ | ||
| + | &= \dfrac{P_{n+1}}{Q_{n+1}} \end{align} </math> | ||
| + | |||
| + | Aus dieser Formel lässt sich für alle <math> k \in \mathbb{N} </math> schließen | ||
| + | |||
| + | <math> \begin{align} K_{2k}-K_{2k-2} &= (K_{k+2}-K_{k+1})+(K_{k+1}-K_{k}) \\ \\ | ||
| + | &= (\dfrac{P_{k+2}}{Q_{k+2}}-\dfrac{P_{k+1}}{Q_{k+1}}) + (\dfrac{P_{k+1}}{Q_{k+1}}-\dfrac{P_{k}}{Q_{k}}) \\ | ||
| + | &=\dfrac{(-1)^{k+1}}{Q_{k+2}Q_{k+1}}+ \dfrac{(-1)^k}{Q_{k+1}Q_k} \\ \\ | ||
| + | &= \dfrac{(-1)^k(Q_{k+2}-Q_k)}{Q_{k+2}Q_{k+1}Q_k} \end{align} </math> | ||
| + | |||
| + | Nun gilt für alle <math> k \; \; Q_{k+2}-Q_{k} > 0 </math> | ||
| + | <math> \Rightarrow K_0 < K_2 < K_4 \dots </math> und <math> K_1 > K_3 > K_5 \dots </math> | ||
| + | Da die Folge der Partialbrüche nach unten durch <math> a_0 </math> und nach oben durch <math> a_0+1 </math> beschränkt ist, wissen wir | ||
| + | nun, dass die Teilfolge der Partialbrüche mit geraden Indizes und die der Partialbrüche mit ungeraden Indizes konvergieren. Es bleibt | ||
| + | also nur noch zu zeigen, dass beide Teilfolgen gegen den selben Wert konvergieren. | ||
| − | = | + | Dazu seien <math> \alpha := \lim \limits_{n \to \infty} K_{2n}, \; \alpha´ := \lim \limits_{n \to \infty} K_{2n-1} </math> |
| − | + | Aufgrund von <math> K_{k+1}-K_{k} = \dfrac{(-1)^k}{Q_{k+1}Q_k}, \; k \in \mathbb{N} </math> (siehe oben), | |
| + | gilt <math> \alpha ≥ \alpha´ </math>. | ||
| − | <math> | + | Des weiteren gilt <math> K_{2n} < \alpha, \; K_{2n+1} > \alpha´ \\ |
| − | + | \Rightarrow \alpha - \alpha´ < K_{2n+1}-K_{2n} = \dfrac{(-1)^{2n}}{Q_{2n+1}Q_{2n}} = \dfrac{1}{Q_{2n+1}Q_{2n}}, \; n \in \mathbb{N} </math> | |
| − | |||
| − | + | Da <math> Q_n </math> seiner Bildungsvorschrift nach für genügend große <math> n </math> beliebig groß wird, gilt also | |
| − | = | + | <math> \alpha ≤ \alpha´ \Rightarrow \alpha = \alpha´ \\ |
| + | \Rightarrow \lim \limits_{n \to \infty} \left< a_0; a_1, \dots, a_n \right> = \lim \limits_{n \to \infty} K_{n} = \alpha </math> | ||
| + | |} | ||
== Beweis für die Irrationalität von <math> \sqrt{10} </math> == | == Beweis für die Irrationalität von <math> \sqrt{10} </math> == | ||
| − | Wir wissen, dass eine Zahl genau dann | + | Wir wissen, dass eine Zahl genau dann rational ist, wenn ihre Kettenbruchdarstellung endlich ist. Daher können wir zeigen, ob eine Zahl rational ist, indem wir ihre Kettenbruchdarstellung berechnen. |
<math> \begin{align} \sqrt{10} &= 3 + (\sqrt{10} - 3) = 3 + \dfrac{(\sqrt{10} - 3)(\sqrt{10} + 3)}{3 + \sqrt{10}} = 3 + \dfrac{1}{3 + \sqrt{10}} \\ \\ | <math> \begin{align} \sqrt{10} &= 3 + (\sqrt{10} - 3) = 3 + \dfrac{(\sqrt{10} - 3)(\sqrt{10} + 3)}{3 + \sqrt{10}} = 3 + \dfrac{1}{3 + \sqrt{10}} \\ \\ | ||
| Zeile 89: | Zeile 228: | ||
Diese Darstellung bricht nie ab; <math> \sqrt{10} </math> ist demnach irrational. | Diese Darstellung bricht nie ab; <math> \sqrt{10} </math> ist demnach irrational. | ||
| − | ==Berechnung des Wertes eines periodischen Kettenbruchs== | + | ==Berechnung des Wertes eines periodischen Kettenbruchs<ref>[https://www.mathematik.tu-dortmund.de/sites/seminar-zur-algebra-und-zahlentheorie-ws-19-20/download/Ausarbeitung8.pdf Thomas Boecker: Periodische Kettenbrüche] Seminar zur Algebra und Zahlentheorie, WiSe 19/20 an der TU Dortmund </ref>== |
Sei <math> \xi </math> eine reelle Zahl gegeben durch <math> \: \xi := 4 + \dfrac{1}{1+\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{2+\dfrac{1}{\hspace{10pt} \ddots}}}}}}} </math> | Sei <math> \xi </math> eine reelle Zahl gegeben durch <math> \: \xi := 4 + \dfrac{1}{1+\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{2+\dfrac{1}{\hspace{10pt} \ddots}}}}}}} </math> | ||
| Zeile 99: | Zeile 238: | ||
| − | Da dieser Kettenbruch aber periodisch ist, können wir auch den exakten Wert von <math> \xi </math> berechnen. Dazu definieren wir | + | Da dieser Kettenbruch aber periodisch ist, können wir auch den exakten Wert von <math> \xi. </math> berechnen. Dazu definieren wir |
<math> \theta := 2+\dfrac{1}{3+\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{2+\dfrac{1}{\hspace{10pt} \ddots}}}}} </math> | <math> \theta := 2+\dfrac{1}{3+\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{2+\dfrac{1}{\hspace{10pt} \ddots}}}}} </math> | ||
| Zeile 115: | Zeile 254: | ||
= \dfrac{29 + \sqrt{15}}{7} </math> | = \dfrac{29 + \sqrt{15}}{7} </math> | ||
| − | ==Kettenbruchdarstellung von <math> \pi </math>== | + | Wie in dieser Beispielrechnung zu sehen, ist der Wert eines jeden rein periodischen Kettenbruchs die irrationale Lösung eines quadratischen Polynoms mit rationalen Koeffizienten, eine so genannte quadratische Irrationalzahl. Tatsächlich lässt sich aber noch mehr zeigen. |
| + | |||
| + | '''Satz von Euler-Lagrange:''' Jeder periodische Kettenbruch ist eine quadratische Irrationalzahl und umgekehrt. | ||
| + | |||
| + | ==Kettenbruchdarstellung von <math> \pi </math><ref>[https://faculty.math.illinois.edu/~hildebr/453.spring11/pi-cf.pdf Continued Fraction Approximations to <math> \pi </math>] University of Illinois - Department of Mathematics </ref>== | ||
| + | |||
| + | Da wir den ungefähren Wert von <math> \pi </math> kennen, können wir es als regulären Kettenbruch entwickeln. Sei dazu <math> \left< a_0; a_1, a_2, \dots \right> := \pi </math> | ||
| + | |||
| + | Es gilt | ||
| + | |||
| + | <math> 3< \pi < 4 \Rightarrow a_0 = 3 \\ | ||
| + | \pi=3+(\pi-3) \; \; \; \; \dfrac{1}{8} < \pi-3 < \dfrac{1}{7} \Rightarrow a_1 = 7 \\ | ||
| + | \pi=3+\dfrac{1}{7+(\dfrac{1}{\pi-3}-7)} \; \; \; \; \dfrac{1}{16} < \dfrac{1}{\pi-3}-7 < \dfrac{1}{15} \Rightarrow a_2 = 15 \\ \dots \\ </math> | ||
| − | <math> \pi = 3+\dfrac{1}{7+\dfrac{1}{15+\dfrac{1}{1+\dfrac{1}{292+\dfrac{1}{1+{\dfrac{1}{\hspace{10pt} \ddots}}}}}}} </math> | + | <math> \pi</math><math> = 3+\dfrac{1}{7+\dfrac{1}{15+\dfrac{1}{1+\dfrac{1}{292+\dfrac{1}{1+{\dfrac{1}{\hspace{10pt} \ddots}}}}}}} </math> |
| − | + | Werten wir die Partialbrüche dieses Kettenbruchs aus, sehen wir, dass sie eine gute Annäherung an <math> \pi </math> liefern. | |
| − | {| class="wikitable" | + | {| class="wikitable mw-collapsible" |
|+ | |+ | ||
| − | ! colspan="3" |<math> \begin{align} \pi &= 3.1415926535897932384626433832795028... \\ &= | + | ! colspan="3" |<math> \begin{align} \pi &= 3.1415926535897932384626433832795028... \\ &= \left<3;7,15,1,292,1,1,1,2,1,3,1,14,2,1,1,...\right> \end{align} </math> |
|- | |- | ||
!Partialbruch | !Partialbruch | ||
| Zeile 128: | Zeile 279: | ||
!Wert als Dezimalzahl | !Wert als Dezimalzahl | ||
|- | |- | ||
| − | | | + | |<math> \left<3\right></math> |
| − | | <math> | + | | <math> \dfrac{3}{1} </math> |
|'''3.'''00000000000000... | |'''3.'''00000000000000... | ||
|- | |- | ||
| − | | | + | |<math>\left<3;7\right></math> |
| − | |<math> \dfrac{22}{7} </math> | + | | <math>\dfrac{22}{7} </math> |
|'''3.14'''285714285714... | |'''3.14'''285714285714... | ||
|- | |- | ||
| − | | | + | |<math>\left<3;7,15\right></math> |
| − | |<math> \dfrac{333}{106} </math> | + | | <math>\dfrac{333}{106} </math> |
|'''3.1415'''0943396226... | |'''3.1415'''0943396226... | ||
|- | |- | ||
| − | | | + | |<math>\left<3;7,15,1\right></math> |
| − | |<math> \dfrac{355}{113} </math> | + | |<math>\dfrac{355}{113} </math> |
|'''3.141592'''92035398... | |'''3.141592'''92035398... | ||
|- | |- | ||
| − | | | + | |<math>\left<3;7,15,1,292\right></math> |
| − | |<math> \dfrac{103993}{33102} </math> | + | | <math>\dfrac{103993}{33102} </math> |
|'''3.141592653'''01190... | |'''3.141592653'''01190... | ||
|- | |- | ||
| − | | | + | |<math>\left<3;7,15,1,292,1\right></math> |
| − | |<math> \dfrac{104348}{33215} </math> | + | |<math>\dfrac{104348}{33215}</math> |
|'''3.141592653'''92142... | |'''3.141592653'''92142... | ||
|- | |- | ||
| − | | | + | |<math>\left<3;7,15,1,292,1,1\right></math> |
| − | |<math> \dfrac{208341}{66317} </math> | + | |<math>\dfrac{208341}{66317} </math> |
|'''3.141592653'''46744... | |'''3.141592653'''46744... | ||
|- | |- | ||
| − | | | + | |<math>\left<3;7,15,1,292,1,1,1\right></math> |
| − | |<math> \dfrac{312689}{99532} </math> | + | |<math>\dfrac{312689}{99532} </math> |
|'''3.141592653'''61894... | |'''3.141592653'''61894... | ||
|- | |- | ||
| − | | | + | |<math>\left<3;7,15,1,292,1,1,1,2\right></math> |
| − | |<math> \dfrac{833719}{265381} </math> | + | | <math>\dfrac{833719}{265381} </math> |
| − | |'''3.14159265358'''108... | + | |'''3.14159265358'''108... |
|} | |} | ||
| − | + | Da <math> \pi </math> irrational ist und bisher keine Muster in dessen regulärem Kettenbruch gefunden wurden, können wir nur endliche Partialbrüche von diesem berechnen. Wenn wir uns aber nicht auf reguläre Kettenbrüche beschränken, gibt es Kettenbrüche von <math> \pi </math>, die Muster enthalten.<ref>[https://www.math.uni-sb.de/ag/gekeler/PERSONEN/Bachelorarbeiten/Stopp.pdf Zur Arithmetik von Kettenbrüchen] Philipp Stopp, Bachelorarbeit vorgelegt der Mathematisch-Naturwissenschaftlichen Fakultät der Universität des Saarlandes (2009) </ref> | |
| − | + | ||
| + | So zeigte Johann Heinrich Lambert: | ||
| + | |||
| + | <math> \dfrac{4}{\pi}=1+\dfrac{1^2}{3+\dfrac{2^2}{5+\dfrac{3^2}{7+\dfrac{4^2}{9+\dfrac{5^2}{11+\dfrac{6^2}{\hspace{10pt} \ddots}}}}}} </math> | ||
| − | <math> \ | + | Von Leonhard Euler stammt die Entwicklung: |
| + | |||
| + | <math> \pi= 1+\dfrac{1^2}{6+\dfrac{3^2}{6+\dfrac{5^2}{6+\dfrac{7^2}{6+\dfrac{9^2}{6+\dfrac{11^2}{\hspace{10pt} \ddots}}}}}} </math> | ||
| + | |||
| + | =Siehe auch= | ||
| + | * [[Goldener Schnitt]] | ||
| + | * [[Riemannsche Vermutung]] | ||
| + | * [[Pi und das Buffon'sche Nadelproblem]] | ||
| + | |||
| + | =Einzelnachweise= | ||
<references /> | <references /> | ||
| + | |||
| + | =Autoren= | ||
| + | * Victoria Mezger | ||
| + | * Pirmin Kupffer | ||
| + | * Marvin Hertweck | ||
| + | * Paul Bruckert | ||
Aktuelle Version vom 15. April 2021, 08:00 Uhr
Diese Seite behandelt den simplen, aber zugleich genialen Euklidischen Algorithmus und wie dieser mit der Kettenbruchdarstellung rationaler und irrationaler Zahlen zusammenhängt.
Der Euklidische Algorithmus
Schon 300 vor Christus befasste sich Euklid in seinem berühmten Werk "Die Elemente" mit der Frage, wie man das größte gemeinsame Maß, also den größten gemeinsamen Teiler ([math] ggT [/math]) zweier Zahlen finden kann.
Er entwickelte dazu einen Algorithmus, der auf folgendem Lemma beruht:
Lemma: Es seien [math] a, b, q, r \in \mathbb{N} [/math] und [math] b \gt 0 [/math] mit
- [math] a = bq + r, \hspace{20pt} 0 \le r \lt b [/math]
Dann gilt:[math] \hspace{10pt} ggT(a, b) = ggT(b, r). [/math]
| Es gilt [math] a = bq + r [/math], also ist jeder gemeinsame Teiler von [math] b [/math] und [math] r [/math] auch ein Teiler von
[math] a [/math]. Stellt man die Gleichung nach [math] r [/math] um, erhält man [math] r = a - bq [/math] und somit ist jeder gemeinsame Teiler von [math] a [/math] und [math] b [/math] auch ein Teiler von [math] r [/math]. Die Zahlenpaare [math] (a, b) [/math] und [math] (b, r) [/math] haben also die gleichen gemeinsamen Teiler und somit auch den gleichen [math] ggT [/math]. |
Funktionsweise
Gesucht ist nun der größte gemeinsame Teiler zweier ganzer Zahlen [math] a [/math] und [math] b [/math] mit [math] a \gt b [/math]. Der Algorithmus funktioniert wie folgt:
- Teile [math] a [/math] durch [math] b [/math] und erhalten den Rest [math] r [/math].
- Ist [math] r = 0 [/math], ist [math] a [/math] ohne Rest durch [math] b [/math] teilbar und es gilt [math] ggT(a, b) = b [/math].
- Ist [math] r \neq 0 [/math], führe Schritt 1 für [math] b [/math] und [math] r [/math] durch.
- Führe die Schritte solange durch, bis Rest [math] 0 [/math] bleibt. Dann lässt sich die Zahl als Produkt zweier anderer natürlicher Zahlen schreiben und es gilt:
Der letzte Rest, der von [math] 0 [/math] verschieden ist, ist der größte gemeinsame Teiler von [math] a [/math] und [math] b [/math].
| Gesucht ist der [math] ggT [/math] von [math] a = 22 [/math] und [math] b = 16 [/math] |
|---|
| 1. [math] \frac{a}{b} = \frac{22}{16} = 1 \hspace{10pt} \text{Rest} \hspace{5pt} 6 = r [/math]
2. Rest ungleich [math] 0 \Rightarrow [/math] Schritt 1 3. [math] \frac{b}{r} = \frac{16}{6} = 2 \hspace{10pt} \text{Rest} \hspace{5pt} 4 = s [/math] 4. [math] \frac{r}{s} = \frac{6}{4} = 1 \hspace{13pt} \text{Rest} \hspace{5pt} 2 = t [/math] 5. [math] \frac{s}{t} = \frac{4}{2} = 2 \hspace{13pt} \text{Rest} \hspace{5pt} 0 [/math] [math] \Rightarrow [/math] Der größte gemeinsame Teiler von [math] 22 [/math] und [math] 16 [/math] ist [math] 2 [/math]. |
Was sind Kettenbrüche?[1]
Bevor nun ein Zusammenhang zwischen dem Euklidischen Algorithmus und Kettenbrüchen hergestellt werden kann, sollten zuerst ein paar Grundlegende Konzepte mit Notation eingeführt werden.
Ein (unendlicher(1)/endlicher(2)) Kettenbruch ist generell ein Ausdruck der Form:
[math] \hspace{10pt} [/math] [math] a_0 + \dfrac{b_1}{a_1 + \dfrac{b_2}{a_2 + \dfrac{b_3}{ \hspace{10pt} \ddots }}} \hspace{12pt} (1) [/math] [math] \hspace{10pt} [/math] oder [math] \hspace{10pt} [/math] [math] a_0 + \dfrac{b_1}{a_1 + \dfrac{b_2}{ a_{n-2} + \dfrac{\ddots}{ \hspace{10pt} a_{n-1} + \dfrac{b_n}{a_n}}}} \hspace{12pt} (2) [/math] [math] \hspace{10pt} [/math] [math] \hspace{10pt} [/math] mit [math] \hspace{20pt} a_i, b_j \in \mathbb{Z} \hspace{5pt} [/math] für [math] \hspace{5pt} i \in \mathbb{N}_0 \hspace{5pt} [/math] und [math] \hspace{5pt} j \in \mathbb{N}. [/math]
In unseren Beispielen reicht es jedoch aus, lediglich reguläre Kettenbrüche zu betrachten. Diese haben die Form:
[math] \hspace{10pt} [/math] [math] a_0 + \dfrac{1}{a_1 + \dfrac{1}{a_2 + \dfrac{1}{ \hspace{10pt} \ddots }}} \hspace{12pt} (a) [/math] [math] \hspace{10pt} [/math] oder [math] \hspace{10pt} [/math] [math] a_0 + \dfrac{1}{a_1 + \dfrac{1}{ a_{n-2} + \dfrac{\ddots}{ \hspace{10pt} a_{n-1} + \dfrac{1}{a_n}}}} \hspace{12pt} (b) [/math] [math] \hspace{10pt} [/math] [math] \hspace{10pt} [/math] mit [math] \hspace{20pt} a_0 \in \mathbb{Z} \hspace{5pt} [/math] und [math] \hspace{5pt} a_i \in \mathbb{N} \hspace{5pt} [/math] für [math] \hspace{5pt} i \in \mathbb{N}. [/math]
Wie man erkennen kann, ist ein regulärer Kettenbruch somit durch seine Koeffizienten [math] a_0 [/math] und [math] a_i [/math] eindeutig gegeben. Die gängige Notation für diese Art von Kettenbruch ist wie folgt:
- [math] (a): \hspace{12pt} \left\lt a_0; a_1, a_2, \dots \right\gt [/math]
- [math] (b): \hspace{13pt} \left\lt a_0; a_1, a_2, \dots, a_n \right\gt [/math]
Zusätzlich lässt sich im (un-)endlichen Fall auch der Abschnitt oder Partialbruch des Kettenbruchs definieren. Für [math] 0 \le k \le n [/math] (endlich) bzw. [math] k \ge 0 [/math] (unendlich) definiert man:
$$ s_k := \left< a_0; a_1, a_2, \dots, a_k \right> $$
mit dazugehörigem [math] \text{Rest} [/math] :
$$ r_k := \left< a_k; a_{k+1}, a_{k+2}, \dots, a_n \right> \hspace{20pt} \text{bzw.} \hspace{20pt} r_k := \left< a_k; a_{k+1}, a_{k+2}, \dots \right> $$
[math][/math]
Kettenbruchdarstellung rationaler Zahlen [1]
Satz: Eine reelle Zahl ist genau dann rational, wenn sie sich als (regulären) endlichen Kettenbruch darstellen lässt.
Oder äquivalent: Eine reelle Zahl ist genau dann irrational, wenn ihre Kettenbruchdarstellung unendlich ist.
| Beweis |
| [math] \Leftarrow [/math]: Ein endlicher Kettenbruch stellt eine rationale Zahl dar, denn diesen erhält man durch endliche Summen und Produkte im Körper [math] \mathbb{Q} [/math]. [math] \Rightarrow [/math]: Dass eine rationale Zahl sich als endlicher Kettenbruch schreiben lässt, ist intuitiv vermutlich einleuchtend. Tatsächlich kann man sogar jede rationale Zahl als regulären endlichen Kettenbruch darstellen.
|
Beispiel
Als Beispiel betrachte [math] p = - \dfrac{75}{27} [/math].
Das Vorgehen ist analog zum euklidischen Algorithmus.
[math] -75 = -3 \cdot 27 + 6 [/math]
(Rest 6)
[math] \Rightarrow p = -3 + \dfrac{6}{27} = -3 + \dfrac{1}{\dfrac{27}{6}} [/math]
[math] 27 = 4 \cdot 6 + 3 [/math]
(Rest 3)
[math] \Rightarrow p = -3 + \dfrac{1}{4 + \dfrac{3}{6}} = -4 + \dfrac{1}{4 + \dfrac{1}{\dfrac{6}{3}}} [/math]
[math] 6 = 2 \cdot 3 + 0 [/math]
(Rest 0, also entspricht der vorherige Rest 3 dem [math] ggT(-75, 27) [/math] )
[math] \Rightarrow p = -3 + \dfrac{1}{4 + \dfrac{1}{2 + \dfrac{0}{3}}} = -3 + \dfrac{1}{4 + \dfrac{1}{2}} [/math]
(reguläre, endliche Kettenbruchdarstellung)
Geometrische Visualisierung von regulären Kettenbrüchen
Der behandelte und bewiesene Algorithmus zum Berechnen der Kettenbruchdarstellung einer rationalen Zahl lässt sich auch visuell darstellen. Dafür stellt man den zu einer gegebenen Zahl [math] p \in \mathbb{Q} [/math] mit [math] p = \frac{k}{l}, \hspace{3pt} k,l \in \mathbb{N} [/math] gehörenden Bruch als Rechteck, mit der Höhe [math] k [/math] und der Länge [math] l [/math] dar. Zu beachten ist allerdings, dass die Visualisierung nur für positive Werte von [math] k [/math] und [math] l [/math] gut funktioniert (negative Seitenlängen ergeben keinen Sinn).
Dann wird nach folgendem Schema vorgegangen:
|
Beispiel 1: Gegebener Bruch: [math] \dfrac{17}{10} [/math][2]
$$ \dfrac{17}{10} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{7}{10} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{1}{\dfrac{10}{7}} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{1}{1 + \dfrac{3}{7}} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{1}{1 + \dfrac{1}{\dfrac{7}{3}}} \hspace{10pt} = \hspace{10pt} \color{Blue} 1 + \dfrac{1}{\color{Red} 1 + \dfrac{1}{\color{Green} 2 + \dfrac{1}{\color{Orange} 3}}} $$
Beispiel 2: Gegebener Bruch: [math] \dfrac{16}{10} [/math][3]
$$ \dfrac{16}{10} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{6}{10} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{1}{\dfrac{10}{6}} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{1}{1 + \dfrac{4}{6}} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{1}{1 + \dfrac{1}{\dfrac{6}{4}}} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{1}{1 + \dfrac{1}{1 + \dfrac{2}{4}}} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{1}{1 + \dfrac{1}{1 + \dfrac{1}{\dfrac{4}{2}}}} \hspace{10pt} = \hspace{10pt} \color{blue} 1 + \dfrac{1}{\color{red} 1 + \dfrac{1}{\color{green} 1 + \dfrac{1}{\color{orange} 2}}} $$
Kettenbruchdarstellungen irrationaler Zahlen
Wie im vorigen Abschnitt gezeigt, haben irrationale Zahlen unendliche Kettenbruchdarstellungen. Dabei gilt, dass der Wert eines unendlichen Kettenbruchs der Form [math] \left\lt a_0; a_1, a_2, \dots \right\gt [/math] festgelegt ist als[4] [math] \lim \limits_{n \to \infty} \left\lt a_0; a_1, \dots, a_n \right\gt [/math]. Diese Festlegung ist für jeden regulären Kettenbruch sinnvoll, da gilt:
Die Folge der Partialbrüche eines jeden regulären Kettenbruchs konvergiert.
| Wir definieren für alle [math] n \in \mathbb{N}_0 \\
K_n := \left\lt a_0; a_1, a_2, \dots, a_n \right\gt [/math]
des weiteren seien für alle [math] n \in \mathbb{N}_0 \; P_n, Q_n [/math] folgendermaßen definiert: [math] \begin{align} P_0 &:= a_0 \\ P_1 &:= a_1 a_0 + 1 \\ P_n &:= a_n P_{n-1} + P_{n-2} \\ \\ Q_0 &:= 1 \\ Q_1 &:= a_1 \\ Q_n &:= a_n Q_{n-1} + Q_{n-2} \end{align} [/math] Nun lässt sich induktiv zeigen, dass für alle [math] n \in \mathbb{N}_0 [/math] gilt [math] K_n = \dfrac{P_n}{Q_n} [/math] Induktionsanfang: [math] K_0 = a_0 = \dfrac{P_0}{Q_0} [/math] Induktionsschritt [math] (n \rightarrow n+1) [/math]: [math] \begin{align} K_{n+1} &= \left\lt a_0; a_1, a_2, \dots, a_{n+1} \right\gt \\ \\ &=\left\lt a_0; a_1, a_2, \dots, a_n + \dfrac{1}{a_{n+1}} \right\gt \\ \\ &= \dfrac{(a_n +\dfrac{1}{a_{n+1}})P_{k-1} + P_{k-2}}{(a_n+\dfrac{1}{a_{n+1}})Q_{n-1} + Q_{n-2}} \\ \\ &= \dfrac{a_{n+1} (a_n P_{n-1} + P_{n-2} )+P_{n-1} }{a_{n+1} (a_n Q_{n-1} + Q_{n-2} )+Q_{n-1} } \\ \\ &= \dfrac{a_{n+1} P_n +P_{n-1} }{a_{n+1} Q_n +Q_{n-1} } \\ \\ &= \dfrac{P_{n+1}}{Q_{n+1}} \end{align} [/math] Aus dieser Formel lässt sich für alle [math] k \in \mathbb{N} [/math] schließen [math] \begin{align} K_{2k}-K_{2k-2} &= (K_{k+2}-K_{k+1})+(K_{k+1}-K_{k}) \\ \\ &= (\dfrac{P_{k+2}}{Q_{k+2}}-\dfrac{P_{k+1}}{Q_{k+1}}) + (\dfrac{P_{k+1}}{Q_{k+1}}-\dfrac{P_{k}}{Q_{k}}) \\ &=\dfrac{(-1)^{k+1}}{Q_{k+2}Q_{k+1}}+ \dfrac{(-1)^k}{Q_{k+1}Q_k} \\ \\ &= \dfrac{(-1)^k(Q_{k+2}-Q_k)}{Q_{k+2}Q_{k+1}Q_k} \end{align} [/math] Nun gilt für alle [math] k \; \; Q_{k+2}-Q_{k} \gt 0 [/math] [math] \Rightarrow K_0 \lt K_2 \lt K_4 \dots [/math] und [math] K_1 \gt K_3 \gt K_5 \dots [/math] Da die Folge der Partialbrüche nach unten durch [math] a_0 [/math] und nach oben durch [math] a_0+1 [/math] beschränkt ist, wissen wir nun, dass die Teilfolge der Partialbrüche mit geraden Indizes und die der Partialbrüche mit ungeraden Indizes konvergieren. Es bleibt also nur noch zu zeigen, dass beide Teilfolgen gegen den selben Wert konvergieren. Dazu seien [math] \alpha := \lim \limits_{n \to \infty} K_{2n}, \; \alpha´ := \lim \limits_{n \to \infty} K_{2n-1} [/math] Aufgrund von [math] K_{k+1}-K_{k} = \dfrac{(-1)^k}{Q_{k+1}Q_k}, \; k \in \mathbb{N} [/math] (siehe oben), gilt [math] \alpha ≥ \alpha´ [/math]. Des weiteren gilt [math] K_{2n} \lt \alpha, \; K_{2n+1} \gt \alpha´ \\ \Rightarrow \alpha - \alpha´ \lt K_{2n+1}-K_{2n} = \dfrac{(-1)^{2n}}{Q_{2n+1}Q_{2n}} = \dfrac{1}{Q_{2n+1}Q_{2n}}, \; n \in \mathbb{N} [/math] Da [math] Q_n [/math] seiner Bildungsvorschrift nach für genügend große [math] n [/math] beliebig groß wird, gilt also [math] \alpha ≤ \alpha´ \Rightarrow \alpha = \alpha´ \\ \Rightarrow \lim \limits_{n \to \infty} \left\lt a_0; a_1, \dots, a_n \right\gt = \lim \limits_{n \to \infty} K_{n} = \alpha [/math] |
Beweis für die Irrationalität von [math] \sqrt{10} [/math]
Wir wissen, dass eine Zahl genau dann rational ist, wenn ihre Kettenbruchdarstellung endlich ist. Daher können wir zeigen, ob eine Zahl rational ist, indem wir ihre Kettenbruchdarstellung berechnen.
[math] \begin{align} \sqrt{10} &= 3 + (\sqrt{10} - 3) = 3 + \dfrac{(\sqrt{10} - 3)(\sqrt{10} + 3)}{3 + \sqrt{10}} = 3 + \dfrac{1}{3 + \sqrt{10}} \\ \\ &= 3 + \dfrac{1}{3+3+\dfrac{1} {3 + \sqrt{10}}} = 3 + \dfrac{1}{6+\dfrac{1} {3 + \sqrt{10}}} \\ \\ &= 3 + \dfrac{1}{6+\dfrac{1} {6 + \dfrac{1} {3 + \sqrt{10}}}} \\ \\ &= 3 + \dfrac{1}{6+\dfrac{1} {6 + \dfrac{1} {6 + \dfrac{1} {\hspace{10pt} \ddots}}}} \end{align} [/math]
Diese Darstellung bricht nie ab; [math] \sqrt{10} [/math] ist demnach irrational.
Berechnung des Wertes eines periodischen Kettenbruchs[5]
Sei [math] \xi [/math] eine reelle Zahl gegeben durch [math] \: \xi := 4 + \dfrac{1}{1+\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{2+\dfrac{1}{\hspace{10pt} \ddots}}}}}}} [/math]
Um einen ungefähren Wert von [math] \xi [/math] zu berechnen, reicht es, den Wert eines Partialbruchs des Kettenbruchs zu bestimmen:
[math] \: \xi \approx 4 + \dfrac{1}{1+\dfrac{1}{2+\dfrac{1}{3}}} = \dfrac{47}{10} [/math]
Da dieser Kettenbruch aber periodisch ist, können wir auch den exakten Wert von [math] \xi. [/math] berechnen. Dazu definieren wir
[math] \theta := 2+\dfrac{1}{3+\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{2+\dfrac{1}{\hspace{10pt} \ddots}}}}} [/math]
Es gilt [math] \: \theta = 2 + \dfrac{1}{3 + \dfrac{1}{\theta}} = 2 + \dfrac{\theta}{3\theta + 1} \\ \\
\Rightarrow \theta^{2} - 2\theta - \dfrac{2}{3} = 0 \\ \\
\Rightarrow \theta = \dfrac{3 + \sqrt{15}}{3} [/math]
[math] \Rightarrow \xi = 4 + \dfrac{1}{1+\dfrac{1}{\theta}} = 4 + \dfrac{\theta}{1 + \theta} = 4 + \dfrac{3 + \sqrt{15}}{6 + \sqrt{15}} = 4 + \dfrac{1 + \sqrt{15}}{7} = \dfrac{29 + \sqrt{15}}{7} [/math]
Wie in dieser Beispielrechnung zu sehen, ist der Wert eines jeden rein periodischen Kettenbruchs die irrationale Lösung eines quadratischen Polynoms mit rationalen Koeffizienten, eine so genannte quadratische Irrationalzahl. Tatsächlich lässt sich aber noch mehr zeigen.
Satz von Euler-Lagrange: Jeder periodische Kettenbruch ist eine quadratische Irrationalzahl und umgekehrt.
Kettenbruchdarstellung von [math] \pi [/math][6]
Da wir den ungefähren Wert von [math] \pi [/math] kennen, können wir es als regulären Kettenbruch entwickeln. Sei dazu [math] \left\lt a_0; a_1, a_2, \dots \right\gt := \pi [/math]
Es gilt
[math] 3\lt \pi \lt 4 \Rightarrow a_0 = 3 \\ \pi=3+(\pi-3) \; \; \; \; \dfrac{1}{8} \lt \pi-3 \lt \dfrac{1}{7} \Rightarrow a_1 = 7 \\ \pi=3+\dfrac{1}{7+(\dfrac{1}{\pi-3}-7)} \; \; \; \; \dfrac{1}{16} \lt \dfrac{1}{\pi-3}-7 \lt \dfrac{1}{15} \Rightarrow a_2 = 15 \\ \dots \\ [/math]
[math] \pi[/math][math] = 3+\dfrac{1}{7+\dfrac{1}{15+\dfrac{1}{1+\dfrac{1}{292+\dfrac{1}{1+{\dfrac{1}{\hspace{10pt} \ddots}}}}}}} [/math]
Werten wir die Partialbrüche dieses Kettenbruchs aus, sehen wir, dass sie eine gute Annäherung an [math] \pi [/math] liefern.
| [math] \begin{align} \pi &= 3.1415926535897932384626433832795028... \\ &= \left\lt 3;7,15,1,292,1,1,1,2,1,3,1,14,2,1,1,...\right\gt \end{align} [/math] | ||
|---|---|---|
| Partialbruch | ermittelter Bruch | Wert als Dezimalzahl |
| [math] \left\lt 3\right\gt [/math] | [math] \dfrac{3}{1} [/math] | 3.00000000000000... |
| [math]\left\lt 3;7\right\gt [/math] | [math]\dfrac{22}{7} [/math] | 3.14285714285714... |
| [math]\left\lt 3;7,15\right\gt [/math] | [math]\dfrac{333}{106} [/math] | 3.14150943396226... |
| [math]\left\lt 3;7,15,1\right\gt [/math] | [math]\dfrac{355}{113} [/math] | 3.14159292035398... |
| [math]\left\lt 3;7,15,1,292\right\gt [/math] | [math]\dfrac{103993}{33102} [/math] | 3.14159265301190... |
| [math]\left\lt 3;7,15,1,292,1\right\gt [/math] | [math]\dfrac{104348}{33215}[/math] | 3.14159265392142... |
| [math]\left\lt 3;7,15,1,292,1,1\right\gt [/math] | [math]\dfrac{208341}{66317} [/math] | 3.14159265346744... |
| [math]\left\lt 3;7,15,1,292,1,1,1\right\gt [/math] | [math]\dfrac{312689}{99532} [/math] | 3.14159265361894... |
| [math]\left\lt 3;7,15,1,292,1,1,1,2\right\gt [/math] | [math]\dfrac{833719}{265381} [/math] | 3.14159265358108... |
Da [math] \pi [/math] irrational ist und bisher keine Muster in dessen regulärem Kettenbruch gefunden wurden, können wir nur endliche Partialbrüche von diesem berechnen. Wenn wir uns aber nicht auf reguläre Kettenbrüche beschränken, gibt es Kettenbrüche von [math] \pi [/math], die Muster enthalten.[7]
So zeigte Johann Heinrich Lambert:
[math] \dfrac{4}{\pi}=1+\dfrac{1^2}{3+\dfrac{2^2}{5+\dfrac{3^2}{7+\dfrac{4^2}{9+\dfrac{5^2}{11+\dfrac{6^2}{\hspace{10pt} \ddots}}}}}} [/math]
Von Leonhard Euler stammt die Entwicklung:
[math] \pi= 1+\dfrac{1^2}{6+\dfrac{3^2}{6+\dfrac{5^2}{6+\dfrac{7^2}{6+\dfrac{9^2}{6+\dfrac{11^2}{\hspace{10pt} \ddots}}}}}} [/math]
Siehe auch
Einzelnachweise
- ↑ 1,0 1,1 Johannes Klee: Endliche Kettenbrüche (2019), Masterseminar WiSe 19/20 an der TU Dortmund
- ↑ Bild zu 17/10 wurde selbst hergestellt
- ↑ Bild zu 16/10 wurde selbst hergestellt
- ↑ Algorithmen für regelmäßige Kettenbrüche Stefan Scheel, Bachelorarbeit an der Universität Kassel (2005)
- ↑ Thomas Boecker: Periodische Kettenbrüche Seminar zur Algebra und Zahlentheorie, WiSe 19/20 an der TU Dortmund
- ↑ Continued Fraction Approximations to [math] \pi [/math] University of Illinois - Department of Mathematics
- ↑ Zur Arithmetik von Kettenbrüchen Philipp Stopp, Bachelorarbeit vorgelegt der Mathematisch-Naturwissenschaftlichen Fakultät der Universität des Saarlandes (2009)
Autoren
- Victoria Mezger
- Pirmin Kupffer
- Marvin Hertweck
- Paul Bruckert