Goldener Schnitt: Unterschied zwischen den Versionen
| Zeile 27: | Zeile 27: | ||
Natürlich gibt es keine irrationale Zahl die "irrationaler" als eine andere irrationale Zahl ist. <math>\Phi</math> lässt sich, wie wir im folgenden sehen werden nur sehr "langsam" durch rationale Zahlen annähern, daher die meist scherzhafte Aussage <math>\Phi</math> sei die "irrationalste" Zahl. | Natürlich gibt es keine irrationale Zahl die "irrationaler" als eine andere irrationale Zahl ist. <math>\Phi</math> lässt sich, wie wir im folgenden sehen werden nur sehr "langsam" durch rationale Zahlen annähern, daher die meist scherzhafte Aussage <math>\Phi</math> sei die "irrationalste" Zahl. | ||
| − | === Kettenbruchdarstellung === | + | === Kettenbruchdarstellung ([https://de.wikipedia.org/wiki/Kettenbruch mehr])=== |
Um die Annäherung durch rationale Zahlen vorzunehmen, stellt man die Zahl als unendlichen Kettenbruch dar und bricht diesen an einer Stelle ab. Je später, desto genauer die Annäherung. | Um die Annäherung durch rationale Zahlen vorzunehmen, stellt man die Zahl als unendlichen Kettenbruch dar und bricht diesen an einer Stelle ab. Je später, desto genauer die Annäherung. | ||
| − | + | ::<math> \Phi = 1 + \frac{1}{\Phi} = 1 + \frac{1}{1 + \frac{1}{\Phi}} = 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{\Phi}}} = 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{\Phi}}}} \quad ... </math> | |
| + | |||
| + | Wir sehen nun, dass der Kettenbruch von <math>\Phi</math> nur Einsen als Elemente enthält, woraus sich wiederum folgern lässt, dass der Nenner der Näherung durch rationale Zahlen so langsam wie nur möglich wächst und sich somit eine möglichst genaue Approximation nur schlecht durchzuführen lässt. | ||
| + | |||
| + | Daher, wie bereits erwähnt, die Aussage <math>\Phi</math> sei die irrationalste nur mögliche Zahl. | ||
| − | + | Sehr interessant ist hierbei, dass der Näherungsbruch immer aus zwei aufeinanderfolgenden [[Fibonacci-Zahlen]] besteht! | |
| − | {| class="wikitable mw-collapsible" | + | {| class="wikitable mw-collapsible centered" |
| − | |+ | + | |+Annäherung durch Kettenbruchverfahren |
| − | !Abbruch nach n Elementen | + | ! "style="width:7em;" |Abbruch nach n Elementen |
| − | !1 | + | ! style="width:3em;" |1 |
| − | !2 | + | ! style="width:3em;" |2 |
| − | !3 | + | ! style="width:3em;" |3 |
| − | !4 | + | ! style="width:3em;" |4 |
| − | !5 | + | ! style="width:3em;" |5 |
| − | !6 | + | ! style="width:3em;" |6 |
| − | !7 | + | ! style="width:3em;" |7 |
| − | !8 | + | ! style="width:3em;" |8 |
| − | ! rowspan="3" | <math>\vdots</math> | + | ! rowspan="3" style="width:1em;" | <math>\vdots</math> |
| − | ! rowspan="3" |Die rekursive Bildungsformel lautet: <br /> | + | ! rowspan="3" |Die rekursive Bildungsformel lautet: <br /> |
| − | <math> \frac{p_{n}}{q_{n}} = \frac{p_{n-1} + q_{n-1}}{p_{n-1}} </math> <br /> <br /> | + | <big> <math> \frac{p_{n}}{q_{n}} = \frac{p_{n-1} + q_{n-1}}{p_{n-1}} </math> </big> <br /> <br /> |
| − | ''mit <math> p_{0},q_{0} = 1 </math>'' | + | ''<small> mit <math> p_{0},q_{0} = 1 </math> </small>'' |
|- | |- | ||
|Näherungswert | |Näherungswert | ||
| − | |2 | + | | style="text-align:center;" |2 |
| − | |<math> \frac{3}{2} </math> | + | | style="text-align:center;" |<math> \frac{3}{2} </math> |
| − | |<math> \frac{5}{3} </math> | + | | style="text-align:center;" |<math> \frac{5}{3} </math> |
| − | |<math> \frac{8}{5} </math> | + | | style="text-align:center;" |<math> \frac{8}{5} </math> |
| − | |<math> \frac{13}{8} </math> | + | | style="text-align:center;" |<math> \frac{13}{8} </math> |
| − | |<math> \frac{21}{13} </math> | + | | style="text-align:center;" |<math> \frac{21}{13} </math> |
| − | |<math> \frac{34}{21} </math> | + | | style="text-align:center;" |<math> \frac{34}{21} </math> |
| − | |<math> \frac{55}{34} </math> | + | | style="text-align:center;" |<math> \frac{55}{34} </math> |
|- | |- | ||
| − | |Abweichung in % | + | |Abweichung von <math> \Phi </math> in % |
| − | |23,6 | + | | style="text-align:center;" |23,6 |
| − | |7,3 | + | | style="text-align:center;" |7,3 |
| − | |3 | + | | style="text-align:center;" |3 |
| − | |1,1 | + | | style="text-align:center;" |1,1 |
| − | |0,43 | + | | style="text-align:center;" |0,43 |
| − | |0,16 | + | | style="text-align:center;" |0,16 |
| − | |0,062 | + | | style="text-align:center;" |0,062 |
| − | |0,024 | + | | style="text-align:center;" |0,024 |
|} | |} | ||
| − | |||
| − | |||
| − | |||
=== Kettenwurzeldarstellung === | === Kettenwurzeldarstellung === | ||
Version vom 12. März 2021, 11:31 Uhr
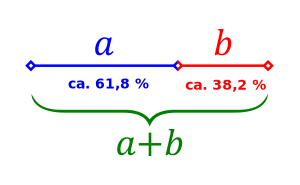
Der "Goldene Schnitt" bezeichnet allgemein ein spezielles Teilungsverhältnis einer Strecke.
Die Besonderheit dieses Verhältnisses besteht darin, die Gesamtstrecke in zwei Teile aufzuteilen, wobei die Gesamtstrecke dasselbe Teilungsverhältnis zur größeren Teilstrecke aufweist, wie auch die größere Teilstrecke zur kleineren Teilstrecke.
Den Quotient der Strecken nennt man die Goldene Zahl [math]\Phi[/math].
Herleitung des Goldenen Schnitts
Die Definition lässt sich algebraisch ausdrücken und wie folgt eindeutig lösen:
- [math] \Phi = \frac{a}{b} = \frac{a+b}{a} = 1+\frac{b}{a} = 1 + \frac{1}{\Phi}\\\\ [/math]
- [math] \Leftrightarrow \Phi^{2} = \Phi + 1 \\\\ [/math]
- [math] \Leftrightarrow 0 = \Phi^{2} - \Phi - 1 \\\\ [/math]
- [math] \Rightarrow \Phi_{1} = \frac{1+\sqrt[]{5}}{2} \approx 1,618\\ [/math]
- [math] \Rightarrow \Phi_{2} = \frac{1-\sqrt[]{5}}{2} \approx 0,618 = \frac{1}{\Phi_{1}} [/math]
Wir nennen [math] \Phi_{1} [/math] die Goldene Zahl [math] \Phi [/math] mit den Kehrwert [math] \frac{1}{\Phi}= \Phi - 1 [/math]
[math]\Phi[/math] als "irrationalste" Zahl
Natürlich gibt es keine irrationale Zahl die "irrationaler" als eine andere irrationale Zahl ist. [math]\Phi[/math] lässt sich, wie wir im folgenden sehen werden nur sehr "langsam" durch rationale Zahlen annähern, daher die meist scherzhafte Aussage [math]\Phi[/math] sei die "irrationalste" Zahl.
Kettenbruchdarstellung (mehr)
Um die Annäherung durch rationale Zahlen vorzunehmen, stellt man die Zahl als unendlichen Kettenbruch dar und bricht diesen an einer Stelle ab. Je später, desto genauer die Annäherung.
- [math] \Phi = 1 + \frac{1}{\Phi} = 1 + \frac{1}{1 + \frac{1}{\Phi}} = 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{\Phi}}} = 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{\Phi}}}} \quad ... [/math]
Wir sehen nun, dass der Kettenbruch von [math]\Phi[/math] nur Einsen als Elemente enthält, woraus sich wiederum folgern lässt, dass der Nenner der Näherung durch rationale Zahlen so langsam wie nur möglich wächst und sich somit eine möglichst genaue Approximation nur schlecht durchzuführen lässt.
Daher, wie bereits erwähnt, die Aussage [math]\Phi[/math] sei die irrationalste nur mögliche Zahl.
Sehr interessant ist hierbei, dass der Näherungsbruch immer aus zwei aufeinanderfolgenden Fibonacci-Zahlen besteht!
| Abbruch nach n Elementen | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | [math]\vdots[/math] | Die rekursive Bildungsformel lautet: [math] \frac{p_{n}}{q_{n}} = \frac{p_{n-1} + q_{n-1}}{p_{n-1}} [/math] |
|---|---|---|---|---|---|---|---|---|---|---|
| Näherungswert | 2 | [math] \frac{3}{2} [/math] | [math] \frac{5}{3} [/math] | [math] \frac{8}{5} [/math] | [math] \frac{13}{8} [/math] | [math] \frac{21}{13} [/math] | [math] \frac{34}{21} [/math] | [math] \frac{55}{34} [/math] | ||
| Abweichung von [math] \Phi [/math] in % | 23,6 | 7,3 | 3 | 1,1 | 0,43 | 0,16 | 0,062 | 0,024 |
Kettenwurzeldarstellung
Alternativ lässt sich [math]\Phi[/math] auch durch eine unendliche Kettenwurzel nähern, dies folgt aus [math]\Phi^{2} = \Phi + 1[/math]
- [math] \Phi = \sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+...}}}} [/math]
%Geometrische Konstruktion von [math]\Phi[/math]
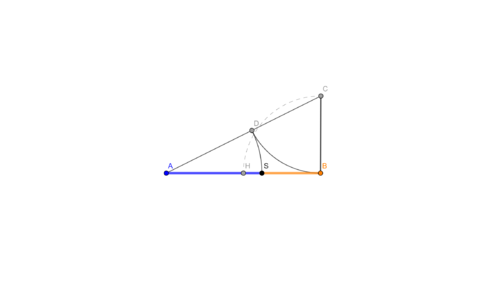
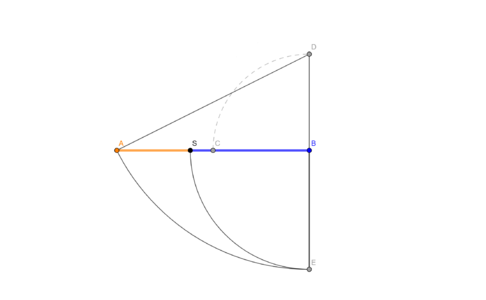
Unterscheidung in äußere und innere Teilung
| "klassische Methode" | |
| Euklid Methode |
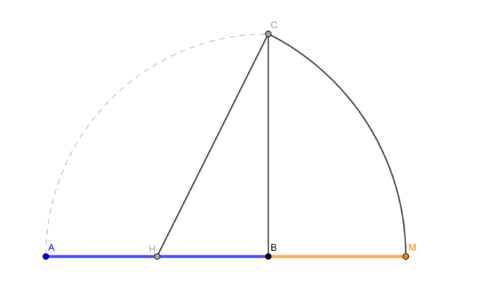
| "klassische Methode" | |
| George Odom |
Goldener Schnitt im Pentagramm
Goldenes Rechteck
Goldenes Dreieck(2 Möglichkeiten)
Goldener Winkel
%Goldener Schnitt in der Geschichte
Die erste genaue Beschreibung des Goldenen Schnitts stammt von Euklid %verlinkung?% (325-270 v.Chr.), jedoch ist umstritten ob die Entdeckung auf ihn oder auf einen früheren Mathematiker zurückzuführen ist. %(Hippasos von Metapont (spätes 6. Jahrhundert v. Chr.) oder auf Eudoxos von Knidos (um 370 v. Chr.))
An Popularität gewann er allerdings erst ab Mitte des 19. Jahrhunderts.
%Goldener Schnitt in Natur und Technik
Der Goldene Schnitt ist an vielen Stellen in der Natur zu beobachten, am einfachsten jedoch in der Pflanzenwelt. Viele Pflanzen stellen ihre Blätter im Goldenen Winkel zueinander auf, aus einem praktischen Grund: Durch diesen speziellen Winkel überlappen sich so wenig Blätter wie möglich, sodass die Pflanze die maximale Sonnenenergie aufnehmen kann.
Blütenstand der Sonnenblume
Bei der Sonnenblume lässt sich beobachten, dass die Blüten in der Form von rechts- und linksdrehenden Spiralen angeordnet sind. Das Interessante hieran ist, dass die Anzahl der jeweiligen Spiralen immer zwei aufeinander folgenden Fibonacci-Zahlen entspricht und der Winkelversatz der Spiralen immer dem Goldenen Winkel φ bzw. einer Ableitung dessen.
%Bahnresonanzen
%Schwarze Löcher
%Kristallstrukturen
Goldener Schnitt in Architektur
Leipziger Rathaus
Kölner Dom
Parthenon
Petersbasilika
Technik
Der Goldene Schnitt taucht unter anderem beim Geigenbau %(https://www.michael-holzapfel.de/themen/goldenerschnitt/gs-geige/geige.htm) und beim Bau von Ultraleichtflugzeugen %(https://www.imw.tu-clausthal.de/fileadmin/IMW/documents/Institutsmitteilungen/1998/98_31.pdf Seite 3/4) auf.