Die Feigenbaum Konstante: Unterschied zwischen den Versionen
Cv234 (Diskussion | Beiträge) |
(Logistische Funktion mit Beispielen) |
||
| Zeile 7: | Zeile 7: | ||
== Die Feigenbaum-Konstante == | == Die Feigenbaum-Konstante == | ||
[[Datei:LogisticMap BifurcationDiagram.png|alternativtext=Feigenbaum-Diagramm|mini|Das Feigenbaum-Diagramm]] | [[Datei:LogisticMap BifurcationDiagram.png|alternativtext=Feigenbaum-Diagramm|mini|Das Feigenbaum-Diagramm]] | ||
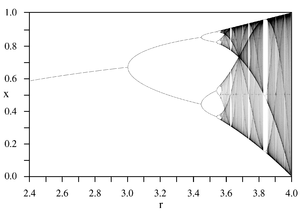
| − | Die Feigenbaum-Konstante spielt in der Chaosforschung eine ähnlich große Rolle wie π in der Geometrie. Sie bezeichnet das Verhältnis der Längen zwei aufeinander folgenden Intervallen, die durch "Gabeldungen" begrenzt sind. (Siehe Graphik "Feigenbaum-Diagramm") | + | Die Feigenbaum-Konstante spielt in der Chaosforschung eine ähnlich große Rolle wie π in der Geometrie. Sie bezeichnet den Wert gegen den das Verhältnis der Längen zwei aufeinander folgenden Intervallen, die durch "Gabeldungen" begrenzt sind, konvergiert. (Siehe Graphik "Feigenbaum-Diagramm") |
Die Zahl wurde von [https://de.wikipedia.org/wiki/Mitchell_Feigenbaum Mitchell Feigenbaum] im Jahr 1975 entdeckt und ihr Zahlenwert δ wurde 1977 von den Physikern Siegfried Großmann und Stefan Thomae erstmals bestimmt. | Die Zahl wurde von [https://de.wikipedia.org/wiki/Mitchell_Feigenbaum Mitchell Feigenbaum] im Jahr 1975 entdeckt und ihr Zahlenwert δ wurde 1977 von den Physikern Siegfried Großmann und Stefan Thomae erstmals bestimmt. | ||
| Zeile 14: | Zeile 14: | ||
== Die logistische Gleichung == | == Die logistische Gleichung == | ||
| − | Die logistische Gleichung wurde 1837 von [https://de.wikipedia.org/wiki/Pierre_Fran%C3%A7ois_Verhulst Pierre François Verhulst] eingeführt, um Populationen bzw deren Entwicklung modellhaft darzustellen. | + | Die logistische Gleichung wurde 1837 von [https://de.wikipedia.org/wiki/Pierre_Fran%C3%A7ois_Verhulst Pierre François Verhulst] eingeführt, um Populationen bzw. deren Entwicklung modellhaft darzustellen. Die Relevanz für die Feigenbaum-Konstante besteht darin, dass man den Wert an einer Stelle ''r'' im Feigenbaum-Diagramm auch als Grenzwert der Population mit dem entsprechenden Wachstumsfaktor interpretieren kann. |
Sei '''''X'''<sub>n</sub>'' die relative Größe einer Polulation zu einem Zeitpunkt ''n'' (zum Beispiel der Anteil der mit COVID-19 infizierten Menschen.) Man kann n als beliebiges Zeitntervall auffassen, so kann n beispielsweise Monate oder Jahre symbolisieren. '''''X'''<sub>0</sub>'' bezeichnet die Startpolulation zum Zeitpunkt ''n''=0. | Sei '''''X'''<sub>n</sub>'' die relative Größe einer Polulation zu einem Zeitpunkt ''n'' (zum Beispiel der Anteil der mit COVID-19 infizierten Menschen.) Man kann n als beliebiges Zeitntervall auffassen, so kann n beispielsweise Monate oder Jahre symbolisieren. '''''X'''<sub>0</sub>'' bezeichnet die Startpolulation zum Zeitpunkt ''n''=0. | ||
| Zeile 33: | Zeile 33: | ||
Das Verhalten der Funktion hängt vom Wachstumsfaktor ''r'' ab. | Das Verhalten der Funktion hängt vom Wachstumsfaktor ''r'' ab. | ||
| + | |||
| + | === Beispiele: === | ||
| + | Sei X0 = 0,5 (also die Hälfte der maximal möglichen Population) und r = 2,5. | ||
| + | |||
| + | Dann berechnet sich X1 = 2,5*0,5*(1-0,5) = 0,626, X2 ≈ 0,5859 , X3 ≈ 0,6065, X4 ≈ 0,5966, X5 ≈0,6017, usw. Die Folge der Xn nähert sich also dem Grenzwert 0,6 alternierend, wie man auch gut in der Graphik sehen kann. | ||
| + | |||
| + | Durch das selbe Beispiel mit Startwert X0 = 0,1 sieht man, dass der Grenzwert unabhängig von der Startpolulation ist.<gallery> | ||
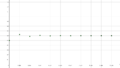
| + | Datei:Population mit r=2,5.png|alt=Entwicklung einer Startpolulation X0=0,5 über 10 Jahre mit einem Wachstumsfaktor r=2,5|Entwicklung einer Startpolulation X0=0,5 über 10 Jahre mit einem Wachstumsfaktor r=2,5 | ||
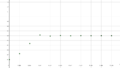
| + | Datei:R=2,5, x0 = 0,1.png|alt=Entwicklung einer Startpolulation X0=0,1 über 10 Jahre mit einem Wachstumsfaktor r=2,5|Entwicklung einer Startpolulation X0=0,1 über 10 Jahre mit einem Wachstumsfaktor r=2,5 | ||
| + | </gallery> | ||
| + | |||
| + | Folge deren Grenzwert in Abhängigkeit von r untersucht wird. | ||
_________________________________________________________________________________________________________________________________ | _________________________________________________________________________________________________________________________________ | ||
| Zeile 38: | Zeile 50: | ||
%(Hier kann ich (Christian) gerne noch weiterarbeiten, zb das stabilisierende Verhalten bei niedrigem r und das oszillierende Verhalten bei größrem r) | %(Hier kann ich (Christian) gerne noch weiterarbeiten, zb das stabilisierende Verhalten bei niedrigem r und das oszillierende Verhalten bei größrem r) | ||
| − | %%Das würde ich eher in Part 2 machen, da sich dort die verschiedenen r/lambda Werte angeschaut werden (aaron) | + | %%Das würde ich eher in Part 2 machen, da sich dort die verschiedenen r/lambda Werte angeschaut werden (aaron) jap, hast recht. |
%PART 1 .BASICS der Funktion (logistische Gleichung) https://de.wikipedia.org/wiki/Logistische_Gleichung | %PART 1 .BASICS der Funktion (logistische Gleichung) https://de.wikipedia.org/wiki/Logistische_Gleichung | ||
Version vom 30. März 2021, 09:13 Uhr
δ%% ich glaube wir sollten das Thema noch umbenennen in "Logistische Gleichungen und die Feigenbaumkonstante" da das hier 80%logistische gleichung ist, die man braucht für die herleitung der feigenbaumkonstante und für den bezug zum mandelbrotset
%-> find ich gut, aber ich weiß nicht wie man den Titel ändert.. Vlt müssen wir eine neue Seite erstellen.
%% HIER FRAGEN REINSCHREIBEN
Die Feigenbaum-Konstante
Die Feigenbaum-Konstante spielt in der Chaosforschung eine ähnlich große Rolle wie π in der Geometrie. Sie bezeichnet den Wert gegen den das Verhältnis der Längen zwei aufeinander folgenden Intervallen, die durch "Gabeldungen" begrenzt sind, konvergiert. (Siehe Graphik "Feigenbaum-Diagramm")
Die Zahl wurde von Mitchell Feigenbaum im Jahr 1975 entdeckt und ihr Zahlenwert δ wurde 1977 von den Physikern Siegfried Großmann und Stefan Thomae erstmals bestimmt.
Es gilt: δ ≈ 4,6692
Die logistische Gleichung
Die logistische Gleichung wurde 1837 von Pierre François Verhulst eingeführt, um Populationen bzw. deren Entwicklung modellhaft darzustellen. Die Relevanz für die Feigenbaum-Konstante besteht darin, dass man den Wert an einer Stelle r im Feigenbaum-Diagramm auch als Grenzwert der Population mit dem entsprechenden Wachstumsfaktor interpretieren kann.
Sei Xn die relative Größe einer Polulation zu einem Zeitpunkt n (zum Beispiel der Anteil der mit COVID-19 infizierten Menschen.) Man kann n als beliebiges Zeitntervall auffassen, so kann n beispielsweise Monate oder Jahre symbolisieren. X0 bezeichnet die Startpolulation zum Zeitpunkt n=0.
Dann berechnet sich die Population Xn+1 rekursiv mit der logistischen Gleichung:
%(TEXen?)
Xn+1 = r * Xn * (1 - Xn)
wobei der Parameter r der Wachstumsfaktor ist.
Die Gleichung berücksichtigt 2 Effekte:
1). Je größer die Population zum Zeitpunkt n ist, desto größer ist durch Vermehrung die nachfolgende Population.
2) Je näher die relative Größe der Population am Maximum (=1) ist, desto weniger Ressourcen (uninfizierte Menschen/Nahrung, ..) gibt es, sodass sich die Population wieder verringert.
Das Verhalten der Funktion hängt vom Wachstumsfaktor r ab.
Beispiele:
Sei X0 = 0,5 (also die Hälfte der maximal möglichen Population) und r = 2,5.
Dann berechnet sich X1 = 2,5*0,5*(1-0,5) = 0,626, X2 ≈ 0,5859 , X3 ≈ 0,6065, X4 ≈ 0,5966, X5 ≈0,6017, usw. Die Folge der Xn nähert sich also dem Grenzwert 0,6 alternierend, wie man auch gut in der Graphik sehen kann.
Durch das selbe Beispiel mit Startwert X0 = 0,1 sieht man, dass der Grenzwert unabhängig von der Startpolulation ist.
Folge deren Grenzwert in Abhängigkeit von r untersucht wird.
_________________________________________________________________________________________________________________________________
%(Hier kann ich (Christian) gerne noch weiterarbeiten, zb das stabilisierende Verhalten bei niedrigem r und das oszillierende Verhalten bei größrem r)
%%Das würde ich eher in Part 2 machen, da sich dort die verschiedenen r/lambda Werte angeschaut werden (aaron) jap, hast recht.
%PART 1 .BASICS der Funktion (logistische Gleichung) https://de.wikipedia.org/wiki/Logistische_Gleichung
%% beispiele anhand von Hasenpopulationen machen, Bilder mit kleinen niedlichen hasen einfügen, einer soll eine schrotflinte in der hand haben, und irgendwie den teil signalisieren , dass mehr hasen sterben als geboren werden wenn X_n nahe an 1 ist. die Folge X_n könnte dann z.b. die hasenpopulation darstellen in aufeinanderfolgenden Jahren
%% ==> mit X_n haben wir eine Folge (Ana1), X_0 muss dabei zwischen [0,1] sein (populationsstart sollte trivialerweise positiv sein und unter der oberen Schranke der Populationsgröße sein)
%% G>0
%% lambda>0 und kleiner als ____
%% beispiel für lambda (fest gewählt) benutzen und zeigen dass für verschiedene Startwerte die Konvergenz für n gegen unendlich sich nicht verändert und gegen den gleichen fixpunkt konvergiert, hier kann man zwei verschiedene X_0 benutzen und mit einer beispielrechnung zeigen, dass sie nach 10/20 schritten fast die gleichen ergebnisse haben
%%noch mehr Bilder mit süßen niedlichen hasen zeichnen
%PART 2: Der chaotische Graph https://upload.wikimedia.org/wikipedia/commons/7/7d/LogisticMap_BifurcationDiagram.png
%Wir bersprechen hier einen Graphen , dessen X Achse der lambda wert ist, und dessen y achse die häufungspunkte der Folge X_n mit diesem Lambda .
%(hier soll von links nach rechts der Graph immer ein bisschen mehr enthüllt werden)
%1.Teil : Tod ( 0=<lambda<= 1)
%DIe hasen population stirbt in jedem Fall aus, d.h. Die Fixpunkte sind null und somit auch Y-Wert
%Bild von Hasenfriedhof einzeichnen,soll aber trotzdem cute sein
%2.Teil : 1 Fixpunkt ( 1=<lambda<= 3)
%hier nähert sich die Population einem Fixpunkt an, man merkt auch dass es streng monoton wachsend ist
%3.Teil : 2 Fixpunkte(3<= lambda <= 1+Wurzel(6)) (ca.3.45))
%Die reihe konvergiert nicht mehr sondern hüpft zwischen zwei fixpunkten hin und her, der größere fixpunkt steigt monoton bei steigendem lambda, der kleiner fällt monoton
%4.Teil 2^n Fixpunkte (1+Wurzel(6)) (ca.3.45)<= lambda <= ca.3,57)
%die anzahl der fixpunkte verdoppeln sich immer häufiger.
%5.Teil Chaos (3.57 <=lambda <= 4)
%joa chaos halt, hier ist auch plötzliche die Änderung des Startwertes doch wieder von Interesse, da durch minimale Änderungen der Startwerte sich alles ändern kann. Es gibt jedoch ab und zu mal werte, welche sich wieder stabilisieren, sieht man gut im Graphen
%#Bild von hasen zeichnen , der aus der Wirklichkeit rausglitcht
%6.Teil Divergenz lambda >4
%hier divergiert die folge ins unendliche
% Part3: DIE KONSTANTE: hierzu betrachten wir den 3 und 4. Teil des Graphen. Def. Bifurkationsintervall: Intervall von lambda welche die gleiche anzahl häufungspunkte haben. zb. [3,3.45] hat zwei Häufuingspunkte, dies nennen wir jetzt mal A_1 und jedes drauffolgende A_n ist das zugehörige Intervall der Strecke mit 2^n Häufungspunkten.
%Teilen wir die Länge zweier beliebiger benachbarter A_n dann kommt die Feigenbaumkonstante raus.
%hier Bild einfügen der das Graphisch zeigt, am besten noch an zwei Stellen
%FBK = A_n/A_n+1
%Beispiel lässt sich hier gut durchrechnen mit A_2 und A_1
%nun lässt sich auch ausrechnen wann das Chaos beginnt, da wir mit A_n eine folge haben, welche immer kleiner wird (nullfolge) aka irgendwann die Verdopplung immer öfter passieren bis es dann zum chaos wird
% es lassen sich auch andere funktionen benutzen, dort wird die Feigenbaumkonstante auch wieder vorkommen als Verhältnis der Bifurkationsintervalle (hier müssen wir noch herausfinden, bei welchen Funktionen das zutrifft, im video ist als anderes Beispiel x_n+1= lambda*sin(x_N)
% PaRT4:bezug zum mandelbrotset,
%wenn man an bestimmten stellen ranzoomt, sieht der graph aus wie ein Fraktal
%hier wird definitiv ein querverweis auf das mandelbrotthema gemacht der anderen gruppe
%wenn man reelle zahlen einsetzt in die "mandelbrotfunktion" dann haben diese die gleiche anzahl an häufungspunkten wie die logistische funktion
% im veritasium video min 7 wird das gezeigt, hier gibts definitiv coole möglichkeiten gifs einzufügen,
% Part 5: andere bezüge (veritasium vid. min 11)
%AND THATS MY TED TALK, I WANNA THANK MA MUM GOODBYE