Cantor-Menge: Unterschied zwischen den Versionen
Zur Navigation springen
Zur Suche springen
| Zeile 2: | Zeile 2: | ||
= Geometrische Darstellung = | = Geometrische Darstellung = | ||
| + | |||
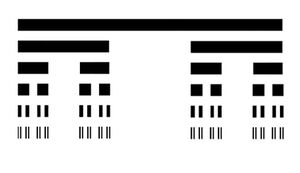
| + | Man konstruiert die Cantormenge rekursiv, indem man vom Intervall [0, 1] das mittlere offene Drittel (1/3, 2/3) entfernt, aus den beiden verbleibenden Intervallen [0, 1/3] und [2/3, 1] jeweils deren mittleren offenen Drittel entfernt und diesen Prozess unendlich fortsetzt. | ||
| + | |||
| + | Folgendes Bild veranschaulicht den Prozess: | ||
| + | [[Datei:Geometrische Veranschaulichung-.jpg|mini]] | ||
| + | |||
| + | |||
| + | Genauer gilt: | ||
| + | Bild nur bis eine Latex-formulierung von "Setze … >= 1" | ||
| + | Setze C := [0, 1] \ U n=1 ∞ Un ⊂ [0, 1] mit U1 := (1/3, 2/3) und Un+1 := {x/3 , (x + 2)/3 : x ∈ Un}, n ≥ 1. | ||
= Cantorfunktion = | = Cantorfunktion = | ||
Version vom 29. März 2021, 17:09 Uhr
Der Weg zur Cantormenge/Georg Cantor
Geometrische Darstellung
Man konstruiert die Cantormenge rekursiv, indem man vom Intervall [0, 1] das mittlere offene Drittel (1/3, 2/3) entfernt, aus den beiden verbleibenden Intervallen [0, 1/3] und [2/3, 1] jeweils deren mittleren offenen Drittel entfernt und diesen Prozess unendlich fortsetzt.
Folgendes Bild veranschaulicht den Prozess:
Genauer gilt:
Bild nur bis eine Latex-formulierung von "Setze … >= 1"
Setze C := [0, 1] \ U n=1 ∞ Un ⊂ [0, 1] mit U1 := (1/3, 2/3) und Un+1 := {x/3 , (x + 2)/3 : x ∈ Un}, n ≥ 1.