Cantor-Menge: Unterschied zwischen den Versionen
| Zeile 12: | Zeile 12: | ||
Genauer gilt: | Genauer gilt: | ||
| − | Setze C := [0, 1] \ \bigcup_{\lambda\in\Lambda} A_\lambda ⊂ [0, 1] mit U1 := (1/3, 2/3) und Un+1 := {x/3 , (x + 2)/3 : x ∈ Un}, n ≥ 1. | + | Setze C := [0, 1] \ \bigcup_{\lambda\in\Lambda} A_\lambda |
| + | |||
| + | ⊂ [0, 1] mit U1 := (1/3, 2/3) und Un+1 := {x/3 , (x + 2)/3 : x ∈ Un}, n ≥ 1. | ||
= Cantorfunktion = | = Cantorfunktion = | ||
Version vom 29. März 2021, 17:46 Uhr
Der Weg zur Cantormenge/Georg Cantor
1884 veröffentlicht Cantor sein Werk Über unendliche, lineare Punktmannigfaltigkeiten (VI). Im Paragraph § 19 beschäftigt er sich mit perfekten Teilmengen von ℝ. Hierzu verwendet er die Cantormenge und zeigt, dass jede beschränkte nichtleere perfekte Teilmenge von ℝ, die keine nichttrivialen Intervalle enthält, ähnlich ist zur Cantormenge C.
Geometrische Darstellung
Man konstruiert die Cantormenge rekursiv, indem man vom Intervall [0, 1] das mittlere offene Drittel (1/3, 2/3) entfernt, aus den beiden verbleibenden Intervallen [0, 1/3] und [2/3, 1] jeweils deren mittleren offenen Drittel entfernt und diesen Prozess unendlich fortsetzt.
Folgendes Bild veranschaulicht den Prozess.
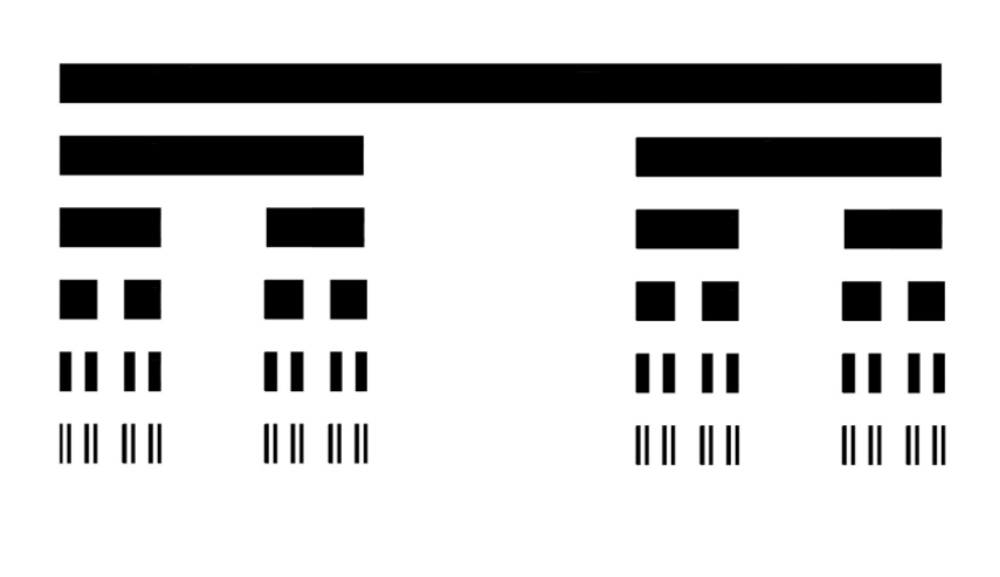
Genauer gilt: Setze C := [0, 1] \ \bigcup_{\lambda\in\Lambda} A_\lambda
⊂ [0, 1] mit U1 := (1/3, 2/3) und Un+1 := {x/3 , (x + 2)/3 : x ∈ Un}, n ≥ 1.
Cantorfunktion
Mit Hilfe der Cantormenge kann man rekursiv die sogenannte Cantorfunktion (auch “Teufelstreppe”) definieren. Sei f: [0,1] -> [0,1] mit f(0) = 0 und f(1) = 1. Sei x in [0,1], dann erhalte f(x) durch die folgenden Schritte:
- Drücke x in Basis 3 aus.
- Wenn x eine 1 enthält, ersetze jede Ziffer streng nach der ersten 1 durch 0.
- Ersetze alle verbleibenden 2s durch 1s.
- Interpretiere das Ergebnis als Binärzahl.
Der Graph der Funktion ist durch folgendes Bild veranschaulicht.
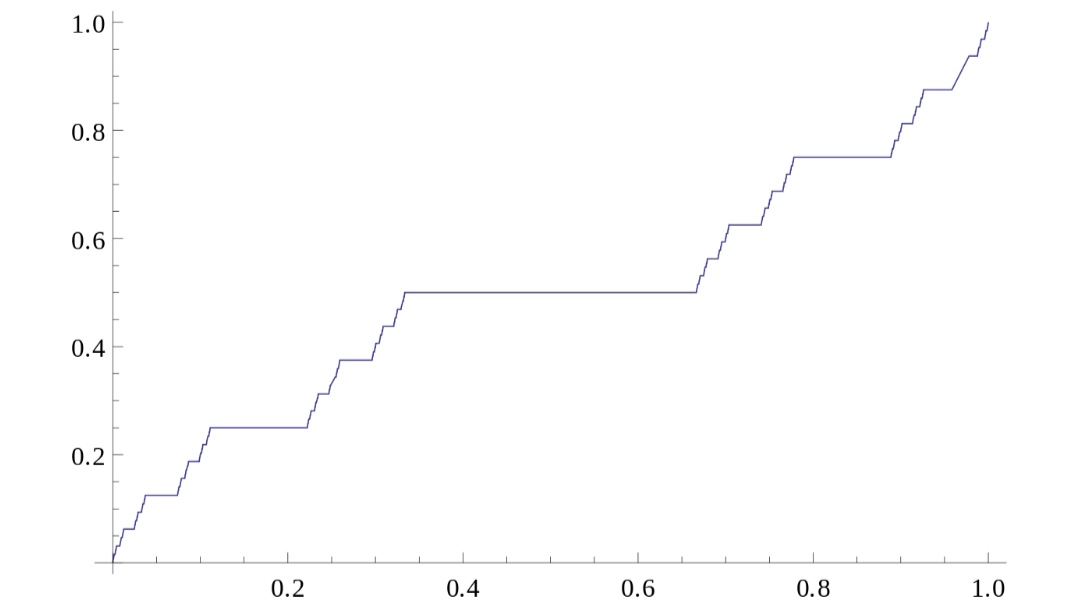
f ist monoton steigend und in allen Punkten x ∈ [0, 1] \ C differenzierbar mit Ableitung gleich 0. In 0, 1 und den Randpunkten der entfernten Drittelintervalle ist f nicht differenzierbar.
Sie steht in Bezug mit einer besonderen Wahrscheinlichkeitsverteilung.