Cantor-Menge: Unterschied zwischen den Versionen
| Zeile 12: | Zeile 12: | ||
Der internationale Standard sieht das Dezimalsystem als Zahlensystem vor. Dabei wird ein Zahlenwert dargestellt durch Ziffern 0,1,2,3,4,5,6,7,8,9 mit dem Stellenwert als Zehnerpotenz insgesamt addiert wird. Da bei der Cantor-Menge Intervalle iterativ gedrittelt werden, ist es ratsam sich für die nähere Betrachtung der Menge mit dem Stellenwertsystem zur Basis 3 vertraut zu machen, dem Tenär-System. Dieses sieht die Ziffern 0,1,2, und den Stellenwert als Dreierpotenz vor. Das heißt: | Der internationale Standard sieht das Dezimalsystem als Zahlensystem vor. Dabei wird ein Zahlenwert dargestellt durch Ziffern 0,1,2,3,4,5,6,7,8,9 mit dem Stellenwert als Zehnerpotenz insgesamt addiert wird. Da bei der Cantor-Menge Intervalle iterativ gedrittelt werden, ist es ratsam sich für die nähere Betrachtung der Menge mit dem Stellenwertsystem zur Basis 3 vertraut zu machen, dem Tenär-System. Dieses sieht die Ziffern 0,1,2, und den Stellenwert als Dreierpotenz vor. Das heißt: | ||
| − | + | Dezimalsystem: <br> | |
| + | x e [0, 1] x = 0,x<sub>1</sub>x<sub>2</sub>x<sub>3</sub>… = \sum .. x<sub>i</sub> 1/10<sup>i</sup> * x<sub>i</sub> e {0,1,...,9} | ||
| − | + | Tenärsystem: <br> | |
| + | x e [0, 1] x = 0,x<sub>1</sub>x<sub>2</sub>x<sub>3</sub>… = \sum .. x<sub>i</sub> 1/3<sup>i</sup> * x<sub>i</sub> e {0,1,2} | ||
Dazu x Beispiele | Dazu x Beispiele | ||
| Zeile 26: | Zeile 28: | ||
=> NEUEs BILD mit Brüchen? | => NEUEs BILD mit Brüchen? | ||
| − | So wie im Dezimalsystem die Konvention besteht 9 Periode mit 1 gleichzusetzten,gilt dies für Periode 2 im Tenärsystem. Also = 0,2 P = 1 0,02P =0,1 0,002P=0,01 … | + | So wie im Dezimalsystem die Konvention besteht 0,9 Periode mit 1 gleichzusetzten,gilt dies für Periode 2 im Tenärsystem. Also = 0,2 P = 1 0,02P =0,1 0,002P=0,01 … |
Angewand auf die Cantor-Menge bedeutet das, da das mittlere Intervall mit einer 1 als Stellenwert herausgenommen wird, dass die Menge Cn aus Elementen besteht, die innerhalb denr ersten n-Nachkommstellen nur aus den Ziffern 0 und 2 bestehen. Das erleichtert die Zuordnug | Angewand auf die Cantor-Menge bedeutet das, da das mittlere Intervall mit einer 1 als Stellenwert herausgenommen wird, dass die Menge Cn aus Elementen besteht, die innerhalb denr ersten n-Nachkommstellen nur aus den Ziffern 0 und 2 bestehen. Das erleichtert die Zuordnug | ||
Version vom 29. März 2021, 22:00 Uhr
Georg Cantor
Der 1845 in Sankt Petersburg geborene Georg Ferdinand Ludwig Philipp Cantor
Geometrische Darstellung
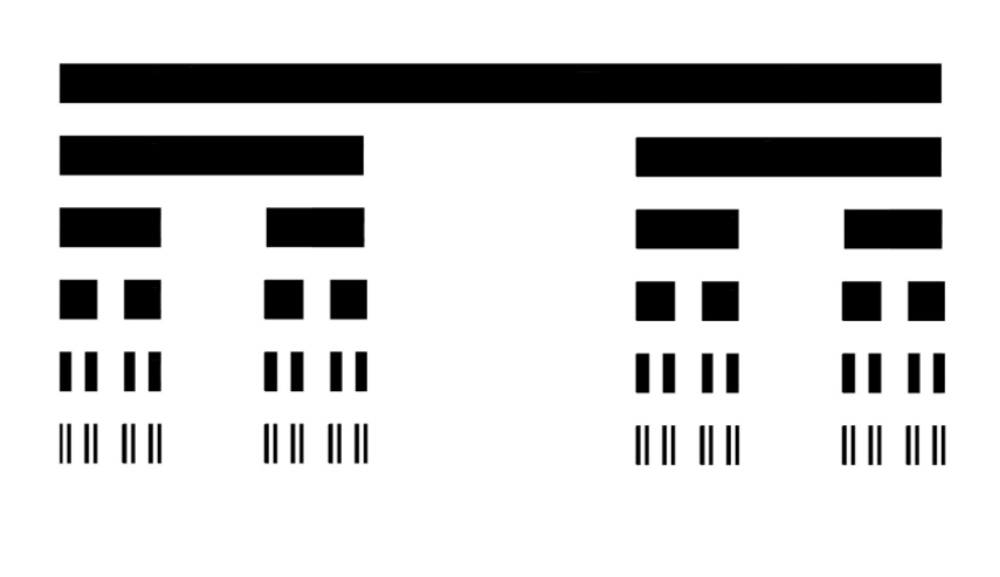
Man konstruiert die Cantor-Menge rekursiv, indem man vom abgeschlossenen Intervall [0, 1] das mittlere offene Drittel (1/3, 2/3) entfernt und aus den beiden verbleibenden Intervallen [0, 1/3] und [2/3, 1] erneut jeweils deren mittleres offenes Drittel entfernt. Dieser Prozess des Entfernen des mittleren offenen Drittels wird unendlich oft fortgesetzt.
Folgendes Bild veranschaulicht den Prozess.
Tenär-Dartstellung
Der internationale Standard sieht das Dezimalsystem als Zahlensystem vor. Dabei wird ein Zahlenwert dargestellt durch Ziffern 0,1,2,3,4,5,6,7,8,9 mit dem Stellenwert als Zehnerpotenz insgesamt addiert wird. Da bei der Cantor-Menge Intervalle iterativ gedrittelt werden, ist es ratsam sich für die nähere Betrachtung der Menge mit dem Stellenwertsystem zur Basis 3 vertraut zu machen, dem Tenär-System. Dieses sieht die Ziffern 0,1,2, und den Stellenwert als Dreierpotenz vor. Das heißt:
Dezimalsystem:
x e [0, 1] x = 0,x1x2x3… = \sum .. xi 1/10i * xi e {0,1,...,9}
Tenärsystem:
x e [0, 1] x = 0,x1x2x3… = \sum .. xi 1/3i * xi e {0,1,2}
Dazu x Beispiele
¼
⅓
1/9 11/27= …+
=> NEUEs BILD mit Brüchen?
So wie im Dezimalsystem die Konvention besteht 0,9 Periode mit 1 gleichzusetzten,gilt dies für Periode 2 im Tenärsystem. Also = 0,2 P = 1 0,02P =0,1 0,002P=0,01 …
Angewand auf die Cantor-Menge bedeutet das, da das mittlere Intervall mit einer 1 als Stellenwert herausgenommen wird, dass die Menge Cn aus Elementen besteht, die innerhalb denr ersten n-Nachkommstellen nur aus den Ziffern 0 und 2 bestehen. Das erleichtert die Zuordnug
Cantorfunktion
Mit Hilfe der Cantormenge lässt sich rekursiv die sogenannte Cantorfunktion (auch “Teufelstreppe”) definieren. Sei f: [0,1] -> [0,1] mit f(0) = 0 und f(1) = 1. Sei x in [0,1], dann erhalten wir die Cantorfunktion f(x) durch die folgenden Schritte:
- Drücke x in Basis 3 aus. ((Tenärsdarstellung?? Vielleicht sollten wir dann hier die Reihenfolge ändern?))
- Wenn x eine 1 enthält, ersetze jede Ziffer streng nach der ersten 1 durch 0.
- Ersetze alle verbleibenden 2en durch 1en.
- Interpretiere das Ergebnis als Binärzahl.
((-> Erschließt sich dadurch nicht auch die Gleichmächtigkeit zum Intervall [0, 1] ?? Dann könnte man hier den Beweis dazu noch einfügen ))
Der Graph der Funktion ist durch folgendes Bild veranschaulicht.
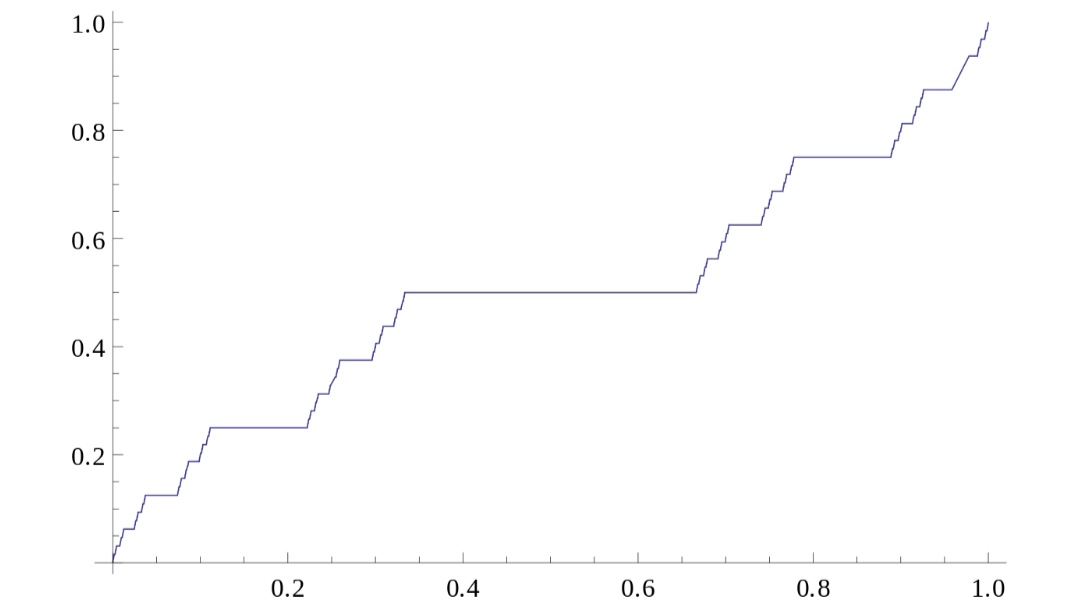
Die Teufelstreppe f ist monoton steigend und in allen Punkten x ∈ [0, 1] \ C differenzierbar mit der Ableitung 0, da sie dort konstant ist. In den Elementen der Cantormenge wie zum Beispiel 0 und 1 und den Randpunkten der entfernten Drittelintervalle ist f nicht differenzierbar. ((Beweis?? Bildnachweis?? Sollten wir hier nicht eine Achsenbeschriftung in Tenärdarstellung wählen oder zusätzlich angeben?))
Sie steht in Bezug mit einer besonderen Wahrscheinlichkeitsverteilung.
Eigenschaften
1884 veröffentlicht Cantor sein Werk Über unendliche, lineare Punktmannigfaltigkeiten (VI). Im Paragraph § 19 beschäftigt er sich mit perfekten Teilmengen von ℝ. Hierzu verwendet er die Cantormenge und zeigt, dass jede beschränkte nichtleere perfekte Teilmenge von ℝ, die keine nichttrivialen Intervalle enthält, ähnlich ist zur Cantormenge C.
In der Tat hat die Cantormenge besondere Eigenschaften:
Cantor und Ligeti (musikalische Interpretation?)
Der rumänische Komponist György Ligeti macht in seiner Komposition "L'escalier du diable" (“Die Teufelstreppe”) innerhalb seiner 13. Etüde die Cantor-Funktion musikalisch fühlbar.
Der endliche Aufstieg des Intervalls [0, 1] in überabzählbar unendlich vielen Schritten ist harmonisch selbstähnlich illustriert. Während meistens konstant, aufgrund der herausgenommen Intervall ist die Cantorfunktion, wie schon erwähnt, eigentlich monoton steigend. Deswegen beschleunigt das Tempo der Komposition.
Ihre Struktur ist dreiteilig. Nach dem ersten musikalischen Intervall wird das mittlere Teil des nächsten Intervall verändert und dann nochmals mit einem veränderten Mittlere geteilt.
Also versucht die Komposition eine Darstellung der Unendlichkeit zu geben, was in der Mathematik formal möglich ist.