Die Feigenbaum Konstante: Unterschied zwischen den Versionen
(Aufgeräumt) |
Cv234 (Diskussion | Beiträge) |
||
| Zeile 62: | Zeile 62: | ||
(#außerdem sollt ihr das Diagramm 1 bearbeiten, fügt farbige Boxen ein und schreibt die römischen zahlen rein, wie sie hier definiert sind von den Längen auf der XAchse) | (#außerdem sollt ihr das Diagramm 1 bearbeiten, fügt farbige Boxen ein und schreibt die römischen zahlen rein, wie sie hier definiert sind von den Längen auf der XAchse) | ||
| − | '''Fall''' <math>\boldsymbol{I}: 0 \le r \le 1</math><blockquote> | + | === '''Fall''' <math>\boldsymbol{I}: 0 \le r \le 1</math> === |
| + | <blockquote> | ||
Die Folge konvergiert gegen 0, d.h. die zu simulierende Populationen würden bei längerer Laufzeit aussterben. | Die Folge konvergiert gegen 0, d.h. die zu simulierende Populationen würden bei längerer Laufzeit aussterben. | ||
| − | </blockquote>'''Fall''' <math>\boldsymbol{II}: 1 < r \le 3</math><blockquote> | + | </blockquote> |
| + | |||
| + | === '''Fall''' <math>\boldsymbol{II}: 1 < r \le 3</math> === | ||
| + | <blockquote> | ||
Die Folge/Population konvergiert gegen den Grenzwert <math>\frac{(r-1)}{r}</math>. | Die Folge/Population konvergiert gegen den Grenzwert <math>\frac{(r-1)}{r}</math>. | ||
Je größer <math>r</math>ist, desto größer ist auch der Grenzwert, also die stabilisierte Größe der Population. | Je größer <math>r</math>ist, desto größer ist auch der Grenzwert, also die stabilisierte Größe der Population. | ||
| − | </blockquote>'''Fall''' <math>\boldsymbol{III}: 3 < r \le 1+\sqrt{6} \sim(3.45)</math><blockquote> | + | </blockquote> |
| + | |||
| + | === '''Fall''' <math>\boldsymbol{III}: 3 < r \le 1+\sqrt{6} \sim(3.45)</math> === | ||
| + | <blockquote> | ||
Die Folge/Population springt zwischen 2 Häufungspunkten. | Die Folge/Population springt zwischen 2 Häufungspunkten. | ||
</blockquote> | </blockquote> | ||
| − | === Beispiel === | + | ==== Beispiel ==== |
[[Datei:R=3,2.png|alternativtext=r = 3,2: Population mit 2 Häufungspunkten|mini|Graphik 4: r = 3.2, Folge mit 2 Häufungspunkten]] | [[Datei:R=3,2.png|alternativtext=r = 3,2: Population mit 2 Häufungspunkten|mini|Graphik 4: r = 3.2, Folge mit 2 Häufungspunkten]] | ||
<math>\boldsymbol{X}_0 = 0,5 </math> und <math>r = 3,2</math>. Die darauf basierende Folge hat die Häufungspunkte H<sub>1</sub>≈ 0,513 und H<sub>2</sub> ≈ 0.8 (siehe Graphik 4). | <math>\boldsymbol{X}_0 = 0,5 </math> und <math>r = 3,2</math>. Die darauf basierende Folge hat die Häufungspunkte H<sub>1</sub>≈ 0,513 und H<sub>2</sub> ≈ 0.8 (siehe Graphik 4). | ||
| Zeile 82: | Zeile 89: | ||
Der größere der beiden Häufungspunkte ist mit wachsendem <math>r</math> streng monoton steigend, der kleinere Häufungspunkt ist streng monoton fallend | Der größere der beiden Häufungspunkte ist mit wachsendem <math>r</math> streng monoton steigend, der kleinere Häufungspunkt ist streng monoton fallend | ||
| − | '''Fall''' <math>\boldsymbol{IV}: 1+\sqrt{6} \sim(3.45) \le r < 3,57 </math> | + | === '''Fall''' <math>\boldsymbol{IV}: 1+\sqrt{6} \sim(3.45) \le r < 3,57 </math> === |
| − | |||
Bei ca. 3.45 fängt die zweite Bifurkation an und es gibt nun 4 Häufungspunkte | Bei ca. 3.45 fängt die zweite Bifurkation an und es gibt nun 4 Häufungspunkte | ||
| Zeile 90: | Zeile 96: | ||
Das Verhältnis der Längen zwei aufeinander folgender Intervalle konvergiert genau gegen die Feigenbaumkonstante δ ≈ 4,6692. | Das Verhältnis der Längen zwei aufeinander folgender Intervalle konvergiert genau gegen die Feigenbaumkonstante δ ≈ 4,6692. | ||
| − | '''Fall''' <math>\boldsymbol{V}: 3,57 \le r < 4</math> | + | === '''Fall''' <math>\boldsymbol{V}: 3,57 \le r < 4</math> === |
| − | |||
nachdem sich die Anzahl der Häufungspunkte mit steigendem <math>r</math> bis zu 3.57 immer schneller verdoppelt fängt ab 3.57 plötzlich Chaos an. Die Folgen konvergieren nicht mehr gegen eine endlich Anzahl an Häufungspunkten, sondern bleiben chaotisch. Bei diesen chaotischen Parametern spielt auch der Anfangswert wieder eine Rolle, da er nun maßgeblich die Folge bestimmt. | nachdem sich die Anzahl der Häufungspunkte mit steigendem <math>r</math> bis zu 3.57 immer schneller verdoppelt fängt ab 3.57 plötzlich Chaos an. Die Folgen konvergieren nicht mehr gegen eine endlich Anzahl an Häufungspunkten, sondern bleiben chaotisch. Bei diesen chaotischen Parametern spielt auch der Anfangswert wieder eine Rolle, da er nun maßgeblich die Folge bestimmt. | ||
| Zeile 98: | Zeile 103: | ||
Schlussendlich liegen die nicht chaotischen Parameter dicht in diesem Bereich, d.h. in jedem noch so kleinen Teilintervall aus diesem Bereich befinden sich Parameter, mit denen die Folge gegen eine endliche Anzahl an Häufungspunkten konvergiert | Schlussendlich liegen die nicht chaotischen Parameter dicht in diesem Bereich, d.h. in jedem noch so kleinen Teilintervall aus diesem Bereich befinden sich Parameter, mit denen die Folge gegen eine endliche Anzahl an Häufungspunkten konvergiert | ||
| − | '''Fall''' <math>\boldsymbol{VI}: 4 ≤ r</math> | + | === '''Fall''' <math>\boldsymbol{VI}: 4 ≤ r</math> === |
| − | |||
Die Folge wächst monoton und überschreitet somit auch bei einem groß gewählten <math>n</math> irgendwann die obere Populationsgrenze, und ist damit für Bevölkerungssimulationen nicht zu gebrauchen. Schlussendlich divergiert sie gegen <math>+ \infty</math> | Die Folge wächst monoton und überschreitet somit auch bei einem groß gewählten <math>n</math> irgendwann die obere Populationsgrenze, und ist damit für Bevölkerungssimulationen nicht zu gebrauchen. Schlussendlich divergiert sie gegen <math>+ \infty</math> | ||
Version vom 31. März 2021, 12:08 Uhr
Die Feigenbaum-Konstante
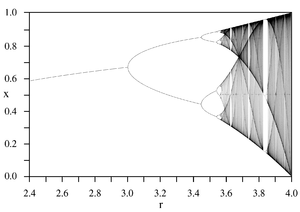
Die Feigenbaum-Konstante spielt in der Chaosforschung eine ähnlich große Rolle wie π in der Geometrie. Sie bezeichnet den Wert gegen den das Verhältnis der Längen zwei aufeinander folgender Intervalle, die durch "Gabeldungen" (Bifurkationen) begrenzt sind, konvergiert. (Siehe Graphik "Feigenbaum-Diagramm")
Die Zahl wurde von Mitchell Feigenbaum im Jahr 1975 entdeckt und ihr Zahlenwert [math]\delta[/math] wurde 1977 von den Physikern Siegfried Großmann und Stefan Thomae erstmals bestimmt.
Es gilt: [math]\delta\approx 4,6692[/math]
Die logistische Gleichung
Die logistische Gleichung wurde 1837 von Pierre François Verhulst eingeführt, um Populationen bzw. deren Entwicklung modellhaft darzustellen. Die Relevanz für die Feigenbaum-Konstante besteht darin, dass man den Wert an einer Stelle [math]r[/math] im Feigenbaum-Diagramm auch als Grenzwert der Population mit dem entsprechenden Wachstumsfaktor interpretieren kann.
Sei [math]\boldsymbol{X}_n[/math] die relative Größe einer Polulation zu einem Zeitpunkt [math]n[/math] (zum Beispiel der Anteil der mit COVID-19 infizierten Menschen.) Man kann [math]n[/math] als beliebiges Zeitntervall auffassen, so kann [math]n[/math] beispielsweise Monate oder Jahre symbolisieren. [math]\boldsymbol{X}_0[/math] bezeichnet die Startpolulation zum Zeitpunkt [math]n = 0[/math].
Dann berechnet sich die Population [math]\boldsymbol{X}_{n+1}[/math] rekursiv mit der logistischen Gleichung:
[math]\boldsymbol{X}_{n+1} = r*\boldsymbol{X}_n * (1-\boldsymbol{X}_n) [/math]
wobei der Parameter [math]r[/math] der Wachstumsfaktor ist.
Die Gleichung berücksichtigt 2 Effekte:
1). Je größer die Population zum Zeitpunkt [math]n[/math] ist, desto größer ist durch Vermehrung die nachfolgende Population.
2) Je näher die relative Größe der Population am Maximum (=1) ist, desto weniger Ressourcen (uninfizierte Menschen/Nahrung, ..) gibt es, sodass sich die Population wieder verringert.
Dadurch dass eine Population durch die vorherige berechnet wird, kann man [math](\boldsymbol{X}_{n})_{n\in\mathbb{N}}[/math] als rekursiv definierte Folge mit Startwert [math]\boldsymbol{X}_{0}[/math] auffassen. Dabei muss [math]\boldsymbol{X}_{0}\in\lbrack 0,1\rbrack[/math] gelten, denn trivialerweise muss die Population positiv sein und nicht größer als die obere Schranke.
Das Verhalten der Folge hängt vom Wachstumsfaktor [math]r[/math] ab. Dieser muss positiv sein (um negative Populationen zu vermeiden) und sollte kleiner als 4 sein, da die Folge sonst gegen [math]+\infty[/math] divergiert und sie den Zweck der Modellierung verfehlt.
Der Grentzwert der Folge
Der Grenzwert der Folge, wenn er existiert, ist unabhängig von dem Startwert [math]\boldsymbol{X}_0[/math] und wird nur durch [math]r[/math] bestimmt.
Das ist leicht daran erkennbar, dass für [math]n \rightarrow \infty[/math] gilt: [math]\boldsymbol{X}_{n+1} = \boldsymbol{X}_n[/math] und somit mit [math]\boldsymbol{g}:=\lim\limits_{n \to \infty}\boldsymbol{X}_n[/math]
[math]\boldsymbol{g} = r*\boldsymbol{g} * (1-\boldsymbol{g}) [/math]
[math]\Rightarrow 1=r-r*\boldsymbol{g}[/math]
[math]\Rightarrow r*\boldsymbol{g}=r-1[/math]
[math]\Rightarrow \boldsymbol{g}=\frac{(r-1)}{r}[/math]
Beispiele:
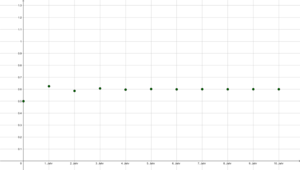
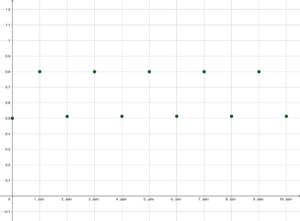
Sei [math]\boldsymbol{X}_0 = 0,5[/math] (also die Hälfte der maximal möglichen Population) und [math]r=2,5[/math].
Dann berechnet sich [math]\boldsymbol{X}_1 = 2,5*0,5*(1-0,5)=0,626 [/math], [math]\boldsymbol{X}_2 \approx 0,5859[/math], [math]\boldsymbol{X}_3 \approx 0,6065[/math], [math]\boldsymbol{X}_4 \approx 0,5966[/math], [math]\boldsymbol{X}_5 \approx 0,6017[/math], usw. Die Folge der [math]\boldsymbol{X}_n[/math] nähert sich also dem Grenzwert [math]\frac{(2,5-1)}{2,5} = 0,6[/math] alternierend, wie man auch gut in Graphik 1 sehen kann.
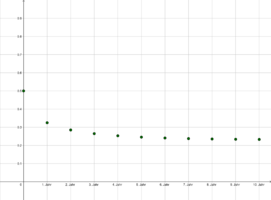
Durch das selbe Beispiel mit Startwert [math]\boldsymbol{X}_0 = 0,1[/math] sieht man, dass der Grenzwert unabhängig von der Startpopulation ist (Graphik 2).
Bei einem geringeren Wachstumsfaktor [math]r[/math] ist auch der Grenzwert kleiner (Graphik 3).
Verhalten in Abhängigkeit von r
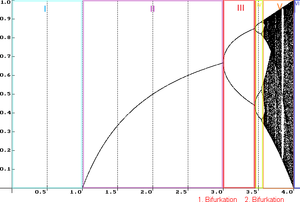
Wenn auf der x-Achse der Wert von [math]r[/math] aufgetragen wird und auf der y-Achse der entsprechende Grenzwert der Population, ergibt sich stückweise folgendes Diagramm 1:
(#außerdem sollt ihr das Diagramm 1 bearbeiten, fügt farbige Boxen ein und schreibt die römischen zahlen rein, wie sie hier definiert sind von den Längen auf der XAchse)
Fall [math]\boldsymbol{I}: 0 \le r \le 1[/math]
Die Folge konvergiert gegen 0, d.h. die zu simulierende Populationen würden bei längerer Laufzeit aussterben.
Fall [math]\boldsymbol{II}: 1 \lt r \le 3[/math]
Die Folge/Population konvergiert gegen den Grenzwert [math]\frac{(r-1)}{r}[/math].
Je größer [math]r[/math]ist, desto größer ist auch der Grenzwert, also die stabilisierte Größe der Population.
Fall [math]\boldsymbol{III}: 3 \lt r \le 1+\sqrt{6} \sim(3.45)[/math]
Die Folge/Population springt zwischen 2 Häufungspunkten.
Beispiel
[math]\boldsymbol{X}_0 = 0,5 [/math] und [math]r = 3,2[/math]. Die darauf basierende Folge hat die Häufungspunkte H1≈ 0,513 und H2 ≈ 0.8 (siehe Graphik 4).
Intuitiv kann man sich das so vorstellen, dass eine Population die zu schnell wächst, bereits im 1. Jahr eine Größe erreicht, sodass nicht mehr genügend Ressourcen vorhanden sind. Infolgedessen schrumpft die Population im Folgejahr wieder. Durch ihr starkes Wachstum hat sie im 3. Jahr aber bereits wieder die Überbevölkerung. Auf diese Weise ist jene Population stets am oszilieren.
Das führt zu der Bifurkation (Gabelung) im Diagramm 1 bei [math]r = 3[/math].
Der größere der beiden Häufungspunkte ist mit wachsendem [math]r[/math] streng monoton steigend, der kleinere Häufungspunkt ist streng monoton fallend
Fall [math]\boldsymbol{IV}: 1+\sqrt{6} \sim(3.45) \le r \lt 3,57 [/math]
Bei ca. 3.45 fängt die zweite Bifurkation an und es gibt nun 4 Häufungspunkte
Die Anzahl der Häufungspunkte der Folge/Population verdoppelt sich mit steigendem [math]r[/math] immer schneller, die nächste Verdopplung beginnt bei 3.54 . Ein Intervall, das durch 2 Bifurkationen begrenzt ist, wird dadurch immer kleiner.
Das Verhältnis der Längen zwei aufeinander folgender Intervalle konvergiert genau gegen die Feigenbaumkonstante δ ≈ 4,6692.
Fall [math]\boldsymbol{V}: 3,57 \le r \lt 4[/math]
nachdem sich die Anzahl der Häufungspunkte mit steigendem [math]r[/math] bis zu 3.57 immer schneller verdoppelt fängt ab 3.57 plötzlich Chaos an. Die Folgen konvergieren nicht mehr gegen eine endlich Anzahl an Häufungspunkten, sondern bleiben chaotisch. Bei diesen chaotischen Parametern spielt auch der Anfangswert wieder eine Rolle, da er nun maßgeblich die Folge bestimmt.
Es existieren jedoch auch in diesem Bereich nicht chaotische Parameter. In der Umgebung von 3.82 gibt es ein Intervall mit 3 Häufungspunkten, welches in ein kleineres Intervall mit 6 Häufungspunkten übergeht usw. , bis es wieder in Chaos übergeht. Tatsächlich kann man für jede beliebige Anzahl von Häufungspunkten in diesem Bereich ein Intervall finden.
Schlussendlich liegen die nicht chaotischen Parameter dicht in diesem Bereich, d.h. in jedem noch so kleinen Teilintervall aus diesem Bereich befinden sich Parameter, mit denen die Folge gegen eine endliche Anzahl an Häufungspunkten konvergiert
Fall [math]\boldsymbol{VI}: 4 ≤ r[/math]
Die Folge wächst monoton und überschreitet somit auch bei einem groß gewählten [math]n[/math] irgendwann die obere Populationsgrenze, und ist damit für Bevölkerungssimulationen nicht zu gebrauchen. Schlussendlich divergiert sie gegen [math]+ \infty[/math]
Die Berechnung der Feigenbaumkonstante
Ein Intervall ist ein Bifurkationsintervall, wenn für jedes [math]r[/math] aus dem Intervall die Folge [math](\boldsymbol{X}_{n})_{n\in\mathbb{N}}[/math] die gleiche Anzahl an Häufungspunkten besitzt
Beispielsweise ist [math]\lbrack 3, 3.45\rbrack[/math] ein Bifurkationsintervall, da jede die Folge [math](\boldsymbol{X}_{n})_{n\in\mathbb{N}}[/math] für jedes [math]r[/math] aus diesem Intervall 2 Häufungspunkte hat (vgl [math]\boldsymbol{III}[/math]), dies nennen wir [math]\boldsymbol{A}_1[/math] und jedes drauffolgende [math]\boldsymbol{A}_n[/math] ist das zugehörige Intervall der Strecke mit [math]2^n[/math] Häufungspunkten. Diese dabei entstande Folge ist eine monoton fallende Nullfolge, ihre Reihe konvergiert gegen einen Wert [math]\approx 0.57[/math], dies ist die Länge des in [math]\boldsymbol{III}[/math] und [math]\boldsymbol{IV}[/math] beschriebenen Bereichs.
Teilen wir die Länge zweier beliebiger benachbarter [math]\boldsymbol{A}_n[/math] dann kommt die schon oben erwähnte Feigenbaumkonstante raus.
%hier Bild einfügen der das Graphisch zeigt, am besten noch an zwei Stellen %Beispiel lässt sich hier gut durchrechnen mit A_2 und A_1 und A3 zu A2
[math]\frac{\boldsymbol{A}_n}{\boldsymbol{A}_{(n+1)}} = \delta \approx 4,6692[/math] Es ist tatsächlich egal ob wir das Verhältnis von [math]\boldsymbol{A}_1[/math] zu [math]\boldsymbol{A}_2[/math] betrachten oder von [math]\boldsymbol{A}_{1000}[/math] zu [math]\boldsymbol{A}_{1001}[/math], am Ende ergibt sich dabei immer die Feigenbaumkonstante. Sie ist auch nicht auf die logistische Gleichung beschränkt, sondern lässt sich beispielsweise auch errechnen in der Funktion [math]\boldsymbol{X}_{n+1}=\lambda*\sin(\boldsymbol{X}_n)[/math]
(#texen bild von dieser Funktion mit bsp. geogebra erstellen, danach die gleichen linien einfügen die in dem vorherigen Bild erstellt wurden)
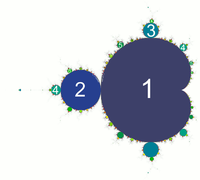
Bezug zum Mandelbrotset
Schaut man sich die einen beschränkte Bereiche der reellen Zahlen in der Mandelbrotmenge an, ist die Anzahl der Häufungspunkte in der Mandelbrotiteration und der logistischen Gleichung gleich.
Dieser Wert gilt für den gesamten Kardioid, in welchem die ursprungliche reelle Zahl enthalten war. Somit lassen sich die Anzahl der Häufungspunkte von Kardioiden berechnen, welche Teile der reellen Achse überdecken.
Die Feigenbaumkonstante ist also gleichzeitig auch das Längenverhältnis der Kardioiden des Mandelbrotsets.
_______________________________________________________________________________________________________________
NOCH UNERLEDIGTEs zeug
% Part 5: andere bezüge (veritasium vid. min 11) ?
sollten wir quellen brauchen, dann ist hier noch: https://de.wikipedia.org/wiki/Mandelbrot-Menge#Bezug_zur_Chaostheorie