Der kleine Satz von Fermat: Unterschied zwischen den Versionen
| Zeile 174: | Zeile 174: | ||
|''Wenn <math>n</math> eine Primzahl ist, dann hat das Polynom <math>X^2-1</math> über <math>\mathbb{Z}/n\mathbb{Z}</math> nur die beiden Wurzeln <math>x=1</math> und <math>x=-1</math>.'' | |''Wenn <math>n</math> eine Primzahl ist, dann hat das Polynom <math>X^2-1</math> über <math>\mathbb{Z}/n\mathbb{Z}</math> nur die beiden Wurzeln <math>x=1</math> und <math>x=-1</math>.'' | ||
|} | |} | ||
| − | Diese Aussage folgt direkt aus der Tatsache, dass die Anzahl der Nullstellen eines Polynoms über einem Körper höchstens gleich | + | Diese Aussage folgt direkt aus der Tatsache, dass die Anzahl der Nullstellen eines Polynoms über einem Körper höchstens gleich der Grad des Polynoms ist. Da <math>X^2-1</math> die beiden trivialen Wurzeln 1 und -1 über <math>\mathbb{Z}/n\mathbb{Z}</math> hat, gibt es keine weiteren Nullstellen. |
<br> | <br> | ||
<br> | <br> | ||
| − | + | Sei nun <math>2^s\cdot d+1</math> eine ungerade Primzahl, <math>s,d\in\mathbb{N}</math>, <math>d</math> ungerade und <math>a\in\mathbb{N},\ a<n</math>. | |
| + | <br> | ||
| + | Da <math>a<n</math> gilt nach dem ''Kleinen Satz von Fermat'': | ||
<br> | <br> | ||
: <math>a^{2^sd}\equiv1\ mod\ n</math> | : <math>a^{2^sd}\equiv1\ mod\ n</math> | ||
| Zeile 206: | Zeile 208: | ||
# Wurde eine Zahl <math>a</math> gefunden, für die <math>n</math> die Eigenschaft nicht erfüllt, so gebe “zusammengesetzt“ aus und stoppe das Verfahren. Wenn nicht, dann wiederhole die vorherigen Schritte, insgesamt nicht mehr als k mal. | # Wurde eine Zahl <math>a</math> gefunden, für die <math>n</math> die Eigenschaft nicht erfüllt, so gebe “zusammengesetzt“ aus und stoppe das Verfahren. Wenn nicht, dann wiederhole die vorherigen Schritte, insgesamt nicht mehr als k mal. | ||
Hat die gegebene Zahl beim k-maligen Durchlauf den Test bestanden, so gebe “wahrscheinlich prim“ aus.<br> | Hat die gegebene Zahl beim k-maligen Durchlauf den Test bestanden, so gebe “wahrscheinlich prim“ aus.<br> | ||
| − | Grundlegend für | + | Grundlegend für den angegebenen Algorithmus ist die Tatsache, dass jede Zahl, die keine starke Pseudoprimzahl zu einer beliebigen Basis <math>a</math> ist, keine Primzahl sein kann. Der Test besteht nun darin, zu der zu prüfenden Zahl <math>n</math> eine Basis <math>a</math> zu finden, so dass <math>n</math> keine starke Pseudoprimzahl zur Basis <math>a</math> ist und somit keine Primzahl. Findet man eine solche Zahl <math>a</math>, so nennt sich diese ein Zeuge der Zerlegbarkeit von <math>n</math>. |
<br> | <br> | ||
<br> | <br> | ||
Version vom 31. März 2021, 17:13 Uhr
Der kleine Satz von Fermat (auch: "Der kleine Fermat") ist ein Lehrsatz der Zahlentheorie und wurde im 17. Jahrhundert vom französischen Mathematiker Pierre de Fermat formuliert. Er macht folgende Aussage über Primzahlen:
Für jede ganze Zahl [math]a \in\mathbb{Z}[/math] und jede Primzahl [math]p[/math] gilt:
| [math] a^p\ \ mod\ p=a[/math] |
Dabei bedeutet mod „Teilen mit Rest“ : z.B. ist [math]10\ mod\ 7=3[/math], denn [math]10/7=1\ Rest\ 3[/math].
Auf den kleinen Satz von Fermat angewendet bedeutet dies, dass der Rest bei ganzzahliger Division von [math]a^{p}/ p[/math] genau [math]a[/math] ist. Dies ist gleichbedeutend damit, dass [math](a^p-a)\ mod\ p=0[/math], d.h. dass [math]p[/math] die Zahl [math]({a\ }^p\ – a)[/math] teilt.
Dies wird auch geschrieben als [math]p|a^p-a\ [/math].
Beweis
Erste Methode: Induktion
Bewiesen werden kann dieser Satz über vollständige Induktion nach [math]a[/math]:
Dabei werden zwei Fälle unterschieden:
1.Fall: [math]a\geq0[/math]
- Induktionsanfang: [math]a\ =\ 0[/math]
[math]p|a^p-a[/math] äquivalent zu [math]p|0^p-0[/math]
- Diese Aussage ist wahr für alle Primzahlen [math]p[/math], da jede ganze Zahl die [math]0[/math] teilt.
- Induktionsschritt:
- Es gelte für ein festes, aber beliebiges [math]a[/math] und alle Primzahlen [math]p[/math]: [math]p|a^p-a\ [/math]
- Nun ist zu zeigen, dass die Aussage auch für [math]a+1[/math] gilt, d.h [math]p|{(a+1)}^p-(a+1)[/math]
- Durch Anwenden des binomischen Lehrsatzes und anschließendes Herausziehen des ersten und letzten Summanden erhält man:
- [math]({a+1)\ }^p-(a+1)=\sum_{k=0}^{p\ }{\ \binom{p}{k}\ }a^{p-k}1^k-(a+1)\ [/math]
- [math]=\binom{p}{0}\ a^p\ \ +\ \ \ \sum_{k=1}^{p-1}{\ \binom{p}{k}}{\ a}^{p-k}+\binom{p}{p}a^0-a-1[/math]
- [math]=a^p\ \ +\ \ \ \sum_{k=1}^{p-1}{\ \binom{p}{k}}\ {\ a}^{p-k}+1-a-1[/math]
- [math]{=a}^p-a\ \ +\ \ \ \sum_{k=1}^{p-1}{\ \binom{p}{k}\ a}^{p-k}[/math]
- Der erste Summand ist nach Induktionsvoraussetzung bereits durch [math]p[/math] teilbar.Bleibt zu zeigen, dass auch der zweite Summand durch [math]p[/math] teilbar ist.
- Behauptung: [math]p|\binom{p}{k}[/math] für [math]1\le k\le p-1[/math]
- Nach Definition des Binomialkoeffizienten gilt:
[math]\binom{p}{k}\ =\frac{p!}{k!\ \left(p-k\right)!}[/math] äquivalent zu [math]\binom{p}{k}k!=\ \frac{p!}{\left(p-k\right)!}[/math]
- [math]\Rightarrow\frac{p!}{\left(p-k\right)!}=\frac{\left(p-k\right)\ \left(p-k+1\right)\ldots\left(p-1\right)\ p}{\left(p-k\right)!}=\left(p-k+1\right)\ldots\left(p-1\right)\ p[/math]
- [math]\Rightarrow p|\frac{p!}{\left(p-k\right)!}[/math] , da [math]p[/math] als Faktor vorkommt.
- Somit ist die rechte Seite der obigen Gleichung durch [math]p[/math] teilbar. Da [math]k \le p-1[/math] und [math]p[/math] eine Primzahl ist und somit insbesondere teilerfremd zu allen Zahlen kleiner gleich [math]p-1[/math], ist [math]k![/math] nicht durch [math]p[/math] teilbar. Folglich muss der Primfaktor [math]p[/math] also in [math]\binom{p}{k}\ [/math] enthalten sein, da Primfaktoren nicht „aufgespaltet“ werden können, d.h [math]\binom{p}{k}\ [/math] ist durch [math]p[/math] teilbar.
- Man erhält also insgesamt, dass von der Summe [math]a^p-a\ +\ \ \sum_{k=1}^{p-1}{\ \binom{p}{k}}{\ a}^{p-k}[/math] sowohl der erste Summand (nach Induktionsvoraussetzung) als auch jeder einzelne Summand des zweiten Summanden durch [math]p[/math] teilbar ist. Somit ist auch die ganze Summe durch [math]p[/math] teilbar.
2.Fall: [math]a\lt 0[/math]
- Wir schreiben [math]-a[/math] anstatt [math]a[/math]:
- [math]\Longrightarrow {(-a)}^p-(-a)={(-1)}^pa^p+a[/math]
- Für ungerade Primzahlen (also alle außer die [math]2[/math]) gilt dann:
- [math]\left(-a\right)^p-\left(-a\right)=-a^p+a=-(a^p-a)[/math]
- Für positive [math]a[/math] weiß man aber schon aus dem ersten Fall, dass [math]p|a^p-a\ [/math]. Somit gilt auch [math]{-p|-(a}^p-a)[/math].
- Falls [math]p = 2[/math]:
- [math]\left(-a\right)^p-\left(-a\right)=a^2+a=a\ \left(a+1\right)[/math]
- [math]\Longrightarrow p|{(-a)}^p-(-a)\ \Longleftrightarrow\ \ 2|a\ (a+1)[/math]
- Da von zwei aufeinanderfolgenden ganzen Zahlen immer genau eine gerade ist, gilt die Aussage.
Zweite Methode: Kombinatorik
Sei [math]p[/math] eine Primzahl und [math]a[/math] eine beliebige ganze Zahl. Nun soll aus Perlen mit [math]a[/math] verschiedenen Farben eine Kette mit [math]p[/math] Perlen gebildet werden. Also gibt es insgesamt [math]a^p[/math] Möglichkeiten wie die Kette aussieht.
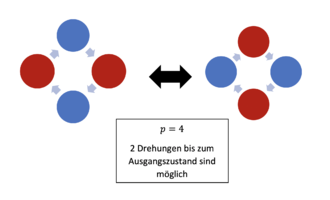
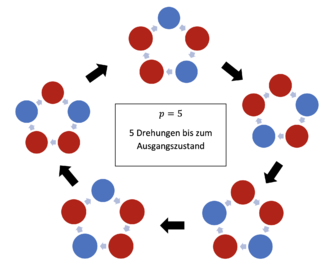
Wenn man nun eine beliebige Kette betrachtet, stellt man fest, dass man durch Drehen dieser, andere mögliche Ketten erhält, bis man spätestens nach [math]p[/math] Drehungen wieder bei der Ursprungskette landet. Es kann aber auch sein, dass man schon vorher wieder beim Anfangsmuster landet.
Beispiel: Bei einer Kette aus [math]p=4[/math] Perlen mit dem Muster rot-blau-rot-blau, wäre man nach zwei Drehungen schon wieder beim Ausgangsmuster.
Wir zeigen nun, dass wenn [math]p[/math] eine Primzahl ist, es aber nur zwei Möglichkeiten gibt nach welcher Anzahl an Drehungen man wieder am Anfang ist:
Sei [math]b[/math] also die kleinste Zahl, sodass man nach [math]b[/math]-maligem rotieren wieder die Anfangskette erhält.
Angenommen [math]b[/math] ist kein Teiler von [math]p[/math], dann sei [math]n\cdot\ b[/math] das kleinste Vielfache von [math]b[/math], sodass [math]n\cdot\ b\gt p[/math] gilt.
Daraus folgt aber auch: [math]0\lt n\cdot\ b-p\lt b[/math] und zudem überführt man die Kette durch [math]n\cdot\ b-p[/math]-maligem rotieren ebenfalls in den Anfangszustand zurück.
Das ist ein Widerspruch dazu, dass [math]b[/math] die kleinste Zahl ist, für die das möglich ist.
Daraus folgt, dass [math]b[/math] ein Teiler von [math]p[/math] sein muss. Da [math]p[/math] eine Primzahl ist, gilt also [math]b=1[/math] oder [math]b=p[/math].
Daraus ergeben sich also diese beiden Möglichkeiten für die Anfangskette:
- Alle Perlen besitzen dieselbe Farbe [math]\left(b=1\right)[/math]
- Es existiert mindestens eine andersfarbige Perle [math]\left(b=p\right)[/math]
Im ersten Fall lässt sich durch Rotation keine neue Kette bilden. Es gibt [math]a[/math] verschiedene solcher einfarbigen Ketten.
Also ist die Anzahl der gemischtfarbigen Ketten [math]a^p-a[/math].
Nach obiger Überlegung lassen sich diese aber in Gruppen zu je [math]p[/math] zusammenfassen und zwar je eine Anfangskette und die [math]p-1[/math] durch-Rotation-entstehenden Ketten (beim [math]p[/math]-ten Mal erhält man ja wieder die Ursprungskette). Also gilt, dass die Anzahl der gemischtfarbigen Ketten [math](a^p-a)[/math] durch [math]p[/math] teilbar ist, was zu zeigen war.
Fermat'scher Primzahltest
Folgerungen aus dem kleinen Satz von Fermat
- Wenn der Satz für eine Zahl [math]p[/math] nicht erfüllt ist, kann die Zahl [math]p[/math] auch keine Primzahl sein (Kontraposition des Satzes).
- Es folgt jedoch nicht, dass nur, weil eine Zahl [math]p[/math] diese Gleichung erfüllt, diese Zahl auch zwingend eine Primzahl ist. Denn der kleine Satz von Fermat ist nur eine Implikation in eine Richtung, die Rückrichtung gilt im Allgemeinen nicht:
Beispiel: [math]a = 4, p = 15 [/math]
[math]4^{15}\ \ mod\ 15=4[/math] , aber [math]15=5\cdot3[/math] ist keine Primzahl.
Diese Folgerungen bilden die Grundlage für viele Primzahltests. Ein Primzahltest, der den kleinen Satz von Fermat unmittelbar anwendet, hat folgendes Algorithmus.
Algorithmus
1. Schritt: Sei eine Zahl [math]p[/math], von der getestet werden soll, ob sie eine Primzahl ist.
2. Schritt: Berechne (beliebig oft) für zufällig gewählte [math]a[/math] den Ausdruck [math]{\ a}^p\ \ mod\ p[/math].
3. Schritt: Falls man dabei einmal als Ergebnis [math]{\ a}^p\ \ mod\ p\neq a[/math] erhält, so kann nach der zweiten Folgerung [math]p[/math] ganz sicher keine Primzahl sein.
4. Schritt: Falls das Ergebnis immer [math]a^p\ \ mod\ p=a[/math] ist, so lässt sich keine sichere Aussage treffen. Die zu testende Zahl erfüllt eine notwendige Bedingung dafür, prim zu sein, jedoch keine hinreichende. Die Aussage ist dann „wahrscheinlich prim“. Eine genaue Wahrscheinlichkeit kann dabei im Übrigen nicht angegeben werden.
Beispiele:
[math]a = 2, p = 3[/math]
[math]{{\ a}^p\ \ mod\ p=2}^3\ mod\ 3=8\ mod\ 3=\ 2[/math]
[math]\Longrightarrow 3[/math] ist „wahrscheinlich prim“.
[math]a = 2, p = 4[/math]
[math]{{\ a}^p\ \ mod\ p=2}^4\ mod\ 3=16\ mod\ 3=\ 1\neq2[/math]
[math]\Longrightarrow 4[/math] ist sicher keine Primzahl.
Bemerkung:
In der Praxis haben die zu testenden Zahlen meist mindestens mehrere hundert Stellen und für die Berechnung von [math]{\ a}^p\ \ mod\ p[/math] gibt es weitaus effizientere Möglichkeiten als zuerst die Potenz durch [math]p[/math]-malige Multiplikation von [math]a[/math] zu erhalten und dann modulo [math]p[/math] zu rechnen.
Carmichael Zahlen
Die offensichtliche Schwäche des obigen Tests ist es, dass er nicht mit absoluter Sicherheit sagen kann, ob eine Zahl prim ist. Das wäre in der Praxis nicht weiter schlimm, wenn es eine feste Irrtumswahrscheinlichkeit [math]P \lt 1[/math] gäbe. Dann müsste man den Test nur oft genug hintereinander mit zufällig gewählten a ausführen und durch die Potenzierung der Irrtumswahrscheinlichkeit könnte die insgesamte Irrtumswahrscheinlichkeit des Tests nach mehreren Durchläufen beliebig klein gemacht werden. Doch leider gibt es für den oben vorgestellten Test keine obere Schranke < 1 für die Irrtumswahrscheinlichkeit. Grund dafür sind die sogenannten Carmichael-Zahlen.
Diese haben folgende Eigenschaft: Sie erfüllen den obigen Primzahltest für alle Basen [math]a[/math], die teilerfremd zu der Carmichael-Zahl [math]p[/math] sind, d.h. der größte gemeinsame Teiler von [math]a[/math] und [math]p[/math] muss 1 sein.
Die kleinste Carmichael-Zahl ist [math]561 = 3 \cdot11\ \cdot17[/math].
D.h. für alle Basen [math]a[/math], die in ihrer Primfaktorzerlegung weder die 3 noch die 11 noch die 17 enthalten, gilt: [math]{\ a}^{561}\ \ mod\ 561 = a[/math].
Insbesondere für Carmichael-Zahlen mit größeren Primfaktoren (die 3 bildet hier eine Ausnahme) ist dann die Wahrscheinlichkeit, dass beim Ausführen des obigen Tests mit z.B. 10 verschiedenen [math]a[/math] jedes Mal „wahrscheinlich prim“ und somit auch insgesamt „wahrscheinlich prim“ herauskommt, sehr hoch, obwohl es sich nicht um eine Primzahl handelt.
Die Carmichael-Zahlen werden deshalb auch fermatsche Pseudoprimzahlen genannt.
Von diesen Carmichael-Zahlen gibt es zwar nur „wenige“, aber doch unendlich viele (auf den Beweis verzichten wir an dieser Stelle), d.h. in unendlich vielen Fällen liefert der obige Test höchstwahrscheinlich ein falsches Ergebnis.
Um diese unschöne Eigenschaft zu vermeiden, gibt es den sogenannten Miller-Rabin-Test, der vor allem in der Kryptographie zum Einsatz kommt und im nächsten Abschnitt vorgestellt wird.
Der Miller-Rabin Test
Der Miller-Rabin Test ist ein probabilistischer Primzahltest, der als optimierte Version des klassischen Primzahltestes betrachtet werden kann. Ähnlich wie der Fermat’sche Test wird überprüft, ob eine Eigenschaft von Primzahlen auch für eine gegebene Zahl gilt. Dafür definiert man zuerst die starken Pseudoprimzahlen.
Starke Pseudoprimzahlen
Sei [math]n\gt 2[/math] eine natürliche, ungerade Zahl. [math]n[/math] lässt sich eindeutig schreiben als [math]2^s\cdot d+1[/math], wobei [math]s,d[/math] natürliche Zahlen sind und [math]d[/math] ungerade. Sei nun [math]a\lt n[/math] eine natürliche Zahl. Man nennt [math]n[/math] eine starke Pseudoprimzahl zur Basis [math]a[/math], wenn [math]n[/math] eine der folgenden Bedingungen erfüllt:
- [math]a^d\equiv1\ mod\ n[/math]
- [math]a^{2^rd}\equiv-1\ mod\ n[/math] für eine beliebige, natürliche Zahl [math]0\le\ r\lt s[/math]
Betrachten wir folgende zwei Beispiele zur Veranschaulichung:
1. Beispiel
[math]n=121[/math] ist eine starke Pseudoprimzahl zur Basis [math]a=3[/math], denn:
[math]n=2^3\cdot15+1[/math], also gilt [math]s=3[/math] und [math]d=15[/math].
Man merkt, dass die erste Bedingung erfüllt wird, da [math]3^{15}\equiv1\ mod\ 121[/math] gilt.
2. Beispiel
[math]n=325[/math] ist eine starke Pseudoprimzahl zur Basis [math]a=7[/math], denn:
[math]n=2^2\cdot81+1[/math], also gilt [math]s=2[/math] und [math]d=81[/math].
Man stellt fest, dass die erste Bedingung nicht erfüllt wird: [math]7^{81}\ mod\ 325=307\neq1[/math] (in diesem Fall ist [math]r=0[/math])
Wir überprüfen nun, dass die zweite Bedingung tatsächlich erfüllt wird:
[math]0\le r\lt s=2[/math], also [math]r\in\left\{0,\ 1\right\}[/math].
Für [math]r=0[/math] gilt: [math]7^{81}\ mod\ 325=307\neq-1[/math]
Für [math]r=1[/math] gilt: [math]7^{2^1\cdot81}\ mod\ 325=7^{162}\ mod\ 325=324=-1[/math]
Somit ist die zweite Bedingung für [math]r=1[/math] erfüllt.
Lemma
| Jede Primzahl ist auch eine starke Pseudoprimzahl zu jedwelcher Basis. |
Beweis: Eine notwendige Erkenntnis für den Beweis des Lemmas ist folgende:
| Wenn [math]n[/math] eine Primzahl ist, dann hat das Polynom [math]X^2-1[/math] über [math]\mathbb{Z}/n\mathbb{Z}[/math] nur die beiden Wurzeln [math]x=1[/math] und [math]x=-1[/math]. |
Diese Aussage folgt direkt aus der Tatsache, dass die Anzahl der Nullstellen eines Polynoms über einem Körper höchstens gleich der Grad des Polynoms ist. Da [math]X^2-1[/math] die beiden trivialen Wurzeln 1 und -1 über [math]\mathbb{Z}/n\mathbb{Z}[/math] hat, gibt es keine weiteren Nullstellen.
Sei nun [math]2^s\cdot d+1[/math] eine ungerade Primzahl, [math]s,d\in\mathbb{N}[/math], [math]d[/math] ungerade und [math]a\in\mathbb{N},\ a\lt n[/math].
Da [math]a\lt n[/math] gilt nach dem Kleinen Satz von Fermat:
- [math]a^{2^sd}\equiv1\ mod\ n[/math]
Betrachtet man die Folge [math]a^{2^sd},\ \ a^{2^{s-1}d},\ \ldots,\ \ a^{2d},\ a^d[/math] so merkt man, dass jedes Glied, außer dem ersten, die Wurzel des vorherigen Folgengliedes ist. Da
| [math]a^{2^sd}-1=\left(a^{2^{s-1}d}\right)^2-1\equiv0\ \ mod\ n[/math] |
| gilt: | [math]a^{2^{s-1}d}\equiv1\ mod\ n\ \ \left(1\right)[/math] | oder | [math]a^{2^{s-1}d}\equiv-1\ \ mod\ n\ \ \left(2\right)[/math] |
Falls [math]\left(2\right)[/math] richtig ist, so ist die zweite Bedingung bereits erfüllt mit [math]r=s-1[/math]. Falls [math]\left(1\right)[/math] richtig ist, so wendet man wiederholt dieselben Schritte an bis entweder eins der Glieder kongruent modulo [math]n[/math] mit [math]-1[/math] ist oder alle Folgenglieder, insbesondere der letzte, kongruent modulo [math]n[/math] mit [math]1[/math] sind.
Der Miller-Rabin Test
Mittels der vorher bewiesenen Eigenschaft der Primzahlen ergibt sich folgender Algorithmus, bekannt als der Miller-Rabin Test:
Eingaben:
- eine natürliche, ungerade Zahl n, die getestet wird
- eine natürliche Zahl k, die die Anzahl der Wiederholungen des Testes angibt
Ausgabe:
- „zusammengesetzt”, wenn n nicht prim ist
- „wahrscheinlich prim“ sonst
Schritte:
- Schreibe [math]n[/math] als [math]2^s\cdot d+1[/math] mit [math]s,d\in\mathbb{N}[/math], [math]d[/math] ungerade.
- Wähle eine Zahl [math]a\in\left\{1,\ \ldots,\ \ n-1\right\}[/math] zufällig und gleichverteilt.
- Teste ob [math]n[/math] eine starke Pseudoprimzahl zur Basis [math]a[/math] ist.
- Wurde eine Zahl [math]a[/math] gefunden, für die [math]n[/math] die Eigenschaft nicht erfüllt, so gebe “zusammengesetzt“ aus und stoppe das Verfahren. Wenn nicht, dann wiederhole die vorherigen Schritte, insgesamt nicht mehr als k mal.
Hat die gegebene Zahl beim k-maligen Durchlauf den Test bestanden, so gebe “wahrscheinlich prim“ aus.
Grundlegend für den angegebenen Algorithmus ist die Tatsache, dass jede Zahl, die keine starke Pseudoprimzahl zu einer beliebigen Basis [math]a[/math] ist, keine Primzahl sein kann. Der Test besteht nun darin, zu der zu prüfenden Zahl [math]n[/math] eine Basis [math]a[/math] zu finden, so dass [math]n[/math] keine starke Pseudoprimzahl zur Basis [math]a[/math] ist und somit keine Primzahl. Findet man eine solche Zahl [math]a[/math], so nennt sich diese ein Zeuge der Zerlegbarkeit von [math]n[/math].
Für zusammengesetzte Zahlen [math]n[/math] lässt sich immer wenigstens ein Zeuge ihrer Zerlegbarkeit finden, aber nicht alle Zahlen [math]a[/math] eignen sich dazu (siehe das erste Beispiel). Daher muss man [math]n[/math] für mehrere Basen testen. Besteht die Zahl [math]n[/math] bei jedem Durchlauf den Test, so kann nur eine Wahrscheinlichkeitsaussage getroffen werden. Die Fehlerwahrscheinlichkeit, also die Wahrscheinlichkeit, dass die getestete Zahl keine Primzahl ist, nimmt ab je häufiger die Zahl [math]n[/math] den Test besteht. In der Praxis testet man die Zahl [math]n[/math] auf hinreichend vielen Basen [math]a[/math], so dass die Fehlerwahrscheinlichkeit vernachlässigbar klein ist.
Beispiele
I. Führen wir nun den Test [math]k=2[/math] mal für die Zahl [math]n=221[/math] durch.
- 1. Schritt: [math]n-1=220=2^2\cdot55\ \ \ \ [/math]
- Also [math]s=2[/math] und [math]d=55[/math].
Erster Durchlauf:
- 2. Schritt: Wir wählen die Basis [math]a=174[/math].
- 3. Schritt: Wir testen, ob [math]n[/math] eine starke Pseudoprimzahl zur Basis [math]a[/math] ist:
- [math]a^d\ mod\ n={174}^{55}\ mod\ 221=47\ \neq-1\ und\ \neq1[/math]
- [math]a^{2d}\ mod\ n={174}^{110}\ mod\ 221=220=-1[/math]
- Für [math]r=1[/math] gilt also [math]a^{2^rd}\equiv-1\ mod\ n[/math], also könnte [math]221[/math] prim sein.
Zweiter Durchlauf:
- 2. Schritt: Wir wählen die Basis [math]a=137[/math].
- 3. Schritt: Wir testen, ob [math]n[/math] eine starke Pseudoprimzahl zur Basis [math]a[/math] ist:
- [math]a^d\ mod\ n={137}^{55}\ mod\ 221=188\neq-1\ und\ \neq1[/math]
- [math]a^{2d}\ mod\ n={137}^{110}\ mod\ 221=205\neq-1[/math]
- [math]a=137[/math] ist ein Zeuge der Zerlegbarkeit von [math]n=221[/math], also ist [math]221[/math] keine Primzahl.
II. Im Unterschied zu dem Fermat’schen Primzahltest filtert der Miller-Rabin Test auch die Carmichaelzahlen aus.
Betrachten wir dafür die kleinste Carmichaelzahl [math]n=561[/math]. Wir führen den Test ein einziges Mal durch und wählen als Basis [math]a=2[/math].
- 1.Schritt: [math]n-1=560=2^4\cdot35[/math]
- Also [math]s=4[/math] und [math]d=35[/math].
- 2. Schritt: [math]a=2[/math]
- 3. Schritt: Wir testen, ob [math]n[/math] eine starke Pseudoprimzahl zur Basis [math]a[/math] ist:
- [math]a^d\ mod\ n=2^{35\ }\ mod\ \ 561=263\neq-1\ und\ \neq1[/math]
- [math]a^{2d}\ mod\ n=2^{70}\ mod\ 561=166\neq-1[/math]
- [math]a^{2^2d}\ mod\ n=2^{140}\ mod\ 561=67\neq-1[/math]
- [math]a^{2^3d}\ mod\ n=2^{280}\ mod\ 561=1\neq-1[/math]
Somit erfüllt [math]n=561[/math] für die Basis [math]a=2[/math] keine der beiden Bedingungen einer starken Pseudoprimzahl und ist daher auch keine Primzahl.
Quellen
- http://www.austromath.at/medienvielfalt/materialien/krypto/lernpfad/content/k_prim_l06.htm
- https://en.wikipedia.org/wiki/Miller%E2%80%93Rabin_primality_test
- http://page.math.tu-berlin.de/~kant/teaching/hess/krypto-ws2007/miller-rabin.pdf
- https://www.youtube.com/watch?v=YqHZQmbDw6s
- https://de.wikibooks.org/wiki/Beweisarchiv:_Zahlentheorie:_Elementare_Zahlentheorie:_Kleiner_Satz_von_Fermat