Magische Quadrate: Unterschied zwischen den Versionen
| Zeile 1: | Zeile 1: | ||
==Definition== | ==Definition== | ||
[[Datei:Bild1.png|mini|102x102px]] | [[Datei:Bild1.png|mini|102x102px]] | ||
| − | Ein magisches Quadrat der Ordnung n beschreibt eine n×n Matrix, in welcher ganze Zahlen, häufig 1,..., <math>n^2 </math>, so angeordnet sind, dass die Summe der Zeilen- und Spalteneinträgen dem gleichen Wert entspricht. Diesen nennt man die magischen Summe. Die summierten Einträge der Hauptdiagonalen sind ebenfalls gleich der magischen Summe. | + | Ein magisches Quadrat der Ordnung n beschreibt eine n×n Matrix, in welcher paarweise verschiedene ganze Zahlen, häufig 1,..., <math>n^2 </math>, so angeordnet sind, dass die Summe der Zeilen- und Spalteneinträgen dem gleichen Wert entspricht. Diesen nennt man die magischen Summe. Die summierten Einträge der Hauptdiagonalen sind ebenfalls gleich der magischen Summe. |
Man spricht von einem semimagischen Quadrat, falls die Hauptdiagonalen nicht der magischen Summe entsprechen. | Man spricht von einem semimagischen Quadrat, falls die Hauptdiagonalen nicht der magischen Summe entsprechen. | ||
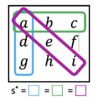
<br />Für die Einträge <math> 1,.., n^2 </math> entspricht die magische Summe <math> s^* = \frac{1}{n} \sum\limits_{k=1}^{n^2} k</math>. | <br />Für die Einträge <math> 1,.., n^2 </math> entspricht die magische Summe <math> s^* = \frac{1}{n} \sum\limits_{k=1}^{n^2} k</math>. | ||
| + | == magische Quadrate niedriger Ordnung == | ||
| + | Im folgenden betrachten wir magische Quadrate mit niedriger Ordnung. Da durch komponentenweise Addition zweier magischer Quadrate und der Multiplikation mit einem Skalar sich nur die magische Summer ändert, aber die Eigenschaft des magischen Quadrats erhalten bleibt betrachten wir im folgenden nur ??? magische Quadrate. | ||
| + | === magische Quadrate 1-ter Ordnung === | ||
| + | Magische Quadrate erster Ordnung besitzen nur einen Eintrag und sind somit trivial, da jeden 1×1-Matrix die EIgenschaft eines magischen Quadrates erfüllt. | ||
| + | === magische Quadrate 2-ter Ordnung === | ||
| + | Nach der oben aufgeführten Definition von magischen existieren keine magischen Quadrate zweiter Ordnung. Vernachlässigt man die Bedingung der paarweise verschiedenen Einträge haben magische bzw. semimagische Quadrate folgende Form | ||
| + | <math> | ||
| + | \text{magisches Quadrat 2-ter Ordnung} | ||
| + | \begin{bmatrix} | ||
| + | a & a \\ | ||
| + | a & a \\ | ||
| + | \end{bmatrix} | ||
| + | text{magisches Quadrat 2-ter Ordnung} | ||
| + | \begin{bmatrix} | ||
| + | a & b \\ | ||
| + | b & a\\ | ||
| + | \end{bmatrix} | ||
| + | </math> | ||
| + | === magische Quadrate 3-ter Ordnung === | ||
== Weblinks == | == Weblinks == | ||
Version vom 25. August 2021, 07:41 Uhr
Definition
Ein magisches Quadrat der Ordnung n beschreibt eine n×n Matrix, in welcher paarweise verschiedene ganze Zahlen, häufig 1,..., [math]n^2 [/math], so angeordnet sind, dass die Summe der Zeilen- und Spalteneinträgen dem gleichen Wert entspricht. Diesen nennt man die magischen Summe. Die summierten Einträge der Hauptdiagonalen sind ebenfalls gleich der magischen Summe.
Man spricht von einem semimagischen Quadrat, falls die Hauptdiagonalen nicht der magischen Summe entsprechen.
Für die Einträge [math] 1,.., n^2 [/math] entspricht die magische Summe [math] s^* = \frac{1}{n} \sum\limits_{k=1}^{n^2} k[/math].
magische Quadrate niedriger Ordnung
Im folgenden betrachten wir magische Quadrate mit niedriger Ordnung. Da durch komponentenweise Addition zweier magischer Quadrate und der Multiplikation mit einem Skalar sich nur die magische Summer ändert, aber die Eigenschaft des magischen Quadrats erhalten bleibt betrachten wir im folgenden nur ??? magische Quadrate.
magische Quadrate 1-ter Ordnung
Magische Quadrate erster Ordnung besitzen nur einen Eintrag und sind somit trivial, da jeden 1×1-Matrix die EIgenschaft eines magischen Quadrates erfüllt.
magische Quadrate 2-ter Ordnung
Nach der oben aufgeführten Definition von magischen existieren keine magischen Quadrate zweiter Ordnung. Vernachlässigt man die Bedingung der paarweise verschiedenen Einträge haben magische bzw. semimagische Quadrate folgende Form [math] \text{magisches Quadrat 2-ter Ordnung} \begin{bmatrix} a & a \\ a & a \\ \end{bmatrix} text{magisches Quadrat 2-ter Ordnung} \begin{bmatrix} a & b \\ b & a\\ \end{bmatrix} [/math]
magische Quadrate 3-ter Ordnung
Weblinks
Einzelnachweise/Literaturverzeichnis
Beck, Matthias; Robins, Sinai: Das Kontinuum diskret berechnen. Kapitel 6.
Sesiano, Jacques: Magic Squares-Their History and Construction from Ancient Times to AD 1600.
AutorInnen
Julia Renner
Joanna Schnorr
Julia Bohn
Vorlage
Überschrift 1
Überschrift 2
Hier kann man ganz normal schreiben :)
[math] \text{hier müsste es wie in der Latex equation-Funktion Formeln schreiben können } x \in \mathbb{N} : x \in \mathbb{R} [/math]
- nummerierte Aufzählungen
- neue Ebene
- usw.
- neue Ebene
- Aufzählung mit Punkt
- tiefere Ebene
- - Was passiert hier
- Aufzählung ohne Zeichen
- Unterpunkt
- Aufzählung 2 ohne Zeichen
Hier wird etwas wichtiges zitiert
hier könnte Ihr eingerückter Text stehen
unterstrichen durchgestrichen
Durch diesen Befehl kann
innerhalb eines Absatz ein Zeilenumsprung erzeugt werden