Normen und Metriken: Unterschied zwischen den Versionen
| Zeile 97: | Zeile 97: | ||
== Hierarchie Topologischer Räume == | == Hierarchie Topologischer Räume == | ||
| − | [[Datei:1200px-Beziehungen zwischen mathematischen Räumen.svg.png|mini|Hierarchie topologischer Räume]] | + | [[Datei:1200px-Beziehungen zwischen mathematischen Räumen.svg.png|mini|160x160px|Hierarchie topologischer Räume]] |
Wie gesehen, ist induziert jede Norm eine Metrik, somit ist jeder normierte Vektorraum auch ein metrischer Raum. Analog dazu induziert jedes Skalarprodukt <math> (\cdot,\cdot) </math> eine Norm via <math> \left\Vert v \right\Vert = \sqrt{(v.v)} </math>. | Wie gesehen, ist induziert jede Norm eine Metrik, somit ist jeder normierte Vektorraum auch ein metrischer Raum. Analog dazu induziert jedes Skalarprodukt <math> (\cdot,\cdot) </math> eine Norm via <math> \left\Vert v \right\Vert = \sqrt{(v.v)} </math>. | ||
Außerdem induziert jede Metrik auf dem metrischen Raum <math> (M,d) </math> eine Topologie via <math> \ \mathcal{O} := \{U \subset M, U\ \text{ist offen bzgl.}\ d\}. </math> | Außerdem induziert jede Metrik auf dem metrischen Raum <math> (M,d) </math> eine Topologie via <math> \ \mathcal{O} := \{U \subset M, U\ \text{ist offen bzgl.}\ d\}. </math> | ||
Version vom 19. September 2021, 16:41 Uhr
Eine Norm ist eine Abbildung, die auf einem Vektorraum definiert ist und jedem Objekt in diesem Vektorraum eine reelle Zahl zuordnet, die die Größe des Objekts beschreiben soll. Eine Metrik ist auf einer Menge definiert und ordnet je zwei Punkten eine reelle Zahl zu, die gewissermaßen den Abstand der Punkte abgibt.
Normen und Metriken sind nicht eindeutig auf dem Vektorraum bzw. der Menge definiert und so ist es durchaus möglich, dass bspw. unterschiedliche Normen dem gleichen Objekt eine andere Größe zuordnen. Dennoch erfüllen Normen und Metriken drei definierende Eigenschaften, und grundlegende Konzepte wie bspw. Konvergenz sind unabhängig von der gewählten Norm bzw. Metrik
Motivation
Unser Ziel ist es, mathematischen Objekten eine gewisse Größe und einen gewissen Abstand zuzuordnen. Aus den reellen Zahlen kennen wir bereits den Absolutbetrag und die absolute Differenz. Dieses Konzept möchten wir abstrahieren und so allgemein wie möglich formulieren, sprich auch einen Abstands- und Größenbegriff für Vektorräume oder idealerweise allgemeine Mengen definieren. Den Größenbegriff werden wir dann als Norm bezeichnen, den Abstandsbegriff als Metrik.
Wir werden feststellen, dass wir Normen auf vielen Vektorräumen definieren können und somit einen Größenbegriff für bspw. Vektoren und Matrizen, aber auch für weniger intuitive Dinge wie Funktionen erhalten. Metriken können wir sogar auf allgemeinen Mengen definieren, ohne eine Vektorraumstruktur zu benötigen.
Norm
Definition
Eine Norm ist eine Abbildung [math]\|\cdot\|[/math] von einem Vektorraum [math]V[/math] über dem Körper [math]\mathbb K[/math] der reellen oder komplexen Zahlen in die Menge der nichtnegativen reellen Zahlen [math]{\mathbb R}_0^{+}[/math],
- [math]\|\cdot\|\colon V\to{\mathbb R}_0^{+}, \; x \mapsto \| x \|[/math],
welche die folgenden Axiome für alle Vektoren [math]x, y\in V[/math] und alle Skalare [math]\alpha\in\mathbb K[/math] erfüllt:
| N1 Definitheit: | [math]\|x\| = 0 \;\Rightarrow\; x = 0[/math], |
| N2 Homogenität: | [math]\|\alpha\cdot x\| = |\alpha|\cdot\|x\|[/math], |
| N3 Dreiecksungleichung: | [math]\|x + y\| \leq \|x\| + \|y\|[/math]. |
Grundlegende Eigenschaften
Aus der Homogenität folgt:
- [math]x = 0 \;\Rightarrow\; \| x \| = 0[/math]
Zusammen mit der Definitheit gilt also, dass ein Vektor genau dann die Norm Null hat, wenn er der Nullvektor ist.
Die Symmetrie bezüglich Vorzeichen folgt ebenfalls aus der Definitheit durch Einsetzen von [math]\alpha = -1[/math]:
- [math]\| {-x} \| = \| x \|[/math] und damit [math]\| x-y \| = \| y-x \|[/math]
Mithilfe der der Dreiecksungleichung folgt dann: Setze [math]y = -x[/math],
[math]0= \|x + (-x)\| \leq \|x\| + \|-x\| = 2\| x \| \;\Rightarrow\; \| x \| \geq 0 [/math], also eine Norm ist immer nichtnegativ
Äquivalenz von Normen
Zwei Normen sind äquivalent, wenn eine Norm durch die andere nach oben und unten abgeschätzt werden kann,
es gibt also zwei positive Konstanten [math]c_1[/math] und [math]c_2[/math] gibt, sodass für alle [math]x \in V[/math] folgendes gilt:
- [math]c_1 \|x\|_b\leq \|x\|_a\leq c_2 \|x\|_b[/math]
Metrik
Definition
Sei [math]X[/math] eine Menge. Eine Abbildung [math]d\colon X\times X\to \mathbb{R}[/math] heißt Metrik auf [math]X[/math], falls folgenden Eigenschaften für beliebige [math]x[/math], [math]y[/math] und [math]z[/math] von [math]X[/math] gelten:
| M1 Positive Definitheit: | [math]d\left(x,y\right) \geq 0[/math] und [math]d\left(x,y\right) = 0 \Leftrightarrow x = y[/math], |
| M2 Symmetrie: | [math]d\left(x,y\right) = d(y,x)[/math], |
| M3 Dreiecksungleichung: | [math]d\left(x,y\right) \leq d(x,z) + d(z,y)[/math]. |
das Paar ([math]X[/math],d) nennt man metrischer Raum.
Bemerkung
Für eine Metrik [math]d[/math] gilt stets:
[math]d(x,y)\geq0[/math]
| AusklappenBeweis |
Zusammenhang von Norm und Metrik
In den reellen Zahlen wird bekanntermaßen der Absolutbetrag einer Zahl als Abstand der Zahl von 0 definiert, sprich
- [math] |x| = \begin{cases} x & \text{falls}\ x \geq 0 \\ -x & \text{falls}\ x \lt 0 \end{cases}\ , \ x \in \mathbb{R} [/math],
die absolute Differenz durch
- [math] d(x,y) = |x-y| , \ \ x,y \in \mathbb{R} [/math].
Dass der Absolutbetrag somit auch in der Definition unseres Abstandes in den reellen Zahlen vorkommt, legt bereits nahe, dass Normen und Metriken nicht zwei zusammenhangslose Konzepte sind, sondern, dass es eine Verbindung zwischen ihnen gibt und tatsächlichen werden wir sehen, dass sehr viele Metriken durch zugrundeliegende Normen definiert werden können ("von Normen induziert werden").
Induzierte Metriken
Es sei [math] \left\Vert \cdot \right\Vert [/math] eine Norm auf einem Vektorraum. Dann definiert [math] d(x, y) := \left\Vert x - y \right\Vert [/math] eine Metrik.
Beweis
M1 [math] d(x,y) = 0 \Leftrightarrow \left\Vert x - y \right\Vert = 0 \Leftrightarrow x-y = 0 \Leftrightarrow x = y [/math]
M2 [math] d(x,y) = \left\Vert x - y \right\Vert = \left\Vert (-1)(y-x) \right\Vert = \left\vert -1 \right\vert \left\Vert y-x \right\Vert = d(y,x) [/math]
M3 [math] d(x,z) = \left\Vert x - z \right\Vert = \left\Vert x - y + y - z \right\Vert \le \left\Vert x - y \right\Vert + \left\Vert y - z \right\Vert = d(x,y)+d(y,z) [/math]
Somit besitzt jeder normierte Vektorraum auch eine Metrik, ist also auch ein normierter Raum.
Im Gegensatz dazu, ist nicht jeder normierte Vektorraum auch ein metrischer Raum, s. Beispiele
Hierarchie Topologischer Räume
Wie gesehen, ist induziert jede Norm eine Metrik, somit ist jeder normierte Vektorraum auch ein metrischer Raum. Analog dazu induziert jedes Skalarprodukt [math] (\cdot,\cdot) [/math] eine Norm via [math] \left\Vert v \right\Vert = \sqrt{(v.v)} [/math]. Außerdem induziert jede Metrik auf dem metrischen Raum [math] (M,d) [/math] eine Topologie via [math] \ \mathcal{O} := \{U \subset M, U\ \text{ist offen bzgl.}\ d\}. [/math] Somit erhält man die folgende Hierarchie metrischer Räume:
Metrik Beispiele
Durch Normen induzierte Metriken
Jede Norm die es auf einem Vektorraum gibt induziert wie folgt eine Metrik
- [math]d(x, y) \equiv \|x - y\|[/math]
Daher sehen wir, dass jeder normierte VR ein metrischer Raum ist.
- Ein weiteres Beispiel ist:
Die euklidische Metrik
In der zweidimensionalen euklidischen Ebene stimmt der euklidische Abstand [math]d(x,y)[/math] mit dem gängigen Gedanken des Abstandes überein.
Sind die Punkte [math]x[/math] und [math]y[/math] durch [math]x=(x_1, \ldots, x_n)[/math] und [math]y=(y_1, \ldots, y_n)[/math] gegeben, so definieren wir die euklidische Metrik wie folgt:
- [math]d(x,y) = \|x-y\|_2 =\sqrt{(x_1 - y_1)^2 + \cdots + (x_n - y_n)^2} = \sqrt{\sum_{i=1}^n (x_i-y_i)^2}[/math]
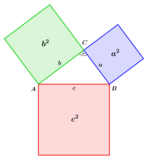
Dies kennen wir aus der Schulmathematik für n=2 als Satz des Phythagoras. Der euklidische Abstand ist eine Metrischer Raum welcher die Dreiecksungleichung erfüllt und die Axiome einer Norm erfüllt, somit durch eine Norm induziert.
Nicht durch Normen induzierte Metriken
Es gibt Metriken welche nicht die Axiome N1-N3 einer Norm nicht erfüllen ein Beispiel hierfür ist folgende Metrik welche das Axiom N2 nicht erfüllt:
Die Diskrete Metrik
Auf jeder menge lässt sich die triviale Metrik definieren, sie wird auch diskrete Metrik gennant und ist dazu noch eine Ultrametrik.
- Sie wird wie folgt definiert:
- Sei [math]X[/math] eine Menge, [math]x[/math],[math]y[/math] aus [math]X[/math] und [math]d[/math] eine Abbildung [math] d\colon X\times X\to\mathbb R [/math] mit
- [math]d(x,y)=\begin{cases} 0 & \text{für } x = y \\ 1 & \text{für } x\neq y \end{cases}[/math]
Diese Metrik induziert die diskrete Topologie.
Ein weiteres Beispiel, welche nicht alle Axiome einer Norm erfüllt, ist die:
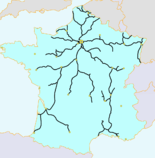
Die SNCF-Metrik
Sei [math]X[/math] eine Menge von Punkten in der Ebene und [math] p [/math] ein fester Punkt.
Dann ist die SNCF-Metrik auf [math]X[/math] wie folgt definiert:
- [math] d\colon X\times X\to\mathbb R [/math]
- [math] d(x,y)=\begin{cases} \|x-y\|&\text{falls } x, y \text{ auf einer Geraden durch } p \text{ liegen, }\\ \|x-p\|+\|p-y\|&\text{sonst}. \end{cases} [/math]
Der Name dieser Metrik leitet sich von der Eisenbahngesellschaft SNCF ab, da diese Metrik in den Kontext des Französischen Eisenbahnnetzes fällt.
Nehme man an X seien die Städte Frankreichs, und [math] p [/math] Paris so kann der Abstand, falls es keinen direkt Zug zwischen der Stadt [math]x[/math] und [math]y[/math] gibt, deutlich länger werden.
Spezielle Metriken
Ultrametrik
Eine Metrik nennt man Ultrametrik falls bei der M3 Dreiecksungleichung gilt, dass der Abstand [math]d(x, y)[/math] nicht länger ist als der längere der beiden Abstände [math]d(x, z)[/math] und [math]d(z, y)[/math] ist und das mit beliebigem [math]z[/math]. Beispielsweise die Diskrete Metrik.
Pseudometrik
Stellt eine Metrik dar in welcher die Bedingung aus M1 [math]d\left(x,y\right) = 0 \Rightarrow x = y[/math] nicht gilt, somit ist sie positive semidefinit. Sie wird in der Funtkionalanalysis auch als Halb- oder Semimetrik bezeichnet.
Nicht-archimedische Metriken
Hier wird die M3 Dreiecksungleichung verstärkt oder geschwächt. Ein Beispiel für diese Metrik wäre die Ultrametrik.
Quasimetrik
Verzichtet man auf M2 (Symmetrie) der Axiome so erhält man eine Quasimetrik. Eine Quasimetrik [math]b[/math] erzeugt durch [math]d(x,y):= \tfrac{1}{2} ( b(x,y) + b(y,x) )[/math] eine Metrik auf [math]X[/math].
Prämetrik
Die Prämetrik fordert nur das Axiom M1 (Positive Definitheit).
Norm Beispiele
Normen auf endlichdimensionalen Vektorräumen
Die Betragsnorm
Der Betrag ist das einfachste und am häufigsten auftretende Beispiel einer Norm. Man erhält ihn durch Weglassen des Vorzeichens:
- [math]\| z \| = | z | = \begin{cases} \,\ \ z &\mathrm{f\ddot ur}\ z \ge 0\\ \, -z &\mathrm{f\ddot ur}\ z \lt 0. \end{cases} [/math]
Bei komplexen Zahlen ist der Betrag definiert durch:
- [math]\| z \| = | z | = \sqrt{\left(\operatorname{Re} z\right)^2 + \left(\operatorname{Im} z\right)^2}[/math]
Euklidische Norm
Die euklidische Norm eines Vektors, auch 2-Norm eines Vektors genannt ist definiert als
- [math]\| x \|_2 = \sqrt{\sum_{i=1}^n |x_i|^2}[/math],
wobei mit [math]x_i[/math] die einzelnen Komponenten eines Vektors gemeint sind.
Maximumsnorm
Die Maximumsnorm (auch Unendlich-Norm genannt) eines Vektors ist definiert als
- [math]\| x \|_{\infty} = \max_{i=1, \dotsc, n} |x_i|[/math]
Summennorm
Die Summennorm (auch 1-Norm genannt) eines Vektors ist definiert als
- [math]\| x \|_1 = \sum_{i=1}^n | x_i |[/math]
Äquivalenz von Normen in endlichdimensionalen Räumen
Normen auf unendlichdimensionalen Vektorräumen
Operatornorm
Seien V und W Vektorräume und sei [math]f\colon V \rightarrow W[/math] eine lineare Abbildung. Dann ist die Operatornorm definiert als:
[math]\|f\| = \sup_{x \in V\setminus\{0\}} \frac{\|f(x)\|_W}{\|x\|_V} = \sup_{\|x\|_V = 1} \|f(x)\|_W[/math]
Literatur
Otto Forster - Analysis 2 11.Auflage 2017
Quellen
Autoren
Arian Gjini, Alassane Diagne, Robin Klotzbücher