Magische Quadrate: Unterschied zwischen den Versionen

Aus FunFacts Wiki
Zur Navigation springen Zur Suche springen
(Habe den letzten Absatz mit Vorlagen entfernt)
Zeile 1: Zeile 1:
 
==Definition==
 
==Definition==
 
[[Datei:Bild1.png|mini|102x102px]]
 
[[Datei:Bild1.png|mini|102x102px]]
−
Ein magisches Quadrat der Ordnung n beschreibt eine n×n Matrix, in welcher paarweise verschiedene ganze Zahlen, häufig 1,..., <math>n^2 </math>, so angeordnet sind, dass die Summe der Zeilen- und Spalteneinträgen dem gleichen Wert entspricht. Diesen nennt man die magische Summe. Die summierten Einträge der Hauptdiagonalen sind ebenfalls gleich der magischen Summe.
+
Ein '''magisches Quadrat''' der Ordnung n beschreibt eine n×n Matrix, in welcher paarweise verschiedene ganze Zahlen, häufig 1,..., <math>n^2 </math>, so angeordnet sind, dass die Summe der Zeilen- und Spalteneinträge, sowie die summierten Einträge der Hauptdiagonalen, dem gleichen Wert entspricht. Diesen nennt man die '''magischen Summe <math> s^*</math>'''.  
−
Man spricht von einem semimagischen Quadrat, falls die Hauptdiagonalen nicht der magischen Summe entsprechen.
+
Man spricht von einem '''semimagischen''' Quadrat, falls die Hauptdiagonalen nicht der magischen Summe entsprechen.
 
<br />Für die Einträge <math> 1,.., n^2 </math> entspricht die magische Summe <math> s^* = \frac{1}{n} \sum\limits_{k=1}^{n^2} k</math>.
 
<br />Für die Einträge <math> 1,.., n^2 </math> entspricht die magische Summe <math> s^* = \frac{1}{n} \sum\limits_{k=1}^{n^2} k</math>.
−
== Magische Quadrate niedriger Ordnung ==
+
 
−
<!-- Im folgenden betrachten wir magische Quadrate mit niedriger Ordnung. Da sich durch komponentenweise Addition zweier magischer Quadrate und die Multiplikation mit einem Skalar nur die magische Summe ändert, aber die Eigenschaft des magischen Quadrats erhalten bleibt, betrachten wir im folgenden nur ??? magische Quadrate. !-->
+
== besondere magische Quadrate ==
−
=== Magische Quadrate 1-ter Ordnung ===
+
===Pandiagonale magische Quadrate ===
−
Magische Quadrate erster Ordnung besitzen nur einen Eintrag und sind somit trivial, da jede 1×1-Matrix die Eigenschaft eines magischen Quadrates erfüllt.
+
[[Datei:Pandiagonal.png|mini|110x110px]]
 +
Pandiagonale magische oder auch panmagische Quadrate erfüllen die zusätzliche Eigenschaft, dass die Summe der erweiterten Nebendiagonalen ebenfalls der magischen Summe entsprechen. Panmagische Quadrate sind gerader durch vier teilbarer Ordnung oder ungerader durch fünf teilbarer Ordnung. Somit ist ein pandiagonales magisches Quadrat mindestens von Ordnung vier.
 +
==== Beispiel====
 +
<math>
 +
\begin{bmatrix}
 +
25 & 64 & 2 & 39 \\
 +
8 & 33 & 31 & 58 \\
 +
63 & 26 & 40 & 1 \\
 +
34 & 7 & 57 & 32 \\
 +
\end{bmatrix}
 +
</math>
 +
Es gilt <math> s^*= 25+33+40+32 = 130 </math><br/>
 +
<math>8+26+57+39=130 </math>
 +
 
 +
<math> 63+7+2+58=130</math>
 +
 
 +
<math> 64+31+1+34=130</math>
 +
 
 +
<math>8+64+57+1=130 </math>
 +
 
 +
<math>63+33+2+32=130 </math>
 +
 
 +
<math>7+40+58+25=130 </math>
 +
 
 +
===Symmetrische magische Quadrate ===
 +
Man spricht von symmetrisch magischen Quadraten, falls Einträge die um  den Mittelpunkt zueinander punktsymmetrisch sind summiert denselben Wert ergeben. Ist das Quadrat mit den den Werten <math> 1,...,n^2</math> gefüllt, so entspricht diese Summe <math> n^2+1</math>.
 +
==== Beispeil 1====
 +
<math>
 +
\begin{bmatrix}
 +
8 & 3 &4 \\
 +
1 & 5 & 9\\
 +
6 & 7 & 2 \\
 +
\end{bmatrix}
 +
</math>
 +
Es gilt <math>8+2=3+7=4+6=1+9=10 = 3^2+1 </math>
 +
==== Beispiel 2====
 +
<math>
 +
\begin{bmatrix}
 +
16 & 2 &3 & 13 \\
 +
5 & 11 & 10 & 8\\
 +
9 & 7 & 6 & 12 \\
 +
4 & 14 & 15 & 1
 +
\end{bmatrix}
 +
</math>
 +
Es gilt <math>16+1=11+6=13+4=7+10=17 = 4^2+1 </math>
 +
=== Gerahmte magische Quadrate  ===
 +
Ein gerahmtes magisches Quadrat der Ordnung n umschließt ein magisches Quadrate der Ordnung n-2. Das heißt, wenn man die äußeren Spalten und Zeilen entfernt erfüllt das restliche Quadrat noch immer die Eigenschaften eines magischen Quadrats.
 +
==== Beispiel ====
 +
<math>
 +
\begin{bmatrix}
 +
20& 1& 21 & 19&4 \\
 +
2& 14 & 15 &10 &24\\
 +
3& 9 & 13 & 17& 23\\
 +
18& 16 & 11 &12 &8\\
 +
22& 25&5&7&6
 +
\end{bmatrix}
 +
</math>
 +
ist ein magisches Quadrat der Ordnung 5
 +
<math>
 +
\begin{bmatrix}
 +
14 & 15 & 10\\
 +
9& 13 & 17\\
 +
16& 11 &12 \\
 +
\end{bmatrix}
 +
</math>
 +
ist ein magisches Quadrat der Ordnung 3
 +
 
 +
=== Supermagische Quadrate ===
 +
Ein magisches Quadrat mit den Einträgen <math> 1,...,n^2</math> heißt supermagisches Quadrat, falls es folgende Eigenschaften erfüllt
 +
# alle <math> 2 \times 2 -</math>Teilquadrate haben dieselbe Summe <math> s_{2 \times 2}=2(n^2+1)</math>
 +
# das Quadrat hat die Ordnung <math> n=4k </math> mit <math> k \in \mathbb{N} </math>
 +
# summiert man zwei Elemente einer Diagonale, die den Abstand n/2 haben so ist dieser Wert stets gleich <math>d=n^2+1 </math>
 +
==== Beispiel ====
 +
<math>
 +
\begin{bmatrix}
 +
1&15&10&8\\
 +
12&6&3&13\\
 +
7&9&16&2\\
 +
14&4&5&11
 +
\end{bmatrix}
 +
</math>
 +
#<math>1+15+12+6=10+8+3+13=...=9+16+4+5=6+3+9+16=2(4^2+1)=34</math>
 +
#das Quadrat hat die Ordnung 4
 +
#<math>1+16=8+9=...=15+2=7+10=4^2+1=17</math>
 +
 
 +
== magische Quadrate niedriger Ordnung ==
 +
<!-- Im folgenden betrachten wir magische Quadrate mit niedriger Ordnung. Da durch komponentenweise Addition zweier magischer Quadrate und der Multiplikation mit einem Skalar sich nur die magische Summer ändert, aber die Eigenschaft des magischen Quadrats erhalten bleibt betrachten wir im folgenden nur ??? magische Quadrate. !-->
 +
=== magische Quadrate 1-ter Ordnung ===
 +
Magische Quadrate erster Ordnung besitzen nur einen Eintrag und sind somit trivial, da jeden 1×1-Matrix die Eigenschaft eines magischen Quadrates erfüllt.
  
 
magisches Quadrat 1-ter Ordnung
 
magisches Quadrat 1-ter Ordnung
Zeile 16: Zeile 104:
 
</math>
 
</math>
 
mit <math>a \in \mathbb{Z} </math>
 
mit <math>a \in \mathbb{Z} </math>
−
=== Magische Quadrate 2-ter Ordnung ===
+
=== magische Quadrate 2-ter Ordnung ===
−
Nach der oben aufgeführten Definition von magischen ??? existieren keine magischen Quadrate zweiter Ordnung. Vernachlässigt man die Bedingung der paarweise verschiedenen Einträge, haben magische bzw. semimagische Quadrate folgende Form:
+
Nach der oben aufgeführten Definition von magischen existieren keine magischen Quadrate zweiter Ordnung. Vernachlässigt man die Bedingung der paarweise verschiedenen Einträge haben magische bzw. semimagische Quadrate folgende Form
  
 
magisches Quadrat 2-ter Ordnung
 
magisches Quadrat 2-ter Ordnung
Zeile 36: Zeile 124:
 
</math>  
 
</math>  
 
mit <math>a, b \in \mathbb{Z} </math>
 
mit <math>a, b \in \mathbb{Z} </math>
−
=== Magische Quadrate 3-ter Ordnung ===
+
=== magische Quadrate 3-ter Ordnung ===
−
Um den Aufbau eines magischen Quadrats dritter Ordnung zu verdeutlichen betrachten wir folgende Matrix
+
Um den Aufbau eines magisches Quadrats dritter Ordnung zu verdeutlichen betrachten wir folgende Matrix
  
 
A=
 
A=
Zeile 49: Zeile 137:
 
mit <math>a, b,...,i \in \mathbb{Z} </math>
 
mit <math>a, b,...,i \in \mathbb{Z} </math>
  
−
Sei <math>s^* \in \mathbb{Z}</math> die magische Summe, so muss A folgende Eigenschaft erfüllen:
+
Sei <math>s^* \in \mathbb{Z}</math> die magische Summe so muss A folgende Eigenschaft erfüllen:
  
 
<math>s^*  - e = a + i = b + h = c + g = f + d </math> < br/>
 
<math>s^*  - e = a + i = b + h = c + g = f + d </math> < br/>
−
Daraus lässt sich folgern, dass <math>a + b + ... + h + i = 4* (s^*-e)+e </math> gilt. Darüber hinaus gilt <math> a+b+...+h+i= 3s^*</math>, daraus folgt <math> s^* = 3e</math>.
+
Daraus lässt sich folgern, dass <math>a + b + ... + h + i = 4* (s^*-e)+e </math> gilt. Darüber hinaus gilt <math> a+b+...+h+i= 3s^*</math> daraus folgt <math> s^* = 3e</math>
  
−
Mit diesen zusätzlichen Voraussetzungen lassen sich magische Quadrate der Ordnung 3 für die Zahlen 1,...,9 leicht konstruieren. Die magische Summe ergibt sich aus <math> s^* = \frac{1}{3} \sum\limits_{k=1}^{9} k = 15</math>. Somit gilt <math>r=5 </math> und <math> 10 = a + i = b + h = c + g = f + d</math>. Es gilt <math> 10 = 1+9 = 2+8 = 3 + 7= 4+6</math>. Nehmen wir nun a=1 an, so erhalten wir
+
Mit diesen zusätzlichen Vorraussetzungen lassen sich magische Quadrate der Ordnung 3 für die Zahlen 1,...,9 leicht konstruieren. Die magische Summe ergibt sich aus <math> s^* = \frac{1}{3} \sum\limits_{k=1}^{9} k = 15</math> somit gilt <math>r=5 </math> und <math> 10 = a + i = b + h = c + g = f + d</math>. Es gilt <math> 10 = 1+9 = 2+8 = 3 + 7= 4+6</math>. Nehmen wir nun a=1 an, so erhalten wir
−
<math>14 = b+c = d+g </math> und <math> 6 = f+c =h+g</math>. Da es je nur ein Paar gibt, welches gleich 14 bzw. gleich 5 ist, folgt, dass die Werte 1 und 9 nicht in einer der Ecken liegen können. Des Weiteren ist 1 stets von 6 und 8 umgeben und 9 stets von 2 und 4. Daraus ergeben sich folgende mögliche magischen Quadrate:
+
<math>14 = b+c = d+g </math> und <math> 6 = f+c =h+g</math>. Da es je nur ein Paar gibt, welches gleich 14 bzw. gleich 5 ist folgt, dass die Werte 1 und 9 nicht in einer der Ecken liegen können. Des Weiteren ist 1 stets von 6 und 8 umgeben und 9 stets von 2 und 4. Daraus ergeben sich folgende mögliche magische Quadrate:
  
 
<math>
 
<math>
Zeile 122: Zeile 210:
  
 
Hierbei handelt es sich genau genommen nur um ein magisches Quadrat, welches lediglich gespiegelt und/oder rotiert wird.
 
Hierbei handelt es sich genau genommen nur um ein magisches Quadrat, welches lediglich gespiegelt und/oder rotiert wird.
−
== Besondere magische Quadrate ==
 
−
===Pandiagonale magische Quadrate ===
 
−
[[Datei:Pandiagonal.png|mini|110x110px]]
 
−
Pandiagonale magische oder auch panmagische Quadrate erfüllen die zusätzliche Eigenschaft, dass die Summe der erweiterten Nebendiagonalen ebenfalls der magischen Summe entsprechen. Panmagische Quadrate sind gerader durch vier teilbarer Ordnung oder ungerader durch fünf teilbarer Ordnung. Somit ist ein pandiagonales magisches Quadrat mindestens von Ordnung vier.
 
−
==== Beispiel====
 
−
<math>
 
−
\begin{bmatrix}
 
−
25 & 64 & 2 & 39 \\
 
−
8 & 33 & 31 & 58 \\
 
−
63 & 26 & 40 & 1 \\
 
−
34 & 7 & 57 & 32 \\
 
−
\end{bmatrix}
 
−
</math>
 
−
 
−
Es gilt <math> s^*= 25+33+40+32 = 130 </math><br />
 
−
<math>8+26+57+39=130 </math>
 
−
 
−
<math> 63+7+2+58=130</math>
 
−
 
−
<math> 64+31+1+34=130</math>
 
−
 
−
<math>8+64+57+1=130 </math>
 
−
 
−
<math>63+33+2+32=130 </math>
 
−
 
−
<math>7+40+58+25=130 </math>
 
−
 
−
===Symmetrische magische Quadrate ===
 
−
Man spricht von symmetrisch magischen Quadraten, falls Einträge, die um  den Mittelpunkt zueinander punktsymmetrisch sind, summiert denselben Wert ergeben. Ist das Quadrat mit den Werten <math> 1,...,n^2</math> gefüllt, so entspricht diese Summe <math> n^2+1</math>.
 
−
==== Beispiel 1====
 
−
<math>
 
−
\begin{bmatrix}
 
−
8 & 3 &4 \\
 
−
1 & 5 & 9\\
 
−
6 & 7 & 2 \\
 
−
\end{bmatrix}
 
−
</math>
 
−
Es gilt <math>8+2=3+7=4+6=1+9=10 = 3^2+1 </math>
 
−
==== Beispiel 2====
 
−
<math>
 
−
\begin{bmatrix}
 
−
16 & 2 &3 & 13 \\
 
−
5 & 11 & 10 & 8\\
 
−
9 & 7 & 6 & 12 \\
 
−
4 & 14 & 15 & 1
 
−
\end{bmatrix}
 
−
</math>
 
−
Es gilt <math>16+1=11+6=13+4=7+10=17 = 4^2+1 </math>
 
−
=== Gerahmte magische Quadrate  ===
 
−
Ein gerahmtes magisches Quadrat der Ordnung n umschließt ein magisches Quadrat der Ordnung n-2. Das heißt, wenn man die äußeren Spalten und Zeilen entfernt, erfüllt das restliche Quadrat noch immer die Eigenschaften eines magischen Quadrats.
 
−
==== Beispiel ====
 
−
<math>
 
−
\begin{bmatrix}
 
−
20& 1& 21 & 19&4 \\
 
−
2& 14 & 15 &10 &24\\
 
−
3& 9 & 13 & 17& 23\\
 
−
18& 16 & 11 &12 &8\\
 
−
22& 25&5&7&6
 
−
\end{bmatrix}
 
−
</math>
 
−
ist ein magisches Quadrat der Ordnung 5.
 
−
<math>
 
−
\begin{bmatrix}
 
−
14 & 15 & 10\\
 
−
9& 13 & 17\\
 
−
16& 11 &12 \\
 
−
\end{bmatrix}
 
−
</math>
 
−
ist ein magisches Quadrat der Ordnung 3.
 
−
 
−
=== Supermagische Quadrate ===
 
−
Ein magisches Quadrat mit den Einträgen <math> 1,...,n^2</math> heißt supermagisches Quadrat, falls es folgende Eigenschaften erfüllt:
 
−
# alle <math> 2 \times 2 -</math>Teilquadrate haben dieselbe Summe <math> s_{2 \times 2}=2(n^2+1)</math>
 
−
# das Quadrat hat die Ordnung <math> n=4k </math> mit <math> k \in \mathbb{N} </math>
 
−
# summiert man zwei Elemente einer Diagonale, die den Abstand n/2 haben so ist dieser Wert stets gleich <math>d=n^2+1 </math>
 
−
==== Beispiel ====
 
−
<math>
 
−
\begin{bmatrix}
 
−
1&15&10&8\\
 
−
12&6&3&13\\
 
−
7&9&16&2\\
 
−
14&4&5&11
 
−
\end{bmatrix}
 
−
</math>
 
−
#<math>1+15+12+6=10+8+3+13=...=9+16+4+5=6+3+9+16=2(4^2+1)=34</math>
 
−
#das Quadrat hat die Ordnung 4
 
−
#<math>1+16=8+9=...=15+2=7+10=4^2+1=17</math>
 
−
 
−
==Gruppeneigenschaften bei symmetrischen magischen 4x4-Quadraten==
 
−
Wir betrachten zunächst folgendes magisches 4x4-Quadrat, welches unsere Grundform <math>G</math> darstellen wird:
 
−
<gallery widths="200" heights="100">
 
−
Datei:Gruppemagischequadrate1.jpg
 
−
</gallery>
 
−
Durch Vertauschungen von Einträgen aus unserem magischen Quadrat <math>G</math>, erhalten wir diese weiteren magischen Quadrate:
 
−
 
−
1. Das magische Quadrat <math>A</math>.
 
−
<gallery widths="200" heights="100">
 
−
Datei:Gruppemagischequadrate2.jpg
 
−
Datei:Gruppemagischequadrate4.jpg
 
−
</gallery>
 
−
 
−
2. Das magische Quadrat <math>B</math>.
 
−
<gallery widths="200" heights="100">
 
−
Datei:Gruppemagischequadrate3.jpg
 
−
Datei:Gruppemagischequadrate5.jpg
 
−
</gallery>
 
−
 
−
3. Das magische Quadrat <math>C</math>.
 
−
<gallery widths="200" heights="100">
 
−
Datei:Gruppemagischequadrate6.jpg
 
−
Datei:Gruppemagischequadrate7.jpg
 
−
</gallery>
 
−
 
−
Nun muss noch eine Verknüpfung definiert werden. Verknüpfen wir <math>A</math> mit <math>B</math>, so führen wir genau die Vertauschungen auf unsere Grundform <math>G</math> aus, die verwendet wurden, um <math>A</math> beziehungsweise <math>B</math> aus der Grundform <math>G</math> zu erhalten. Das heißt, wir vertauschen jeweils die grünen und die blauen Einträge in der entsprechenden Zeile. Es ergibt sich (wie man durch leichtes Nachrechnen herausfinden kann) das folgende magische Quadrat <math>A \circ B </math>.
 
−
<gallery widths="200" heights="100">
 
−
Datei:Gruppemagischequadrate8.jpg
 
−
Datei:Gruppemagischequadrate12.jpg
 
−
</gallery>
 
−
 
−
Analog funktionieren die Verknüpfungen  <math>A \circ C </math> und <math>B \circ C </math>.
 
−
Für <math>A \circ C </math> führen wir also folgende Vertauschungen durch:
 
−
<gallery widths="200" heights="100">
 
−
Datei:Gruppemagischequadrat9.jpg
 
−
Datei:Gruppemagischequadrate13.jpg
 
−
</gallery>
 
−
 
−
<math>B \circ C </math> erhalten wir dementsprechend durch folgendes Vorgehen:
 
−
<gallery widths="200" heights="100">
 
−
Datei:Gruppemagischequadrate10.jpg
 
−
Datei:Gruppemagischequadrate14.jpg
 
−
</gallery>
 
−
 
−
Da wir für <math>A \circ B </math> die gleichen Vertauschungen auf unsere Grundform <math>G </math> anwenden, wie für <math>B \circ A </math>, gilt <math>A \circ B = B \circ A </math>. Analog folgt <math>A \circ C =  C \circ A </math> und <math>B \circ C = C \circ B </math>.
 
−
 
−
Wollen wir <math>A \circ B \circ C </math> erhalten, so müssen wir alle Vertauschungen durchführen. Es ergibt sich also:
 
−
<gallery widths="200" heights="100">
 
−
Datei:Gruppemagischequadrate11.jpg
 
−
Datei:Gruppemagischequadrate15.jpg
 
−
</gallery>
 
−
Nun können wir also folgende Verknüpfungstabelle betrachten und feststellen, dass die Menge <math>M = \{G, A, B, C, A \circ B, A \circ C, B \circ C, A \circ B \circ C \} </math> eine Gruppe darstellt.
 
−
 
−
{| class="wikitable"
 
−
|+ Verknüfungstabelle
 
−
|-
 
−
! <math>\circ </math> !! <math>G </math>!! <math>A </math> !! <math>B </math> !! <math>C </math> !! <math>A \circ B </math> !! <math>A \circ C </math> !! <math>B \circ C </math> !! <math>A \circ B \circ C </math>
 
−
|-
 
−
| <math>G </math> || <math>G </math> || <math>A </math> || <math>B </math> || <math>C </math> || <math>A \circ B </math> || <math>A \circ C </math>|| <math>B \circ C </math>|| <math>A \circ B \circ C </math>
 
−
|-
 
−
| <math>A </math> || <math>A </math> || <math>G </math> || <math>A \circ B </math>|| <math>A \circ C </math> || <math>B </math> || <math>C </math> || <math>A \circ B \circ C </math> || <math>B \circ C </math>
 
−
|-
 
−
| <math>B </math> || <math>B </math> || <math>A \circ B </math> || <math>G </math> || <math>B \circ C </math> || <math>A </math> || <math>A \circ B \circ C </math> || <math>C </math> || <math>A \circ C </math>
 
−
|-
 
−
| <math>C </math> || <math>C </math> || <math>A \circ C </math> || <math>B \circ C </math> || <math>G </math> || <math>A \circ B \circ C </math> || <math>A </math> || <math>B </math> || <math>A \circ B </math>
 
−
|-
 
−
| <math>A \circ B </math> || <math>A \circ B </math> || <math>B </math> || <math>A </math> || <math>A \circ B \circ C </math> || <math>G </math>|| <math>B \circ C </math> || <math>A \circ C </math> || <math>C </math>
 
−
|-
 
−
| <math>A \circ C </math> || <math>A \circ C </math> || <math>C </math> || <math>A \circ B \circ C </math> || <math>A </math> || <math>B \circ C </math> || <math>G </math> || <math>A \circ B </math> || <math>B </math>
 
−
|-
 
−
| <math>B \circ C </math> || <math>B \circ C </math> || <math>A \circ B \circ C </math> || <math>C </math> || <math>B </math> || <math>A \circ C </math> || <math>A \circ B </math> || <math>G </math> || <math>A </math>
 
−
|-
 
−
| <math>A \circ B \circ C </math> || <math>A \circ B \circ C </math> || <math>B \circ C </math> || <math>A \circ C </math> || <math>A \circ B </math> || <math>C </math> || <math>B </math> || <math>A </math> || <math>G </math>
 
−
|}
 
−
 
−
Die Menge <math>M</math> bildet also eine Gruppe, wobei unsere Grundform <math>G</math> das neutrale Element darstellt und die Elemente selbstinvers sind, da zweifaches Vertauschen wieder die Grundform <math>G</math> ergibt. Assoziativität ist offensichtlich gegeben, da die Reihenfolge der Vertauschungen keine Rolle spielt.
 
−
 
−
Auch bei pandiagonalen magischen Quadraten können Gruppeneigenschaften beobachtet werden. Mehr dazu findet sich [https://www.michael-holzapfel.de/themen/mag_quadrat/mq-4/mq4.htm hier].
 
−
 
−
== Geschichte ==
 
−
Es ist nicht bekannt, wann genau Wissenschaftler*innen begannen, sich mit magischen Quadraten zu beschäftigen, jedoch existieren bereits fortgeschrittene griechische Bücher über die Konstruktion magischer Quadrate aus dem 9. Jahrhundert. Im Arabischen Raum wurden im 11. und 12. Jahrhundert weitere Konstruktionsmöglichkeiten für gewöhnliche und auch pandiagonale magische Quadrate entdeckt. Erst im späten Mittelalter wurden arabische Texte über magische Quadrate in Europa auf Latein übersetzt, daraufhin wurden diese auch dort studiert. Auch in China und Indien können magische Quadrate gefunden werden. Eine Legende besagt, dass in China bereits vor dem ersten Jahrhundert vor Christus das erste magische Quadrat auf dem Rücken einer Schildkröte entdeckt wurde. Diese waren jedoch ausschließlich dritter Ordnung und erst im 13. Jahrhundert wurden dort magische Quadrate höherer Ordnung studiert, was sich auf arabische Texte zurückführen lässt.
 
−
 
−
== Konstruktion ==
 
−
Eine in Europa im 17. Jahrhundert durch Simon de la Loubère bekannt gewordene Konstruktionsmöglichkeit für magische Quadrate ungerader Ordnung, die dieser auf seiner Reise nach Thailand von einem anderen Reisenden lernte, ist die folgende:
 
−
* Zunächst setzt man eine 1 in das mittlere Feld der oberen Reihe
 
−
* Nachdem man eine Zahl in ein Feld der oberen Reihe geschrieben hat, schreibt man die nächste in das unterste Feld der nächsten Spalte
 
−
* Wenn man eine Zahl in das letzte Feld einer Reihe geschrieben hat, so schreibt man die nächste in das erste Feld der Reihe darüber
 
−
* In allen anderen Fällen schreibt man die nächste Zahl in das Feld rechts über der zuvor geschriebenen Zahl
 
−
* Falls ein Feld bereits besetzt ist, so schreibt man die nächste Zahl in das Feld unter der zuvor geschriebenen Zahl
 
−
<gallery perrow="9" caption="Beispiel eines magischen Quadrats der Größe 3x3">
 
−
Datei:Screenshot 20210910-115309 Noteshelf.jpg
 
−
Datei:Screenshot 20210910-115326 Noteshelf.jpg
 
−
Datei:Screenshot 20210910-115400 Noteshelf.jpg
 
−
Datei:Screenshot 20210910-115422 Noteshelf.jpg
 
−
Datei:Screenshot 20210910-115445 Noteshelf.jpg
 
−
Datei:Screenshot 20210910-115505 Noteshelf.jpg
 
−
Datei:Screenshot 20210910-115520 Noteshelf.jpg
 
−
Datei:Screenshot 20210910-115538 Noteshelf.jpg
 
−
Datei:Screenshot 20210910-115557 Noteshelf.jpg
 
−
</gallery>
 
  
 
== Weblinks ==
 
== Weblinks ==
 
https://www.magic-squares.info/
 
https://www.magic-squares.info/
−
 
−
https://www.michael-holzapfel.de/themen/mag_quadrat/mq-4/mq4.htm
 
 
== Einzelnachweise/Literaturverzeichnis ==
 
== Einzelnachweise/Literaturverzeichnis ==
 
Beck, Matthias; Robins, Sinai: Das Kontinuum diskret berechnen. Kapitel 6. <br />
 
Beck, Matthias; Robins, Sinai: Das Kontinuum diskret berechnen. Kapitel 6. <br />
Zeile 323: Zeile 221:
 
Joanna Schnorr<br />
 
Joanna Schnorr<br />
 
Julia Bohn
 
Julia Bohn
 +
 +
== Vorlage ==
 +
===Überschrift 1 ===
 +
==== Überschrift 2====
 +
Hier kann man ganz normal schreiben :)
 +
 +
<math> \text{hier müsste es wie in der Latex equation-Funktion Formeln schreiben können } x \in \mathbb{N} : x \in \mathbb{R} </math>
 +
#nummerierte Aufzählungen
 +
## neue Ebene
 +
###usw.
 +
* Aufzählung mit Punkt
 +
** tiefere Ebene
 +
*::- Was passiert hier
 +
; Aufzählung ohne Zeichen
 +
:Unterpunkt
 +
; Aufzählung 2 ohne Zeichen
 +
<q> Hier wird etwas wichtiges zitiert </q>
 +
<blockquote>
 +
hier könnte Ihr eingerückter Text stehen
 +
</blockquote>
 +
<u> unterstrichen </u> <s> durchgestrichen </s>
 +
 +
Durch diesen Befehl kann <br />innerhalb eines Absatz ein Zeilenumsprung erzeugt werden
 +
<!-- HIER PLATZ FÜR MEHR --!>-->

Version vom 24. September 2021, 07:02 Uhr

Definition

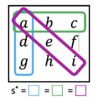
Bild1.png

Ein magisches Quadrat der Ordnung n beschreibt eine n×n Matrix, in welcher paarweise verschiedene ganze Zahlen, häufig 1,..., [math]n^2 [/math], so angeordnet sind, dass die Summe der Zeilen- und Spalteneinträge, sowie die summierten Einträge der Hauptdiagonalen, dem gleichen Wert entspricht. Diesen nennt man die magischen Summe [math] s^*[/math]. Man spricht von einem semimagischen Quadrat, falls die Hauptdiagonalen nicht der magischen Summe entsprechen.
Für die Einträge [math] 1,.., n^2 [/math] entspricht die magische Summe [math] s^* = \frac{1}{n} \sum\limits_{k=1}^{n^2} k[/math].

besondere magische Quadrate

Pandiagonale magische Quadrate

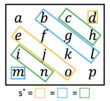
Pandiagonal.png

Pandiagonale magische oder auch panmagische Quadrate erfüllen die zusätzliche Eigenschaft, dass die Summe der erweiterten Nebendiagonalen ebenfalls der magischen Summe entsprechen. Panmagische Quadrate sind gerader durch vier teilbarer Ordnung oder ungerader durch fünf teilbarer Ordnung. Somit ist ein pandiagonales magisches Quadrat mindestens von Ordnung vier.

Beispiel

[math] \begin{bmatrix} 25 & 64 & 2 & 39 \\ 8 & 33 & 31 & 58 \\ 63 & 26 & 40 & 1 \\ 34 & 7 & 57 & 32 \\ \end{bmatrix} [/math] Es gilt [math] s^*= 25+33+40+32 = 130 [/math]
[math]8+26+57+39=130 [/math]

[math] 63+7+2+58=130[/math]

[math] 64+31+1+34=130[/math]

[math]8+64+57+1=130 [/math]

[math]63+33+2+32=130 [/math]

[math]7+40+58+25=130 [/math]

Symmetrische magische Quadrate

Man spricht von symmetrisch magischen Quadraten, falls Einträge die um den Mittelpunkt zueinander punktsymmetrisch sind summiert denselben Wert ergeben. Ist das Quadrat mit den den Werten [math] 1,...,n^2[/math] gefüllt, so entspricht diese Summe [math] n^2+1[/math].

Beispeil 1

[math] \begin{bmatrix} 8 & 3 &4 \\ 1 & 5 & 9\\ 6 & 7 & 2 \\ \end{bmatrix} [/math] Es gilt [math]8+2=3+7=4+6=1+9=10 = 3^2+1 [/math]

Beispiel 2

[math] \begin{bmatrix} 16 & 2 &3 & 13 \\ 5 & 11 & 10 & 8\\ 9 & 7 & 6 & 12 \\ 4 & 14 & 15 & 1 \end{bmatrix} [/math] Es gilt [math]16+1=11+6=13+4=7+10=17 = 4^2+1 [/math]

Gerahmte magische Quadrate

Ein gerahmtes magisches Quadrat der Ordnung n umschließt ein magisches Quadrate der Ordnung n-2. Das heißt, wenn man die äußeren Spalten und Zeilen entfernt erfüllt das restliche Quadrat noch immer die Eigenschaften eines magischen Quadrats.

Beispiel

[math] \begin{bmatrix} 20& 1& 21 & 19&4 \\ 2& 14 & 15 &10 &24\\ 3& 9 & 13 & 17& 23\\ 18& 16 & 11 &12 &8\\ 22& 25&5&7&6 \end{bmatrix} [/math] ist ein magisches Quadrat der Ordnung 5 [math] \begin{bmatrix} 14 & 15 & 10\\ 9& 13 & 17\\ 16& 11 &12 \\ \end{bmatrix} [/math] ist ein magisches Quadrat der Ordnung 3

Supermagische Quadrate

Ein magisches Quadrat mit den Einträgen [math] 1,...,n^2[/math] heißt supermagisches Quadrat, falls es folgende Eigenschaften erfüllt

  1. alle [math] 2 \times 2 -[/math]Teilquadrate haben dieselbe Summe [math] s_{2 \times 2}=2(n^2+1)[/math]
  2. das Quadrat hat die Ordnung [math] n=4k [/math] mit [math] k \in \mathbb{N} [/math]
  3. summiert man zwei Elemente einer Diagonale, die den Abstand n/2 haben so ist dieser Wert stets gleich [math]d=n^2+1 [/math]

Beispiel

[math] \begin{bmatrix} 1&15&10&8\\ 12&6&3&13\\ 7&9&16&2\\ 14&4&5&11 \end{bmatrix} [/math]

  1. [math]1+15+12+6=10+8+3+13=...=9+16+4+5=6+3+9+16=2(4^2+1)=34[/math]
  2. das Quadrat hat die Ordnung 4
  3. [math]1+16=8+9=...=15+2=7+10=4^2+1=17[/math]

magische Quadrate niedriger Ordnung

magische Quadrate 1-ter Ordnung

Magische Quadrate erster Ordnung besitzen nur einen Eintrag und sind somit trivial, da jeden 1×1-Matrix die Eigenschaft eines magischen Quadrates erfüllt.

magisches Quadrat 1-ter Ordnung [math] \begin{bmatrix} a \end{bmatrix} [/math] mit [math]a \in \mathbb{Z} [/math]

magische Quadrate 2-ter Ordnung

Nach der oben aufgeführten Definition von magischen existieren keine magischen Quadrate zweiter Ordnung. Vernachlässigt man die Bedingung der paarweise verschiedenen Einträge haben magische bzw. semimagische Quadrate folgende Form

magisches Quadrat 2-ter Ordnung [math] \begin{bmatrix} a & a \\ a & a \\ \end{bmatrix} [/math] mit [math]a \in \mathbb{Z} [/math]

semimagisches Quadrat 2-ter Ordnung [math] \begin{bmatrix} a & b \\ b & a\\ \end{bmatrix} [/math] mit [math]a, b \in \mathbb{Z} [/math]

magische Quadrate 3-ter Ordnung

Um den Aufbau eines magisches Quadrats dritter Ordnung zu verdeutlichen betrachten wir folgende Matrix

A= [math] \begin{bmatrix} a & b &c \\ d & e & f\\ g & h & i \\ \end{bmatrix} [/math] mit [math]a, b,...,i \in \mathbb{Z} [/math]

Sei [math]s^* \in \mathbb{Z}[/math] die magische Summe so muss A folgende Eigenschaft erfüllen:

[math]s^* - e = a + i = b + h = c + g = f + d [/math] < br/> Daraus lässt sich folgern, dass [math]a + b + ... + h + i = 4* (s^*-e)+e [/math] gilt. Darüber hinaus gilt [math] a+b+...+h+i= 3s^*[/math] daraus folgt [math] s^* = 3e[/math]

Mit diesen zusätzlichen Vorraussetzungen lassen sich magische Quadrate der Ordnung 3 für die Zahlen 1,...,9 leicht konstruieren. Die magische Summe ergibt sich aus [math] s^* = \frac{1}{3} \sum\limits_{k=1}^{9} k = 15[/math] somit gilt [math]r=5 [/math] und [math] 10 = a + i = b + h = c + g = f + d[/math]. Es gilt [math] 10 = 1+9 = 2+8 = 3 + 7= 4+6[/math]. Nehmen wir nun a=1 an, so erhalten wir [math]14 = b+c = d+g [/math] und [math] 6 = f+c =h+g[/math]. Da es je nur ein Paar gibt, welches gleich 14 bzw. gleich 5 ist folgt, dass die Werte 1 und 9 nicht in einer der Ecken liegen können. Des Weiteren ist 1 stets von 6 und 8 umgeben und 9 stets von 2 und 4. Daraus ergeben sich folgende mögliche magische Quadrate:

[math] \begin{bmatrix} 6 & 1 &8 \\ 7 & 5 & 3\\ 2 & 9 & 4 \\ \end{bmatrix} [/math] beziehungsweise durch Spiegelung [math] \begin{bmatrix} 8 & 1 &6 \\ 3 & 5 & 7\\ 4 & 9 & 2 \\ \end{bmatrix} [/math]

[math] \begin{bmatrix} 2 & 7 &6 \\ 9 & 5 & 1\\ 4 & 3 & 8 \\ \end{bmatrix} [/math] beziehungsweise durch Spiegelung [math] \begin{bmatrix} 4 & 3 &8 \\ 9 & 5 & 1\\ 2 & 7 & 6 \\ \end{bmatrix} [/math]

[math] \begin{bmatrix} 2 & 9 &4 \\ 7 & 5 & 3\\ 6 & 1 & 8 \\ \end{bmatrix} [/math] beziehungsweise durch Spiegelung [math] \begin{bmatrix} 4 & 9 &2 \\ 3 & 5 & 7\\ 8 & 1 & 6 \\ \end{bmatrix} [/math]

[math] \begin{bmatrix} 6 & 7 &2 \\ 1 & 5 & 9\\ 8 & 3 & 4 \\ \end{bmatrix} [/math] beziehungsweise durch Spiegelung [math] \begin{bmatrix} 8 & 3 &4 \\ 1 & 5 & 9\\ 6 & 7 & 2 \\ \end{bmatrix} [/math]

Hierbei handelt es sich genau genommen nur um ein magisches Quadrat, welches lediglich gespiegelt und/oder rotiert wird.

Weblinks

https://www.magic-squares.info/

Einzelnachweise/Literaturverzeichnis

Beck, Matthias; Robins, Sinai: Das Kontinuum diskret berechnen. Kapitel 6.
Sesiano, Jacques: Magic Squares-Their History and Construction from Ancient Times to AD 1600.

AutorInnen

Julia Renner
Joanna Schnorr
Julia Bohn

Vorlage

Überschrift 1

Überschrift 2

Hier kann man ganz normal schreiben :)

[math] \text{hier müsste es wie in der Latex equation-Funktion Formeln schreiben können } x \in \mathbb{N} : x \in \mathbb{R} [/math]

  1. nummerierte Aufzählungen
    1. neue Ebene
      1. usw.
  • Aufzählung mit Punkt
    • tiefere Ebene
    - Was passiert hier
Aufzählung ohne Zeichen
Unterpunkt
Aufzählung 2 ohne Zeichen

Hier wird etwas wichtiges zitiert

hier könnte Ihr eingerückter Text stehen

unterstrichen durchgestrichen

Durch diesen Befehl kann
innerhalb eines Absatz ein Zeilenumsprung erzeugt werden

Abgerufen von „https://funfacts.mathi.uni-heidelberg.de/index.php?title=Magische_Quadrate&oldid=5450“