Goldener Schnitt

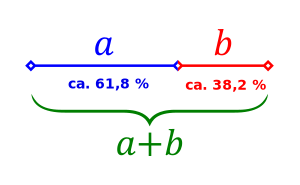
Der "Goldene Schnitt" bezeichnet allgemein ein spezielles Teilungsverhältnis einer Strecke.

Die Besonderheit dieses Verhältnisses besteht darin, die Gesamtstrecke in zwei Teile aufzuteilen, wobei die Gesamtstrecke dasselbe Teilungsverhältnis zur größeren Teilstrecke aufweist, wie auch die größere Teilstrecke zur kleineren Teilstrecke.

Proportionen des Goldenen Schnitts

Den Quotient der Strecken nennt man die Goldene Zahl [math]\Phi[/math].

Herleitung des Goldenen Schnitts

Die Definition lässt sich algebraisch ausdrücken und wie folgt eindeutig lösen:

[math] \Phi = \frac{a}{b} = \frac{a+b}{a} = 1+\frac{b}{a} = 1 + \frac{1}{\Phi}\\\\ [/math]

[math]   \Leftrightarrow  \Phi^{2}   =   \Phi + 1 \\\\ [/math]

[math]   \Leftrightarrow  0 = \Phi^{2} - \Phi - 1 \\\\ [/math]

[math] \Rightarrow \Phi_{1}  =  \frac{1+\sqrt[]{5}}{2}  \approx  1,618\\ [/math]

[math] \Rightarrow \Phi_{2} = \frac{1-\sqrt[]{5}}{2} \approx 0,618 = \frac{1}{\Phi_{1}} [/math]

Wir nennen [math] \Phi_{1} [/math] die Goldene Zahl [math] \Phi [/math] mit den Kehrwert [math] \frac{1}{\Phi}= \Phi - 1 [/math]

[math]\Phi[/math] als "irrationalste" Zahl

Natürlich gibt es keine irrationale Zahl die "irrationaler" als eine andere irrationale Zahl ist. [math]\Phi[/math] lässt sich, wie wir im folgenden sehen werden nur sehr "langsam" durch rationale Zahlen annähern, daher die meist scherzhafte Aussage [math]\Phi[/math] sei die "irrationalste" Zahl.

Kettenbruchdarstellung

Um die Annäherung durch rationale Zahlen vorzunehmen, stellt man die Zahl als unendlichen Kettenbruch dar und bricht diesen an einer Stelle ab. Je später, desto genauer die Annäherung. (mehr )

[math]   \Phi = 1 + \frac{1}{\Phi} = 1 + \frac{1}{1 + \frac{1}{\Phi}} = 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{\Phi}}} = 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{\Phi}}}} \quad ... [/math]

Wir sehen nun, dass der Kettenbruch von [math]\Phi[/math] nur Einsen als Elemente enthält, woraus sich wiederum folgern lässt, dass der Nenner der Näherung durch rationale Zahlen so langsam wie nur möglich wächst und sich somit eine möglichst genaue Approximation nur schlecht durchzuführen ist.

Daher, %wie bereits erwähnt%, die Aussage [math]\Phi[/math] sei die irrationalste nur mögliche Zahl.

Sehr interessant ist hierbei, dass der Näherungsbruch immer aus zwei aufeinanderfolgenden Fibonacci-Zahlen besteht!

Annäherung durch Kettenbruchverfahren

Abbruch nach n Elementen	1	2	3	4	5	6	7	8	[math]\vdots[/math]	Die rekursive Bildungsformel lautet: [math] \frac{p_{n}}{q_{n}} = \frac{p_{n-1} + q_{n-1}}{p_{n-1}} [/math] mit [math] p_{0},q_{0} = 1 [/math]
Näherungswert	2	[math] \frac{3}{2} [/math]	[math] \frac{5}{3} [/math]	[math] \frac{8}{5} [/math]	[math] \frac{13}{8} [/math]	[math] \frac{21}{13} [/math]	[math] \frac{34}{21} [/math]	[math] \frac{55}{34} [/math]
Abweichung von [math] \Phi [/math] in %	23,6	7,3	3	1,1	0,43	0,16	0,062	0,024

Kettenwurzeldarstellung

Alternativ lässt sich [math]\Phi[/math] auch durch eine unendliche Kettenwurzel nähern, dies folgt aus [math]\Phi^{2} = \Phi + 1[/math]

[math] \Phi = \sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+...}}}} [/math]

%Geometrische Konstruktion von [math]\Phi[/math]

Unterscheidung in äußere und innere Teilung

Innere Teilung

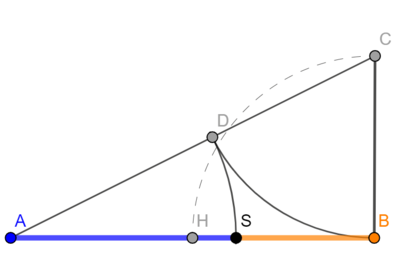
"klassische Methode" Gegeben sei eine beliebige Länge [math] \overline{AB}[/math]. Die Strecke [math] \overline{BC}[/math] steht senkrecht zu [math] \overline{AB}[/math] im Punkt B und hat die Länge [math] \frac{\overline{AB}}{2}[/math]. Der Kreis um C mit Radius [math] \overline{BC}[/math] schneidet die Strecke [math] \overline{AC}[/math] im Punkt D. Der Kreis um A mit Radius [math] \overline{AD}[/math] teilt die Strecke [math] \overline{AB}[/math] im Verhältnis des Goldenen Schnitts.

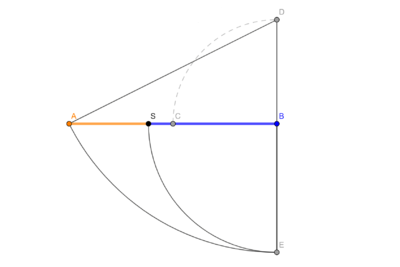
Methode nach Euklid Gegeben sei eine beliebige Länge [math] \overline{AB}[/math]. Die Strecke [math] \overline{BC}[/math] steht senkrecht zu [math] \overline{AB}[/math] im Punkt B und hat die Länge [math] \frac{\overline{AB}}{2}[/math]. Der Kreis um D mit Radius [math] \overline{AD}[/math] ergibt Punkt E, welche auf der Verlängerung der Strecke [math] \overline{BD}[/math] liegt. Der Kreis um B mit Radius [math] \overline{BE}[/math] teilt die Strecke [math] \overline{AB}[/math] im Verhältnis des Goldenen Schnitts.

Äußere Teilung

	"klassische Methode"
	George Odom

Goldener Schnitt im Pentagramm

Goldenes Rechteck

Goldenes Dreieck(2 Möglichkeiten)

Goldener Winkel

Goldene Geometrie

Goldenes Rechteck

Goldenes Rechteck

Unter einem Goldenen Rechteck verstehen wir das Rechteck mit dem Seitenverhältnis des Goldenen Schnittes. Das bedeutet die Seiten a und b stehen im Verhältnis [math] \frac{a}{b} = \frac{a+b}{a} \\ [/math].

Konstruiert wird das Goldene Rechtecks durch eine abgewandelte Form der Konstruktion. Durch die innere Konstruktion findet man den Punkt der die Strecke im Goldenen Schnitt teilt. Nun ist die längere Teilstrecke, im Bild die Strecke a, die Höhe des Rechtecks und wir können es vervollständigen.

Eine Besonderheit des Goldenen Rechtecks ist, dass man immer ein Goldenes Rechteck erhält wenn man von einem Goldenen Rechteck ein größtmögliches Quadrat abschneidet. In dem Bild gibt also das kleinere rote Rechteckt wieder ein Goldenes Rechteck. Dies kann beliebig oft wiederholt werden.

Goldene Spirale

Goldene Spirale

Wenn wir ein Goldenes Rechteck in ein größtmögliches Quadrat und ein kleineres Goldenes Rechteck einteilen und dies bei dem kleineren wiederholen und immer bei dem kleineren Rechteck so machen, entsteht eine endlose Folge. Zeichnen wir jetzt ,in die Quadrate, in geeigneter Weise Viertelkreise ein, entsteht eine Spirale, die eine gute Approximation der logarithmischen Spirale ist. Der Mittelpunkt der Spirale liegt auf dem Schnittpunkt der Diagonalen des ersten und des zweiten Goldenen Rechtecks. Besonders ist auch der Zusammenhang mit der Fibonacci-Folge, da die Radien der Kreissektoren genau der Folge entspricht.

Goldene Dreiecke

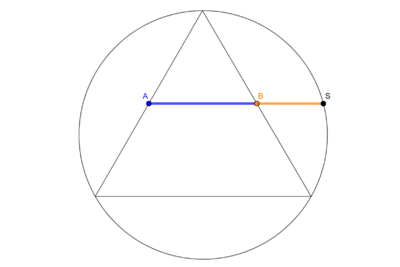
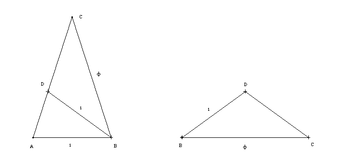
Goldene Dreiecke

Es gibt zwei unterschiedliche Arten des Goldenes Dreiecks, ein spitzes (erster Art) und ein stumpfes (zweiter Art). Beides sind gleichschenklige Dreiecke, bei denen ein Schenkel zur Grundseite im Goldenen Schnitt steht.

Beim Goldenen Dreieck erster Art, bilden die Schenkel die Majoren, also die längere Teilstrecke, und die Grundseite ist der Minor. Die beiden Winkel die an die Grundseite grenzen haben 72° und der dritte 36°. Das Goldene Dreieck zweiter Art hat zwei Minoren, die Schenkel, und die Basiswinkel haben jeweils 36° während der dritte Winkel 108° hat.

Insbesondere können wir vom Goldenen Dreieck erster Art ein größtmögliches Goldenes Dreieck zweiter Art abschneiden und zurück bleibt ein Goldenes Dreieck erster Art.

Goldener Winkel

Goldener Winkel

Teilt man einen Kreisumfang im Goldenen Schnitt, ergibt sich ein Winkel von 137,5°. Dies erreichen wir durch [math]  2\pi - \frac{2\pi}{\Phi}  \approx  3,88 \approx 222,5°\\\\\\[/math]

%Goldener Schnitt in der Geschichte

Die erste genaue Beschreibung des Goldenen Schnitts stammt von Euklid %verlinkung?% (325-270 v.Chr.), jedoch ist umstritten ob die Entdeckung auf ihn oder auf einen früheren Mathematiker zurückzuführen ist. %(Hippasos von Metapont (spätes 6. Jahrhundert v. Chr.) oder auf Eudoxos von Knidos (um 370 v. Chr.))

An Popularität gewann er allerdings erst ab Mitte des 19. Jahrhunderts.

%Goldener Schnitt in Natur und Technik

Der Goldene Schnitt ist an vielen Stellen in der Natur zu beobachten, am einfachsten jedoch in der Pflanzenwelt. Viele Pflanzen stellen ihre Blätter im Goldenen Winkel zueinander auf, aus einem praktischen Grund: Durch diesen speziellen Winkel überlappen sich so wenig Blätter wie möglich, sodass die Pflanze die maximale Sonnenenergie aufnehmen kann.

Blütenstand der Sonnenblume

Bei der Sonnenblume lässt sich beobachten, dass die Blüten in der Form von rechts- und linksdrehenden Spiralen angeordnet sind. Das Interessante hieran ist, dass die Anzahl der jeweiligen Spiralen immer zwei aufeinander folgenden Fibonacci-Zahlen entspricht und der Winkelversatz der Spiralen immer dem Goldenen Winkel φ bzw. einer Ableitung dessen.

%Website http://www.3d-meier.de/tut22/Sonne/Seite1.html#:~:text=In%20der%20Sonnenblume%20sind%20die%20Kerne%20in%20Spiralen%20angeordnet.&text=Die%20Anordnung%20der%20Kerne%20in,sich%20vom%20Goldenen%20Schnitt%20ableitet.

%Bahnresonanzen

%Schwarze Löcher

%Kristallstrukturen

Goldener Schnitt in Architektur

Leipziger Rathaus

Kölner Dom

Parthenon

Petersbasilika

Technik

Der Goldene Schnitt taucht unter anderem beim Geigenbau %(https://www.michael-holzapfel.de/themen/goldenerschnitt/gs-geige/geige.htm) und beim Bau von Ultraleichtflugzeugen %(https://www.imw.tu-clausthal.de/fileadmin/IMW/documents/Institutsmitteilungen/1998/98_31.pdf Seite 3/4) auf.