Hilberts Hotel: Unterschied zwischen den Versionen
Fx255 (Diskussion | Beiträge) |
Fx255 (Diskussion | Beiträge) |
||
| Zeile 36: | Zeile 36: | ||
Diese Bijektion kann auch als Abbildung von den natürlichen Zahlen mit der Null in die Natürlichen Zahlen ohne die Null geschrieben werden.[[Datei:Ein Gast 2.jpg|alternativtext=0 auf 1, 1 auf 2, 2 auf 3, allg. n auf n+1|ohne|mini|Abbildung von N mit Null in N ohne Null]] | Diese Bijektion kann auch als Abbildung von den natürlichen Zahlen mit der Null in die Natürlichen Zahlen ohne die Null geschrieben werden.[[Datei:Ein Gast 2.jpg|alternativtext=0 auf 1, 1 auf 2, 2 auf 3, allg. n auf n+1|ohne|mini|Abbildung von N mit Null in N ohne Null]] | ||
| − | Das bedeutet nach der Definition von Gleichmächtigkeit in 2, die Natürlichen Zahlen mit 0 sind Gleichmächtig zu den natürlichen Zahlen ohne die Null | + | Das bedeutet nach der Definition von Gleichmächtigkeit in [https://funfacts.mathi.uni-heidelberg.de/index.php/Hilberts_Hotel#2_Mathematisches_Vorwissen.2FHintergrund 2], die Natürlichen Zahlen mit 0 sind Gleichmächtig zu den natürlichen Zahlen ohne die Null |
<math> |\mathbb{N}| = |\mathbb{N_0}| </math> | <math> |\mathbb{N}| = |\mathbb{N_0}| </math> | ||
Oder auch <math> \infty+1=\infty </math> | Oder auch <math> \infty+1=\infty </math> | ||
|} | |} | ||
Version vom 12. März 2021, 11:29 Uhr
1 Einführung
Hilberts Hotel ist ein Gedankenexperiment zur Veranschaulichung von Unendlichkeiten. Es wurde vom Deutschen Mathematiker David Hilbert entwickelt.
2 Mathematisches Vorwissen/Hintergrund
Eine Bijektion ist eine Abbildung zwischen zwei Mengen M und N, die jedem Element m aus M [math]( m \in M )[/math] genau ein Element n aus N [math]( n \in N )[/math] zuordnet.
Zwei Mengen heißen gleichmächtig, falls es eine Bijektion zwischen ihnen gibt.
[math] \mid \text{ } M\mid = \mid N\mid \Leftrightarrow \exists \text{ } f: M \to N[/math], so dass f bijektiv
Eine Menge M heißt abzählbar, wenn sie Gleichmächtig zu den natürlichen Zahlen [math] \mathbb{N}[/math] ist.
[math] M \text{ abzählbar} \Leftrightarrow \mid M\mid = \mid \mathbb{N} \text{ } \mid [/math]
Eine Menge M heißt unendlich, wenn sie gleichmächtig zu einer echten Teilmenge von sich selbst ist.
[math] M \text{ unendlich} \Leftrightarrow \mid M\mid = \mid L\mid, L \subset M [/math]
3 Hilberts Hotel
3.1 Ein Gast
Stell dir vor du hast Ferien und möchtest in den Urlaub Fahren. Die ersten Hotels bei denen du ankommst sind leider alle schon voll belegt. Nun stehts du vor Hilberts Hotel, dessen Zimmer auch alle voll belegt sind. Du willst gerade weiterfahren um am nächsten Hotel dein Glück zu versuchen, da kommt der Portier mit einem Vorschlag auf dich zu. Du hast Glück, denn bei Hilberts Hotel handelt es sich nicht um ein "normales" Hotel. Es gibt zwar auch ein Lobby, und Angestellte und vielleicht sogar einen Pool, aber im Gegensatz zu "normalen" Hotels hat Hilberts Hotel unendlich viele Zimmer, die mit den Natürlichen Zahlen [1,2,3,4,...] durchnummeriert sind. Nun weißt du, dass das Hotel unendlich viele Zimmer hat, aber du weißt ja auch dass es bereits voll ist, also unendlich viele Gäste im Hotel untergebracht sind.
Frage: Wie kannst du trotzdem einen Platz in einem Zimmer bekommen?
| Antwort |
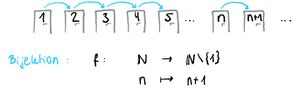
| Der Portier schlägt dir vor, dass jeder Gast in das nächste Zimmer zieht, sodass das erste Zimmer für dich frei wird. Da es sich bei Hilberts Hotel um ein unendliches Hotel mit unendlich vielen Zimmern Handelt gibt es keinen letzten Gast. Somit findet jeder Gast ein neues Zimmer und das erste Zimmer wird frei. Du kannst also entspannt Urlaub machen und musst dich nicht mehr um deine Unterkunft sorgen.
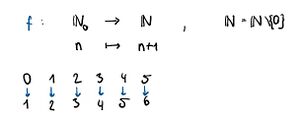
Diese Bijektion kann auch als Abbildung von den natürlichen Zahlen mit der Null in die Natürlichen Zahlen ohne die Null geschrieben werden.
Das bedeutet nach der Definition von Gleichmächtigkeit in 2, die Natürlichen Zahlen mit 0 sind Gleichmächtig zu den natürlichen Zahlen ohne die Null [math] |\mathbb{N}| = |\mathbb{N_0}| [/math] Oder auch [math] \infty+1=\infty [/math] |