Goldener Schnitt: Unterschied zwischen den Versionen
Seb Sp (Diskussion | Beiträge) |
Seb Sp (Diskussion | Beiträge) |
||
| Zeile 181: | Zeile 181: | ||
\end{align*} | \end{align*} | ||
| − | </math> | + | </math> <ref>Funfacts Vorlesung; Universität Heidelberg; Wintersemester 20/21</ref> |
(Ist gleich der Gleichung des goldenen Schnitts) | (Ist gleich der Gleichung des goldenen Schnitts) | ||
Version vom 26. März 2021, 20:20 Uhr
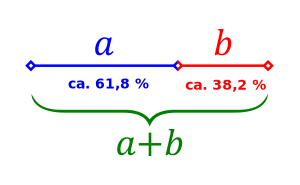
Der "Goldene Schnitt" bezeichnet allgemein ein spezielles Teilungsverhältnis einer Strecke.
Die Besonderheit dieses Verhältnisses besteht darin, die Gesamtstrecke in zwei Teile aufzuteilen, wobei die Gesamtstrecke dasselbe Teilungsverhältnis zur größeren Teilstrecke aufweist, wie auch die größere Teilstrecke zur kleineren Teilstrecke.
Den Quotient der Strecken nennt man die Goldene Zahl [math]\Phi[/math].
Herleitung des Goldenen Schnitts
Die obige Definition lässt sich algebraisch ausdrücken und wie folgt eindeutig lösen:
- [math] \Phi = \frac{a}{b} = \frac{a+b}{a} = 1+\frac{b}{a} = 1 + \frac{1}{\Phi}\\\\ [/math]
- [math] \Leftrightarrow \Phi^{2} = \Phi + 1 \\\\ [/math]
- [math] \Leftrightarrow 0 = \Phi^{2} - \Phi - 1 \\\\ [/math]
- [math] \Rightarrow \Phi_{1} = \frac{1+\sqrt[]{5}}{2} \approx 1,618\\ [/math]
- [math] \Rightarrow \Phi_{2} = \frac{1-\sqrt[]{5}}{2} \approx 0,618 = \frac{1}{\Phi_{1}} [/math]
Wir nennen [math] \Phi_{1} [/math] die Goldene Zahl [math] \Phi [/math] mit den Kehrwert [math] \frac{1}{\Phi}= \Phi - 1 [/math]
[math]\Phi[/math] als "irrationalste" Zahl
Allgemein gibt es keine irrationale Zahl die "irrationaler" als eine andere irrationale Zahl ist. [math]\Phi[/math] lässt sich nur sehr "langsam" durch rationale Zahlen annähern, daher die meist scherzhafte Aussage [math]\Phi[/math] sei die "irrationalste" Zahl.
Kettenbruchdarstellung
Um die Annäherung durch rationale Zahlen vorzunehmen, stellt man die Zahl als unendlichen Kettenbruch dar und bricht diesen an einer Stelle ab. Je später, desto genauer die Annäherung. (mehr )
- [math] \Phi = 1 + \frac{1}{\Phi} = 1 + \frac{1}{1 + \frac{1}{\Phi}} = 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{\Phi}}} = 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{\Phi}}}} \quad ... [/math]
Wir sehen nun, dass der Kettenbruch von [math]\Phi[/math] nur Einsen als Elemente enthält, woraus sich wiederum folgern lässt, dass der Nenner der Näherung durch rationale Zahlen so langsam wie nur möglich wächst und sich somit eine möglichst genaue Approximation nur schlecht durchzuführen ist.
Daher die Aussage [math]\Phi[/math] sei die irrationalste nur mögliche Zahl.
Sehr interessant ist hierbei, dass der Näherungsbruch immer aus zwei aufeinanderfolgenden Fibonacci-Zahlen besteht!
| Abbruch nach n Elementen | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | [math]\vdots[/math] | Die rekursive Bildungsformel lautet: [math] \frac{p_{n}}{q_{n}} = \frac{p_{n-1} + q_{n-1}}{p_{n-1}} [/math] |
|---|---|---|---|---|---|---|---|---|---|---|
| Näherungswert | 2 | [math] \frac{3}{2} [/math] | [math] \frac{5}{3} [/math] | [math] \frac{8}{5} [/math] | [math] \frac{13}{8} [/math] | [math] \frac{21}{13} [/math] | [math] \frac{34}{21} [/math] | [math] \frac{55}{34} [/math] | ||
| Abweichung von [math] \Phi [/math] in % | 23,6 | 7,3 | 3 | 1,1 | 0,43 | 0,16 | 0,062 | 0,024 |
Kettenwurzeldarstellung
Alternativ lässt sich [math]\Phi[/math] auch durch eine unendliche Kettenwurzel nähern, dies folgt aus [math]\Phi^{2} = \Phi + 1[/math]
- [math] \Phi = \sqrt{1+\sqrt{1+\sqrt{1+\sqrt{1+...}}}} [/math]
Geometrische Konstruktion von [math]\Phi[/math]
Unterschieden wird die geometrische Konstruktion in innere und äußere Teilung. Die innere Teilung teilt eine gegebene Strecke im goldenen Schnitt, wohingegen die äußere Teilung zu einer gegebenen Strecke eine weitere außerhalb liegende Strecke konstruiert, sodass die Beiden im goldenen Verhältnis zueinander stehen.
Innere Teilung
| "klassische Methode" zur inneren Teilung:
Gegeben sei eine beliebige Länge [math] \overline{AB}[/math]. Die Strecke [math] \overline{BC}[/math] steht senkrecht zu [math] \overline{AB}[/math] im Punkt B und hat die Länge [math] \frac{\overline{AB}}{2}[/math]. Der Kreis um C mit Radius [math] \overline{BC}[/math] schneidet die Strecke [math] \overline{AC}[/math] im Punkt D. Der Kreis um A mit Radius [math] \overline{AD}[/math] teilt die Strecke [math] \overline{AB}[/math] im Verhältnis des Goldenen Schnitts. | |
| Methode nach Euklid:
Gegeben sei eine beliebige Länge [math] \overline{AB}[/math]. Die Strecke [math] \overline{BC}[/math] steht senkrecht zu [math] \overline{AB}[/math] im Punkt B und hat die Länge [math] \frac{\overline{AB}}{2}[/math]. Der Kreis um D mit Radius [math] \overline{AD}[/math] ergibt Punkt E, welche auf der Verlängerung der Strecke [math] \overline{BD}[/math] liegt. Der Kreis um B mit Radius [math] \overline{BE}[/math] teilt die Strecke [math] \overline{AB}[/math] im Verhältnis des Goldenen Schnitts. |
Äußere Teilung
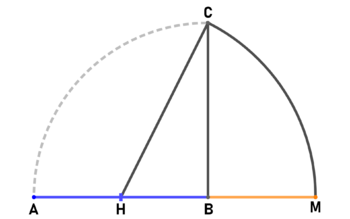
| "klassische Methode" zur äußeren Teilung:
Gegeben ist eine Strecke [math] \overline{AB}[/math]. Die Strecke [math] \overline{BC}[/math] hat die gleiche Länge wie [math] \overline{AB}[/math] und steht senkrecht auf Punkt B. Der Punkt teilt Strecke [math] \overline{AB}[/math] in der Hälfte. Der Kreis um Punkt H mit Radius [math] \overline{BC}[/math] schneidet die Verlängerung von [math] \overline{AB}[/math] im Punkt M. Punkt B teilt nun die Strecke [math] \overline{AM}[/math] im goldenen Schnitt. | |
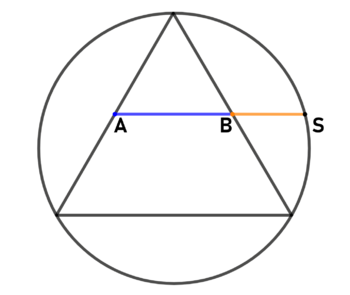
| Methode nach George Odom:
Gegeben sei ein gleichseitiges Dreieck mit Umkreis. Teilt man nun zwei Seiten des Dreiecks in der Mitte und verbindet die Punkte (A, B) so ergibt die Verlängerung von [math] \overline{AB}[/math] einen Schnittpunkt S mit dem Umkreis. Punkt B teilt nun die Strecke [math] \overline{AS}[/math] im goldenen Schnitt. |
Goldene Geometrie
Goldenes Rechteck
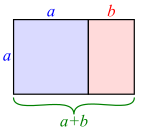
Unter einem Goldenen Rechteck verstehen wir das Rechteck mit dem Seitenverhältnis des Goldenen Schnittes. [1]Das bedeutet die Seiten a und b stehen im Verhältnis [math] \frac{a}{b} = \frac{a+b}{a} \\ [/math].
Konstruiert wird das Goldene Rechtecks durch eine abgewandelte Form der Konstruktion. Durch die innere Konstruktion findet man den Punkt der die Strecke im Goldenen Schnitt teilt. Nun ist die längere Teilstrecke, im Bild die Strecke a, die Höhe des Rechtecks und wir können es vervollständigen. [2]
Eine Besonderheit des Goldenen Rechtecks ist, dass man immer ein Goldenes Rechteck erhält wenn man von einem Goldenen Rechteck ein größtmögliches Quadrat abschneidet. In dem Bild gibt also das kleinere rote Rechteckt wieder ein Goldenes Rechteck. Dies kann beliebig oft wiederholt werden. [3]
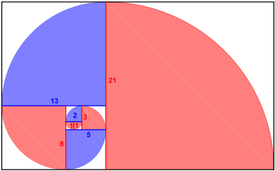
Goldene Spirale
Wenn wir ein Goldenes Rechteck in ein größtmögliches Quadrat und ein kleineres Goldenes Rechteck einteilen und dies bei dem kleineren wiederholen und immer bei dem kleineren Rechteck so machen, entsteht eine endlose Folge. Zeichnen wir jetzt ,in die Quadrate, in geeigneter Weise Viertelkreise ein, entsteht eine Spirale, die eine gute Approximation der logarithmischen Spirale ist. Der Mittelpunkt der Spirale liegt auf dem Schnittpunkt der Diagonalen des ersten und des zweiten Goldenen Rechtecks. [4] Besonders ist auch der Zusammenhang mit der Fibonacci-Folge, da die Radien der Kreissektoren genau der Folge entspricht. [5]
Goldene Dreiecke
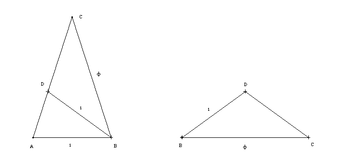
Es gibt zwei unterschiedliche Arten des Goldenes Dreiecks, ein spitzes (erster Art) und ein stumpfes (zweiter Art). Beides sind gleichschenklige Dreiecke, bei denen ein Schenkel zur Grundseite im Goldenen Schnitt steht. [6]
Beim Goldenen Dreieck erster Art, bilden die Schenkel die Majoren, also die längere Teilstrecke, und die Grundseite ist der Minor. Die beiden Winkel die an die Grundseite grenzen haben 72° und der dritte 36°. Das Goldene Dreieck zweiter Art hat zwei Minoren, die Schenkel, und die Basiswinkel haben jeweils 36° während der dritte Winkel 108° hat. [7]
Herleitung: Mit [math]\frac{k}{a}=\Phi[/math] können wir auch die Winkel im Dreieck berechnen:
[math] \begin{align*} \cos(\alpha) &= \frac{\frac{a}{2}}{k} = \frac{a}{2k} = \frac{1}{2\Phi}\\ \Leftrightarrow \alpha &= 72°\\ \end{align*} [/math]
Damit bekommen wir:
[math] \begin{align*} 180° - 90° - 72° = 18° \rightarrow \beta &= 36° \\ \text{oder:}\quad \beta = \quad 2 \sin\left(\frac{1}{2\Phi}\right) &= 36° \end{align*} [/math]
Im stumpfwinkligen Dreieck bekommen wir noch einen Winkel: [math]180° - 2 \cdot 36° = 108°[/math]
Insbesondere können wir vom Goldenen Dreieck erster Art ein größtmögliches Goldenes Dreieck zweiter Art abschneiden und zurück bleibt ein Goldenes Dreieck erster Art. [8]
Konstriktion goldener Schnitt mit innerer und äußeren Teilung
Es gibt bei der Konstruktion des goldenen Schnitts stehts zwei Möglichkeiten daran zu gehen. Es gibt Varianten, die sich mit dem inneren und welche die sich mit dem äußeren Verhältnis beschäftigen. Innere varianten nehmen eine Stecke und teilen die im goldenen Schnitt. Die äußeren Varianten konstruieren zu einer gegebenen Strecke a eine Teilstrecke b, sodass die beiden im goldenen Verhältnis zueinander stehen. Die einfachste Konstruktion des goldenen Schnittes ist über ein Dreieck. Man zeichne zuerst die Grundseite k ([math]\overline{AB}[/math]) und teilt diese in der Hälfte. Wir bekommen nun 2 Strecken mit der Länge k/2. Als nächstes zeichnen wir orthogonal zu B eine Strecke mit der Länge k/2 ([math]\overline{BC}[/math]) und vervollständigen das Dreicek. Als nächstes konstruieren wir einen Kreis (L) um C herum mit dem Radius k/2. Zum Schluss zeichnen wir um A einen Kreis(M), der vom Radius den Schnittpunkt von dem Kreis L mit [math]\overline{AC}[/math] besitzt bzw. [math]r_M= \overline{AC}-k/2[/math]. Der Schnittpunkt des Kreises M und [math]\overline{AB}[/math] teilt die Strecke [math]\overline{AB}[/math] im goldenen Verhältnis. Wir wissen: [math] \frac{a}{b}= \phi [/math]. Beweis:
[math] \begin{align*} k &=a+b\\ k^2+\left( \frac{k}{2}\right)^2 &= \left( a+ \frac{k}{2} \right)^2\\ \Leftrightarrow k^2+\frac{k^2}{4} &= a^2 + ak+ \frac{k^2}{4}| \text{ersetze k durch a+b} \\ \Leftrightarrow a^2 + 2ab + b^2 &= a^2 + a^2 + ab\\ \Leftrightarrow b^2 + ab &= a^2 \ \end{align*} [/math] [9]
(Ist gleich der Gleichung des goldenen Schnitts) mit inneren Teilung konstruiert.
Desweiteren können wir auch das Verhältnis des goldenen Schnitts durch äußere Teilung bekommen.
Zunächst zeichnen wir eine Stecke [math]\overline{AB}[/math] mit der Länge a. Am Punkt B zeichnen wir orthogonal eine Strecke [math]\overline{BC}[/math] auch mit der Länge a. Nun wird der Punkt C mit dem Mittelpunkt M von [math]\overline{AB}[/math] verbunden. [math]\overline{CM}[/math] bildet den Radius eines Kreises. [math]\overline{AB}[/math] wird in Richtung des Kreises verlängert zum Punkt D. [math]\overline{BD}[/math] bildet unser b. Auch hier gilt wieder [math]\frac{a}{b}= \Phi[/math]
Beweis: Wir wissen, dass [math]\overline{AB} = \overline{BC}=a[/math] und [math]\overline{AM}=\frac{a}{2}[/math] und k = a + b mit [math]\frac{a}{b}= \Phi[/math]
[math] \begin{align*} \Rightarrow \overline{CM} = \sqrt{\left(\frac{a}{2}\right)^2+a^2} = \sqrt{\frac{5 a^2}{4}} = \sqrt{\frac{5}{4}}a\\ \Rightarrow k = a + b = \frac{a}{2} + \sqrt{\frac{5}{4}}a= a + \sqrt{\frac{5}{4}} a - \frac{a}{2}a \\ \Rightarrow \Phi =\frac{a}{b} \hat{=} \frac{a}{\sqrt{\frac{5}{4}}a-\frac{a}{2}} = \frac{1}{\sqrt{\frac{5}{4}}-\frac{1}{2}} =1,61803... = \Phi \end{align*} [/math]
Goldener Winkel
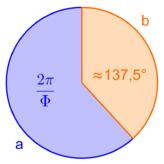
Der goldene Winkel ist beispielsweise in der Natur relevant. Man betrachtet einen Kreis und teilt ihn in 2 Segmente, so dass der eine Teilumfang a und der andere b im goldenen Verhältnis stehen. Dabei ergibt sich ein Winkel indem man den Vollwinkel durch den goldenen Schnitt teilt [math]\frac{2 \pi}{\Phi} \approx 222,5°[/math] Und [math]2\pi - \frac{2 \pi}{\Phi} \approx 137,5 = \Psi [/math]
Um viel Licht abzubekommen, versuchen Pflanzen ihre Blätter so zu legen, dass möglichst wenige übereinander liegen.
Um anzugeben, wie oft ich ein weiteres Blatt um einen gewissen Winkel [math]\alpha[/math] verschiebe, bis ein Blatt ein anderes wieder verdeckt, hilft folgende Formel:
[math] \begin{align*} n \cdot \alpha = k \cdot 360° \quad \Leftrightarrow \alpha = \frac{k}{n}360°\quad k,n \in \mathbb{N} \end{align*} [/math]
n gibt an, wie viele Blätter ich hinzufügen kann; k gibt ein vielfaches von 360° an.
Optimal für eine Pflanze ist also das kleinste n für das die Formel erfüllt werden kann, groß ist, da so die Pflanze viel Licht bekommt. Wenn [math]\alpha[/math] irrational ist, kann es schlecht bis gar nicht als Bruch dargestellt werden. Je irrationaler eine Zahl also ist, dann sie umso schlechter als Bruch angenähert werden. Mit der Bedingung bietet sich die irrationalste Zahl [math]\Phi[/math] an bzw als Winkel [math]\Psi[/math]. [10]
Pentagramm
Zuerst nimmt man ein regelmäßiges Fünfeck und zeichnet die diagonalen ein. Die Diagonalen formen einen Stern mit fünf Zacken. Jedes gleichschenklige Dreieck, was sich im Pentagon bildet, ist ein goldenes Dreieck. Die Diagonalen teilen die Seiten im goldenen Verhältnis. Die Winkelsumme in einem Pentagon ist 540° und in jeder Ecke sind 3 gleich große Winkel mit je 36°. Wie beim goldenen Dreieck. [11]
%Goldener Schnitt in der Geschichte
Die erste genaue Beschreibung des Goldenen Schnitts stammt von Euklid %verlinkung?% (325-270 v.Chr.), jedoch ist umstritten ob die Entdeckung auf ihn oder auf einen früheren Mathematiker zurückzuführen ist. %(Hippasos von Metapont (spätes 6. Jahrhundert v. Chr.) oder auf Eudoxos von Knidos (um 370 v. Chr.))
An Popularität gewann er allerdings erst ab Mitte des 19. Jahrhunderts.
Der Goldener Schnitt in der Architektur
Leipziger Rathaus
Beim Bau des alten Leipziger Rathauses ließ der Architekt Hieronymus Lotter den Turmeingang und Turm so positionieren, dass er die Vorderfront des Gebäudes im Verhältnis des goldenen Schnitts teilte. Kunst und Architektur wurden zu dieser Zeit geprägt von den Merkmalen der Renaissance, wie in diesem Fall mathematische Klarheit und Schönheit. [12] Das alte Rathaus erhielt dadurch die bis heute erkennbare asymmetrische Fassade die seitdem ein Wahrzeichen der Stadt ist.
Kölner Dom
Parthenon
Petersbasilika
Der Goldene Schnitt ist an vielen Stellen in der Natur zu beobachten, am einfachsten jedoch in der Pflanzenwelt. Viele Pflanzen stellen ihre Blätter im Goldenen Winkel zueinander auf, aus einem praktischen Grund: Durch diesen speziellen Winkel überlappen sich so wenig Blätter wie möglich, sodass die Pflanze die maximale Sonnenenergie aufnehmen kann.
Blütenstand der Sonnenblume
Bei der Sonnenblume lässt sich beobachten, dass die Blüten in der Form von rechts- und linksdrehenden Spiralen angeordnet sind. Das Interessante hieran ist, dass die Anzahl der jeweiligen Spiralen immer zwei aufeinander folgenden Fibonacci-Zahlen entspricht und der Winkelversatz der Spiralen immer dem Goldenen Winkel φ bzw. einer Ableitung dessen.
%Bahnresonanzen
%Schwarze Löcher
%Kristallstrukturen
Technik
Der Goldene Schnitt taucht unter anderem beim Geigenbau %(https://www.michael-holzapfel.de/themen/goldenerschnitt/gs-geige/geige.htm) und beim Bau von Ultraleichtflugzeugen %(https://www.imw.tu-clausthal.de/fileadmin/IMW/documents/Institutsmitteilungen/1998/98_31.pdf Seite 3/4) auf.
Der Goldene Schnitt in der Kunst
In der Kunst wird der Goldene Schnitt durch Konstruktion verwendet, um eine harmonische und schöne Wirkung zu erzielen. Ob nun Goldene Figuren, wie das Goldene Rechteck, oder der Goldene Schnitt als Verhältnis der Proportionen angewendet wird, eins ist meistens gleich, die Wirkung. Auch wenn einige Studien zu der angeblichen Schönheit des Goldenen Schnittes existieren gibt es auch viele Zweifel daran. [13]
Empfinden des Goldenen Schnitts
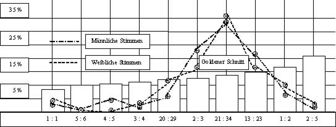
Fechner hat mithilfe dreier verschiedener Methoden herauszufinden gesucht, ob der Goldene Schnitt tatsächlich bevorzugt wird. Diese Methoden waren die der Wahl, der Herstellung und der Verwendung. [14] Bei der Methode der Wahl legte er den Probanden weiße Rechtecke vor und tatsächlich hat sich eine Bevorzugung jener Rechtecke herausgestellt die als Seitenverhältnis annähernd den Goldenen Schnitt haben. [15]
Quellen
- ↑ Walser, Hans, Der Goldene Schnitt, Eagle Einblicke, Leipzig, 2009, 5.Auflage, Seite 39
- ↑ Walser, Hans, Der Goldene Schnitt, Eagle Einblicke, Leipzig, 2009, 5.Auflage, Seite 39
- ↑ Walser, Hans, Der Goldene Schnitt, Eagle Einblicke, Leipzig, 2009, 5.Auflage, Seite 40
- ↑ Beutelspacher, Albrecht, Petri, Bernhard, Der Goldene Schnitt, B.I. Wissenschaftsverlag, 1989, Seite 57
- ↑ Ausarbeitung Goldene Spirale (ph-freiburg.de)
- ↑ Walser, Hans, Der Goldene Schnitt, Eagle Einblicke, Leipzig, 2009, 5.Auflage, Seite 51
- ↑ Walser, Hans, Der Goldene Schnitt, Eagle Einblicke, Leipzig, 2009, 5.Auflage, Seite 51
- ↑ Walser, Hans, Der Goldene Schnitt, Eagle Einblicke, Leipzig, 2009, 5.Auflage, Seite 51
- ↑ Funfacts Vorlesung; Universität Heidelberg; Wintersemester 20/21
- ↑ Funfacts Vorlesung; Universität Heidelberg; Wintersemester 20/21
- ↑ https://christianrohrbach.net/wp-content/uploads/42-Goldener-Schnitt-Pentagramm.pdf
- ↑ https://www.planet-wissen.de/natur/forschung/mathematik/pwiedergoldeneschnitt100.html
- ↑ Der goldene Schnitt in der Kunst (goldener-schnitt.info)
- ↑ Fechner, Gustav, Zur experimentalen Ästhetik, Hirzel, Leipzig, 1871, Seite 50
- ↑ Schoot, Albert van der, Die Geschichte des Goldenen Schnitts, Aufstieg und Fall der göttlichen Proportion, Frommann-Holzboog, Stuttgart, 2005, Seite 215-225