Euklidischer Algorithmus und Kettenbrüche: Unterschied zwischen den Versionen
| Zeile 122: | Zeile 122: | ||
== Geometrische Visualisierung von regulären Kettenbrüchen == | == Geometrische Visualisierung von regulären Kettenbrüchen == | ||
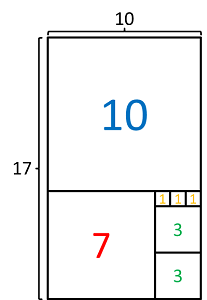
| − | [[Datei:Bild17-10.png|right|thumb|Bruch 1: <math>\frac{17}{10}</math>]] | + | [[Datei:Bild17-10.png|right|thumb|Bruch 1: <math>\frac{17}{10}</math>]]<ref name="Bild 1: 17/10"> Bild wurde selbst hergestellt </ref> |
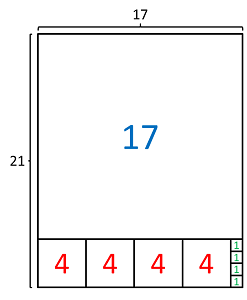
| − | [[Datei:Bild21-17.png|right|thumb|Bruch 2: <math>\frac{21}{17}</math>]] | + | [[Datei:Bild21-17.png|right|thumb|Bruch 2: <math>\frac{21}{17}</math>]]<ref name="Bild 1: 21/17"> Bild wurde selbst hergestellt </ref> |
Der behandelte und bewiesene Algorithmus zum berechnen der Kettenbruchdarstellung einer rationalen Zahl lässt sich auch visuell darstellen. | Der behandelte und bewiesene Algorithmus zum berechnen der Kettenbruchdarstellung einer rationalen Zahl lässt sich auch visuell darstellen. | ||
Version vom 30. März 2021, 20:54 Uhr
Diese Seite behandelt den simplen, aber zugleich genialen Euklidischen Algorithmus und wie dieser mit der Kettenbruchdarstellung rationaler und irrationaler Zahlen zusammenhängt.
Der Euklidische Algorithmus
Schon 300 vor Christus befasste sich Euklid in seinem berühmten Werk "Die Elemente" mit der Frage, wie man das größte gemeinsame Maß, also den größten gemeinsamen Teiler ([math] ggT [/math]) zweier Zahlen finden kann.
Er entwickelte dazu einen Algorithmus, der auf folgendem Lemma beruht:
Lemma: Es seien [math] a, b \in \mathbb{N} [/math] und [math] b \gt 0 [/math] mit
- [math] a = bq + r, \hspace{20pt} 0 \le r \lt b [/math]
Dann gilt:[math] \hspace{10pt} ggT(a, b) = ggT(b, r). [/math]
| [math] a = bq + r [/math], also ist jeder gemeinsame Teiler von [math] b [/math] und [math] r [/math] auch ein Teiler von
[math] a [/math]. Stellt man die Gleichung nach [math] r [/math] um, erhält man [math] r = a - bq [/math] und somit ist jeder gemeinsame Teiler von [math] a [/math] und [math] b [/math] auch ein Teiler von [math] r [/math]. Die Zahlenpaare [math] (a, b) [/math] und [math] (b, r) [/math] haben also die gleichen gemeinsamen Teiler und somit auch den gleichen [math] ggT [/math]. |
Funktionsweise
Gesucht ist nun also der größte gemeinsame Teiler zweier ganzer Zahlen [math] a [/math] und [math] b [/math]. Der Algorithmus funktioniert wie folgt:
- Teile [math] a [/math] durch [math] b [/math] und erhalten den Rest [math] r [/math].
- Ist [math] r = 0 [/math], ist a ohne Rest durch b teilbar und es gilt [math] ggT(a, b) = b [/math]. Ist [math] r \neq 0 [/math], ersetze [math] a [/math] durch [math] b [/math] und wiederhole Schritt 1.
- Führe die Schritte solange durch, bis [math] \text{Rest} \hspace{2pt} 0 [/math] bleibt.
Der letzte Rest, der von [math] 0 [/math] verschieden ist, ist der größte gemeinsame Teiler von [math] a [/math] und [math] b [/math].
| Gesucht ist der [math] ggT [/math] von [math] 22 [/math] und [math] 16 [/math] |
|---|
| 1. [math] \frac{22}{16} = 1 \hspace{10pt} \text{Rest} \hspace{5pt} 6 [/math]
2. Rest ungleich [math] 0 \Rightarrow [/math] Schritt 1 3. [math] \frac{16}{6} = 2 \hspace{10pt} \text{Rest} \hspace{5pt} 4 [/math] 4. [math] \frac{6}{4} = 1 \hspace{13pt} \text{Rest} \hspace{5pt} 2 [/math] 5. [math] \frac{4}{2} = 2 \hspace{13pt} \text{Rest} \hspace{5pt} 0 [/math] [math] \Rightarrow [/math] Der größte gemeinsame Teiler von [math] 22 [/math] und [math] 16 [/math] ist [math] 2 [/math]. |
Was sind Kettenbrüche?[1]
Bevor nun ein Zusammenhang zwischen dem Euklidischen Algorithmus und besagten Kettenbrüchen hergestellt werden kann, sollten zuerst ein paar Grundlegende Konzepte mit Notation eingeführt werden.
Ein (unendlicher(1)/endlicher(2)) Kettenbruch ist generell ein Konstrukt der Form:
[math] \hspace{10pt} [/math] [math] a_0 + \dfrac{b_1}{a_1 + \dfrac{b_2}{a_2 + \dfrac{b_3}{ \hspace{10pt} \ddots }}} \hspace{12pt} (1) [/math] [math] \hspace{10pt} [/math] oder [math] \hspace{10pt} [/math] [math] a_0 + \dfrac{b_1}{a_1 + \dfrac{b_2}{ a_{n-2} + \dfrac{\ddots}{ \hspace{10pt} a_{n-1} + \dfrac{b_n}{a_n}}}} \hspace{12pt} (2) [/math] [math] \hspace{10pt} [/math] [math] \hspace{10pt} [/math] mit [math] \hspace{20pt} a_i, b_j \in \mathbb{Z} \hspace{12pt} i \in \mathbb{N}_0 \hspace{12pt} j \in \mathbb{N}. [/math]
In unseren Beispielen reicht es jedoch aus, lediglich reguläre Kettenbrüche zu betrachten. Diese haben die Form:
[math] \hspace{10pt} [/math] [math] a_0 + \dfrac{1}{a_1 + \dfrac{1}{a_2 + \dfrac{1}{ \hspace{10pt} \ddots }}} \hspace{12pt} (a) [/math] [math] \hspace{10pt} [/math] oder [math] \hspace{10pt} [/math] [math] a_0 + \dfrac{1}{a_1 + \dfrac{1}{ a_{n-2} + \dfrac{\ddots}{ \hspace{10pt} a_{n-1} + \dfrac{1}{a_n}}}} \hspace{12pt} (b) [/math] [math] \hspace{10pt} [/math] [math] \hspace{10pt} [/math] mit [math] \hspace{20pt} a_0 \in \mathbb{Z} \hspace{12pt} a_i \in \mathbb{N} \hspace{12pt} i \in \mathbb{N}. [/math]
Wie man erkennen kann, ist ein regulärer Kettenbruch somit durch seine Koeffizienten [math] a_0 [/math] und [math] a_i [/math] eindeutig gegeben. Die gängige Notation für diese Art von Kettenbruch ist wie folgt:
- [math] (a): \hspace{12pt} \left\lt a_0; a_1, a_2, \dots \right\gt [/math]
- [math] (b): \hspace{13pt} \left\lt a_0; a_1, a_2, \dots, a_n \right\gt [/math]
Zusätzlich lässt sich im (un-)endlichen Fall auch der Abschnitt oder Partialbruch des Kettenbruchs definieren. Für [math] 0 \le k \le n [/math] (endlich) bzw. [math] k \ge 0 [/math] (unendlich) definiert man:
$$ s_k := \left< a_0; a_1, a_2, \dots, a_k \right> $$
mit dazugehörigem [math] \text{Rest} [/math] :
$$ r_k := \left< a_k; a_{k+1}, a_{k+2}, \dots, a_n \right> \hspace{20pt} \text{bzw.} \hspace{20pt} r_k := \left< a_k; a_{k+1}, a_{k+2}, \dots \right> $$
[math][/math]
Kettenbruchdarstellung rationaler Zahlen [1]
Satz: Eine reelle Zahl ist genau dann rational, wenn sie sich als endlichen Kettenbruch darstellen lässt.
Oder äquivalent: Eine reelle Zahl ist genau dann irrational, wenn ihre Kettenbruchdarstellung unendlich ist.
| AusklappenBeweis |
Beispiel
Als Beispiel betrachte [math] p = - \dfrac{75}{27} [/math].
Das Vorgehen ist analog zum euklidischen Algorithmus.
[math] -75 = -3 \cdot 27 + 6 [/math]
(Rest 6)
[math] \Rightarrow p = -3 + \dfrac{6}{27} = -3 + \dfrac{1}{\dfrac{27}{6}} [/math]
[math] 27 = 4 \cdot 6 + 3 [/math]
(Rest 3)
[math] \Rightarrow p = -3 + \dfrac{1}{4 + \dfrac{3}{6}} = -4 + \dfrac{1}{4 + \dfrac{1}{\dfrac{6}{3}}} [/math]
[math] 6 = 2 \cdot 3 + 0 [/math]
(Rest 0, also entspricht der vorherige Rest 3 dem [math] ggT(-75, 27) [/math] )
[math] \Rightarrow p = -3 + \dfrac{1}{4 + \dfrac{1}{2 + \dfrac{0}{3}}} = -3 + \dfrac{1}{4 + \dfrac{1}{2}} [/math]
(reguläre, endliche Kettenbruchdarstellung)
Geometrische Visualisierung von regulären Kettenbrüchen
Der behandelte und bewiesene Algorithmus zum berechnen der Kettenbruchdarstellung einer rationalen Zahl lässt sich auch visuell darstellen. Dafür stellt man den zu einer gegebenen Zahl [math] p \in \mathbb{Q} [/math] mit [math] p = \frac{k}{l}, \hspace{3pt} k,l \in \mathbb{N} [/math] gehörenden Bruch als Rechteck, mit der Höhe [math] k [/math] und der Länge [math] l [/math] dar. Zu beachten ist allerdings, dass die Visualisierung nur für positive Werte von [math] k [/math] und [math] l [/math] gut funktioniert (negative Seitenlängen ergeben keinen Sinn).
Dann wird nach folgendem Schema vorgegangen:
|
Beispiel 1: Gegebener Bruch: [math] \dfrac{17}{10} [/math]
$$ \dfrac{17}{10} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{7}{10} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{1}{\dfrac{10}{7}} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{1}{1 + \dfrac{3}{7}} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{1}{1 + \dfrac{1}{\dfrac{7}{3}}} \hspace{10pt} = \hspace{10pt} \color{Blue} 1 + \dfrac{1}{\color{Red} 1 + \dfrac{1}{\color{Green} 2 + \dfrac{1}{\color{Orange} 3}}} $$
Beispiel 2: Gegebener Bruch: [math] \dfrac{21}{17} [/math]
$$ \dfrac{21}{17} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{4}{17} \hspace{10pt} = \hspace{10pt} 1 + \dfrac{1}{\dfrac{17}{4}} \hspace{10pt} = \hspace{10pt} \color{Blue} 1 + \dfrac{1}{\color{Red} 4 + \dfrac{1}{\color{Green} 4}} $$
Kettenbruchdarstellungen irrationaler Zahlen
Wie im vorigen Abschnitt gezeigt, haben irrationale Zahlen unendliche Kettenbruchdarstellungen. Dabei gilt, dass der Wert eines unendlichen Kettenbruchs der Form [math] \left\lt a_0; a_1, a_2, \dots \right\gt [/math] festgelegt ist, als[4] [math] \lim \limits_{n \to \infty} \left\lt a_0; a_1, \dots, a_n \right\gt [/math] Im folgenden betrachten wir einige Beispiele solcher Kettenbruchdarstellungen:
Beweis für die Irrationalität von [math] \sqrt{10} [/math]
Wir wissen, dass eine Zahl genau dann rational ist, wenn ihre Kettenbruchdarstellung endlich ist. Daher können wir zeigen, ob eine Zahl rational ist, indem wir ihre Kettenbruchdarstellung berechnen.
[math] \begin{align} \sqrt{10} &= 3 + (\sqrt{10} - 3) = 3 + \dfrac{(\sqrt{10} - 3)(\sqrt{10} + 3)}{3 + \sqrt{10}} = 3 + \dfrac{1}{3 + \sqrt{10}} \\ \\ &= 3 + \dfrac{1}{3+3+\dfrac{1} {3 + \sqrt{10}}} = 3 + \dfrac{1}{6+\dfrac{1} {3 + \sqrt{10}}} \\ \\ &= 3 + \dfrac{1}{6+\dfrac{1} {6 + \dfrac{1} {3 + \sqrt{10}}}} \\ \\ &= 3 + \dfrac{1}{6+\dfrac{1} {6 + \dfrac{1} {6 + \dfrac{1} {\hspace{10pt} \ddots}}}} \end{align} [/math]
Diese Darstellung bricht nie ab; [math] \sqrt{10} [/math] ist demnach irrational.
Berechnung des Wertes eines periodischen Kettenbruchs
Sei [math] \xi [/math] eine reelle Zahl gegeben durch [math] \: \xi := 4 + \dfrac{1}{1+\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{2+\dfrac{1}{\hspace{10pt} \ddots}}}}}}} [/math]
Um einen ungefähren Wert von [math] \xi [/math] zu berechnen, reicht es, den Wert eines Partialbruchs des Kettenbruchs zu bestimmen:
[math] \: \xi \approx 4 + \dfrac{1}{1+\dfrac{1}{2+\dfrac{1}{3}}} = \dfrac{47}{10} [/math]
Da dieser Kettenbruch aber periodisch ist, können wir auch den exakten Wert von [math] \xi [/math] berechnen[5]. Dazu definieren wir
[math] \theta := 2+\dfrac{1}{3+\dfrac{1}{2+\dfrac{1}{3+\dfrac{1}{2+\dfrac{1}{\hspace{10pt} \ddots}}}}} [/math]
Es gilt [math] \: \theta = 2 + \dfrac{1}{3 + \dfrac{1}{\theta}} = 2 + \dfrac{\theta}{3\theta + 1} \\ \\
\Rightarrow \theta^{2} - 2\theta - \dfrac{2}{3} = 0 \\ \\
\Rightarrow \theta = \dfrac{3 + \sqrt{15}}{3} [/math]
[math] \Rightarrow \xi = 4 + \dfrac{1}{1+\dfrac{1}{\theta}} = 4 + \dfrac{\theta}{1 + \theta} = 4 + \dfrac{3 + \sqrt{15}}{6 + \sqrt{15}} = 4 + \dfrac{1 + \sqrt{15}}{7} = \dfrac{29 + \sqrt{15}}{7} [/math]
Kettenbruchdarstellung von [math] \pi [/math]
[math] \pi[/math][6][math] = 3+\dfrac{1}{7+\dfrac{1}{15+\dfrac{1}{1+\dfrac{1}{292+\dfrac{1}{1+{\dfrac{1}{\hspace{10pt} \ddots}}}}}}} [/math]
Da wir den Wert von [math] \pi [/math] kennen, können wir es als regulären Kettenbruch entwickeln. Werten wir dessen Partialbrüche aus, sehen wir, dass sie eine gute Annäherung an [math] \pi [/math] liefern.
| [math] \begin{align} \pi &= 3.1415926535897932384626433832795028... \\ &= \left\lt 3;7,15,1,292,1,1,1,2,1,3,1,14,2,1,1,...\right\gt \end{align} [/math] | ||
|---|---|---|
| Partialbruch | ermittelter Bruch | Wert als Dezimalzahl |
| [math] \left\lt 3\right\gt [/math] | [math] \dfrac{3}{1} [/math] | 3.00000000000000... |
| [math]\left\lt 3;7\right\gt [/math] | [math]\dfrac{22}{7} [/math] | 3.14285714285714... |
| [math]\left\lt 3;7,15\right\gt [/math] | [math]\dfrac{333}{106} [/math] | 3.14150943396226... |
| [math]\left\lt 3;7,15,1\right\gt [/math] | [math]\dfrac{355}{113} [/math] | 3.14159292035398... |
| [math]\left\lt 3;7,15,1,292\right\gt [/math] | [math]\dfrac{103993}{33102} [/math] | 3.14159265301190... |
| [math]\left\lt 3;7,15,1,292,1\right\gt [/math] | [math]\dfrac{104348}{33215}[/math] | 3.14159265392142... |
| [math]\left\lt 3;7,15,1,292,1,1\right\gt [/math] | [math]\dfrac{208341}{66317} [/math] | 3.14159265346744... |
| [math]\left\lt 3;7,15,1,292,1,1,1\right\gt [/math] | [math]\dfrac{312689}{99532} [/math] | 3.14159265361894... |
| [math]\left\lt 3;7,15,1,292,1,1,1,2\right\gt [/math] | [math]\dfrac{833719}{265381} [/math] | 3.14159265358108... |
Da [math] \pi [/math] irrational ist und bisher keine Muster in dessen regulärem Kettenbruch gefunden wurden, können wir nur endliche Partialbrüche von diesem berechnen. Wenn wir uns aber nicht auf reguläre Kettenbrüche beschränken, gibt es Kettenbrüche von [math] \pi [/math], die Muster enthalten.[7]
So zeigte Johann Heinrich Lambert:
[math] \dfrac{4}{\pi}=1+\dfrac{1^2}{3+\dfrac{2^2}{5+\dfrac{3^2}{7+\dfrac{4^2}{9+\dfrac{5^2}{11+\dfrac{6^2}{\hspace{10pt} \ddots}}}}}} [/math]
Von Leonhard Euler stammt:
[math] \pi= 1+\dfrac{1^2}{6+\dfrac{3^2}{6+\dfrac{5^2}{6+\dfrac{7^2}{6+\dfrac{9^2}{6+\dfrac{11^2}{\hspace{10pt} \ddots}}}}}} [/math]
Siehe auch
Einzelnachweise
- ↑ Hochspringen nach: 1,0 1,1 Johannes Klee: Endliche Kettenbrüche (2019), Masterseminar WiSe 19/20 an der TU Dortmund
- ↑ Bild wurde selbst hergestellt
- ↑ Bild wurde selbst hergestellt
- ↑ Algorithmen für regelmäßige Kettenbrüche Stefan Scheel, Bachelorarbeit an der Universität Kassel (2005)
- ↑ Thomas Boecker: Periodische Kettenbrüche Seminar zur Algebra und Zahlentheorie, WiSe 19/20 an der TU Dortmund
- ↑ Continued Fraction Approximations to [math] \pi [/math] University of Illinois - Department of Mathematics
- ↑ Zur Arithmetik von Kettenbrüchen Philipp Stopp, Bachelorarbeit vorgelegt der Mathematisch-Naturwissenschaftlichen Fakultät der Universität des Saarlandes (2009)