Cantor-Menge

Georg Cantor - eine Vorstellung

Georg Ferdinand Ludwig Philipp Cantor (geboren am 3. März 1845 (nach dem gregorianischen Kalendar) in Sankt Petersburg und gestorben am 6. Januar 1918 in Halle an der Saale) war ein detuscher Mathematiker. Er war das Kind von dem Kaufmann und Börsenmakler Georg Woldemar Cantor und Marie Cantor.

Mathematischer Werdegang

Cantor schloss die Schule 1860 mit Auszeichnung an der Realschule Darmstadt ab. Nachdem besuchte er die Höhere Gewerbeschule Darmstadt, was heute die TU Darmstadt ist, wo er durch den Wille seines Vaters eine Berufsausbildung zum Ingenieur begann. Cantors Stärken aber lagen in der Mathematik und 1862 begann er ein Mathematikstudium am Polytechnikum in Zürich, wobei er 1863 an die Universität Berlin wechselte. 1866 studierte er ein Sommersemester in Göttingen und 1867 wurde er an der Universität Berlin bei Ernst Eduard Kummer promoviert. Zu seinen Lehrern zählen die bekannten Mathematiker Karl Weierstraß, Ernst Eduard Kummer und Leopold Kronecker. Nach seinem Studium arbeitete Cantor als Mathematiklehrer am Friedrich-Wilhelm Gymnasium in Berlin. Bereits dort litt er an Depressionen. 1869 habilitierte er an der Universität Halle, wo er, mit dem Thema De transformatione formarum ternarium quadricarum, bis zum Ende seines Lebens lehrte und arbeitete. Vorab arbeitete er dort als Privatdozent, seit 1872 als Extraordinarius und seit 1877 bis zu seinem Ruhestand 1913 als ordentlicher Professor.

Werk und Leben

Cantor ist der Begründer der Mengenlehre und prägte den Begriff der Unendlichkeit. Im Jahre 1870 gelang es ihm, eine Funktion als Summe trigonometrischer Reihen darzustellen. Ab 1872 veröffentlichte er weitere Arbeiten über trigonometrische Reihen. 1873 folgte der Beweis, dass die rationalen Zahlen abzählbar sind und somit eine Bijektion zwischen den natürlichen Zahlen und den rationalen Zahlen existiert. (1. Cantorsches Diagonalargument). 1874 zeigte er über das 2. Cantorsche Diagonalargument, dass die reellen Zahlen überabzählbar sind. 1877 beschäftigte er sich mit den geometrischen Anwendungen der Mengenlehre. Er ist beispielsweise von der Annahme ausgegangen, dass ein Quadrat der Seitenlänge 1 nicht genauso viele Elemente enthält, wie eine Linie zwischen 0 und 1. Als er herausfand, dass dem doch so ist, war er von seiner Entdeckung und Beweisführung überrascht. Er schrieb deshalb „Ich sehe es, aber ich glaube es nicht“. Seine neue Entdeckung hatte großen Einfluss auf die bisherigen geometrischen Anschauungen. Seine Abhandlungen zu dem Thema wurden von Leopold Kronecker, der dem Begriff der Unendlichkeit kritisch gegenüberstand, zurückgehalten und erst die Intervention seines Freundes Dedekind führten zur Veröffentlichung. Von 1879 bis 1884 gab er die Artikelreihe mit dem Namen „Über unendliche lineare Punktmannigfaltigkeiten“ heraus, in der er die Grundlagen und Hauptsätze der Mengenlehre begründete. Seine Erkenntnisse führten zu großem Widerstand, weshalb er fast zehn Jahre lang sein Fachgebiet wechselte und sich vermehrt den Literaturwissenschaften, der Philosophie und der Theologie zuwandt. Seine zweite Lebenshälfte wurde vermehrt von seiner manisch-depressiven Erkrankung geprägt, weshalb er sich in psychiatrische Behandlung begeben musste. Erst 1895 wandte er sich wieder seinem ursprünglichen Gebiet, der Mengenlehre, zu, nachdem er zunehmend Anerkennung und Wertschätzung für seine Arbeit erhielt. 1899 musste er sich erneut einem Sanatoriumsaufenthalt unterziehen. Kurz nach dem Aufenthalt verstarb sein jüngster Sohn, weshalb sich Cantors psychische Erkrankung verschlimmerte und ein weiterer Sanatoriumsaufenthalt 1903 folgte. Unter seinen Depressionen litt folglich seine mathematische Arbeit. 1913 ging er in Pension. Kurz darauf begann 1914 der erste Weltkrieg. Während diesem litt er an Armut und Mangelernährung. Am 6. Januar 1918 starb Cantor an einer Herzinsuffizienz in dem Sanatorium in Halle, in welchem er sein letztes Lebensjahr verbrachte.

Vgl. : https://de.wikipedia.org/wiki/Georg_Cantor

Geometrische Darstellung

Man konstruiert die Cantor-Menge C rekursiv, indem man vom abgeschlossenen Intervall [0, 1] das mittlere offene Drittel [math]\displaystyle ( \frac{1}{3} ,\frac{2}{3} )[/math] entfernt und aus den beiden verbleibenden Intervallen [[math]\displaystyle\ 0[/math], \frac{1}{3} </math>] [0, 1/3] und [[math]\displaystyle\frac{2}{3} , 1[/math]] erneut jeweils deren mittleres offenes Drittel entfernt. Dieser Prozess des Entfernen des mittleren offenen Drittels wird unendlich oft fortgesetzt.

Folgendes Bild veranschaulicht den Prozess.

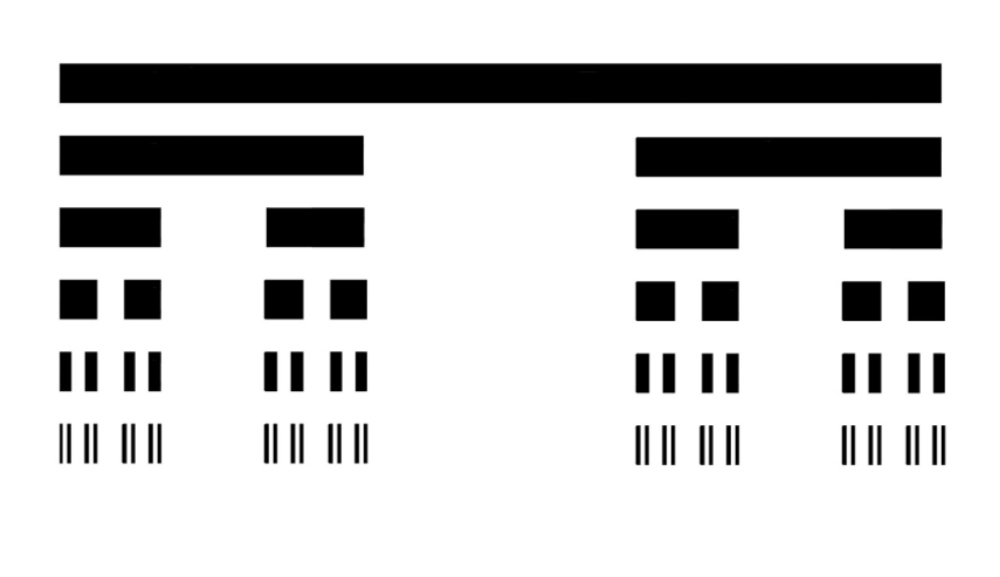
Tenär-Darstellung

Der internationale Standard sieht das Dezimalsystem als Zahlensystem vor. Dabei wird ein Zahlenwert dargestellt durch Ziffern 0,1,2,3,4,5,6,7,8,9 mit dem Stellenwert als Zehnerpotenz insgesamt addiert wird. Da bei der Cantor-Menge Intervalle iterativ gedrittelt werden, ist es zielführend sich für die nähere Betrachtung der Menge mit dem Stellenwertsystem zur Basis 3 vertraut zu machen, dem Tenär-System. Dieses sieht die Ziffern 0,1,2 und den Stellenwert als Dreierpotenz vor. Zahlenwerte in Tenär-Darstellung werden mit einem Index 3 gekennzeichnet. Das heißt für x ∈ [0, 1], dem Intervall in dem sich die Cantor-Menge befindet, im:

• Dezimalsystem:
  

[math]\displaystyle x = 0,x_1 x_2 x_3 ... = \sum_{i=1}^\infty x_i \frac{1}{10^i} ; x_i ∈ [/math] {0,1,...,9} ,wobei i ∈ [math]\mathbb N[/math]

• Tenärsystem:
  

[math]\displaystyle x = 0,x_1 x_2 x_3 ...= \sum_{i=1}^\infty x_i \frac{1}{3^i} ; x_i ∈ [/math] {0,1,2} ,wobei i ∈ [math]\mathbb N[/math]

Beispiele dazu:

[math]\displaystyle \frac{1}{3} = (0,1)_3 [/math]

[math]\displaystyle \frac{2}{3} = \frac{1}{3} + \frac{1}{3} = (0,2)_3 [/math]

[math]\displaystyle \frac{13}{27} = \frac{1}{3}+\frac{1}{9}+\frac{1}{27}= \frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3} = (0,111)_3 [/math]

So wie im Dezimalsystem die Konvention besteht [math]\displaystyle 0{,}\overline{9}[/math] mit 1 gleichzusetzten, gilt dies analog für [math]\displaystyle 0{,}\overline{2}[/math] im Tenärsystem. Daraus folgt:

[math]\displaystyle (0{,}\overline{2})_3 = 1[/math]

[math]\displaystyle(0{,}0\overline{2})_3 =(0,1)_3[/math]

[math]\displaystyle(0{,}11\overline{2})_3 =(0,12)_3[/math]

Angewandt auf die Cantor-Menge bedeutet das, da das mittlere Intervall mit einer 1 als Stellenwert herausgenommen wird, dass die Menge C_n aus Elementen besteht, die innerhalb denr ersten n-Nachkommstellen nur aus den Ziffern 0 und 2 bestehen. Das erleichtert die Zuordnug. Deswegen

[math]\displaystyle C_n = [/math]{<math>\displaystyle c ∈ }

Cantorfunktion

Mit Hilfe der Cantormenge C lässt sich rekursiv die sogenannte Cantorfunktion (auch “Teufelstreppe”) definieren. Sei f: [0,1] -> [0,1] mit f(0) = 0 und f(1) = 1. Sei x in [0,1], dann erhalten wir die Cantorfunktion f(x) durch die folgenden Schritte:

• Drücke x in Basis 3 approximiert aus
• Wenn x eine 1 enthält, ersetze jede Ziffer streng nach der ersten 1 durch 0.
• Ersetze alle verbleibenden 2en durch 1en.
• Interpretiere das Ergebnis als Binärzahl.

Der Graph der Funktion ist durch folgendes Bild veranschaulicht.

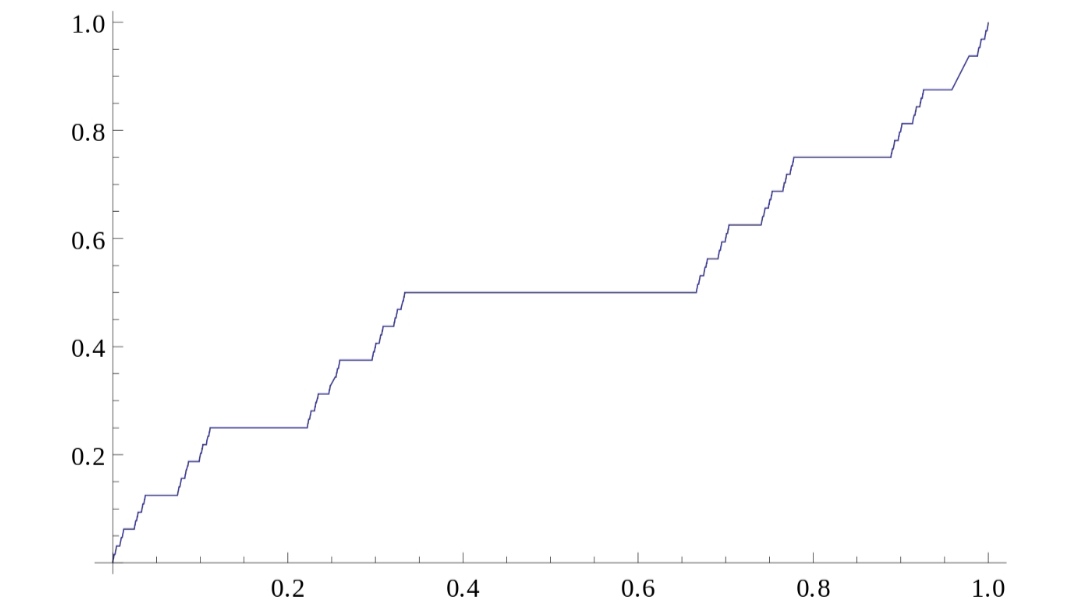
Die Teufelstreppe f ist monoton steigend und in allen Punkten x  ∈  [0, 1] \ C differenzierbar mit der Ableitung 0, da sie dort konstant ist. In den Elementen der Cantormenge wie zum Beispiel 0 und 1 und den Randpunkten der entfernten Drittelintervalle ist f nicht differenzierbar.

Sie steht in Bezug mit einer besonderen Wahrscheinlichkeitsverteilung.

Eigenschaften

1884 veröffentlicht Cantor sein Werk Über unendliche, lineare Punktmannigfaltigkeiten (VI). Im Paragraph § 19 beschäftigt er sich mit perfekten Teilmengen von ℝ. Hierzu verwendet er die Cantormenge und zeigt, dass jede beschränkte nichtleere perfekte Teilmenge von ℝ, die keine nichttrivialen Intervalle enthält, ähnlich ist zur Cantormenge C.

In der Tat hat die Cantormenge C besondere Eigenschaften:

• C ist kompakt.
• C hat keine isolierte Punkte.
• C Lange TITEL ZU ANDERN
• C ist total unzusammenhängend und hat ein leeres Inneres.
• C ist überabzählbar.

Kompaktheit

Da die Cantor-Menge eine Teilmenge der Reelen Zahlen ist, gilt der Satz von Heine-Borel, dass Mengen genau dann kompakt sind, wenn sie abgeschlossen und beschränkt sind. Abgeschlossenheit der Cantor-Menge C [math]\Leftrightarrow offenes Komplement \lt math\gt \mathbb R [/math] \C

[math]\mathbb R [/math] \C =   [math]\mathbb R [/math] \ [0, 1]

Perfektheit

Sei M ein topologischer Raum, eine Teilmenge A ⊂ M heißt perfekt, wenn A kompakt ist und keine isolierte Punkte hat. Ein Punkt pheißt isoliert, falls es eine Umgebung um p gibt, die p als einziger Punkt enthält.

Wie schon erwähnt, ist die Cantormenge eine solche Menge (Vgl: C total unzusammenhängend).

Länge

Es gilt, dass die Menge C_n aus 2ⁿ Intervallen der Länge 1/3ⁿ besteht. Folglich ist die Gesamtlänge von C_n |C_n| = 2ⁿ * 1/3ⁿ = (2/3)ⁿ. Um also die Gesamtlänge |C| der Cantor-Menge zu erhalten, betrachtet man nun den Limes: lim_n→∞ ((2/3)ⁿ). Da (2/3)ⁿ bekanntlich eine Nullfolge ist, folgt also: |C| = 0, womit die Länge der Cantormenge 0 ist.

Inneres

Das Innere von C ist leer: C° = ∅.

Beweis per Widerspruch:

Annahme, es gebe ein x ∈ das Innere von C (C’). Dann gibt es ein ε > 0 mit (x−ε,x+ε) ⊂ C‘ ⊂ C. Dann gilt auch für alle n ∈ N, dass (x−ε,x+ε) ⊂ Cn. Die Gesamtlänge von Cn erfüllt also 2ε ≤ (Summenzeichen)2n, k=1 |In,k | = 2^n /3^n=(2/3)^n . Dies widerspricht jedoch der oben genannten bewiesenen Konvergenz, welche 0 ist.

TOTAL UNZUSAEMMENH. TITEL ZU AENDERN

//ganz am Ende des Paragraphs oder wo ihr denkt, vielleicht: // Deswegen ist C auch Cantorsches Diskontinuum genannt.

Kardinalität

Durch das 2. Cantorsches Diagonalverfahren kann mann beweisen, dass die Cantomenge überabzählbar ist.

Folgendes Bild veranschaulicht das Verfahren.

Musikalische Interpretation

Der rumänische Komponist György Ligeti macht in seiner Komposition "L'escalier du diable" (“Die Teufelstreppe”) innerhalb seiner 13. Etüde die Cantor-Funktion musikalisch fühlbar.

Der endliche Aufstieg des Intervalls [0, 1] in überabzählbar unendlich vielen Schritten ist durch sich selbstähnlich Harmonien illustriert. Die konstanten Abschnitte der Cantor-Funktion, aufgrund der herausgenommen Intervall, sind in Ligetis Werk erkennbar. Die steigende Monotonie der Funktion wird durch ein sich beschleunigendes Tempo in der Komposition ausgedrückt. Ihre Struktur ist dreiteilig. Nach dem ersten musikalischen Intervall wird der mittlere Teil des nächsten Intervall verändert und dann nochmals mit einem veränderten mittleren geteilt.

Die Komposition versucht eine Darstellung der Unendlichkeit in der Kunst zu geben, was in der Mathematik formal möglich ist. Siehe

Quellen und weiterführende Links

https://wiki.math.ntnu.no/_media/tma4225/2015h/cantor_set_function.pdf (letzter Zugriff 30.03.2021)