Primzahlen: Unterschied zwischen den Versionen
K |
|||
| Zeile 144: | Zeile 144: | ||
<pre> | <pre> | ||
#include <iostream> | #include <iostream> | ||
| + | #include <cmath> | ||
int main(int argc, const char** argv) { | int main(int argc, const char** argv) { | ||
| + | // erstelle eine Liste der Laenge N. Zu Beginn sind keine Zahlen gestrichen was durch 'false' dargestellt wird | ||
const unsigned int N = 100; | const unsigned int N = 100; | ||
bool Liste[N] = { false }; | bool Liste[N] = { false }; | ||
| − | // iteriere über alle Zahlen in der Liste | + | // iteriere über alle Zahlen in der Liste bis zur Wurzel von N |
| − | for (int i = 2; i <= N; i++) { | + | for (int i = 2; i <= std::sqrt(N); i++) { |
// falls Index noch nicht gestrichen sind | // falls Index noch nicht gestrichen sind | ||
Version vom 31. März 2021, 20:40 Uhr
Definition
Sei [math] p \in \mathbb{N} [/math]. Hat p genau zwei Teiler so wird p Primzahl genannt. Wir bezeichnen [math]\mathbb P[/math] als die Menge aller Primzahlen.
Arten von Primzahlen
Primzahlen werden aufgrund ihrer zahlentheoretischen Eigenschaften in verschiedene Kategorien zuammengefasst.
Primzahltupel
Jedes Paar [math]( p_1 , p_2 ) [/math]aus zwei Primzahlen [math]p_1[/math] und [math]p_2[/math] mit der Differenz 2 wird Primzahlzwilling genannt. Sie haben also die Form [math](p_1,p_1+2[/math]). Ein paar aus drei Primzahlen, die den Abstand von 2 haben wird hingegen als Primzahldrilling bezeichnet und hat die Form [math](p,p+2,p+4)[/math]. Nur das Paar [math](3,5,7)[/math] ist ein Primzahldrilling, da unter drei aufeinanderfolgenden ungerade Zahlen stets eine durch 3 teilbar ist. Diese Definition lässt sich auf Primzahltupel erweitern, die weitere Bezeichnungen einschließt wie Primzahlvierlinge oder Primzahlcousins. Insbesondere auch die Paare mit Abstand 6 die als sexy Primzahlen bezeichent werden.
Mersennesche Primzahlen
Ist [math] p \in \mathbb{P}[/math] und hat die Form [math]2^{n}-1 [/math] für [math]n \in \mathbb{P} [/math] so wird [math]p[/math] als Mersennesche Primzahl bezeichnet. Der Name geht auf den französischen Theologen und Mathematiker Marin Mersenne (8.8.1588 bis 1.8.1648) zurück.
Wobei zu beachten ist, dass [math] n \in \mathbb{P} [/math] wieder eine Primzahl ist und dass nicht alle Zahlen der Form [math] 2^{p}-1 [/math] Primzahlen sind. Ein konkretes Beispiel für einen solchen Fall ist die Zahl [math]2^{11}-1 = 2047[/math], welche sich auch als [math] 23*89 [/math] darstellen lässt und somit keine Primzahl ist.
Mersenne Primzahlen lassen sich im Binärsystem als Folge von Einsen schreiben. So hat Beispielsweise [math] 2^{19}-1 = 524.287 [/math] im Binärsystem die Form [math] 1111111111111111111_2 [/math] Gegenwärtig sind viele der größten bekannten Primzahlen Mersenne-Primzahlen, da durch den Lucas-Lehmer Test Zahlen der Form [math]2^{n}-1[/math] verhältnismäßig effizient auf die Primzahleigenschaft überprüfen lassen.
Sophie-Germain Primzahlen
Gilt für eine Primzahl [math]p[/math], dass auch [math]2p+1[/math] eine Primzahl ist, so wird [math]p[/math] Sophie-Germain Primzahl genannt und [math]2p+1[/math] sichere Primzahl
Fermat Primzahlen
Primzahlen der folgenden Form werden Fermat Primzahlen genannt.
- [math] p = 2^{2^n} + 1[/math]
mit einer ganzen Zahl [math]n \ge 0[/math]
Ramanujan Primzahl
Ramanujan-Primzahlen [math]R_n[/math] sind als kleinste Zahlen definiert, so dass für alle [math]x \geq R_n[/math] zwischen [math] x[/math] und [math]\tfrac {x}{2}[/math] mindestens [math]n[/math] Primzahlen liegen
Größte berechnete Primzahl
| Zahl | Anzahl der Dezimalziffern |
Jahr | Entdecker (genutzter Computer) |
|---|---|---|---|
| 282.589.933−1 | 24.862.048 | 2018 | Patrick Laroche et al. (GIMPS, Intel i5-4590T @ 2.0 GHz[1]) |
Satz von Euklid
Im Jahr 300 v.u.Z hat Euklid von Alexandria bewiesen, dass es unendlich viele Primzahlen gibt.
In seinem Beweis durch Widerspruch trifft er die Annahme, dass es nur endlich viele Primzahlen gibt. Danach definiert er eine neue Zahl die eine neue Primzahl als Teiler hat oder welche selbst Primzahl ist. Somit erhälten wir einen Widerspruch und es kann keine endliche Menge aller Primzahlen geben. Es wurden mittlerweile dutzende weitere Beweise veröffentlicht[2].
Primzahlsatz
Ein wichtiger Teil der Arbeiten zu Primzahlen beschäftigt sich mit der Verteilung dieser. Hierfür wird die Primzahlfunktion definiert die uns die Anzahl der Primzahlen an gegebener Stelle wiedergibt und versuchen dann genaue Eigenschaften dieser Funktion festzuhalten.
Die Primzahlfunktion
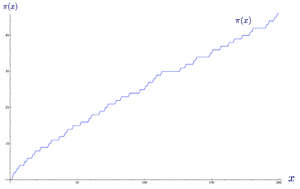
Diese Funktion ist für beliebige [math]x \in R [/math] definiert und gibt die Anzahl der Primzahlen an, die nicht größer als [math]x[/math] sind.
- [math]\pi (x) := \left | \{p \in \mathbb{P} \mid p \le x\} \right |[/math]
[math]\pi(x)[/math] wird als Primzahlfunktion bezeichnet.
| Die Primzahlfunktion:
In der Graphik ist die Treppenfunktion bis zu einem Wert von 200 zu sehen. |
Diese Funktion ist auch ein zentrales Untersuchungsobjekt für Bertrand Riemann in seiner Arbeit Über die Anzahl der Primzahlen unter einer gegebenen Größe in der er die Riemannsche Vermutung formuliert.
Der Primzahlsatz
Die Urfassung des Primzahlsatzes geht auf Gauß zurück, welchen er im Alter von 15 Jahren, im Jahre 1792 formuliert.
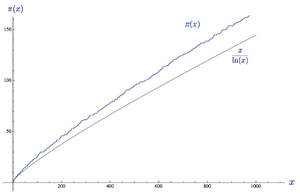
Sei [math]\displaystyle \mathrm{Li}(x):=\int _{2}^{x}{\frac { \mathrm{d}t }{\ln {t}} } [/math] der Integrallogarithmus. Dann gilt [math]\displaystyle \lim _{{x\to \infty }}{\frac {\pi (x)}{\mathrm{Li(x)}}}=1 [/math]
Diese Eigenschaft wird als asymptotisch äquivalent bezeichnet und schreibe
- [math]\displaystyle \pi (x) \sim \mathrm{Li(x)} [/math]
Es kann gezeigt werden, dass gilt:
- [math]\displaystyle Li(x) \sim \frac {x}{\ln(x)} [/math]
So formulieren wir den Primzahl, wie er in den meisten Werken zu finden ist.
- [math]\displaystyle \pi (x) \sim \frac{x}{\ln {x}} [/math]
| Primzahlfunktion und Integrallogarithmusfunktion:
Der Verlauf der Funktionen ist bis zum Wert 200 abgebildet. | |
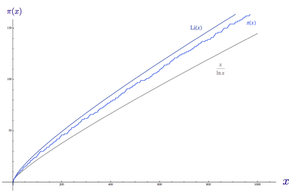
| Primzahlfunktion, Integrallogarithmusfunktion und x/log(x):
Alle drei Funktionen sind im Verlauf bis 200 abgebildet. Die Primzahlfunktion scheint hierbei von den anderen beiden Funktionen eingeschnürrt zuwerden. Die Integrallogarithmusfunktion scheint insbesondere die Primzahlfuntion immer zu überschätzt. Der Mathematiker John Littlewood bewies aber 1913, dass [math] Li(x) [/math] an einem bestimmten Wert x die Primzahlfunktion unterschreiten muss. Stanley Skewes konnte zeigen, dass dies unter dem Wert [math]10^{10^{10^{34}}}[/math] passieren muss. Diese Zahl ist als Skewes-Zahl bekannt. |
Der Mathematiker Hans von Mangoldt konnte im Jahre 1895 beweisen, dass der Primzahlsatz äquivalent dazu ist, dass die Riemannsche Zeta-Funktion keine Nullstellen hat bei Funktionswerten mit Realteil 1.
Primfaktorzerlegung
Es ist möglich jede natürliche Zahl eindeutig als Produkt von sogenannten Primfaktoren darzustellen.
Definition
- Eine Zahl [math] p [/math] heißt <it> Primfaktor </it> einer natürlichen Zahl [math] n [/math], wenn
- [math] p [/math] [math] n [/math] ganzzahlig ohne Rest teilt und
- [math] p [/math] eine Primzahl ist.
- Die Darstellung einer natürlichen Zahl [math] n [/math] als Produkt ihrer Primfaktoren nennt man Primfaktorzerlegung.
Eigenschaften
- Eine Primfaktorzerlegung ist bis auf die Reihenfolge der Primfaktoren eindeutig.
- Da 1 keine Primzahl ist, ist die Primfaktorlzerlegung von 1 ein leeres Produkt
- Der gleiche Primfaktor kann mehrmals in einer Primfaktorzerlegung vorkommen
- Es gibt kein effizientes Verfahren, die Primfaktorzerlegung einer Zahl zu bestimmen
- Für Zahlen mit sehr großen Primfaktoren ist es ein enormer Aufwand die Primfaktorzerlegung zu bestimmen
- Wählt man die Primfaktoren groß genug, so benötigen sogar Hochleistungsrechner mehrere Jahre, um die Primfaktorzerlegung zu bestimmen.
Beispiele
\[ 6 = 2 * 3 \] \[ 7 = 7 \] \[ 1003 = 17 * 59 \] \[ 94684 = 2 * 2 * 23671 \]
Anwendungen
Primzahlen in der Natur
Es existieren Zikadenarten, die sich in einem festen Abstand von Jahren massenhaft über der Erde vermehren und danach wieder unter die Erde zurückkehren. In dieser Zeit sind sie weniger gut vor ihren Fressfeinden geschützt. Die Zikaden haben also einen Vorteil, wenn sie in Jahren über der Erde sind, in denen weniger Fressfeinde auftreten. Einige Zikadenarten nutzen genau diesen Vorteil: Sie vermehren sich im Abstand von 13 oder 17 Jahren über der Erde.
Was passiert also mit ihren Fressfeinden? Für solche, die ohnehin in jedem Jahr auftreten, ändert sich nichts. Allerdings gibt es auch solche, die selbst nur in gewissen Jahren auftreten. Beispielsweise existiert eine zikadenjagende Wespe, die alle zwei bis drei Jahre auftritt. Nehmen wir also eine Art an, die alle 2 Jahre auftritt. Würden sich die Zikaden alle 12 Jahre vermehren, so würde in jedem dieser Jahre auch die Wespenart auftreten und die Zikaden hätten es mit deutlich mehr Fressfeinden zu tun. Nun ist der Zyklus der Zikaden aber 13 Jahre lang. Sie müssen also nur alle 26 Jahre mit jener Wespenart fertig werden. Somit haben sie einen deutlichen Vorteil darin, sich zu vermehren[3].
Primzahltests
Sieb des Eratosthenes
Das Sieb des Eratosthenes ist eines der ältesten Verfahren zur Bestimmung aller Primzahlen, bis hin zu einer frei wählbaren oberen Grenze. Das Verfahren ist nach dem griechischen Mathematiker Eratosthenes von Kyrene (ca. 276 v.Chr. bis ca. 194 v.Chr) benannt. Konzeptionell arbeitet das Verfahren auf Liste von Zahlen, beginnend mit der 2 bis hin zu der oberen Grenze N. Anschließend werden nacheinander alle Zahlen in dieser Liste betrachtet. Ist die betrachtete Zahl nicht markiert, so ist sie eine Primzahl und alle ihre Vielfachen können gestrichen werden. Ist die Zahl bereits markiert, kann man zur nächsten weitergehen. So werden nacheinander alle Primzahlen aus der Liste "herausgesiebt".
Ablauf des Algorithmus
- Wähle eine obere Grenze N, bis zu der alle Primzahlen bestimmt werden sollen.
- Schreibe alle natürlichen Zahlen von 2 bis N auf (um das Ganze anschaulicher zu machen ordnet man die Zahlen meist in einem rechteckigen Schema an, wobei hier die Vielfachen von 10 am Ender einer Reihe stehen). Im Folgenden werden alle Zahlen die keine Primzahlen sind gestrichen.
- Begonnen wird mit der 2. Die 2 selbst ist eine Primzahl, es können aber alle Vielfachen von 2 gestrichen werden, da sie selbst keine Primzahlen sind.
- Die nächste nicht gestrichene Zahl ist die Primzahl 3. Wieder können alle Vielfachen von 3 gestrichen werden. Begonnen werden kann hier mit der Quadratzahl von 3 (9) (warum?)
- Die 4 wurde bereits im 2. Schritt gestrichen und die nächste Zahl kann betrachtet werden.
- Dieses Vorgehen wird mit allen folgenden Zahlen wiederholt. Ist eine Zahl noch nicht gestrichen worden, wenn man sie betrachtet, so ist sie eine Primzahl und ihre Vielfachen können gestrichen werden. Andernfalls kann die nächste Zahl betrachtet werden.
- Der Vorgang wird wiederholt, bis man bei der oberen Grenze N angelangt ist.
Der Algorithmus selbst ist recht Intuitiv und leicht nach zu vollziehen. Auch erklärt sich durch den Algorithmus, wie der Name "_Sieb_ des Eratosthenes" zu stande kommt.
Bemerkung: Spielt man den Algorithmus durch, kann man schnell erkennen, dass beim Streichen von Kandidaten, viele Zahlen mehrfach gestrichen werden. (TODO: Beispiel) Dabei handelt es sich letztlich um überflüssige Operationen.
#include <iostream>
#include <cmath>
int main(int argc, const char** argv) {
// erstelle eine Liste der Laenge N. Zu Beginn sind keine Zahlen gestrichen was durch 'false' dargestellt wird
const unsigned int N = 100;
bool Liste[N] = { false };
// iteriere über alle Zahlen in der Liste bis zur Wurzel von N
for (int i = 2; i <= std::sqrt(N); i++) {
// falls Index noch nicht gestrichen sind
if (Liste[i] == false) {
// streiche alle Vielfachen beginnend mit dem Quadrat der gegenwärtig betrachteten Zahl an der Stelle i
for (int j = i*i; j < N; j += i) {
Liste[j] = true;
}
}
}
// gebe alle Primzahlen aus
for (int i = 2; i <= N; i++){
if (Liste[i] == false){
std::cout << i << std::endl;
}
}
return 0;
}
Lucas-Lehmer Test
Der Lucas-Lehmer-Test ist ein Verfahren um zu überprüfen, ob es sich bei einer gegebenen Mersenne-Zahl auch um eine Mersenne-Primzahl handelt. Der Test geht auf den französischen Mathematiker François Édouard Anatole Lucas(*4.4.1842 † 3.10.1891) zurück wurde aber erst 1930 von dem US-Amerikanischen Mathematiker Derrick Henry Lehmer (* 23.2.1905 † 22.5.1991) entwickelt.
Primzahlen in der Kryptographie
Die Tatsache, dass es bis heute keine effiziente Methode zum Zerlegen einer großen Zahl in ihre Primfaktoren gibt, ermöglicht einige Anwendungen in der Kryptographie. So verwenden einige Verfahren, die eine verschlüsselte Kommunikation gewährleisten, Primzahlen. Wie wichtig solche Verfahren sind, wird deutlich, wenn man sich ansieht, wobei diese benutzt werden. Das umfasst Anwendungen wie Emails, Chats und Internettelefonie, aber auch weitaus sensiblere Daten, wie beispielsweise beim Onlinebanking.
RSA-Verfahren
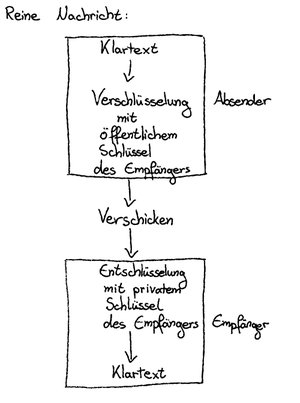
Das RSA-Verfahren wurde 1978 von Ron Rivest, Adi Shamir und Leonard Adleman vorgestellt und nach ihnen benannt. Es ist ein public-key Krytosystem, nutzt also ein Schlüsselpaar, das aus einem öffentlichen und einem privaten Schlüssel besteht. Dies hat den Vorteil, dass der öffentlichen Schlüssel nicht geheim weitergegeben werden muss und so der Schlüsselaustausch kein Sicherheitsrisiko darstellt.
Public-key System
Bei einem Public-key System besitzt jeder Anwender sein eigenes Schlüsselpaar aus privatem und öffentlichen Schlüssel und somit auch sein eigenes Ver- und Entschlüsselungsverfahren. Dabei wird der geheime Schlüssel vom Anwender geheimgehalten, während der öffentliche Schlüssel an alle anderen Anwender, mit denen kommuniziert wird, verteilt wird.
Der Verschlüsselungsprozess wird mit [math] D [/math] bezeichnet, der Entschlüsselungsprozess mit [math] E [/math]. Ein Schlüsselpaar besteht aus zwei Zahlen. Dabei gelten für eine Nachricht im Klartext M die folgenden Eigenschaften:
- [math] D(E(M)) = M [/math]
- [math] E(D(M)) = M [/math]
- E und D sind für sich genommen leicht zu berechnen
- E kann aus D nicht einfach berechnet werden
Ein Entschlüsselungsprozess [math] E [/math] heißt trap-door one-way function, wenn er die Eigenschaften a, c und d erfüllt. Handelt es sich außerdem um einen Prozess, der b erfüllt, so wird daraus eine trap-door one-way permutation. Dann ist jeder Geheimtext eine potenzielle Nachricht und jede Nachricht ein potenzieller Geheimtext.
Betrachten wir nun das Konzept des RSA-Verfahrens an einem Beispiel. Im Folgenden möchte Felix Ari eine Nachricht schicken. Dementsprechend besitzt Felix die Schlüsselverfahren [math] D_F [/math] und [math] E_F [/math], Ari entsprechend [math] D_A [/math] und [math] E_A [/math].
Wie sieht nun der Nachrichtenaustausch aus? Zuallererst müssen Felix und Ari ihre öffentlichen Schlüssel austauschen. Somit erhält Ari die Möglichkeit [math] E_F [/math] durchzuführen, Felix [math] E_A [/math].
Nun führt Felix auf seiner Nachricht [math] E_A [/math] aus. Er nutzt also den öffentlichen Schlüssel von Ari und versendet dann die Nachricht. Bekommt Ari nun die verschlüsselte Nachricht, so kann er sie mit [math] D_A [/math] entschlüsseln. Da nur er seinen privaten Schlüssel hat, kann auch niemand anderes die Nachricht entschlüsseln und lesen. Für die Antwort nutzt Ari dann [math] E_F [/math] für die Verschlüsselung.
Die Mathematik dahinter
Die Nachricht
Die Nachricht M selbst wird als positive ganze Zahl zwischen 0 und [math] n-1 [/math] kodiert, damit man leicht mit ihr rechnen kann. Wie groß [math] n [/math] ist, hängt vom einzelnen Schlüsselpaar ab. Ist die Nachricht zu groß, so wird sie in einzelne Blöcke aufgeteilt und jeder Block einzeln betrachtet. Eine mögliche Umwandlung von Buchstaben in Zahlen ist beispielsweise das ASCII-Format (hier Link einfügen).
Die Schlüsselpaare
Jeder der beiden Schlüssel besteht aus einem Tupel. \[ E = (e,n) \hspace{2cm} D = (d,n) \text{ wobei e, d, n positive ganze Zahlen sind.} \] Dabei gilt für den Ver- und Entschlüsselungsprozess eines Klartextes M und eines Geheimtextes C
- [math] C \equiv E(M) \equiv M^e \text{ mod } n [/math]
- [math] M \equiv D(C) \equiv C^d \text{ mod } n [/math]
Der Verschlüsselungsschlüssel an sich
- Zwei zufällige große Primzahlen [math][/math]</nowiki> und [math] q [/math] auswählen. Diese sollten in der Realität mehrere hundert Stellen haben.
- [math] n = p * q [/math]
- Weil [math] p [/math] und [math] q [/math] so groß sind, ist es nicht in realistischem Zeitaufwand möglich, aus [math] n [/math] [math] p [/math] und [math] q [/math] zu berechnen.
- Eine zufällige ganze Zahl d wählen, die folgende Bedingung erfüllt
- ggT([math]d, (q-1) * (p-1)) = 1[/math]
- ggT bezeichnet dabei den größten gemeinsamen Teiler (Hier Link einfügen)
- [math]d[/math] und [math] (q-1) * (p-1)[/math] müssen also teilerfremd sein
- e aus d bestimmen
\[ e * d = 1 (\text{ mod } \varphi(n)) \] (Hier Aussehen testen)
- [math] \varphi(n)[/math] bezeichnet die Eulersche [math] \varphi[/math]-Funktion (Hier Link einfügen)
Warum funktioniert das?
Nun gilt noch zu beweisen, dass dieses Verfahren für (fast) alle Nachrichten [math] M [/math] funktioniert.
Zuerst betrachten wir [math] \varphi(n) [/math]. Da für eine beliebige Primzahl [math] m [/math] gilt: \[ \varphi(m) = m-1 \] folgt für [math] n [/math] : \[ \varphi(n) = \varphi(p * q) \] \[ = (p-1) * (q-1) \] \[ = n - (p+q) + 1 \]
Wie hängt nun [math] \varphi(n) [/math] mit [math] e [/math] und [math] d [/math] zusammen?
Da [math] d [/math] teilerfremd zu [math] \varphi(n) [/math] ist, existiert ein multiplikatives Inverses [math] e [/math] im Ring [math] \mathbb{Z}/\varphi(n)\mathbb{Z} [/math]:
\[ e * d \equiv 1 (mod \ \varphi(n)) \]
Bisher gilt für den Ver- und Entschlüsselungsprozess \[ D(E(M)) \equiv (E(M))^d \equiv (M^e)^d \ (\text{mod} \ n) = M ^(e*d) \ (\text{mod }n \] und analog \[ E(D(M)) \equiv (D(M))^e \equiv (M^d)^e \ (\text{mod} \ n) = M ^(e*d) \ (\text{mod }n \]
Außerdem existiert eine ganze Zahl [math] k [/math], für die gilt: \[ M^{e*d} \equiv M^{k*\varphi(n) + 1} \ (\text{mod }n) \]
Nun gilt es noch zu zeigen, dass für alle [math] M [/math] gilt: [math] M^{e*d} = M \ (\text{mod }n) [/math]
Hierzu werden [math] p [/math] und [math] q [/math] getrennt betrachtet. Dies ist nach dem chinesischen Restsatz möglich, auf den wir hier nicht näher eingehen werden.
Betrachten wir [math] M^{e*d} = M \ (\text{mod }p) [/math], so gilt:
- Falls [math] M = 0 (\text{mod }p)[/math], dann ist [math] M [/math] ein Vielfaches von [math] p [/math]. Dann gilt: [math] M^{e*d} = 0 = M \ (\text{mod }p) [/math]
- Falls [math] M \not = 0 (\text{mod }p)[/math], dann gilt nach dem Satz von Euler-Fermat (Link)
[math] M^{ed} = M^{ed-1} M = M^{k(p-1)}M = (M^{p-1})^kM = 1^kM = M (\text{mod } p) \]
Betrachten wir \lt math\gt M^{e*d} = M \ (\text{mod }q) [/math], so gilt analog:
- Falls [math] M = 0 (\text{mod }q)[/math], dann ist [math] M [/math] ein Vielfaches von [math] q [/math]. Dann gilt: [math] M^{e*d} = 0 = M \ (\text{mod }q) [/math]
- Falls [math] M \not = 0 (\text{mod }q)[/math], dann gilt nach dem Satz von Euler-Fermat (Link)
[math] M^{ed} = M^{ed-1} M = M^{k(q-1)}M = (M^{q-1})^kM = 1^kM = M (\text{mod } q) \] \lt br\gt Da die Bedingung für beide Faktoren gezeigt wurde, gilt \lt math\gt M^{e*d} = M \ (\text{mod }n) [/math] nach dem chinesischen Restsatz auch für [math] n = pq [/math].
Einfaches Beispiel
Teil 1: Schlüssel generieren
- Wir wählen zwei Primzahlen [math] p = 7, \ q = 11 [/math]
- Dann gilt [math] n = pq = 77 [/math]
- Wir wählen ein e ganze Zahl [math] e = 29 [/math], wobei [math] p-1 = 6 [/math] und [math] q-1 = 10 [/math] teilerfremd zu [math] e [/math] sind.
- Der öffentliche Schlüssel ist dann [math] (e,N) = (29, 77)[/math]
- [math] \varphi(77) = (p-1) (q-1) = 6 * 10 = 60 [/math]
- Für [math] d [/math] gilt: [math] ed + k * \varphi(N) = 1, also \lt math\gt 29*d + k *60 = 1 [/math]. Somit ist [math] d=29 [/math] und der private Schlüssel [math] (d,N) = (29,77)[/math].
Wählt man deutlich größere Primzahlen [math] p [/math] und [math] q [/math], so ist die Berechnung von [math] e [/math] aus [math] d [/math] oder andersherum ohne die Kenntnis von [math] p [/math] und [math] q [/math] sogar für Computer zu aufwendig.
Teil 2: Die Verschlüsselung
Felix möchte die Zahl 13 verschlüsseln und an Ari senden. Hierzu rechnet er: \[ C = 13^{29}\ (\text{mod } 77) = 6 \] Diese 6 schickt Felix nun als Geheimtext an Ari.
Teil 3: Die Entschlüsselung
Ari rechnet nun: \[ M = 6^{29}\ (\text{mod } 77) = 13 \]
Und erhält somit wieder die 13 als Klartext.
Signatures
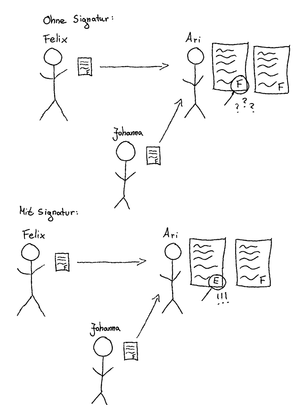
Zwar schützt dieses Verfahren soweit vor fremden Mitleser, aber es ist immernoch möglich, falsche Nachrichten im Namen von Felix zu versenden. Nehmen wir an, Johanna möchte Ari im Namen von Felix eine Nachricht senden. Mit dem bisherigen Verfahren kann Johanna ebenso Aris öffentlichen Schlüssel verwenden und Ari kann sich nicht sicher sein, ob die Nachricht tatsächlich von Felix stammt oder von Johanna.
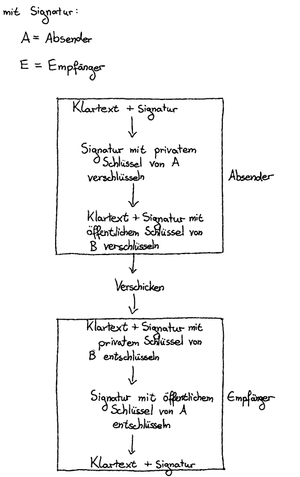
Um dieses Problem zu lösen, wird die Eigenschaft b genutzt. Einer Nachricht wird eine Signatur angehängt, die mit dem privaten Schlüssel ver- und mit dem öffentlichen Schlüssel entschlüsselt wird. Will also Felix nun Ari eine Nachricht schicken, so verschlüsselt er zuerst nur die Signatur mit seinem privaten Schlüssel, dann die ganze Nachricht mit Aris öffentlichem Schlüssel. Für die verschlüsselte Nachricht [math] C [/math] ergibt sich also
\[ C = E_A(D_F(M)) \]
Kommt die Nachricht nun bei Ari an, so entschlüsselt er zuerst die ganze Nachricht mit seinem privaten Schlüssel und dann die Signatur mit dem öffentlichen Schlüssel von Felix. Für die Entschlüsselung ergibt sich also
\[ M = D_A(E_F(C))) \]
Insgesamt ergibt sich also
\[ M = D_A(E_F(E_A(D_F(M)))) \]
Nun kann Ari anhand der Signatur erkennen, ob die Nachricht von Felix stammt, denn nur wenn der korrekte private Schlüssel verwendet wurde, ist die Signatur nun korrekt.
Team
Johanna Riedel, Felix Elser,Arianit Miftari