Fourieranalyse: Unterschied zwischen den Versionen
| Zeile 309: | Zeile 309: | ||
:<math> f(\omega ) = \int_{-\infty}^\infty F(t) e^{-i \omega t} dt </math> | :<math> f(\omega ) = \int_{-\infty}^\infty F(t) e^{-i \omega t} dt </math> | ||
| − | |||
<!-- Danielle --> | <!-- Danielle --> | ||
| Zeile 323: | Zeile 322: | ||
= \int_{-\infty}^\infty F(\tau)\delta(\tau -t) d\tau \\ | = \int_{-\infty}^\infty F(\tau)\delta(\tau -t) d\tau \\ | ||
= f(t) </math> | = f(t) </math> | ||
| + | |||
| + | ===Beispielhafte Berechnung einer Transformierten=== | ||
==Anwendungsbeispiele== | ==Anwendungsbeispiele== | ||
Version vom 13. September 2021, 12:29 Uhr
Die Fourier Reihe, bzw. die Fourier Transformation ist ein wichtiges Werkzeug der modernen Mathematik, Physik und Signalanalyse, und hat somit große praktische Bedeutung. Eine Fourierreihe ist eine Darstellung einer periodischen Funktion als Reihe von Sinus- und Kosinusschwingungen verschiedener Frequenzen. Die Fourier Transformation ist eine Verallgemeinerung hiervon; sie bildet auch aperiodische Funktionen auf ein Frequenzspektrum ab, bildlich gesprochen "wie viel von einer Frequenz in der Funktion vor kommt".
Ein klassisches Beispiel ist die Kompression von Audiodateien, beispielsweise MP3: Hierbei wird das gegebene Signal per Fouriertransformation in die einzelnen Frequenzen aufgespalten, sowieso nicht für Menschen hörbare, aber trotzdem vorhandene Frequenzen, werden gelöscht, und das ganze wird zu einer erheblich kleineren Datei rücktransformiert.
Fourier-Reihen
Summendarstellung
Wir betrachten zunächst eine bezüglich des Intervalls [math] [ - \pi, \pi][/math] [math]2 \pi[/math]-periodische, abschnittsweise stetige und integrierbare Funktion [math]f[/math].
Die Fourier-Reihe zu dieser Funktion [math] f[/math] ist eine Reihendarstellung aus komplexwertiger [math]e[/math]-Funktionen:
- [math] \displaystyle FS(f) = \sum_{k \in \mathbb{Z}} c_k e^{ikx}~, c_k \in \mathbb{C}[/math]
Dies lässt sich auch umschreiben:
- [math] \displaystyle FS(f) = \sum_{k = -\infty} ^ \infty c_k e^{ikx} = c_0 + \sum_{k = 1} ^\infty (c_k + c_{-k}) \cos (kx) + i(c_k - c_{-k}) \sin (kx) := \frac{a_0}{2} + \sum_{k = 1}^\infty a_k \cos (kx) + b_k \sin (kx) [/math]
mit [math] a_k = c_k + c_{-k} [/math], [math] b_k = i(c_k - c_{-k}) [/math] und insbesondere [math] a_0 = 2c_0 [/math]. Es ist ersichtlich, dass die [math]2\pi[/math]-periodische Funkion [math]f[/math] als gewichtete Summe aller [math]2\pi[/math]-periodischen Sinus und Kosinus dargestellt wird.
Berechnung der Koeffizienten
Ist eine Funktion [math]f[/math] gegeben, so müssen nur die Koeffizienten [math]c_k[/math] bestimmt werden. Hierfür ist folgende Beobachtung essenziell, für [math]k \neq 0[/math]:
- [math] \displaystyle \int_{-\pi}^ \pi e^{ikx} \text{d}x = \int_{-\pi}^{\pi} \cos (kx) \text{d}x + i \int_{-\pi}^{\pi} \sin (kx) \text{d}x = Big[- \frac{1}{m} \sin (kx) \Big]_{-\pi}^\pi + \Big[ i \frac{1}{m} \cos (kx) \Big]_{-\pi}^{\pi} = 0 [/math]
Für [math]k = 0[/math] ist das Integral trivialerweise 1. Somit gilt der Zusammenhang
- [math] \displaystyle \int_{-\pi}^\pi f(x) \text{d}x = \int_{-\pi}^\pi \sum_{k \in \mathbb{Z}} c_k e^{ikx} \text{d}x = \sum_{k \in \mathbb{Z}} \int_{-\pi}^\pi c_k e^{ikx} \text{d}x = c_0 [/math]
und
- [math] \displaystyle \int_{-\pi}^\pi f(x)\cdot e^{-inx} \text{d}x = \sum_{k \in \mathbb{Z}} \int_{-\pi}^\pi c_k e^{i(k-n) x} \text{d}x = c_n [/math]
Konvergenz einer Reihendarstellung
Um uns mit der Konvergenz einer Fourier-Reihe zu einer gegebenen Funktion zu befassen, definieren wir zunächst für ein [math] \: f: \mathbb{R} \rightarrow \mathbb{C} [/math] und ein [math] x \in \mathbb{R} [/math] im Fall der Existenz der jeweiligen Limiten
[math] f( x^+) := \lim_{t \searrow x} f(t) \: \: \: \: \: \: f( x^-) := \lim_{t \nearrow x} f(t) \: \: \: \: \: \: f(x^+_-) := \frac{f( x_+) + f( x^-)}{2} \\ f´( x^+) := \lim_{t \searrow 0} \frac{f(x+t)-f(x)}{t} \\ f´( x^-) := \lim_{t \nearrow 0} \frac{f(x+t)-f(x)}{t} [/math]
Nun können wir die zentrale Aussage dieses Abschnitts formulieren:
Konvergenzsatz von Dirichlet
Sei [math] \, f: \mathbb{R} \rightarrow \mathbb{R} \; 2\pi[/math]-periodisch und integrierbar auf [math] [ 0, 2π ] [/math]. Sei [math] x \in \mathbb{R} [/math] derart, dass [math] \, f( x^+), \, f( x^-), \, f´(x^+) \, [/math] und [math] \, f´(x^−) \, [/math] existieren. Dann gilt [math] \, FS(f)(x) = f(x^+_-) [/math].
Insbesondere gilt also, falls [math] \, f \, [/math] in [math]\, x \, [/math] differenzierbar ist, [math] \, FS(f)(x) = f(x) [/math].
| Beweis: |
| Wir definieren zunächst:
Für alle [math] n \in \mathbb{N} [/math] heiße die Funktion [math] D_n: \mathbb{R} \rightarrow \mathbb{C}, \; x \mapsto \sum_{k=-n}^n e^{ikx} \\ [/math] der n-te Dirichlet-Kern. Bevor wir mit dem eigentlichen Beweis des Satzes beginnen, lagern wir einige Aussagen in Hilfssätze aus: Lemma 1: (Sinusdarstellung der Dirichlet-Kerne) Für alle [math] n \in \mathbb{N} [/math] und alle [math] x \in \mathbb{R} \setminus \{ 2\pi a \, |\, a \in \mathbb{Z} \} [/math] gilt [math] D_n(x) = \frac{\sin(n x + \frac{x}{2})}{\sin(\frac{x}{2})} [/math]. Weiter ist [math] D_n(2 \pi a) = 2n + 1 [/math] für alle [math] \; a \in \mathbb{Z} [/math].
Sei [math] x \in \mathbb{R} \setminus \{ 2 \pi a | a \in \mathbb{Z} \} [/math]. Dann gilt [math] D_n(x) = \sum_{k=-n}^n e^{ikx} = e^{-inx} \sum_{k=0}^{2n} e^{ikx} [/math]. Da gilt [math] e^{inx} \neq 1 [/math], folgern wir aus der Formel der Partialsummen einer geometrischen Reihe [math] \begin{align} D_n &= e^{-inx} \frac{1-e^{i(2n+1)x}}{1-e^{ix}} \\ \\ &= \frac{e^{-inx}e^{-\frac{x}{2}}}{e^{-\frac{x}{2}}} \frac{e^{i(2n+1)x}-1}{e^{ix}} \\ \\ &= \frac{e^{i (n + \frac{1}{2}) x} − e^{−i (n + \frac{1}{2}) x}}{e^{\frac{i x}{2}} − e^{− i \frac{x}{2}}} \end{align} [/math] Nun folgern wir aus der Euler-Formel für beliebige [math] \varphi \in \mathbb{R} : \; e^{i \varphi} - e^{-i \varphi} = 2i \sin(\varphi) [/math]. Damit gilt [math] D_n(x) = \frac{\sin(nx + \frac{x}{2})}{\sin(\frac{x}{2})} [/math]. Des weiteren gilt für alle [math] a \in \mathbb{Z}: \; D_n(a2 \pi) = \sum_{k=-n}^{n}1 = 2n+1 [/math].
Lemma 2: Sei [math] \, f: \mathbb{R} \rightarrow \mathbb{C} \; 2 \pi [/math]-periodisch und integrierbar. Dann gilt für alle [math] n \in \mathbb{N}, \; x \in \mathbb{R} [/math] [math] \begin{align} FS_n(f)(x) &= \frac{1}{2 \pi} \int_{0}^{2 \pi} f(t) D_n(x-t) \, dt \\ &= \frac{1}{2 \pi} \int_{0}^{2 \pi} f(x-t) D_n(t) \, dt = \frac{1}{2 \pi} \int_{0}^{2 \pi} f(x+t) D_n(t) \, dt \end{align} [/math]
Sei [math] n \in \mathbb{N} [/math], dann gilt für alle [math] x \in \mathbb{R} [/math] laut der Formel für die Koeffizienten einer Fourier-Reihe [math] \begin{align} FS_n(f)(x) &= \frac{1}{2 \pi} \sum_{k=-n}^{n} \int_{0}^{2 \pi} f(t)e^{-ikx} \, dt \; e^{ikx} \\ &= \frac{1}{2 \pi} \int_{0}^{2 \pi} f(t) \sum_{k=-n}^{n} e^{ik(t-x)} \, dt \\ &= \frac{1}{2 \pi} \int_{0}^{2 \pi} f(t) D_n(x-t) \end{align} [/math]. Des weiteren können wir durch die Substitutionsregel mit [math] "t=x-y" [/math] folgern [math] \frac{1}{2 \pi} \int_{0}^{2 \pi} f(t) D_n(x-t) = \frac{1}{2 \pi} \int_{x}^{x-2 \pi} -f(x-y) D_n(y) \, dy [/math] Da [math] \, f [/math] und [math] D_n \; 2\pi[/math]-periodisch sind, gilt somit [math] \frac{1}{2 \pi} \int_{0}^{2 \pi} f(t) D_n(x-t) = \frac{1}{2 \pi} \int_{x}^{x-2 \pi} -f(x-y) D_n(y) \, dy = \frac{1}{2 \pi} \int_{0}^{2 \pi} f(x-t) D_n(t) \, dt [/math]. Analog zeigt man durch Substitution mit [math] t=x+y [/math] unter Verwendung von [math] D_n(-t) = D_n(t) [/math], dass gilt [math] \frac{1}{2 \pi} \int_{0}^{2 \pi} f(t) D_n(x-t) = \frac{1}{2 \pi} \int_{0}^{2 \pi} f(x+t) D_n(t) \, dt [/math].
Sei [math] \, f: [a,b] \rightarrow \mathbb{C} [/math] integrierbar. Dann gilt [math] \lim_{\lambda \rightarrow \infty} \int_a^b f(x) sin(\lambda x) \, dx = \lim_{\lambda \rightarrow \infty} \int_a^b f(x) cos(\lambda x) \, dx = 0 [/math] Selbiges gilt für [math] "\lambda \rightarrow -\infty" [/math]
[math] \begin{align} \Bigl| \int_a^b g(x) sin(\lambda x) \, dx \Bigl| &= \Bigl| \sum_{k=0}^{r-1} \int_{t_k}^{t_{k+1}} g(x) sin(\lambda x) \, dx \Bigl| \\ &= \Bigl| \sum_{k=0}^{r-1} c_k \int_{t_k}^{t_{k+1}} sin(\lambda x) \, dx \Bigl| \\ &= \Bigl| \sum_{k=0}^{r-1} c_k \Bigl[\frac {cos(\lambda x)}{\lambda} \Bigl]_{t_k}^{t_{k+1}} \, dx \Bigl| \\ &\leq \frac{2}{n} \Bigl| \sum_{k=1}^{r} c_k \Bigl|. \end{align} \\ \\ \Rightarrow \int_a^b g(x) sin(\lambda x) \, dx \overset{\lambda \rightarrow \infty}{\longrightarrow} 0 [/math]
[math] \Bigl| \int_a^b f(x)-g(x) \, dx \Bigl| \lt \frac{\varepsilon}{2} [/math]. (Die Integrierbarkeit von [math] \, f [/math] impliziert dessen Aproximierbarkeit durch Treppenfunktionen) Sei nun [math] N \in \mathbb{N} [/math] so gewählt, dass für alle [math] n \in \mathbb{N} [/math] gilt [math] n\gt N \Rightarrow \Bigl| \int_a^b g(x) sin(nx) \, dx \Bigl| \lt \frac{\varepsilon}{2} [/math]. Dann gilt für alle [math] n \gt N [/math] [math] \begin{align} \Bigl| \int_a^b f(x) sin(nx) \, dx \Bigl| &= \Bigl| \int_a^b (f(x)-g(x)) sin(nx) \, dx + \int_a^b g(x) sin(nx) \, dx \Bigl| \\ &\leq \Bigl| \int_a^b (f(x)-g(x)) sin(nx) \, dx \Bigl| + \Bigl| \int_a^b g(x) sin(nx) \, dx \Bigl| \\ &\leq \Bigl| \int_a^b (f(x)-g(x)) \, dx \Bigl| + \Bigl| \int_a^b g(x) sin(nx) \, dx \Bigl| \lt \frac{\varepsilon}{2} + \frac{\varepsilon}{2} = \varepsilon \end{align} [/math]
[math] \int_{- \pi}^{\pi} D_n(x) \, dx = \sum_{k=-n}^{n} \int_{- \pi}^{\pi} e^{ikx} \, dx = \int_{- \pi}^{\pi} e^{i0x} \, dx = 2\pi [/math]. Da nach der Sinusdarstellung der Dirichlet-Kerne gilt [math] D_n(x) = \frac{\sin(n x + \frac{x}{2})}{\sin(\frac{x}{2})} = \frac{-\sin(-n x - \frac{x}{2})}{-\sin(-\frac{x}{2})} = \frac{\sin(-n x - \frac{x}{2})}{\sin(-\frac{x}{2})} = D_n(-x) [/math], können wir folgern [math] \int_{- \pi}^{0} D_n(x) \, dx =\int_{0}^{\pi} D_n(x) \, dx = \pi [/math] Damit gilt [math] \; f(x^+_-) = \frac{1}{2 \pi} \int_{- \pi}^{0} f(x^+) D_n(x) \, dx + \frac{1}{2 \pi} \int_{0}^{\pi} f(x^-)D_n(x) \, dx. [/math] Unter Zuhilfenahme von Lemma 2 folgern wir [math] 2\pi \Bigl|FS_n(f)(x) − f (x^+_-)\Bigl| = \Bigl| \int_{- \pi}^{0} (f (x + t) − f (x^-)) Dn(t) \, dt + \int_{0}^{\pi} (f (x + t) − f (x^+)) Dn(t) \, dt \Bigl| [/math].
[math] g_+(t):=\frac{f(x+t)-f(x^+)}{t}\frac{t}{sin(\frac{t}{2})} [/math] für [math] t \in (0, \pi] [/math] Des weiteren sei [math] g_-(0):= \lim_{t \searrow 0} \frac{f(x+t)-f(x^-)}{sin(\frac{t}{2})}, \; \lim_{t \nearrow 0} \frac{f(x+t)-f(x^-)}{sin(\frac{t}{2})} [/math] (Da laut Annahme [math] f´(x^-), \, f´(x^+) [/math] existieren und [math] \frac{d}{dt} \Bigl(sin(\frac{t}{2})\Bigl)(0) = \frac{1}{2} \neq 0 [/math] gilt, gibt es die entsprechenden Limiten) Nun können wir die Sinusdarstellung der Dirichlet-Kerne in die obige Formel einsetzen und erhalten [math] 2\pi \Bigl|FS_n(f)(x) − f (x^+_-)\Bigl| = \Bigl| \int_{- \pi}^{0} g_- sin((n + \frac{1}{2})t) \, dt + \int_{0}^{\pi} g_+ sin((n + \frac{1}{2})t) \, dt \Bigl| [/math]. (Zwar gilt [math] (f (x + t) − f (x^-)) Dn(t) = g_- sin((n + \frac{1}{2})t) [/math] und [math] (f (x + t) − f (x^+)) Dn(t)=g_+ sin((n + \frac{1}{2})t) [/math] lediglich für alle [math] t \in \mathbb{R} \setminus \{ 2\pi a \, |\, a \in \mathbb{Z} \} [/math], das reicht aber aus, um die Gleichheit der jeweiligen Integrale zu gewährleisten)
[math] 2\pi \Bigl|FS_n(f)(x) − f (x^+_-)\Bigl| \; \overset{n \rightarrow \infty}{\longrightarrow} \; 0 \\ \Rightarrow FS(f)(x) = f(x^+_-) [/math] |
Beispiele
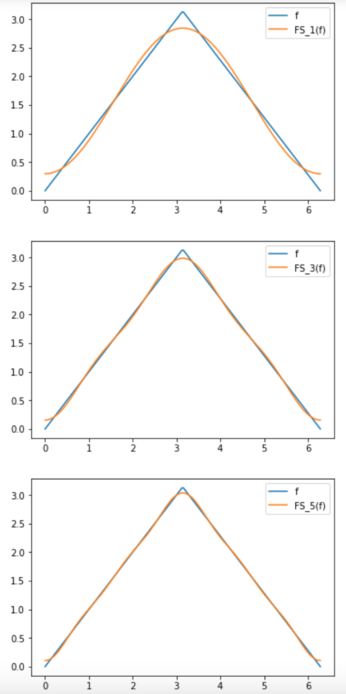
Beispiel 1:
Sei [math] \, f: \mathbb{R} \rightarrow \mathbb{R} \; 2 \pi [/math]-periodisch und auf [math] [0, 2 \pi) [/math] gegeben durch
[math] f(x):= \begin{cases} x, \; 0 \leq x \leq \pi \\ \\ 2\pi - x, \pi \lt x \lt 2 \pi\; \end{cases} [/math]
Da [math] \, f [/math] stetig ist und für alle [math] x \in \mathbb{R} \; \; f´(x^-), \, f´(x^+) [/math] existieren, gilt nach dem Satz von Dirichlet [math] \, f=FS(f) [/math]. Im folgenden berechnen wir, wie oben beschrieben, die Koeffizienten dieser Fourier-Reihe:
[math] \begin{align} a_0 &= \frac{1}{\pi} \int_0^{2\pi} f(x) \, dx \\ &= \frac{2}{\pi} \int_0^{\pi} x \, dx = \frac{2 \pi^2 }{ 2 \pi} = \pi \end{align} [/math]
Sei nun [math] n \in \mathbb{R} [/math], dann gilt
[math] \begin{align} a_n &= \frac{1} {\pi} \int_0^{2\pi} f(x) cos(nx) \, dx \\ &= \frac{1} {\pi} \Bigl( \int_0^{\pi} xcos(nx) \, dx + \int_{\pi}^{2\pi} 2\pi cos(nx) \, dx - \int_{\pi}^{2\pi} xcos(nx) \, dx \Bigl) \\ &= \frac{1} {\pi} \Bigl( 2\int_0^{\pi} xcos(nx) \, dx + \int_{\pi}^{2\pi} 2\pi cos(nx) \, dx \Bigl)\\ &= \frac{1} {\pi} \Bigl(2\int_0^{\pi} xcos(nx) \, dx + \Bigl[ \frac{2\pi}{n} sin(nx) \Bigl]_{\pi}^{2\pi} \Bigl)\\ &= \frac{1} {\pi} \Bigl( 2\int_0^{\pi} xcos(nx) \, dx + 0 \Bigl) \end{align} [/math].
Weiter können wir durch partielle Integration berechnen:
[math] \begin{align} a_n &= \frac{2}{\pi} \Bigl( \Bigl[\frac{x}{n} sin(nx) \Bigl]_{0}^{\pi} - \int_0^{\pi} \frac{1}{n} sin(nx) \, dx \Bigl) \\ \\ &= \frac{2}{\pi} \Bigl( 0 - \Bigl[ \frac{1}{n} cos(nx) \Bigl]_{0}^{\pi} \Bigl) \\ \\ &= -\frac{2}{\pi} \Bigl[\frac{1}{n^2} cos(nx) \Bigl]_{0}^{\pi} \\ \\ &= \begin{cases} 0, \; \text{falls}\, n \, \text{gerade ist} \\ \\ -\frac{4}{\pi n^2}, \; \text{falls}\, n \, \text{ungerade ist} \end{cases} \end{align} [/math]
Des weiteren gilt:
[math] \begin{align} b_n &= \frac{1} {\pi} \int_0^{2\pi} f(x) sin(nx) \, dx \\ \\ &= \frac{1} {\pi} \Bigl( \int_0^{\pi} f(x) sin(nx) \, dx + \int_{\pi}^{2\pi} f(x) sin(nx) \, dx \Bigl) \end{align} [/math].
Da aber für alle [math] \, x \in [0,\pi] [/math] gilt, [math] f(x)sin(x) = -f(x + \pi)sin(x+\pi) [/math] können wir daraus folgern [math] b_n = 0 [/math].
Damit gilt
[math] f(x) = FS(f)(x) = \frac{\pi}{2} - \frac{4}{\pi} cos(x) - \frac{4}{9\pi} cos(3x) - \frac{4}{25\pi} cos(5x) - \frac{4}{49\pi} cos(7x) \dots [/math].
Außerdem können stellen wir fest, dass für alle [math] \, n \in \mathbb{N} [/math] gilt
[math] \sum_{k = 0}^{n} |a_k| \leq \frac{\pi}{2} + \frac{4}{\pi} \sum_{k = 0}^{n} \frac{1}{k^2} [/math].
Da die verallgemeinerte geometrische Reihe [math] \sum_{k = 0}^{\infty} \frac{1}{k^\alpha} [/math] für [math] \alpha = 2 [/math] konvergiert, tut dies auch [math] \sum_{k = 0}^{\infty} |a_k| [/math]. Des weiteren gilt für alle [math] \, n \in \mathbb{N} [/math]
[math] \max_{x \in \mathbb{R}} |cos(nx)| = 1 [/math].
und wir können abschätzen:
[math] \sup_{x \in \mathbb{R}} |FS_n(f)(x) - f(x)| \leq \sum_{k = n + 1}^{\infty} |a_k| [/math]
Somit konvergiert die Fourier-Reihe zu [math] \, f [/math] nicht nur punktweise, wie es der Satz von Dirichlet besagt, sondern auch gleichmäßig.
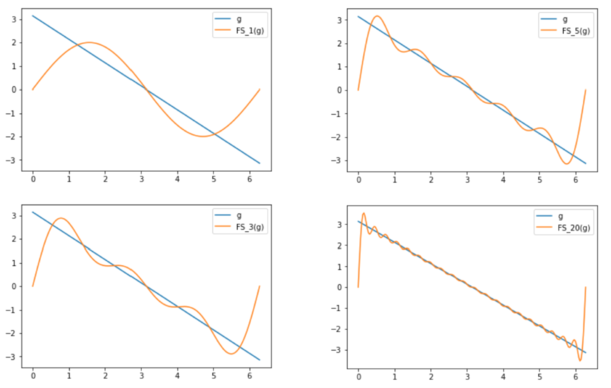
Beispiel 2: (Sägezahnfunktion)
Sei [math] g: \mathbb{R} \rightarrow \mathbb{R} \; 2 \pi [/math]-periodisch und auf [math] [0, 2 \pi) [/math] gegeben durch
[math] g(x):= \pi - x [/math]
Nach dem Satz von Dirichlet konvergiert die Fourier-Reihe zu [math] g [/math] punktweise und nimmt dabei überall mit Außnahme der Sprungstellen den selben Wert wie [math] g [/math] an. Nun berechnen wir die Koeffizienten auch dieser Fourier-Reihe:
Zuerst stellen wir fest, dass für alle [math] n \in \mathbb{N}_0 [/math] gilt
[math] \begin{align} a_n &= \frac{1} {\pi} \int_0^{2\pi} g(x) cos(nx) \, dx \\ &= \frac{1} {\pi} \Bigl( \int_0^{\pi} g(x) cos(nx) \, dx + \int_{\pi}^{2\pi} g(x) cos(nx) \, dx \Bigl) \end{align} [/math]
Da aber gilt [math] g(\pi +x)cos(\pi + x) = - g(\pi - x)cos(\pi - x) [/math], folgt:
[math] \int_0^{\pi} g(x) cos(nx) \, dx = -\int_{\pi}^{2\pi} g(x) cos(nx) \, dx \; \Rightarrow \; a_n = 0 [/math]
Weiter berechnen wir
[math] \begin{align} b_n &= \frac{1} {\pi} \int_0^{2\pi} g(x) sin(nx) \, dx \\ &= \frac{1} {\pi} \int_0^{2\pi} (\pi - x ) sin(nx) \, dx \\ &= - \frac{1} {\pi} \int_0^{2\pi} x sin(nx) \, dx + \frac{1} {\pi} \int_0^{2\pi} sin(nx) \, dx \\ &= - \frac{1} {\pi} \int_0^{2\pi} x sin(nx) \, dx \end{align} [/math].
Nun verwenden wir partielle Integration, um zu schließen
[math] \begin{align} b_n &= \frac{1} {\pi n} \Bigl( \Bigl[ xcos(nx) \Bigl]_{0}^{2 \pi} - \int_0^{2\pi} cos(nx) \, dx \Bigl) \\ &= \frac{1} {\pi n} \Bigl[ xcos(nx) \Bigl]_{0}^{2 \pi} = \frac{2 \pi} {\pi n} = \frac{2}{n} \end{align} [/math]
Somit besitzt die Fourier-Reihe zu [math] g [/math] folgende Darstellung:
[math] 2 \sum_{n = 1}^{\infty} \frac{sin(nx)}{n} [/math]
Wir stellen fest, dass die Reihe [math] \sum_{n = 1}^{\infty} b_n [/math] nicht konvergiert, da sie bis auf den Vorfaktor [math] 2 [/math] der divergenten harmonischen Reihe entspricht. Dies ist wenig überraschend, da die Fourier-Reihe zu [math] g [/math] andernfalls gleichmäßig konvergieren müsste, da sich der Beweis der gleichmäßigen Konvergenz der Reihe aus Beispiel 1 analog für [math] FS(g) [/math] führen ließe. Dass sie dies nicht tut, ist daran zu erkennen, dass [math] FS(g) [/math] nach dem Satz von Dirichlet an den Sprungstellen von [math] g [/math] nicht stetig sein kann, aber alle Summanden der Reihe stetige Funktionen sind, eine Eigenschaft die unter gleichmäßiger Konvergenz erhalten bliebe.
Anschaulich äußert sich die fehlende gleichmäßige Konvergenz darin, dass die Partialsummen von [math] FS(g) [/math] an den Intervallgrenzen "überschwingen", wodurch die Reihe dort sehr viel langsamer konvergiert.
Zeichnen mit Fourierreihen
Fouriertransformation
Anschauung
Die Fouriertransformation ist ein Teil der Fourieranalyse. Es geht dabei darum, aus aperiodischen Signale ein kontinuierliches Spektrum zu transformieren. Dies gelingt mittels einer Integraltransformation. Wir wollen eine zeitabhängige Funktion in eine frequenzabhängige transformieren. Diese Transformation stellt sich wie folgt dar:
- [math] f(\omega ) = \int_{-\infty}^\infty F(t) e^{-i \omega t} dt [/math]
Inverse Fouriertransformation
Diese Transformation ist invertierbar. Dies nennt man dann die inverse Fouriertransformation. Diese Umkehrung stellt sich wie folgt dar:
- [math]F(x) = \frac{1}{2\pi}\int_{-\infty}^{\infty} f(\omega)e^{i\omega t} d\omega[/math]
Beweis der Inversen
Nun wollen wir nachweisen, dass dies tatsächlich die Inverse der Fourier Transformation ist. Dafür setzen wir für [math]f(\omega)[/math] die obige Gleichung für die Transformation ein:
- [math]\frac{1}{2\pi}\int_{-\infty}^{\infty} f(\omega)e^{i\omega t} d\omega \\ = \frac{1}{2\pi}\int_{\omega = -\infty}^{\infty} (\int_{\tau = -\infty}^{\infty}F(\tau)e^{-i\omega \tau}d\tau)e^{i\omega t} d\omega \\ =\frac{1}{2\pi}\int_{\tau = -\infty}^{\infty} F(\tau)(\int_{\omega = -\infty}^{\infty}e^{-i\omega (\tau -t)}d\omega) d\tau \\ = \int_{-\infty}^\infty F(\tau)\delta(\tau -t) d\tau \\ = f(t) [/math]
Beispielhafte Berechnung einer Transformierten
Anwendungsbeispiele
Die Fouriertransformation findet in einigen Bereichen Anwendung.
- Kompressionsverfahren: Mithilfe der Fouriertransformation können MP3-Dateien in die Frequenzen zerlegt werden. Nun können solche, welche für den Menschen sowieso nicht wahrnehmbar sind aussortiert werden und die Datei somit verkleinert.
- Magnetresonanztherapie: Bei dieser Therapie werden bestimmte Atome durch Magnetwellen in Schwingung versetzt und ihre Resonanz gemessen. Mithilfe der Fouriertransformation werden die Frequenzanteile in horizontale und vertikale geteilt. Anschließend erhält man eine Kombination aus Phasen- und Frequenzkodierung. Diese können mithilfe der inversen Fouriertransformation in ein dreidimensionales Bild umgewandelt werden.
- Klangaufbereitung: Mithilfe der Fouriertransformation können störende hochfrequentische Klänge gefunden und eliminiert werden.
Quellen
- https://de.wikipedia.org/wiki/Fourierreihe Wikipedia: Fourierreihe
- https://en.wikipedia.org/wiki/Fourier_series Wikipedia: Fourier series
- https://www.youtube.com/watch?v=spUNpyF58BY 3Blue1Brown: But what is the Fourier Transform? A visual introduction.
- https://www.youtube.com/playlist?list=PL0S2AA6W_m55xj9EaL9mGsLRHd6z7Y3y5 Khan Akademy: Fourier Series
- https://www.youtube.com/watch?v=r6sGWTCMz2k 3BlueBrown: But what is a Fourier series? From heat flow to drawing with circles | DE4
- https://www.aleph1.info/?call=Puc&permalink=analysis2_4_Z3 Oliver Deiser: Analysis 2 | Der Konvergenzsatz von Dirichlet
- http://www.num.uni-sb.de/rjasanow/dokuwiki/lib/exe/fetch.php?media=lehre:vorlesung:fourier-reihen.pdf Universität des Saarlandes, Prof. Dr. Sergej Rjasanow: Fourier-Reihen
- C. Schnörr: HM-2 für Physiker 2021, Fourierreihen (via MaMpf)
- Hans-Heinrich Körle: Die phantastische Geschichte der Anlaysis, Oldenbourg Verlag, 2. Auflage 2012
- https://web.stanford.edu/class/ee102/lectures/fourtran