Die Keplerschen Gesetze und das Zweikörperproblem: Unterschied zwischen den Versionen
YMitev (Diskussion | Beiträge) |
YMitev (Diskussion | Beiträge) |
||
| Zeile 7: | Zeile 7: | ||
Im Weiteren nahm Kepler 3 der Beobachtungen von Tycho, als sich Mars auf der gleichen Position entlang seiner Bahn befand und versuchte, die Position von der Erde auf ihrer Bahn zu bestimmen. Das gab ihm 3 verschiede Punkte auf der Bahn von der Erde (die Umlaufszeit vom Mars ist nicht durch die Umlaufszeit von der Erde teilbar) und er konnte das Zentrum des dadurch eindeutig bestimmten Kreises bestimmen. Er bekam einen verschiedenen Wert der [https://de.wikipedia.org/wiki/Exzentrizit%C3%A4t_(Mathematik) Exzentrizität] der Erde als den Wert aus der Theorie von Tycho, was insbesondere bedeutete, dass das Zentrum der Erde nicht mit dem [https://de.wikipedia.org/wiki/Epizykeltheorie#Ptolem%C3%A4isches_Weltbild Epizykel] von Ptolemäus übereinstimmte. Das inspirierte ihm, die erwähnte Hypothese zu formulieren. | Im Weiteren nahm Kepler 3 der Beobachtungen von Tycho, als sich Mars auf der gleichen Position entlang seiner Bahn befand und versuchte, die Position von der Erde auf ihrer Bahn zu bestimmen. Das gab ihm 3 verschiede Punkte auf der Bahn von der Erde (die Umlaufszeit vom Mars ist nicht durch die Umlaufszeit von der Erde teilbar) und er konnte das Zentrum des dadurch eindeutig bestimmten Kreises bestimmen. Er bekam einen verschiedenen Wert der [https://de.wikipedia.org/wiki/Exzentrizit%C3%A4t_(Mathematik) Exzentrizität] der Erde als den Wert aus der Theorie von Tycho, was insbesondere bedeutete, dass das Zentrum der Erde nicht mit dem [https://de.wikipedia.org/wiki/Epizykeltheorie#Ptolem%C3%A4isches_Weltbild Epizykel] von Ptolemäus übereinstimmte. Das inspirierte ihm, die erwähnte Hypothese zu formulieren. | ||
| − | Unter Beachtung seiner Hypothese machte Kepler ziemlich langwierige Berechungen über die Erdbahn, indem er ganz viele Punkte auf der Bahn nahm und für die alle die Distanz | + | Unter Beachtung seiner Hypothese machte Kepler ziemlich langwierige Berechungen über die Erdbahn, indem er ganz viele Punkte auf der Bahn nahm und für die alle die Distanz zur Sonne berechnete. Er legte auf diese Weise den heliozentrischen Längengrad von der Erde fest, welcher sich nur mit höhstens 9 Winkelsekunden von dem Ergebis aus der Theorie von Tycho untershied. Der Ursprung seines zweiten Gesetzes(Flächensatz) befindet sich genau in diesen Berechnungen. Spannend ist es, dass die Formulierung des Gesetzes erst spät in seinem Buch ''Astronomia Nova'' kommt (Seite ~230). Der Grund dafür ist, dass Kepler im Gegensatz zu den anderen Astronomen Schritt für Schritt den tatsächlichen Fortgang seiner jahrelangen Arbeit beschrieb. Ausgehend von dem Gesetz konnte Kepler zusammen mit den Daten von Tycho die Position vom Mars auf der Bahn festlegen. |
| − | + | Durch einen Vergleich mit seiner vorherigen Theorie stellte er fest, dass der Mars sich in manchen Regionen seiner Bahn schneller und in anderen langsamer bewegt. Mit weiterem Nachrechnen schloss Kepler ab, dass die Bahn ovalförmig sein musste. Mit den neuen Annahmen über die Form der Bahn und der Geschwindigkeitsänderung entlang der Bahn hat Kepler eine [https://en.wikipedia.org/wiki/Ellipse Ellipse] mit der Sonne in einem der Brennpunkte für die ovalförmige Bahn vom Mars angenommen und führte nochmals seine Berechnungen durch. Das Ergebnis war hervorragend, denn die neue Theorie konnte die Position vom Mars auf der Planetenbahn exakt festlegen und lieferte nur kleine Fehler für den heliozentrischen Längengrad. Bei dem weiteren Studium der Planetenbahn von Mars hat Kepler sein erstes Gesetz formuliert. | |
| − | Im Jahr 1619 unter dem Titel ''Harmonices mundi'' („Harmonien der Welt“) hat Kepler eine | + | Im Jahr 1619 unter dem Titel ''Harmonices mundi'' („Harmonien der Welt“) hat Kepler eine genauere Erklärung des gesamten Systems und der Beziehungen der Planetenbahnen gegeben. Dort findet sich auch der Satz, der später als das dritte Keplersche Gesetz bekannt wurde. |
==Beweis der Gesetze== | ==Beweis der Gesetze== | ||
Version vom 4. Oktober 2021, 19:10 Uhr
Geschichte der Gesetze
Kepler strebte nach einer "physikalischen" Erklärung des Sonnensystems, das sich in einfachen Zahlenbeziehungen auffinden lässt. Er arbeitete mit der Überzeugung, dass das heliozentrische System von Kopernikus(1543) richtig war. Letzteres konnte die Größe aller Planetenbahnen im Verhältniss zur Größe der Erdbahn eindeutig festlegen. Zur Erklärung dieser Verhältnisse beschäftigte sich Kepler mit der Bahn vom Mars. Es war ihm klar, dass die Bahn vom Mars keinen Kreis darstellt und am Anfang seiner Arbeit Astronomia Nova 1609 hatte er "physikalische" Vermutungen getroffen, die ihn bei seiner Suche nach der genauen Form der Bahn sowie der Geschwindigkeit des Planets entlang seiner Bahn begleiteten .
Die Daten aus den Himmelsbeobachtungen von Tycho standen ihm zur Verfügung. Glücklicherweise waren sie für damals ziemlich genau (Unsicherheit von 2-3 Winkelminuten) . Bei der Auswertung der Daten von Tycho formulierte Kepler eine Theorie über den heliozentrischen Längengrad vom Mars, welche auch die Distanz zwischen Mars und der Sonne festlegte. Auf der anderer Seite hatte Tycho eine Theorie über den heliozentrischen Längengrad der Erde entwickelt. Kepler konnte seine Ergebnisse mit dieser Theorie vergleichen, indem er das Dreieck, gebildet von der Erde, der Sonne und dem Mars, untersucht hatte. Beide Theorien waren unter der Annahme gebildet, dass es eine "mittlere Sonne" gibt (von Ptolemäus erstmals eingeführt und von Kopernikus in den leeren Mittelpunkt desjenigen Kreises gesetzt, den Kopernikus der Erde zugewiesen hatte), welche die Planetenbewegungen verursachte. Kepler stellte aber mit der Auswertung des Fehlers der Distanz zwischen Mars und der Sonne im Vergleich zu dem Ergebnis aus der Theorie von Tycho fest, dass die Annahmen seiner Theorie falsch waren und das brachte ihn zu der Hypothese, dass die Geschwindigkeit der Planeten auf der Planetenbahn nicht überall konstant ist, sondern von der Distanz zur Sonne abhängt.
Im Weiteren nahm Kepler 3 der Beobachtungen von Tycho, als sich Mars auf der gleichen Position entlang seiner Bahn befand und versuchte, die Position von der Erde auf ihrer Bahn zu bestimmen. Das gab ihm 3 verschiede Punkte auf der Bahn von der Erde (die Umlaufszeit vom Mars ist nicht durch die Umlaufszeit von der Erde teilbar) und er konnte das Zentrum des dadurch eindeutig bestimmten Kreises bestimmen. Er bekam einen verschiedenen Wert der Exzentrizität der Erde als den Wert aus der Theorie von Tycho, was insbesondere bedeutete, dass das Zentrum der Erde nicht mit dem Epizykel von Ptolemäus übereinstimmte. Das inspirierte ihm, die erwähnte Hypothese zu formulieren.
Unter Beachtung seiner Hypothese machte Kepler ziemlich langwierige Berechungen über die Erdbahn, indem er ganz viele Punkte auf der Bahn nahm und für die alle die Distanz zur Sonne berechnete. Er legte auf diese Weise den heliozentrischen Längengrad von der Erde fest, welcher sich nur mit höhstens 9 Winkelsekunden von dem Ergebis aus der Theorie von Tycho untershied. Der Ursprung seines zweiten Gesetzes(Flächensatz) befindet sich genau in diesen Berechnungen. Spannend ist es, dass die Formulierung des Gesetzes erst spät in seinem Buch Astronomia Nova kommt (Seite ~230). Der Grund dafür ist, dass Kepler im Gegensatz zu den anderen Astronomen Schritt für Schritt den tatsächlichen Fortgang seiner jahrelangen Arbeit beschrieb. Ausgehend von dem Gesetz konnte Kepler zusammen mit den Daten von Tycho die Position vom Mars auf der Bahn festlegen.
Durch einen Vergleich mit seiner vorherigen Theorie stellte er fest, dass der Mars sich in manchen Regionen seiner Bahn schneller und in anderen langsamer bewegt. Mit weiterem Nachrechnen schloss Kepler ab, dass die Bahn ovalförmig sein musste. Mit den neuen Annahmen über die Form der Bahn und der Geschwindigkeitsänderung entlang der Bahn hat Kepler eine Ellipse mit der Sonne in einem der Brennpunkte für die ovalförmige Bahn vom Mars angenommen und führte nochmals seine Berechnungen durch. Das Ergebnis war hervorragend, denn die neue Theorie konnte die Position vom Mars auf der Planetenbahn exakt festlegen und lieferte nur kleine Fehler für den heliozentrischen Längengrad. Bei dem weiteren Studium der Planetenbahn von Mars hat Kepler sein erstes Gesetz formuliert.
Im Jahr 1619 unter dem Titel Harmonices mundi („Harmonien der Welt“) hat Kepler eine genauere Erklärung des gesamten Systems und der Beziehungen der Planetenbahnen gegeben. Dort findet sich auch der Satz, der später als das dritte Keplersche Gesetz bekannt wurde.
Beweis der Gesetze
Voraussetzung
Kepler versuchte Gesetze zu formulieren, die die Planetenbewegung beschreiben. Seine Überlegungen gingen von einem heliozentrischen Weltbild, auch Kopernikanischen Weltbild genannt, aus. Hierbei ist die Sonne ein fixes Zentrum des Universums und die Planeten bewegen sich um sie herum. Mit Hilfe von Beobachtungswerten, vor allem der Marsbahn, schloss er, dass die Planeten sich nicht auf idealen Kreisbahnen bewegen. Seine Gesetze sind folglich empirisch. Ihre Gültigkeit lässt sich jedoch mit heutigem Wissen belegen.
Das erste Gesetz (Ellipsensatz) lässt sich mittels der Clairautschen Differentialgleichung beweisen, hier jedoch angewendet mit [math]i=0[/math] und Ellipsengeometrie.
Das zweite Gesetz (Flächensatz) folgt aus der Drehimpulserhaltung.
Das dritte Gesetz lässt sich mittels der Newtonschen Gesetze direkt beweisen.
Erstes Keplersches Gesetz (Ellipsensatz)
Himmelskörper bewegen sich auf elliptischen Umlaufbahnen um das Baryzentrum herum.
Das Baryzentrum bildet den gewichteten Massenmittelpunkt mehrerer Massen (Brennpunkte). Im Falle der Planeten unseres Sonnensystems bildet die Sonne einen dieser Brennpunkte. Der andere Brennpunkt ist leer. Dies ergibt sich aus Newtons Gravitationsgesetz, da die Masse des Zentralkörpers (hier die Sonne) wesentlich größer als die der Planeten ist und die Wirkung der Planeten auf die Sonne vernachlässigt werden kann.
Herleitung
1. Die Bewegung eines Planeten um einen Zentralkörper unter dem Einfluss der Gravitationskraft verläuft in einer Ebene
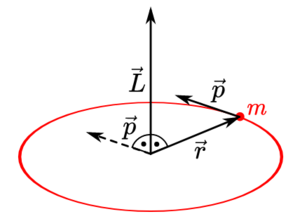
Der Bewegung der Planeten zugrunde liegt der Drehimpuls. Der Drehimpulsvektor [math]\vec{L}[/math] ist definiert als das Kreuzprodukt seines Ortsvektor [math]\vec{r}[/math] und seines Impulsvektor [math]\vec{p}[/math]:
- [math]\vec{L} = \vec{r} \times \vec{p}[/math]
Daraus ergibt sich, dass der Drehimpuls [math]\vec{L}[/math] senkrecht zum Ortsvektor [math]\vec{r}[/math] und zum Impulsvektor [math]\vec{p}[/math] gerichtet ist. Jedoch müssen der Ortsvektor [math]\vec{r}[/math] und der Impulsvektor [math]\vec{p}[/math] nicht notwendigerweise senkrecht zueinander stehen. In der klassischen Mechanik ergibt dich der Impulsvektor [math]\vec{p}[/math] aus dem Produkt der Masse [math]m[/math] des bewegten Körpers und der Geschwindigkeit [math]\vec{v}[/math]. Folglich gilt wegen [math]\vec{p} = m \cdot \vec{v}[/math] für den Drehimpuls:
- [math]\vec{L} = \vec{r} \times \vec{p} = m \cdot (\vec{r} \times \vec{v})[/math]
Bleibt nun der Drehimpuls des bewegten Körpers im Laufe der Zeit konstant, dann liegen Ortsvektor [math]\vec{r}[/math] und Geschwindigkeit [math]\vec{v}[/math] fortwährend in einer gemeinsamen Ebene, in der dann der Körper rotiert. Mit Hilfe der zeitlichen Ableitung des Drehimpulses lässt sich nachweisen, dass bei der Bewegung eines Planeten um einen Zentralkörper unter dem Einfluss der Gravitationskraft der Drehimpuls des Trabanten konstant bleibt.
- [math]\frac{d}{dt}\vec{L} = \frac{d}{dt}(\vec{r} \times \vec{p}) = \frac{d}{dt}(\vec{r} \times m \cdot \vec{v}) = m \cdot \frac{d}{dt}(\vec{r} \times \vec{v}) = m\cdot(\vec{r} \times \vec{a}) = (\vec{r} \times m \cdot \vec{a}) = \vec{r} \times \vec{F}[/math]
Da die Gravitationskraft [math]\vec{F}[/math] auf den Planeten stets in Richtung des Zentralkörpers und somit entgegengesetzt zum Ortsvektor [math]\vec{r}[/math] gerichtet ist, ist das Kreuzprodukt von [math]\vec{r}[/math] und [math]\vec{F}[/math] folglich der Nullvektor [math]\vec{0}[/math]:
- [math]\vec{r} \times \vec{F} = \vec{0}[/math]
Damit ergibt sich:
- [math]\frac{d}{dt}\vec{L} = \vec{r} \times \vec{F} = \vec{0} \Rightarrow \vec{L} = \vec{r} \times \vec{p} = m \cdot (\vec{r} \times \vec{v})\enspace \text{ist konstant}[/math]
Hieraus ergibt sich, dass die Bewegung eines Planeten um einen Zentralkörper unter dem Einfluss der Gravitationskraft in einer Ebene verläuft.
2. Die Bewegung eines Planeten um einen Zentralkörper unter dem Einfluss der Gravitationskraft verläuft auf einer Ellipsenbahn
Periodische Bewegungen, die in einer Ebene stattfinden, beschreibt man am einfachsten durch sogenannte Polarkoordinaten. Es ergibt sich:
- [math] \begin{align*} x &= r \cdot \cos(\varphi)\\ y &= r \cdot \sin(\varphi) \end{align*}[/math]
Daraus lassen sich die Geschwindigkeitskoordinaten [math]v_x = \dot{x}[/math] und [math]v_y = \dot{y}[/math] errechnen. Mit der Winkelgeschwindigkeit [math]\omega = \dot{\varphi}[/math] ergibt sich:
- [math] \begin{align*} \dot{x} &= \dot{r} \cdot \cos(\varphi) - r \cdot \sin(\varphi) \cdot \omega\\ \dot{y} &= \dot{r} \cdot \sin(\varphi) + r \cdot \cos(\varphi) \cdot \omega\\ \end{align*}[/math]
Die Gesamtenergie [math]E_{ges}[/math] eines Planeten bei der Bewegung um einen Zentralkörper lässt sich durch Polarkoordinaten ausdrücken. Hierfür nutzen wir folgendes:
- [math]m =[/math] Masse des Planeten. [math]M =[/math] Masse des Zentralkörpers.
- Als Radius [math]r[/math] aus dem Term für die potenzielle Energie verwenden wir die Polarkoordinate [math]r[/math].
- Das Geschwindigkeitsquadrat [math]v^2 = v^{2}_x + v^{2}_y[/math] aus der kinetischen Energie schreibt sich in Polarkoordinaten [math]v^2 = \dot{r}^{2} + r^2 \cdot \omega^{2}\enspace \enspace [/math] (1).
- Der Drehimpuls [math]\vec{L}[/math] hat den konstanten Betrag [math]L=m \cdot r^2\cdot \omega\enspace \enspace [/math] (2).
- Aus der Gleichung zum Bahndrehimpuls folgt [math]L = m \cdot r^2 \cdot \omega \Leftrightarrow \omega = \frac{L}{m \cdot r^2}\enspace \enspace [/math](3).
- [math] \begin{align*}E_{ges} &= E_{kin} + E_{pot}\\ &= \frac{1}{2} \cdot m\cdot v^2 - \frac{G \cdot m \cdot M}{r}\\ &\stackrel{\text{(1)}}{=} \frac{1}{2} \cdot m\cdot (\dot{r}^{2} + r^2 \cdot \omega^{2}) - \frac{G \cdot m \cdot M}{r}\\ &\stackrel{\text{(2)}}{=} \frac{1}{2} \cdot \left(m\cdot \dot{r}^{2} + \frac{L}{m \cdot r^2}\right) - \frac{G \cdot m \cdot M}{r}\\ &\stackrel{\text{(3)}}{=} \frac{1}{2} \cdot \left(\frac{L^2}{m \cdot r^4}\left(\frac{dr}{d\varphi}\right)^2 + \frac{L}{m \cdot r^2}\right) - \frac{G \cdot m \cdot M}{r} \end{align*}[/math]
Aufgelöst nach [math]\frac{dr}{d\varphi}[/math] erhält man aus der Gleichung:
- [math]\frac{dr}{d\varphi}=\frac{m\cdot r^2}{L}\cdot \sqrt{\frac{2\cdot E_{ges}}{m} + \frac{2\cdot G\cdot M}{r}-\frac{L}{m^2\cdot r^2}}[/math]
Nach [math]d\varphi[/math] aufgelöst, erhalten wir:
- [math]d\varphi = \frac{L}{m \cdot r^2}\cdot \frac {1}{\sqrt{\frac{2 \cdot E_{ges}}{m} + \frac{2 \cdot G \cdot M}{r} -1 \frac{L}{m^2 \cdot r^2}}}\cdot dr[/math]
Mit Hilfe von Substitution lässt sich die Bewegungsgleichung integrieren, so erhalten wir durch Umformungen und Resubstitution die Polarkoordinatendarstellung eines Kegelschnittes:
- [math]r(\varphi) = \frac{p}{1-\varepsilon \cdot \cos \left(\varphi \right)}[/math]
mit [math]p := \frac{L^2}{m^2\cdot G\cdot M}[/math] und [math]\varepsilon := \frac{\alpha \cdot L}{G\cdot M\cdot m}[/math]
Aus dieser Gleichung lässt sich, abhängig von [math]\varepsilon[/math], bestimmen, ob sich der Himmelskörper bezüglich des Zentralkörpers in einer Ellipse, Parabel oder Hyperbel bewegt.
Nachweis der Ellipsenbahn
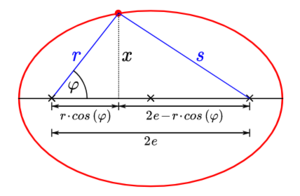
Wir betrachten nun eine Ellipse mit der großen Halbachse [math]a := \frac{p}{1 - \varepsilon^2}[/math] (I), der kleinen Halbachse [math]b := \frac{p}{\sqrt{1-\varepsilon^2}}[/math] (II) und dem Abstand vom Mittelpunkt zu den Brennpunkten [math]e := a\cdot \varepsilon[/math] (III).
Aus (I), (II) und (III) ergibt sich für diese Ellipse
- [math] \begin{align*} a^2 - b^2 &= \left(\frac{p}{1-\varepsilon^2}\right)^2 - \left(\frac{p}{\sqrt{1 - \varepsilon^2}}\right)^2 \\ &= e^2 \enspace \enspace \enspace \enspace \text{(IV)} \end{align*}[/math]
Aus (I) und (II) ergibt sich
- [math] \frac{b^2}{a} = p \enspace \enspace \enspace \enspace \text{(V)}[/math]
Aus (III) ergibt sich
- [math] \varepsilon = \frac{e}{a} \enspace \enspace \enspace \enspace \text{(VI)}[/math]
Aus (V) und (VI) ergibt sich [math] r = \frac{b^2}{a - e \cdot \cos \left(\varphi \right)} \Leftrightarrow a - e \cdot \cos \left(\varphi \right) = \frac{b^2}{r} \Leftrightarrow e\cdot \cos \left(\varphi \right) = a - \frac{b^2}{r} \enspace \enspace \enspace \enspace \text{(VII)}[/math]
Der Abstand der beiden Brennpunkte, den wir zuvor mit [math]2 \cdot e[/math] angegeben haben, lässt sich nun als [math]r \cdot \cos \left(\varphi \right)[/math] und [math]2e - r \cdot \cos \left(\varphi \right)[/math] schreiben. Daraus ergibt sich nun eine Ellipse mit den Strecken [math]r[/math] und [math]s[/math]. Die beiden Dreiecke lassen sich mit Hilfe des Satzes von Pythagoras berechnen. Für das Dreieck mit der Hypotenuse [math]r[/math] gilt:
- [math] r^2 = (r\cdot \cos \left(\varphi \right))^2 + x^2 \Leftrightarrow x^2 = r^2 - r^2 \cdot \cos^2 \left(\varphi \right) \enspace \enspace \enspace \enspace \text{(VIII)}[/math]
Für das Dreieck mit der Hypotenuse [math]s[/math] gilt:
- [math] s^2 = x^2+(2 \cdot e-r \cdot \cos \left(\varphi \right))^2 [/math]
Nehmen wir nun diese Gleichung und wenden (VIII), (IV) und (VII) darauf an, so erhalten wir:
- [math] \begin{align*} s^2 & \stackrel{\hphantom{\text{(IV),(VII)}}}{=} x^2+(2 \cdot e-r \cdot \cos \left(\varphi \right))^2 \\ & \stackrel{\hphantom{\text{(.)}}\text{(VIII)}\hphantom{\text{(.)}}}{=} 4\cdot e^2-4\cdot e\cdot r\cdot \cos \left(\varphi \right)+r^2\\ & \stackrel{\text{(IV),(VII)}}{=} (2\cdot a-r)^2 \end{align*}[/math]
Somit ergibt dich die Gleichung
- [math] s=2\cdot a-r [/math]
und wir erhalten
- [math] r+s = r+2\cdot a -r = 2\cdot a \text{ ist konstant}[/math]
Hieraus folgt, da die Summe der Streckenlängen [math]r[/math] und [math]s[/math] konstant ist, dass sich der Körper der Definition nach auf einer Ellipse bewegt.
Zweites Keplersches Gesetz (Flächensatz)
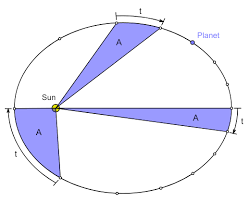
In gleichen Zeiten überstreicht der Fahrstrahl Objekt-Gravizentrum gleiche Flächen.
Der Fahrstrahl bildet die Verbindungslinie zwischen dem Schwerpunkt eines Himmelskörpers und dem Gravizentrum seiner Bewegung, dem Zentralkörper. Dies ergibt sich aus der Gravitationskraft, die entlang des Fahrstrahls wirkt und aus der Drehimpulserhaltung.
Herleitung
In der Zeit [math]\Delta t[/math] bewegt sich der Himmelskörper von Ort [math]r_1[/math] bis Ort [math]r_2[/math], hierbei überstreicht der Fahrstrahl eine Fläche [math]A[/math]. Diese Fläche besitzt bei ausreichend kleiner [math]\Delta t[/math] die Form eines Dreiecks, das von [math]r_1[/math], [math]r_2[/math] und dem Wegstück [math]s=v\cdot \Delta t[/math] begrenzt ist. Für die Fläche A gilt:
- [math] A=\frac{1}{2}\cdot r\cdot h \text{ mit } \sin\alpha = \frac{h}{s} \Leftrightarrow h=\sin\left(\alpha\right)\cdot v\cdot\Delta t,[/math]
wobei [math]\alpha[/math] der Winkel zwischen Radiusvektor und Geschwindigkeitsvektor ist. Daraus ergibt sich:
- [math] A=\frac{1}{2}\cdot r\cdot \sin\left(\alpha\right)\cdot v\cdot\Delta t[/math]
Da [math]\frac{1}{2}[/math] und [math]\Delta t[/math] gleich bleiben, lassen sie sich raus kürzen und es ergibt sich
- [math] A=r\cdot \sin\left(\alpha\right)\cdot v[/math]
Geschwindigkeitsverhältnis von Perihel und Aphel
Als Perizentrum und Apozentrum werden die beiden Brennpunkte des Baryzentrums bezeichnet, hierbei bildet die Sonne das Perizentrum. Die beiden Punkte, an der Himmelskörper den Brennpunkten am nächsten sind, bilden die Schnittpunkte der Umlaufbahn mit der Linie durch die beiden Brennpunkte. Hierbei bezeichnet Perihel den dem Perizentrum nächsten, sonnennächsten Punkt und Aphel den dem Apozentrum nächsten Punkt. Die Erde erreicht diese Punkte Anfang Januar (Prihel) mit ca. 147,1 Mio. km bzw. 0,983 AE und Anfang Juli (Aphel) mit ca. 152,1 Mio. km bzw. 1,017 AE Entfernung zur Sonne. Da das Produkt [math]r\cdot v\cdot\sin\left(\alpha\right)[/math] konstant ist und an den Punkten Perihel und Aphel [math]\alpha=90^\circ[/math], daraus folgt [math]sin\left(\alpha\right)=1[/math]. Somit stehen Perihel und Aphel in folgender Beziehung:
- [math]r_{Aphel}\cdot v_{Aphel}=r_{Perihel}\cdot v_{Perihel} \geq (a+e)\cdot v_{Aphel} = (a-e)\cdot v_{Perihel}[/math]
Der Zentalkörper und der Himmelskörper bilden ein geschlossenes System, in dem sich der Drehimpuls nicht ändern darf. Daraus ergibt sich, dass der Himmelskörper eine geringere Geschwindigkeit hat, wenn dieser weit weg vom Drehpunkt ist. Je näher er dem Drehpunkt kommt, desto größer ist seine Geschwindigkeit. Dem Drehimpulserhaltungssatz nach ist:
- [math] m\cdot v\cdot r\cdot \sin\left(\alpha\right)=\text{const.}[/math]
Wegen der konstanten Masse folgt
- [math] v\cdot r\cdot \sin\left(\alpha\right)=\text{const.}[/math]
Dies entspricht der überstrichenen Flächen im zweiten Keplerschen Gesetz.
- [math] A=r\cdot \sin\left(\alpha\right)\cdot v =\text{const.}[/math]
Folglich ist die überstrichene Fläche konstant.
Drittes Keplersches Gesetz
Die Quadrate der Umlaufzeiten stehen im gleichen Verhältnis wie die Kuben (dritten Potenzen) der großen Halbachsen, hierbei ist [math]T=\Delta t[/math]:
- [math] \left({\frac {T_{1}}{T_{2}}}\right)^{2}=\left({\frac {r_{1}}{r_{2}}}\right)^{3}[/math]
Herleitung
Aus dem Gravitationsgesetz lässt sich herleiten, dass für alle Planeten im Gravitationsfeld der Sonne der Quotient aus der dritten Potenz des Kreisradius und dem Quadrat der Umlaufzeit gleich groß und damit für das gesamte Planetensystem konstant ist. Entlang des Radius [math]r[/math] wirkt die Zentripetalkraft [math]F_Z[/math] des Zentralkörpers.
- [math] F_Z= F_G \Leftrightarrow m\cdot a_Z=G\cdot \frac{m\cdot M}{r^2}[/math]
Mit der Winkelgeschwindigkeit [math]\omega=\frac{v}{r} \Leftrightarrow v=r \cdot \omega[/math] ergibt sich:
- [math] \begin{align*} G\cdot \frac{m\cdot M}{r^2}&=m\cdot a_z\\ &=m\cdot \frac{v^2}{r}\\ &=m\cdot \frac{r^2\cdot \omega^2}{r}\\ &=m\cdot r\cdot \omega^2 \end{align*}[/math]
Aufgrund der konstanten Winkelgeschwindigkeit gilt:
- [math] \omega = \frac{2\pi}{T}[/math]
Damit ergibt sich:
- [math] m\cdot r \cdot \frac{4\pi^2}{T^2}=G\cdot \frac{m\cdot M}{r^2} \Leftrightarrow r\cdot \frac{4\pi^2}{T^2}=G\cdot \frac{M}{r^2} \Leftrightarrow \frac{r^3}{T^2}=G\cdot \frac{M}{4\pi^2}[/math]
Da nun [math]\frac{r^3}{T^2}=G\cdot \frac{M}{4\pi^2}[/math] nicht mehr abhängig von [math]m[/math] der Masse des bewegten Körpers ist, sondern nur noch von [math]M[/math] der Masse des Zentralkörpers, gilt für Planeten, die um den selben Zentralkörper bewegen (für die [math]M[/math] identisch ist):
- [math] \frac{r^3}{T^2}=\text{const.}[/math]
Daraus folgt:
- [math] \begin{align*} \frac{r_1^3}{T_1^2} &= \frac{r_2^3}{T_2^2}\\ T_1^2\cdot r_2^3 &= T_2^2\cdot r_1^3\\ \left({\frac {T_{1}}{T_{2}}}\right)^{2}&=\left({\frac {r_{1}}{r_{2}}}\right)^{3} \end{align*}[/math]
Das Zweikörperproblem
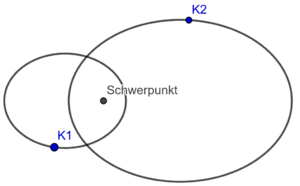
Mit dem Zweikörperproblem bezeichnet man die Frage nach der Bewegung zweier Körper, die sich gegenseitig gravitativ anziehen. Dieses lässt sich auf das Keplerproblem zurückführen, bei dem man die Bewegung eines einzelnen Körpers um eine zentrale Kraft betrachtet. Das Keplerproblem beschreibt somit einen idealisierten Fall, bei dem die Masse des sich bewegenden Körpers verglichen mit dem Zentralkörper vernachlässigbar ist, beispielsweise bei der Bewegung eines Satelliten um die Erde oder eines Planeten um die Sonne.
In dem Fall, dass beide Körper eine Kraft auf den jeweils anderen ausüben, lassen sich die Bewegungsgleichungen durch Koordinatentransformation entkoppeln, und man erhält für jeden Körper individuell ein Keplerproblem mit einer Zentralkraft im gemeinsamen Schwerpunkt. Die beiden Körper werden sich also gemäß dem ersten Keplerschen Gesetz jeweils auf einem Kegelschnitt (Ellipse, Parabel oder Hyperbel) mit dem Schwerpunkt in einem der Brennpunkte bewegen. Der Schwerpunkt selbst kann sich dabei gleichförmig bewegen, also mit konstanter Geschwindigkeit entlang einer Geraden.
Das Keplerproblem
Die Newtonsche Bewegungsgleichung für das Keplerproblem lautet
[math]\begin{align*} \ddot{\vec{r}} = \frac{-\mu}{r^2} \frac{\vec{r}}{r} \end{align*}[/math]
mit positiver reeller Konstante [math]\mu \gt 0[/math], Ortsvektor des Körpers [math]\vec{r}[/math] und dessen Betrag [math]r[/math]. Die Zentralkraft befindet sich im Ursprung. Diese Gleichung lässt sich aus dem Newtonschen Gravitationsgesetz [math]\begin{align*}-\vec{F} = \frac{Gm_1m_2}{r^3}\vec{r}\end{align*}[/math]
mit Massen [math]m_1, m_2[/math] der beiden Körper herleiten, indem man das Kraftgesetz [math]\begin{align*}F = m_2\ddot{\vec{r}}\end{align*}[/math] für einen der Körper einsetzt. Dadurch kürzt sich eine der Massen und man erhält [math]\mu = m_1G[/math], mit Gravitationskonstante [math]G[/math].
Das erste Keplersche Gesetz besagt, dass die Bahn des Körpers [math]\vec{r}[/math] eine Ellipse ist. Dies ist aber noch keine Lösung des Keplerproblems. Gesucht ist eine zwei mal stetig differenzierbare Funktion [math]\vec{r}(t)[/math], welche obige Differentialgleichung löst und damit die Position des Körpers zu jedem Zeitpunkt [math]t \in \mathbb{R}[/math] angibt. Die lokale Existenz und Eindeutigkeit einer solchen Lösung ist für jeden Anfangswert durch den Satz von Picard-Lindelöf gesichert. Die globale Existenz zeigt man durch ein Fortsetzungsargument[1].
Zur Beschreibung der Lösung betrachten wir eine Ellipse mit großer Halbachse [math]a[/math], kleiner Halbachse [math]b[/math] und Exzentrizität [math]e[/math]. Wählt man das Koordinatensystem derart, dass der Exzentrizitätsvektor auf der positiven x-Achse liegt, dann hat ein Punkt [math]r[/math] auf der Ellipse die Koordinaten
[math]r = \frac{a(1-e^2)}{1+e\cdot cos(\varphi)}\cdot\left( \begin{array}{c} cos(\varphi)\\ sin(\varphi)\\ \end{array} \right) [/math],
wobei [math]\varphi[/math] der Winkel zwischen [math]x[/math]-Achse und Ortsvektor ist. Man kann also [math]\vec{r}(t)[/math] auch als Funktion von [math]\varphi (t)[/math] schreiben, und erhält
[math]\vec{r}(\varphi(t)) = \frac{a(1-e^2)}{1+e\cdot cos(\varphi(t))}\cdot\left( \begin{array}{c} cos(\varphi(t))\\ sin(\varphi(t))\\ \end{array} \right) [/math]
Man wähle das Koordinatensystem so, dass der Mittelpunkt der Ellipse [math]Z \in \mathbb{R}[/math] auf der x-Achse liegt und zeichne um diesen einen Kreis mit Radius [math]a[/math]. Auf diesem Kreis findet man zu jedem Punkt [math]r[/math] der Ellipse den eindeutigen entsprechenden Punkt [math]R[/math] mit der selben x-Koordinate, wie in der Grafik dargestellt. Den Winkel [math]u[/math] zwischen [math]x[/math] -Achse und dem Ortsvektor von [math]R[/math] nennt man exzentrische Anomalie von [math]r[/math]. Zum Perizentrum der Ellipse gehört also z.B. die exzentrische Anomalie [math]2 \pi z, z \in \mathbb{Z}[/math].
Schreibt man den Punkt [math]r[/math] auf der Ellipse in Abhängigkeit seiner exzentrischen Anomalie [math]u[/math], so erhält man als Koordinaten [math]r = a\left( \begin{array}{c} cos(u)-e\\ \sqrt{1-e^2}sin(u)\\ \end{array} \right) [/math]
Man beachte hierzu, dass der entsprechende Punkt [math]R[/math] auf dem Kreis die Koordinaten [math]R = \left( \begin{array}{c} a \cdot cos(u)+Z\\ a \cdot sin(u)\\ \end{array} \right) [/math] besitzt. Da die Exzentrizität durch [math]e = \frac{-Z}{a}[/math] definiert ist, gilt [math]R = \left( \begin{array}{c} a \cdot cos(u)-ea\\ a \cdot sin(u)\\ \end{array} \right) [/math]
[math]r[/math] besitzt die selbe [math]x[/math]-Koordinate wie [math]R[/math]. Die [math]y[/math]-Koordinate erhält man durch den Vergleich der Parametrisierungen des Kreises und der Ellipse mit Mittelpunkt [math]-Z = ea[/math] und Radius bzw. große Halbachse [math]a[/math]. Der Kreis ist gegeben durch [math]\frac{(x+ea)^2}{a^2}+\frac{y^2}{a^2} = 1[/math] und die Ellipse durch [math]\frac{(x+ea)^2}{a^2}+\frac{y^2}{b^2}=1[/math]. Da die [math]x[/math]-Koordinaten von [math]r[/math] und [math]R[/math] übereinstimmen und daher die [math]x[/math]-Terme eliminiert werden können, liefert Gleichsetzen das Verhältnis [math]y_r = \frac{b}{a}y_R[/math]. In einer Ellipse gilt das Verhältnis [math]b = a\sqrt{1-e^2}[/math] zwischen den Halbachsen. Also [math]y_r = b\cdot sin(u) = a\cdot\sqrt{1-e^2}\cdot sin(u)[/math].
Lösung des Keplerproblems
Die Lösung des Keplerproblems [math]\vec{r}(t)[/math] mit
- Energie des Systems [math]\lt 0[/math] (das entspricht einer Ellipsenbahn)
- Drehimpuls ungleich 0
- großer Halbachse [math]a[/math]
- Startposition des Körpers zum Zeitpunkt [math]t_0[/math] im Perizentrum
ist gegeben durch
[math]\vec{r}(t) = a\left( \begin{array}{c} cos(u(t))-e\\ \sqrt{1-e^2}sin(u(t))\\ \end{array} \right) [/math]
wobei [math]u(t)[/math] die eindeutige Lösung der Keplergleichung
[math]u(t) - e\cdot sin(u(t)) = \frac{2\pi}{p}(t-t_0)[/math] ist.
[math]p[/math] ist hierbei die Periode, die durch das dritte Keplersche Gesetz festgelegt ist. Die Keplergleichung lässt sich nicht explizit nach [math]u(t)[/math] auflösen, daher liegt die Lösung des Keplerproblems nur implizit vor.
Beweis
Sei [math]r(t)[/math] eine Lösung des Keplerproblems. In vorigem Abschnitt wurde
[math]\vec{r}(t) = a\left( \begin{array}{c} cos(u(t))-e\\ \sqrt{1-e^2}sin(u(t))\\ \end{array} \right) [/math] hergeleitet. Es bleibt zu zeigen, dass [math]u(t)[/math] die Keplergleichung erfüllt. Es gilt [math]\dot{\vec{r}} = a\left( \begin{array}{c} -\dot u sin(u)\\ \sqrt{1-e^2}\dot u cos(u)\\ \end{array} \right) [/math].
Fasst man [math]\vec{r}[/math] und [math]\dot{\vec{r}}[/math] als Vektoren in [math]\mathbb{R}^3[/math] auf, so errechnet sich der Drehimpuls als [math]\vec{r} \times \dot{\vec{r}} = \left( \begin{array}{c} 0\\ 0\\ c\\ \end{array} \right)[/math] mit [math]c = a^2 \sqrt{1-e^2} \dot u (1-ecos(u))[/math]
Für Lösungen des Keplerproblems gilt der Zusammenhang [math]\mu ^2 (e^2-1) = 2 E_ges c^2[/math] zwischen Exzentrizität [math]e[/math] des Kegelschnitts und Gesamtenergie [math]E_ges[/math] des Systems[2]. Auflösen nach [math]c[/math] und Gleichsetzen der beiden Ausdrücke liefert [math]\dot u = \frac{\sqrt{\mu}}{a^{3/2}} \cdot \frac{1}{1-e \cdot cos(u)} \gt 0[/math], da [math]e\lt 1[/math] nach Definition. [math]u[/math] ist also streng monoton steigend, und daher ein Diffeomorphismus. Es exisitiert somit ein eindeutiger Zeitpunkt [math]t_0 \in \mathbb{R}[/math] mit [math]u(t_0) = 0[/math], was bedeutet, dass der Körper sich zu diesem Zeitpunkt im Perizentrum [math]\vec{r}(t_0) = \left( \begin{array}{c} a(1-e)\\ 0\\ \end{array} \right)[/math] befindet.
Durch Umstellen der Gleichung [math]\dot u = \frac{\sqrt{\mu}}{a^{3/2}} \cdot \frac{1}{1-e \cdot cos(u)}[/math] zu
[math]\dot u (1-ecos(u)) = \frac{\sqrt{\mu}}{a^{3/2}}[/math]
und Integrieren beider Seiten, erhält man:
[math]u(t) - esin(u(t)) = \frac{\sqrt{\mu}}{a^{3/2}}(t-t_0)[/math]
Für die exzentrische Anomalie [math]u[/math] und die Periode [math]p[/math] gilt nach Definition [math]u(t_0+p) = 2\pi[/math]. Setzt man also [math]t = t_0+p[/math] ein, erhält man
[math]2\pi - esin(2\pi) = \frac{\sqrt{\mu}}{a^{3/2}}p[/math],
also [math]\frac{\sqrt{\mu}}{a^{3/2}} = \frac{2\pi}{p}[/math] und daher die Keplergleichung. Dass die Lösung der Keplergleichung eindeutig ist, folgt aus dem Satz von der impliziten Funktion.
Umformung des Zweikörperproblems
Man betrachte nun zwei Körper mit Massen [math]m_1[/math] und [math]m_2[/math] und Ortsvektoren [math]\vec{r_1}[/math] und [math]\vec{r_2}[/math]. Nach dem Gravitationsgesetz gelten die Bewegungsgleichungen
[math]\ddot{\vec{r_1}} = Gm_2\frac{\vec{r_2}-\vec{r_1}}{|r_2 - r_1|^3} \enspace \enspace \text{(I)} \\ \ddot{\vec{r_2}} = Gm_1\frac{\vec{r_1}-\vec{r_2}}{|r_1 - r_2|^3} \enspace \enspace \text{(II)} [/math]
Relative Koordinaten
Eine Möglichkeit das Zweikörperproblem zu lösen, ist es eine Gleichung für den Abstand [math]\vec{r}:=\vec{r_2}-\vec{r_1}[/math] aufzustellen. Zieht man die erste Bewegungsgleichung [math] \text{(I)} [/math] von der zweiten [math] \text{(II)} [/math] ab, dann bekommt man
[math]\ddot{\vec{r}} = -G(m_1+m_2)\cdot \frac{\vec{r}}{r^3}[/math]
Das ist das Keplerproblem mit Konstante [math]\mu = G(m_1+m_2)[/math]. Die Lösung [math]\vec{r}(t)[/math] ist also bekannt. Ersetzt man den Term [math]\vec{r_2}-\vec{r_1}[/math] auf der rechten Seite der ersten Gleichung [math] \text{(I)} [/math] durch die bekannte Lösung [math]\vec{r}[/math], so stellt man fest, dass die rechte Seite nicht mehr von [math]\vec{r_1} [/math] oder [math]\vec{r_2} [/math] abhängig ist. Insbesondere ist die zweite Ableitung von [math]\vec{r_1}[/math] aus [math] \text{(I)} [/math] schon bekannt, also kann man beide Seiten zweimal integrieren und erhält für die Lösung [math]\vec{r_1(t)} + c \cdot t + d[/math] mit Integrationskonstanten [math]c[/math] und [math]d[/math]. Diese lassen sich aus den gewählten Anfangswerten [math]\vec{r_1}(t_0)[/math], [math]\dot{\vec{r_1}}(t_0)[/math], [math]\vec{r_2}(t_0)[/math], [math]\dot{\vec{r_2}}(t_0)[/math] bestimmen.
Mit der Umschreibung [math]\vec{r_2(t)} = \vec{r}(t)+\vec{r_1(t)}[/math], wobei [math] \vec{r} [/math] und [math] \vec{r_1} [/math] aus dem letzten Schritt bekannt sind, lässt sich auch [math]\vec{r_2}[/math] bestimmen.
Quellen
- https://astrokramkiste.de/heliozentrisches-weltbild/kopernikanisches-weltbild (letzter Zugriff 17.09.2021)
- https://www.leifiphysik.de/mechanik/weltbilder-keplersche-gesetze/ausblick/herleitung-des-ersten-keplerschen-gesetzes (letzter Zugriff 17.09.2021)
- https://de.wikipedia.org/wiki/Keplersche_Gesetze (letzter Zugriff 17.09.2021)
- https://www.leifiphysik.de/astronomie/planetensystem/grundwissen/zweites-keplersches-gesetz-fortfuehrung (letzter Zugriff 17.09.2021)
- https://physikbuch.schule/keplers-laws-of-planetary-motion.html (letzter Zugriff 17.09.2021)
- https://www.timeanddate.de/astronomie/perihel-aphel-sonne (letzter Zugriff 10.09.2021)
- https://www.leifiphysik.de/mechanik/gravitationsgesetz-und-feld/aufgabe/herleitung-des-3-keplerschen-gesetzes-fuer-kreisbahnen (letzter Zugriff 17.09.2021)
- https://www.cambridge.org/core/journals/british-journal-for-the-history-of-science/article/abs/keplers-laws-of-planetary-motion-16091666/699210848492633F05BA8C2BC2790EF2 (letzter Zugriff 18.09.2021)
- https://www.jstor.org/stable/24927297 (letzter Zugriff 18.09.2021)
- Hansjörg Geiges - The geometry of celestial mechanics, Kapitel 1-5
Einzelnachweise
Autoren
- Koralie Pietsch
- Yordan Mitev
- Leonardo Valle