Fourieranalyse

Aus FunFacts Wiki
Zur Navigation springen Zur Suche springen

Die Fourier Reihe, bzw. die Fourier Transformation ist ein wichtiges Werkzeug der modernen Mathematik, Physik und Signalanalyse, und hat somit große praktische Bedeutung. Eine Fourierreihe ist eine Darstellung einer periodischen Funktion als Reihe von Sinus- und Kosinusschwingungen verschiedener Frequenzen. Die Fourier Transformation ist eine Verallgemeinerung hiervon; sie bildet auch aperiodische Funktionen auf ein Frequenzspektrum ab, bildlich gesprochen "wie viel von einer Frequenz in der Funktion vor kommt".

Ein klassisches Beispiel ist die Kompression von Audiodateien, beispielsweise MP3: Hierbei wird das gegebene Signal per Fouriertransformation in die einzelnen Frequenzen aufgespalten, sowieso nicht für Menschen hörbare, aber trotzdem vorhandene Frequenzen, werden gelöscht, und das ganze wird zu einer erheblich kleineren Datei rücktransformiert.

Fourier-Reihen

Summendarstellung

Wir betrachten zunächst eine bezüglich des Intervalls [math] [ - \pi, \pi][/math] [math]2 \pi[/math]-periodische, abschnittsweise stetige und integrierbare Funktion [math]f[/math].

Die Fourier-Reihe zu dieser Funktion [math] f[/math] ist eine Reihendarstellung aus komplexwertiger [math]e[/math]-Funktionen:

[math] \displaystyle FS(f) = \sum_{k \in \mathbb{Z}} c_k e^{ikx}~, c_k \in \mathbb{C}[/math]

Dies lässt sich auch umschreiben:

[math] \displaystyle FS(f) = \sum_{k = -\infty} ^ \infty c_k e^{ikx} = c_0 + \sum_{k = 1} ^\infty (c_k + c_{-k}) \cos (kx) + i(c_k - c_{-k}) \sin (kx) := \frac{a_0}{2} + \sum_{k = 1}^\infty a_k \cos (kx) + b_k \sin (kx) [/math]

mit [math] a_k = c_k + c_{-k} [/math], [math] b_k = i(c_k - c_{-k}) [/math] und insbesondere [math] a_0 = 2c_0 [/math]. Es ist ersichtlich, dass die [math]2\pi[/math]-periodische Funkion [math]f[/math] als gewichtete Summe aller [math]2\pi[/math]-periodischen Sinus und Kosinus dargestellt wird.

Berechnung der Koeffizienten

Ist eine Funktion [math]f[/math] gegeben, so müssen nur die Koeffizienten [math]c_k[/math] bestimmt werden. Hierfür ist folgende Beobachtung essenziell, für [math]k \neq 0[/math]:

[math] \displaystyle \int_{-\pi}^ \pi e^{ikx} \text{d}x = \int_{-\pi}^{\pi} \cos (kx) \text{d}x + i \int_{-\pi}^{\pi} \sin (kx) \text{d}x = Big[- \frac{1}{m} \sin (kx) \Big]_{-\pi}^\pi + \Big[ i \frac{1}{m} \cos (kx) \Big]_{-\pi}^{\pi} = 0 [/math]

Für [math]k = 0[/math] ist das Integral trivialerweise 1. Somit gilt der Zusammenhang

[math] \displaystyle \int_{-\pi}^\pi f(x) \text{d}x = \int_{-\pi}^\pi \sum_{k \in \mathbb{Z}} c_k e^{ikx} \text{d}x = \sum_{k \in \mathbb{Z}} \int_{-\pi}^\pi c_k e^{ikx} \text{d}x = c_0 [/math]

und

[math] \displaystyle \int_{-\pi}^\pi f(x)\cdot e^{-inx} \text{d}x = \sum_{k \in \mathbb{Z}} \int_{-\pi}^\pi c_k e^{i(k-n) x} \text{d}x = c_n [/math]


Konvergenz einer Reihendarstellung

Um uns mit der Konvergenz einer Fourier-Reihe zu einer gegebenen Funktion zu befassen, definieren wir zunächst für ein [math] \: f: \mathbb{R} \rightarrow \mathbb{C} [/math] und ein [math] x \in \mathbb{R} [/math] im Fall der Existenz der jeweiligen Limiten

[math] f( x^+) := \lim_{t \searrow x} f(t) \: \: \: \: \: \: f( x^-) := \lim_{t \nearrow x} f(t) \: \: \: \: \: \: f(x^+_-) := \frac{f( x_+) + f( x^-)}{2} \\ f´( x^+) := \lim_{t \searrow 0} \frac{f(x+t)-f(x)}{t} \\ f´( x^-) := \lim_{t \nearrow 0} \frac{f(x+t)-f(x)}{t} [/math]

Nun können wir die zentrale Aussage dieses Abschnitts formulieren:

Konvergenzsatz von Dirichlet

Sei [math] \, f: \mathbb{R} \rightarrow \mathbb{R} \; 2\pi[/math]-periodisch und integrierbar auf [math] [ 0, 2π ] [/math]. Sei [math] x  \in  \mathbb{R} [/math] derart, dass [math] \, f( x^+), \, f( x^-), \, f´(x^+) \, [/math] und [math] \, f´(x^−) \, [/math] existieren. Dann gilt [math] \, FS(f)(x) = f(x^+_-) [/math].


Insbesondere gilt also, falls [math] \, f \, [/math] in [math]\, x \, [/math] differenzierbar ist, [math] \, FS(f)(x) = f(x) [/math].

Beweis:  
Wir definieren zunächst:

Für alle [math] n \in \mathbb{N} [/math] heiße die Funktion [math] D_n: \mathbb{R} \rightarrow \mathbb{C}, \; x \mapsto \sum_{k=-n}^n e^{ikx} \\ [/math] der n-te Dirichlet-Kern.

Bevor wir mit dem eigentlichen Beweis des Satzes beginnen, lagern wir einige Aussagen in Hilfssätze aus:

Lemma 1: (Sinusdarstellung der Dirichlet-Kerne)

Für alle [math] n \in \mathbb{N} [/math] und alle [math] x  \in  \mathbb{R} \setminus \{ 2\pi a \, |\, a  \in  \mathbb{Z} \} [/math] gilt

[math] D_n(x)  = \frac{\sin(n x + \frac{x}{2})}{\sin(\frac{x}{2})} [/math].

Weiter ist [math] D_n(2 \pi a)  =  2n + 1 [/math]  für alle [math] \; a  \in \mathbb{Z} [/math].


Beweis:

Sei [math] x \in \mathbb{R} \setminus \{ 2 \pi a | a \in \mathbb{Z} \} [/math]. Dann gilt

[math] D_n(x) = \sum_{k=-n}^n e^{ikx} = e^{-inx} \sum_{k=0}^{2n} e^{ikx} [/math].

Da gilt [math] e^{inx} \neq 1 [/math], folgern wir aus der Formel der Partialsummen einer geometrischen Reihe

[math] \begin{align} D_n &= e^{-inx} \frac{1-e^{i(2n+1)x}}{1-e^{ix}} \\ \\ &= \frac{e^{-inx}e^{-\frac{x}{2}}}{e^{-\frac{x}{2}}} \frac{e^{i(2n+1)x}-1}{e^{ix}} \\ \\ &= \frac{e^{i (n + \frac{1}{2}) x} − e^{−i (n + \frac{1}{2}) x}}{e^{\frac{i x}{2}} − e^{− i \frac{x}{2}}} \end{align} [/math]

Nun folgern wir aus der Euler-Formel für beliebige [math] \varphi \in \mathbb{R} : \; e^{i \varphi} - e^{-i \varphi} = 2i \sin(\varphi) [/math]. Damit gilt

[math] D_n(x) = \frac{\sin(nx + \frac{x}{2})}{\sin(\frac{x}{2})} [/math].

Des weiteren gilt für alle [math] a \in \mathbb{Z}: \; D_n(a2 \pi) = \sum_{k=-n}^{n}1 = 2n+1 [/math].


Lemma 2:

Sei [math] \, f: \mathbb{R} \rightarrow \mathbb{C} \; 2 \pi [/math]-periodisch und integrierbar. Dann gilt für alle [math] n \in \mathbb{N}, \; x \in \mathbb{R} [/math]

[math] \begin{align} FS_n(f)(x) &= \frac{1}{2 \pi} \int_{0}^{2 \pi} f(t) D_n(x-t) \, dt \\ &= \frac{1}{2 \pi} \int_{0}^{2 \pi} f(x-t) D_n(t) \, dt = \frac{1}{2 \pi} \int_{0}^{2 \pi} f(x+t) D_n(t) \, dt \end{align} [/math]


Beweis:

Sei [math] n \in \mathbb{N} [/math], dann gilt für alle [math] x \in \mathbb{R} [/math] laut der Formel für die Koeffizienten einer Fourier-Reihe

[math] \begin{align} FS_n(f)(x) &= \frac{1}{2 \pi} \sum_{k=-n}^{n} \int_{0}^{2 \pi} f(t)e^{-ikx} \, dt \; e^{ikx} \\ &= \frac{1}{2 \pi} \int_{0}^{2 \pi} f(t) \sum_{k=-n}^{n} e^{ik(t-x)} \, dt \\ &= \frac{1}{2 \pi} \int_{0}^{2 \pi} f(t) D_n(x-t) \end{align} [/math].

Des weiteren können wir durch die Substitutionsregel mit [math] "t=x-y" [/math] folgern

[math] \frac{1}{2 \pi} \int_{0}^{2 \pi} f(t) D_n(x-t) = \frac{1}{2 \pi} \int_{x}^{x-2 \pi} -f(x-y) D_n(y) \, dy [/math]

Da [math] \, f [/math] und [math] D_n \; 2\pi[/math]-periodisch sind, gilt somit

[math] \frac{1}{2 \pi} \int_{0}^{2 \pi} f(t) D_n(x-t) = \frac{1}{2 \pi} \int_{x}^{x-2 \pi} -f(x-y) D_n(y) \, dy = \frac{1}{2 \pi} \int_{0}^{2 \pi} f(x-t) D_n(t) \, dt [/math].

Analog zeigt man durch Substitution mit [math] t=x+y [/math] unter Verwendung von [math] D_n(-t) = D_n(t) [/math], dass gilt

[math] \frac{1}{2 \pi} \int_{0}^{2 \pi} f(t) D_n(x-t) = \frac{1}{2 \pi} \int_{0}^{2 \pi} f(x+t) D_n(t) \, dt [/math].


Lemma 3: (Lemma von Riemann)

Sei [math] \, f: [a,b] \rightarrow \mathbb{C} [/math] integrierbar. Dann gilt

[math] \lim_{\lambda \rightarrow \infty} \int_a^b f(x) sin(\lambda x) \, dx = \lim_{\lambda \rightarrow \infty} \int_a^b f(x) cos(\lambda x) \, dx = 0 [/math]

Selbiges gilt für [math] "\lambda \rightarrow -\infty" [/math]


Beweis: Wir wollen das Lemma durch das [math] \varepsilon [/math]-[math] \delta [/math]-Kriterium beweisen. Dazu zeigen wir die Aussage zuerst für Treppenfunktionen. Sei dazu [math] (t_k)_{t \leq r} [/math] eine Partition von [math] [a,b] [/math] aufsteigende Folge mit [math] t_0 = a, \; t_r=b, \; c_k \in \mathbb{C} [/math] für alle [math] k \lt r [/math] und [math] g: [a,b] \rightarrow \mathbb{C} [/math] gegeben durch [math] g(x):=c_k [/math] für [math] t_k \leq x \lt t_k+1 [/math]. Nun gilt für [math] \lambda \in \mathbb{R} \setminus \{ 0 \} [/math]

[math] \begin{align} \Bigl| \int_a^b g(x) sin(\lambda x) \, dx \Bigl| &= \Bigl| \sum_{k=0}^{r-1} \int_{t_k}^{t_{k+1}} g(x) sin(\lambda x) \, dx \Bigl| \\ &= \Bigl| \sum_{k=0}^{r-1} c_k \int_{t_k}^{t_{k+1}} sin(\lambda x) \, dx \Bigl| \\ &= \Bigl| \sum_{k=0}^{r-1} c_k \Bigl[\frac {cos(\lambda x)}{\lambda} \Bigl]_{t_k}^{t_{k+1}} \, dx \Bigl| \\ &\leq \frac{2}{n} \Bigl| \sum_{k=1}^{r} c_k \Bigl|. \end{align} \\ \\ \Rightarrow \int_a^b g(x) sin(\lambda x) \, dx \overset{\lambda \rightarrow \infty}{\longrightarrow} 0 [/math]


Nun gilt nun Sei [math] \, f: [a,b] \rightarrow \mathbb{C} [/math] integrierbar und [math] \varepsilon \gt 0 [/math]. Dann existiert eine Treppenfunktion g, so dass gilt

[math] \Bigl| \int_a^b f(x)-g(x) \, dx \Bigl| \lt \frac{\varepsilon}{2} [/math]. (Die Integrierbarkeit von [math] \, f [/math] impliziert dessen Aproximierbarkeit durch Treppenfunktionen)

Sei nun [math] N \in \mathbb{N} [/math] so gewählt, dass für alle [math] n \in \mathbb{N} [/math] gilt [math] n\gt N \Rightarrow \Bigl| \int_a^b g(x) sin(nx) \, dx \Bigl| \lt \frac{\varepsilon}{2} [/math]. Dann gilt für alle [math] n \gt N [/math]

[math] \begin{align} \Bigl| \int_a^b f(x) sin(nx) \, dx \Bigl| &= \Bigl| \int_a^b (f(x)-g(x)) sin(nx) \, dx + \int_a^b g(x) sin(nx) \, dx \Bigl| \\ &\leq \Bigl| \int_a^b (f(x)-g(x)) sin(nx) \, dx \Bigl| + \Bigl| \int_a^b g(x) sin(nx) \, dx \Bigl| \\ &\leq \Bigl| \int_a^b (f(x)-g(x)) \, dx \Bigl| + \Bigl| \int_a^b g(x) sin(nx) \, dx \Bigl| \lt \frac{\varepsilon}{2} + \frac{\varepsilon}{2} = \varepsilon \end{align} [/math]


Nun können wir zu dem eigentlichen Beweis unseres Satzes schreiten. Zuerst stellen wir fest

[math] \int_{- \pi}^{\pi} D_n(x) \, dx = \sum_{k=-n}^{n} \int_{- \pi}^{\pi} e^{ikx} \, dx = \int_{- \pi}^{\pi} e^{i0x} \, dx = 2\pi [/math].

Da nach der Sinusdarstellung der Dirichlet-Kerne gilt [math] D_n(x) = \frac{\sin(n x + \frac{x}{2})}{\sin(\frac{x}{2})} = \frac{-\sin(-n x - \frac{x}{2})}{-\sin(-\frac{x}{2})} = \frac{\sin(-n x - \frac{x}{2})}{\sin(-\frac{x}{2})} = D_n(-x) [/math], können wir folgern

[math] \int_{- \pi}^{0} D_n(x) \, dx =\int_{0}^{\pi} D_n(x) \, dx = \pi [/math]

Damit gilt [math] \; f(x^+_-) = \frac{1}{2 \pi} \int_{- \pi}^{0} f(x^+) D_n(x) \, dx + \frac{1}{2 \pi} \int_{0}^{\pi} f(x^-)D_n(x) \, dx. [/math]

Unter Zuhilfenahme von Lemma 2 folgern wir

[math] 2\pi \Bigl|FS_n(f)(x) − f (x^+_-)\Bigl|  =  \Bigl| \int_{- \pi}^{0} (f (x + t) − f (x^-)) Dn(t) \, dt  +  \int_{0}^{\pi} (f (x + t) − f (x^+)) Dn(t) \, dt \Bigl| [/math].


Nun definieren wir [math] g_-: [- \pi, 0] \rightarrow \mathbb{C} \; g_+: [0, \pi] \rightarrow \mathbb{C} [/math] durch


[math] g_-(t):=\frac{f(x+t)-f(x^-)}{t}\frac{t}{sin(\frac{t}{2})} [/math] für [math] t \in [- \pi, 0) [/math]

[math] g_+(t):=\frac{f(x+t)-f(x^+)}{t}\frac{t}{sin(\frac{t}{2})} [/math] für [math] t \in (0, \pi] [/math]

Des weiteren sei [math] g_-(0):= \lim_{t \searrow 0} \frac{f(x+t)-f(x^-)}{sin(\frac{t}{2})}, \; \lim_{t \nearrow 0} \frac{f(x+t)-f(x^-)}{sin(\frac{t}{2})} [/math] (Da laut Annahme [math] f´(x^-), \, f´(x^+) [/math] existieren und [math] \frac{d}{dt} \Bigl(sin(\frac{t}{2})\Bigl)(0) = \frac{1}{2} \neq 0 [/math] gilt, gibt es die entsprechenden Limiten)

Nun können wir die Sinusdarstellung der Dirichlet-Kerne in die obige Formel einsetzen und erhalten

[math] 2\pi \Bigl|FS_n(f)(x) − f (x^+_-)\Bigl| = \Bigl| \int_{- \pi}^{0} g_- sin((n + \frac{1}{2})t) \, dt  +  \int_{0}^{\pi} g_+ sin((n + \frac{1}{2})t) \, dt \Bigl| [/math]. (Zwar gilt [math] (f (x + t) − f (x^-)) Dn(t) = g_- sin((n + \frac{1}{2})t) [/math] und [math] (f (x + t) − f (x^+)) Dn(t)=g_+ sin((n + \frac{1}{2})t) [/math] lediglich für alle [math] t \in \mathbb{R} \setminus \{ 2\pi a \, |\, a  \in  \mathbb{Z} \} [/math], das reicht aber aus, um die Gleichheit der jeweiligen Integrale zu gewährleisten)


[math] g_-, \, g_+ [/math] sind nach ihrer Konstruktion stetig und damit integrierbar. Damit können wir das Lemma von Riemann anwenden und schließen:

[math] 2\pi \Bigl|FS_n(f)(x) − f (x^+_-)\Bigl| \; \overset{n \rightarrow \infty}{\longrightarrow} \; 0 \\ \Rightarrow FS(f)(x) = f(x^+_-) [/math]

Beispiele

Beispiel 1:

Sei [math] \, f: \mathbb{R} \rightarrow \mathbb{R} \; 2 \pi [/math]-periodisch und auf [math] [0, 2 \pi) [/math] gegeben durch

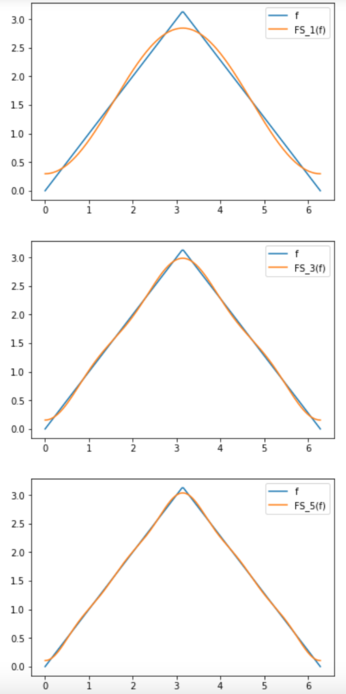
[math] f(x):= \begin{cases} x, \; 0 \leq x \leq \pi \\ \\ 2\pi - x, \pi \lt x \lt 2 \pi\; \end{cases} [/math]


Da [math] \, f [/math] stetig ist und für alle [math] x \in \mathbb{R} \; \; f´(x^-), \, f´(x^+) [/math] existieren, gilt nach dem Satz von Dirichlet [math] \, f=FS(f) [/math]. Im folgenden berechnen wir, wie oben beschrieben, die Koeffizienten dieser Fourier-Reihe:

[math] \begin{align} a_0 &= \frac{1}{\pi} \int_0^{2\pi} f(x) \, dx \\ &= \frac{2}{\pi} \int_0^{\pi} x \, dx = \frac{2 \pi^2 }{ 2 \pi} = \pi \end{align} [/math]

Approximationen von [math] \, f [/math] durch Partialsummen von [math] FS(f) [/math] auf dem Intervall [math] [0, 2 \pi] [/math]


Sei nun [math] n \in \mathbb{R} [/math], dann gilt

[math] \begin{align} a_n &= \frac{1} {\pi} \int_0^{2\pi} f(x) cos(nx) \, dx \\ &= \frac{1} {\pi} \Bigl( \int_0^{\pi} xcos(nx) \, dx + \int_{\pi}^{2\pi} 2\pi cos(nx) \, dx - \int_{\pi}^{2\pi} xcos(nx) \, dx \Bigl) \\ &= \frac{1} {\pi} \Bigl( 2\int_0^{\pi} xcos(nx) \, dx + \int_{\pi}^{2\pi} 2\pi cos(nx) \, dx \Bigl)\\ &= \frac{1} {\pi} \Bigl(2\int_0^{\pi} xcos(nx) \, dx + \Bigl[ \frac{2\pi}{n} sin(nx) \Bigl]_{\pi}^{2\pi} \Bigl)\\ &= \frac{1} {\pi} \Bigl( 2\int_0^{\pi} xcos(nx) \, dx + 0 \Bigl) \end{align} [/math].


Weiter können wir durch partielle Integration berechnen:

[math] \begin{align} a_n &= \frac{2}{\pi} \Bigl( \Bigl[\frac{x}{n} sin(nx) \Bigl]_{0}^{\pi} - \int_0^{\pi} \frac{1}{n} sin(nx) \, dx \Bigl) \\ \\ &= \frac{2}{\pi} \Bigl( 0 - \Bigl[ \frac{1}{n} cos(nx) \Bigl]_{0}^{\pi} \Bigl) \\ \\ &= -\frac{2}{\pi} \Bigl[\frac{1}{n^2} cos(nx) \Bigl]_{0}^{\pi} \\ \\ &= \begin{cases} 0, \; \text{falls}\, n \, \text{gerade ist} \\ \\ -\frac{4}{\pi n^2}, \; \text{falls}\, n \, \text{ungerade ist} \end{cases} \end{align} [/math]


Des weiteren gilt:

[math] \begin{align} b_n &= \frac{1} {\pi} \int_0^{2\pi} f(x) sin(nx) \, dx \\ \\ &= \frac{1} {\pi} \Bigl( \int_0^{\pi} f(x) sin(nx) \, dx + \int_{\pi}^{2\pi} f(x) sin(nx) \, dx \Bigl) \end{align} [/math].


Da aber für alle [math] \, x \in [0,\pi] [/math] gilt, [math] f(x)sin(x) = -f(x + \pi)sin(x+\pi) [/math] können wir daraus folgern [math] b_n = 0 [/math].


Damit gilt

[math] f(x) = FS(f)(x) = \frac{\pi}{2} - \frac{4}{\pi} cos(x) - \frac{4}{9\pi} cos(3x) - \frac{4}{25\pi} cos(5x) - \frac{4}{49\pi} cos(7x) \dots [/math].


Außerdem können stellen wir fest, dass für alle [math] \, n \in \mathbb{N} [/math] gilt

[math] \sum_{k = 0}^{n} |a_k| \leq \frac{\pi}{2} + \frac{4}{\pi} \sum_{k = 0}^{n} \frac{1}{k^2} [/math].


Da die verallgemeinerte geometrische Reihe [math] \sum_{k = 0}^{\infty} \frac{1}{k^\alpha} [/math] für [math] \alpha = 2 [/math] konvergiert, tut dies auch [math] \sum_{k = 0}^{\infty} |a_k| [/math]. Des weiteren gilt für alle [math] \, n \in \mathbb{N} [/math]

[math] \max_{x \in \mathbb{R}} |cos(nx)| = 1 [/math].

und wir können abschätzen:

[math] \sup_{x \in \mathbb{R}} |FS_n(f)(x) - f(x)| \leq \sum_{k = n + 1}^{\infty} |a_k| [/math]

Somit konvergiert die Fourier-Reihe zu [math] \, f [/math] nicht nur punktweise, wie es der Satz von Dirichlet besagt, sondern auch gleichmäßig.


Beispiel 2: (Sägezahnfunktion)

Sei [math] g: \mathbb{R} \rightarrow \mathbb{R} \; 2 \pi [/math]-periodisch und auf [math] [0, 2 \pi) [/math] gegeben durch

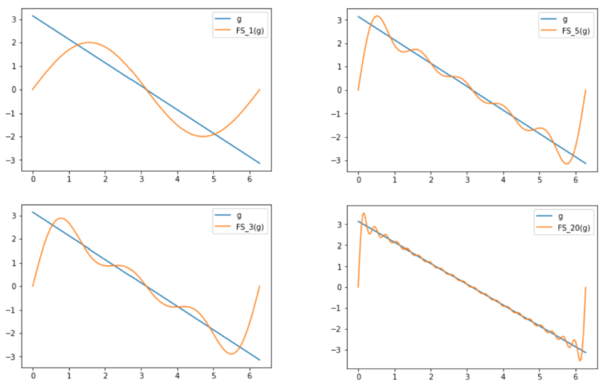
[math] g(x):= \pi - x [/math]

Nach dem Satz von Dirichlet konvergiert die Fourier-Reihe zu [math] g [/math] punktweise und nimmt dabei überall mit Außnahme der Sprungstellen den selben Wert wie [math] g [/math] an. Nun berechnen wir die Koeffizienten auch dieser Fourier-Reihe:


Zuerst stellen wir fest, dass für alle [math] n \in \mathbb{N}_0 [/math] gilt

[math] \begin{align} a_n &= \frac{1} {\pi} \int_0^{2\pi} g(x) cos(nx) \, dx \\ &= \frac{1} {\pi} \Bigl( \int_0^{\pi} g(x) cos(nx) \, dx + \int_{\pi}^{2\pi} g(x) cos(nx) \, dx \Bigl) \end{align} [/math]

Da aber gilt [math] g(\pi +x)cos(\pi + x) = - g(\pi - x)cos(\pi - x) [/math], folgt:

[math] \int_0^{\pi} g(x) cos(nx) \, dx = -\int_{\pi}^{2\pi} g(x) cos(nx) \, dx \; \Rightarrow \; a_n = 0 [/math]

Annäherungen von [math] g [/math] durch Partialsummen von [math] FS(g) [/math] auf dem Intervall [math] [0, 2 \pi ] [/math]


Weiter berechnen wir

[math] \begin{align} b_n &= \frac{1} {\pi} \int_0^{2\pi} g(x) sin(nx) \, dx \\ &= \frac{1} {\pi} \int_0^{2\pi} (\pi - x ) sin(nx) \, dx \\ &= - \frac{1} {\pi} \int_0^{2\pi} x sin(nx) \, dx + \frac{1} {\pi} \int_0^{2\pi} sin(nx) \, dx \\ &= - \frac{1} {\pi} \int_0^{2\pi} x sin(nx) \, dx \end{align} [/math].

Nun verwenden wir partielle Integration, um zu schließen

[math] \begin{align} b_n &= \frac{1} {\pi n} \Bigl( \Bigl[ xcos(nx) \Bigl]_{0}^{2 \pi} - \int_0^{2\pi} cos(nx) \, dx \Bigl) \\ &= \frac{1} {\pi n} \Bigl[ xcos(nx) \Bigl]_{0}^{2 \pi} = \frac{2 \pi} {\pi n} = \frac{2}{n} \end{align} [/math]


Somit besitzt die Fourier-Reihe zu [math] g [/math] folgende Darstellung:

[math] 2 \sum_{n = 1}^{\infty} \frac{sin(nx)}{n} [/math]


Wir stellen fest, dass die Reihe [math] \sum_{n = 1}^{\infty} b_n [/math] nicht konvergiert, da sie bis auf den Vorfaktor [math] 2 [/math] der divergenten harmonischen Reihe entspricht. Dies ist wenig überraschend, da die Fourier-Reihe zu [math] g [/math] andernfalls gleichmäßig konvergieren müsste, da sich der Beweis der gleichmäßigen Konvergenz der Reihe aus Beispiel 1 analog für [math] FS(g) [/math] führen ließe. Dass sie dies nicht tut, ist daran zu erkennen, dass [math] FS(g) [/math] nach dem Satz von Dirichlet an den Sprungstellen von [math] g [/math] nicht stetig sein kann, aber alle Summanden der Reihe stetige Funktionen sind, eine Eigenschaft die unter gleichmäßiger Konvergenz erhalten bliebe. Anschaulich äußert sich die fehlende gleichmäßige Konvergenz darin, dass die Partialsummen von [math] FS(g) [/math] an den Intervallgrenzen "überschwingen", wodurch die Reihe dort sehr viel langsamer konvergiert.

Zeichnen mit Fourierreihen

Man zeichnet einen 2-D Graph in die komplexe Ebene, wobei dieser Graph einer Funktion [math] f:[ 0, 1] \rightarrow \mathbb{C} [/math] ist und [math] f(t) = \sum_{k \in \mathbb{Z}} c_k e^{k2 \pi it} [/math] als Fourier-Reihe dargestellt wird. Dazu werden um die eigene Achse rotierende Zeiger benutzt, die der Reihe nach am Ende des Vorgängers verknüpft werden und am Punkt (0,0) starteen. Das Ende des letzten Zeigers zeichnet das gewünschte Bild. Die Zeiger haben unterschiedliche Frequenzen, entsprechend dem Faktor [math]k[/math] im Exponenten von [math] e^{k2 \pi it} [/math]. Außerdem bestimmt der Vorfaktor [math] c_k [/math] die Ausrichtung des Zeigers und den Radius des Kreises. Dieser Vorfaktor [math] c_k [/math] kann relativ leicht durch die folgende Formel bestimmt werden:

[math] \displaystyle c_k= \int_0^{1} f(t)e^{ - k2 \pi it} \, dx [/math]

So lassen sich beliebige Bilder zeichnen, die präziser dargestellt werden, je mehr Zeiger man verwendet.

Fouriertransformation

Anschauung

Die Fouriertransformation ist ein Teil der Fourieranalyse. Es geht dabei darum, aus aperiodischen Signale ein kontinuierliches Spektrum zu transformieren. Dies gelingt mittels einer Integraltransformation. Wir wollen eine zeitabhängige Funktion in eine frequenzabhängige transformieren. Diese Transformation stellt sich wie folgt dar:

[math] f(\omega ) = \int_{-\infty}^\infty F(t) e^{-i \omega t} dt [/math]

Wobei [math]F[/math] eine integrierbare Funktion und [math]f[/math] die (kontinuierliche) Fourier-Transformierte darstellt.


Inverse Fouriertransformation

Diese Transformation ist invertierbar. Dies nennt man dann die inverse Fouriertransformation. Diese Umkehrung stellt sich wie folgt dar:

[math]F(x) = \frac{1}{2\pi}\int_{-\infty}^{\infty} f(\omega)e^{i\omega t} d\omega[/math]

Beweis der Inversen

Nun wollen wir nachweisen, dass dies tatsächlich die Inverse der Fourier Transformation ist. Dafür setzen wir für [math]f(\omega)[/math] die obige Gleichung für die Transformation ein:

[math]\frac{1}{2\pi}\int_{-\infty}^{\infty} f(\omega)e^{i\omega t} d\omega \\ = \frac{1}{2\pi}\int_{\omega = -\infty}^{\infty} (\int_{\tau = -\infty}^{\infty}F(\tau)e^{-i\omega \tau}d\tau)e^{i\omega t} d\omega \\ =\frac{1}{2\pi}\int_{\tau = -\infty}^{\infty} F(\tau)(\int_{\omega = -\infty}^{\infty}e^{-i\omega (\tau -t)}d\omega) d\tau \\ = \int_{-\infty}^\infty F(\tau)\delta(\tau -t) d\tau \\ = f(t) [/math]

Beispielhafte Berechnung einer Transformierten

[math] f(x) = e^{-\mid x\mid }[/math]

Es gilt nach Euler-Moivre: [math] \rightarrow \ e^{-ixy} = cos(xy)-isin(xy)[/math]
f gerade [math] \rightarrow \ \int_{-\infty}^{\infty} f(x) \sin(xy)dx = 0[/math]

[math]F(y) = 2 \int_0^\infty e^{-x} \cos(yx)dx \underset{\text{part.Int.}}{=} 0+2\int_0^\infty e^{-x}\frac{\sin(yx)}{y} dx \\ \underset{\text{part.Int.}}{=} [ e^{-x}(-\frac{\cos(yx)}{y^2})]_0^\infty -2\int_0^\infty e^{-x}\frac{\cos(yx)}{y^2}dx \\ = \frac{2}{y^2} -\frac{F(y)}{y^2} [/math]

Umformung nach [math]F(y)[/math] [math] \rightarrow \ F(y)= \frac{2}{(1+y^2)}[/math]

Anwendungsbeispiele

Die Fouriertransformation findet in einigen Bereichen Anwendung.

  1. Kompressionsverfahren: Mithilfe der Fouriertransformation können MP3-Dateien in die Frequenzen zerlegt werden. Nun können solche, welche für den Menschen sowieso nicht wahrnehmbar sind aussortiert werden und die Datei somit verkleinert.
  2. Magnetresonanztherapie: Bei dieser Therapie werden bestimmte Atome durch Magnetwellen in Schwingung versetzt und ihre Resonanz gemessen. Mithilfe der Fouriertransformation werden die Frequenzanteile in horizontale und vertikale geteilt. Anschließend erhält man eine Kombination aus Phasen- und Frequenzkodierung. Diese können mithilfe der inversen Fouriertransformation in ein dreidimensionales Bild umgewandelt werden.
  3. Klangaufbereitung: Mithilfe der Fouriertransformation können störende hochfrequentische Klänge gefunden und eliminiert werden.

Quellen

Weiterführende Links

Abgerufen von „https://funfacts.mathi.uni-heidelberg.de/index.php?title=Fourieranalyse&oldid=4997“