Zauberwürfel
Symmetrische Gruppe
Die Symmetrische Gruppe [math]S_n[/math] ist die Gruppe, die aus allen Permutationen (Vertauschungen) einer Menge besteht. Man bezeichnet [math] n \in ℕ [/math] den Grad der Gruppe (Anzahl der Elemente).
Der Operator in der symmetrischen Gruppe ist die Komposition (Hintereinanderausführung) der Permutationen.
Das neutrale Element der Gruppe ist die Identitätsabbildung, welche bewirkt, dass keine Permutation stattfindet.
Die symmetrische Gruppe [math]S_n[/math] ist endlich und besitzt die Ordnung [math]n![/math].
Für Kardinalität [math]n\gt 2[/math] ist die [math]S_n[/math] nichtabelsch.
- [math] σ = \begin{pmatrix} LA & FF & DC & PTP & PEP \\ DC & LA & FF & PTP & PEP \end{pmatrix} [/math]
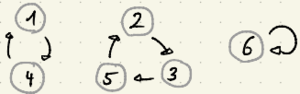
Zykelschreibweise
Die Vertauschungen werden häufig in sogenannten "Zykeln" geschrieben. Dabei werden die Positionen die durch die Vertauschungen geändert werden hintereinander in eine Klammer geschrieben. Dementsprechend ist die Zykelschreibweise nicht eindeutig. ?Die klassische Notation ist in der Klammer aufsteigend?.