Anwendungen der Knotentheorie

Knoten und Graphen

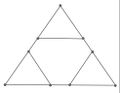
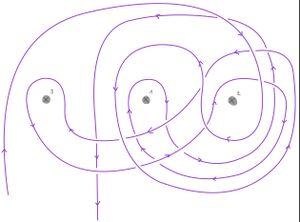
Jeder Knoten lässt sich auch als Graph darstellen. Hierfür betrachtet man den Außenbereich des Knoten, der durch die äußerste Linie abgetrennt wird und sein Inneres. Dann färbt man den Knoten schachbrettartig ein, indem man außen farbig beginnt und dann die einzelnen Gebiete gerade entgegengesetzt zu denjenigen auf der anderen Seite eines Strangs färbt. Dann verbindet man die Mittelpunkte, die so zu Ecken des Graphen werden, der weißen Gebiete, die damit zu Ecken des Graphen werden, so, dass die Verbindungslinie stets den Punkt schneidet, an dem sich benachbarte weiße Flächen treffen und erhält so die Kanten des Graphen. Schneidet die Kante des Graphen eine positive Kreuzung, d.h. eine Kreuzung, bei der der von links kommende Strang oben liegt, so wird die Kante durchgezogen. Handelt es sich um eine negative Kreuzung, bei der der von links kommende Strang unten liegt, so wird die Kante gestrichelt.

• 

  Beliebiger Knoten

• 

  Schachbrettartige Schraffierung und eingezeichnete Ecken des Graphen

• 

  Verbindung der Eckpunkte zu einem Graphen

• 

  Zugrundeliegender Graph

Umgekehrt können aus Graphen Knoten entstehen. Hierfür zeichnet man je in die Mitte der Kante ein Kreuz, das die Kante in einem Winkel von 45° schneidet. Die Enden nebeneinanderliegender Kreuze, d.h. solcher Kreuze, deren Kanten sich in einer Ecke treffen, werden verbunden. Anschließend verteilt man abwechselnd an den Kreuzen linke und rechte Kreuzungen. Auf diese Art sind einige berühmte keltische Muster entstanden.

• 

  Dreieckiger Graph

• 

  Graph mit Kreuzen

• 

  Verbundene Kreuze

• 

  Fertiger Kleeblattknoten

Krawatte binden

Entweder hat Mann es als Kind von seinem Vater gelernt, eine*n talentierte*n Partner*in oder ist und bleibt auf Schnellverschlüsse angewiesen, wenn Mann eine Krawatte tragen möchte. Die meisten dürften nicht sehr viele verschiedene Knoten kennen, dabei existieren 85 mögliche Knoten zum Binden einer Krawatte mit 8 Zügen, die allerdings nicht alle Balance, Symmetrie und Form berücksichtigen, wie der theoretische Physiker Thomas Fink und die Mathematikerin Yong Mao herausfanden . Aus praktischen Gründen werden also nicht alle davon realisiert, zum Einen sind unendlich lange Krawatten leider noch nicht erfunden, zum Anderen müsste Mann dann eventuell einen sehr schweren, unförmigen Krawattenknoten um den Hals tragen und bekäme davon bestimmt Rückenschmerzen. Dieser Gedanke lässt sich auch noch weiterführen. Wir wollen uns fragen, wie viele Möglichkeiten es gibt, eine Krawatte mit 13 Zügen zu binden, denn gerade schmale Krawatten werden häufiger umeinandergeschlungen und -gewickelt als breite .

Zunächst führen wir eine Sprache ein, um eine Krawatte und ihren Knoten allgemein beschreiben zu können. Wir führen ein, dass wir immer ein aktives schmales Ende der Krawatte haben und das andere, breite Ende festhalten, damit es nicht verrutscht. Weiterhin teilen wir den werten Krawattenbinder in drei Regionen ein, die durch seine Krawatte abgetrennt werden, einen linken, einen rechten und einen zentralen Teil und bezeichnen sie mit [math] L [/math], [math] C [/math] und [math]R[/math] (left, center, right). Wir schreiben [math]\odot[/math], wenn wir die den schmalen Teil der Krawatte "aus der Ebene hinaus" ziehen und [math]\otimes [/math], wenn wir den schmalen Teil der Krawatte "in die Ebene hinein" ziehen. Außerdem schreiben wir [math]U[/math] für eine Umwicklung, die nur dann erlaubt ist, wenn wir die Krawatte im letzten Zug "aus der Ebene heraus" gezogen haben. Mit großen Symbolen beschreiben wir also jeweils die Lage des breiten Endes der Krawatte, mit dem Index die Richtung, in der wir die Krawatte ziehen und [math]U[/math] beschreibt eine Umwicklung. Somit erhalten wir die folgenden möglichen Bewegungen, die wir mit der Krawatte durchführen können: [math]\{L_{\otimes}, L_{\odot}, C_{\otimes}, C_{\odot}, R_{\otimes}, R_{\odot}, U\}[/math] Um die Stabilität der Krawatte zu gewährleisten führen wir einige Regeln ein:

1. [math](L,C,R)[/math] darf sich nicht wiederholen, d.h. gleiche Symbole dürfen nicht aufeinander folgen.
2. [math]\otimes[/math] und [math]\odot[/math] dürfen sich nicht direkt wiederholen. [math]U[/math] ist unabhängig davon.
3. [math]U[/math] darf nur direkt auf eine Bewegung nach außen folgen.
4. Ein Knoten darf nur mit [math]C_{\otimes}, C_{\odot}, U[/math] enden.
5. Eine [math]k[/math]-fache Umschlingung ist erst erlaubt, wenn zuvor [math]2k[/math] andere Bewegungen ausgeführt wurden.

Wir können im Folgenden die Symbole [math]\otimes[/math] und [math]\odot[/math] direkt weglassen, da sich stets aus dem letzten rekonstruieren lässt, mit welcher Bewegung wir begonnen haben (die letzte Bewegung muss nach außen gehen und außen und innen müssen sich stets abwechseln). Weiterhin können wir die Krawatte entweder im ([math]T[/math]) oder gegen den Uhrzeigersinn ([math]W[/math]) umschlingen, denn [math] RUR [/math], [math] CUC [/math] und [math] LUL [/math] können nicht auftreten wegen unserer ersten Annahme. Die Position des aktiven (schmalen) Teils der Krawatte lässt sich dann beschreiben als [math]\#W-\#T (mod 3)[/math]. Elementare Überlegungen führen uns auf die Tatsache, dass wenn wir den Krawattenknoten mit [math]W[/math] begonnen haben gelten muss [math]\#W-\#T = 2 (mod 3)[/math] und wenn wir den Knoten mit [math]T[/math] begonnen haben gelten muss [math]\#T-\#W = 2 (mod 3)[/math] für eine k-fache Umwicklung einer 2k-langen Sequenz. Beweis?

Nun wollen wir eine Grammatik aufbauen, die beschreibt, wie wir die Krawatte binden können. Hierfür verwenden wir die Backus-Naur-Form .

Nun können wir für unseren Krawattenknoten Erzeugende Funktionen finden, die sich durch eine formale Potenzreihe [math] \begin{align}f(z) = \sum\limits_{n=0}^{\infty} a_nz^n \end{align}[/math] darstellen lassen. Mittels eines Computers und der zuvor definierten Grammatik lässt sich eine solche Erzeugenden Funktion finden. So wird ein einfacher Krawattenknoten beschrieben durch [math]\begin{align} \frac{2z^2(2z+1)}{1-6z^2} = 2z^3 + 4z^4 + 12z^5+24z^6+72z^7+144z^8+432z^9+864z^{10}+2592z^{11}+5184z^{12}+15552z^{13}+\mathcal{O}(z^{14}) \end{align} [/math]

Der Exponent beschreibt dabei stets die Windungszahl der Krawatte, also wie oft wir sie gewickelt haben und der Vorfaktor die jeweils möglichen Umschlingungen. Treffen wir nun die Annahme, dass der Träger ab 13 Umwicklungen wegen des wachsenden Gewichts des Knotens Rückenschmerzen bekommt, er sie so eng wickeln muss, dass er nicht mehr richtig Luft bekommt oder es einfach nicht mehr schön aussieht, können wir die Potenzreihe bei einem Exponenten von 13 abschneiden. Nun lässt sich für einen jeden Krawattenknoten eine solche Erzeugende Funktion finden, wobei wir durch zuvor gesetzte Parameter festlegen können, wie die Sequenz von Umschlingungen endet. Für 13 Windungen erhalten wir die folgenden Möglichkeiten:

Windungszahl	3	4	5	6	7	8	9	10	11	12	13	total
#right windings	1	1	3	5	11	21	43	85	171	341	683	1365
#left windings	0	2	2	6	10	22	42	86	170	342	682	1364
#center windings	1	1	3	5	11	21	43	85	171	341	683	1365
#left knots	0	2	4	8	24	48	144	288	864	1728	5184	8294
#right knots	1	1	4	8	24	48	144	288	864	1728	5184	8294
#center knots	1	1	4	8	24	48	144	288	864	1728	5184	8294
#single tuck knots	2	4	12	24	72	144	432	864	2592	4146	15552	84882
total #knots	2	4	20	40	192	384	1896	3792	19320	38640	202329	2666682

In dieser Zählung sind allerdings noch solche Krawattenknoten erlaubt, bei denen der die Krawatte falsch herum durchgezogen wurde und deshalb nicht ganz korrekterweise ein Krawattenknoten ist. Ziehen wir diesen Fehler ab, so erhalten wir eine maximale Anzahl möglichen Krawattenknoten mit 13 Bewegungen von 177146 Knoten.

Schuhe binden

Überkreuz- und Sägezahnschnürung

Was ist der effizienteste Weg, seine Schuhe zu binden? Ist es die klassische Überkreuzschnürung?

Wir gehen von einem idealen Schuh aus, welcher [math] 2n [/math] Ösen besitzt, [math]n\in \mathbb{N}[/math] auf jeder Seite, um die Schnürsenkel zu binden. Um den Schnürsenkel mathematisch beschreiben zu können, muss er geschlossen sein. In der realen Welt ließe sich dies durch das Binden einer Schleife realisieren. Unsere Schnürung besteht aus [math]2n[/math] Segmenten, wobei ein Segment jeweils die Verbindung zwischen zwei Ösen ist. Das heißt demzufolge auch, dass jede Öse nur einmal verwendet wird. Als weitere Anforderung verlangen wir, dass mindestens eines der beiden einlaufenden Schnürsenkelsegmente je Öse seinen Ursprung in der anderen Reihe der Ösen besitzt. Damit wollen wir sicherstellen, dass die zwei Seiten des Schuhs wirklich festgezogen werden.

Besitzt der Schuh auf jeder Seite gerade [math] n=1[/math] Löcher, so gibt es genau eine Möglichkeit, seinen Schuh zu binden. Betrachten wir also nun einen Schuh mit [math] n\geq2[/math] Löchern auf jeder Seite. Die Anzahl der möglichen Schnürungen bei [math] n[/math] Löchern ergibt sich nach einer komplizierten Rechnung zu

[math]\#(n)= \frac{(n!)^2}{2} \sum\limits_{k=0}^{m}\frac{1}{n-k}\binom{n-k}{k}^2 [/math]

mit [math] m=n/2[/math] für gerade [math]n[/math] und [math]m=(n-1)/2[/math] für ungerade [math]n[/math].

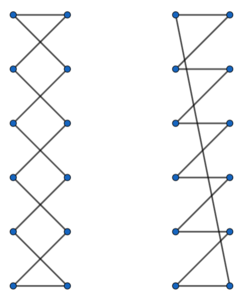
Die Länge einer Schnürung ist die Summe aus allen einzelnen Teilsegmenten. Unter der Verwendung von Symmetrien und Vereinfachungen ergibt sich folgendes Muster für die kürzeste Schnürung unter unseren Vorraussetzungen, wobei hier allerdings noch zwischen [math]n[/math] gerade oder ungerade unterschieden werden muss.

Unter unseren Voraussetzungen kürzeste Schnürung, links für [math] n[/math] gerade, rechts zwei Beispiele für [math] n[/math] ungerade

Diese Schnürung ist allerdings nicht die stärkste. Der Schnürsenkel funktioniert wie ein Flaschenzug, wenn er die zwei Reihen zusammenzieht. Allerdings hängt die Stärke der Schnürung vom Verhältnis der Abstände zwischen den einzelnen Ösen und den beiden Reihen ab. Es lässt sich ein kritisches Verhältnis [math]x_n[/math] finden, sodass für [math]x\leq x_n[/math]die Überkreuzbindung die stärkste Verbindung ist und für [math] x\geq x_n [/math]die Sägezahnbindung die stärkste Verbindung ist (siehe Bild rechts oben). Für reale Schuhe hingegen ist dieses Verhältnis meistens in der Nähe von [math] x_n[/math], sodass die Art der Bindung keine entscheidende Rolle spielt.

Zwei Nägel und ein Bild

Lösung des Zweinagelproblems

Meist werden Bilder ganz simpel und ohne mathematische Rafinesse an der Wand befestigt wie in Abb. ? gezeigt. Möchte der geschickte Mathematiker jedoch eine Weise finden, das Bild nur durch die Entfernung eines Nagels abhängen zu können (etwa um möglichst energiesparend an den dahinterliegenden Tresor zu gelangen), so braucht es hierfür eine geschicktere Konstruktion.

Eine mächtige Methode, einen geeigneten Knoten zu finden, funktioniert auf die folgende ARt und Weise: Man definiert für die Notation zunächst die Symbole [math]x_1,{x_1}^{-1},...,x_n, {x_n}^{-1}[/math], während hierbei jeweils [math]x_i[/math] die Umschlingung des [math]i[/math]-ten Nagels im Urzeigersinn und [math]{x_i}^{-1}[/math] jene gegen den Uhrzeigersinn beschreibt. Wendet man diese Notation auf das oben beschriebene Problem mit zwei Nägeln an, so kann man sich leicht davon überzeugen, dass

[math]S_2:=x_1x_2{x_1}^{-1}{x_2}^{-1}[/math]

eine Lösung ist, die die Voraussetzungen erfüllt. Denn sobald man nun einen Nagel hinauszieht, werden die darauf bezogenen Umschlingungen obsolet und es bleibt eine Umschlingung um den anderen Nagel im und eine gegen den Uhrzeigersinn übrig, wodurch das Bild auch diese scheinbare Aufhängung verliert und hinabfällt. Für die späteren Überlegungen lohnt es sich, dies als Kommutator [math][x1,x2]=x_1x_2{x_1}^{-1}{x_2}^{-1}[/math] einzuführen.

n-Nägel-Problem

Eine Lösung des Dreinagelproblems

Nun lässt sich diese Erkenntnis auch auf das Problem erweitern, ein Bild mit n Nägeln aufhängen zu wollen, welches erneut durch das Ziehen eines beliebigen Nagels abgehängt werden kann. Für das 3-Nägel-Problem wäre etwa eine Lösung, die bekannte 2-Nägel-Lösung [math]S_2[/math] zu nutzen und durch

[math][S_2,x_3]=S_2x_3{S_2}^{-1}{x_3}^{-1}=x_1x_2{x_1}^{-1}{x_2}^{-1}x_3x_2x_1{x_2}^{-1}{x_1}^{-1}{x_3}^{-1}[/math]

zu variieren. (Dies löst offensichtlich unser Problem, da bei Ziehung des ersten oder zweiten Nagels sowohl [math]S_2[/math] als auch dessen Inverses hinfällig wird und auch bei Ziehung des dritten Nagels nur noch eine Folge von Umschlingungen und ihr Inverses übrigbleiben, also das Bild ebenfalls hinabfällt.)

Analog ergibt sich für 4 Nägel erneut induktiv die folgende Lösung:

[math][S_3,x_4]=S_3x_4{S_3}^{-1}{x_4}^{-1}=...=x_1x_2{x_1}^{-1}{x_2}^{-1}x_3x_2x_1{x_2}^{-1}{x_1}^{-1}{x_3}^{-1}x_4x_3x_1x_2{x_1}^{-1}{x_2}^{-1}{x_3}^{-1}x_2x_1{x_2}^{-1}{x_1}^{-1}[/math]

Der bedeutende Nachteil dieser Methode ist ihre Ineffizienz: Man benötigt [math]2^n+2^{n-1}-2[/math] Umschlingungen. Der Beweis durch vollständige Induktion ist hier ausgeführt:
IA: Der behandelte Fall des 2-Nägel-Problems besitzt [math]2^2+2^1-2=4[/math] Umschlingungen.
IV: Die Aussage gelte für [math]n\in \lbrace2, i-1\rbrace[/math]
IS: Bezeichne [math]\# (S_i)[/math] die Anzahl der Umschlingungen bei der Lösung des i-Nägel-Problems. Wegen [math]S_i=[S_{i-1},x_i][/math] gilt dann mit der IV: [math]\#(S_i)=2\cdot\#(S_{i-1})+2=2\cdot(2^{i-1}+2^{i-2}-2)+2=2^i+2^{i-1}-2[/math]

Trivia

Wenn Ihnen dieser Artikel gefallen hat, könnte Ihnen auch das Museumswächterproblem gefallen. ^^

Quellen

http://export.arxiv.org/pdf/1401.8242 zum Krawatten binden

https://arxiv.org/pdf/1203.3602.pdf zum Nägelproblem

Autoren

Daniela Müller-Trefzer, Hjalmar Brunßen, Lasse Bassermann, Joris Hoffmann