Museumswächterproblem

Aus FunFacts Wiki
Zur Navigation springen Zur Suche springen

Das Museum ist wegen Corona geschlossen, deswegen werden keine Wächter benötigt:-(

Museum-Ritter

Zuerst betrachten betrachten wir das Museum-Ritter, welches zum gleichnamigen Schokoladenhersteller gehört. Natürlich ist der Grundriss in unserer idealisierten Mathewelt perfekt quadratisch. Der Museumsdirektor möchte nun Museumswächter einstellen und fragt sich, wie viele Leute er anstellen muss, wenn ein Wächter sich zwar nicht frei im Raum bewegen, aber sich um seine Achse drehen darf. Diese Frage ist trivial, es reicht ein Wächter irgendwo im Raum zu positionieren, wie relativ direkt aus der Definition der Konvexität folgt. Wie sieht es aber aus, wenn das Museum einen etwas komplizierteren Grundriss besitzt?

Satz

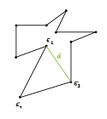
Nun betrachten wir ein Museum mit einem beliebigen Grundriss, welcher allerdings komplexer ist als der Grundriss des Museum-Ritter. Einzige Voraussetzung ist, dass sich alle Wände durch eine Gerade beschreiben lassen. Nun möchte unser Museumsdirektor wieder Wächter einstellen und fragt sich, wie viele er braucht, damit diese das komplette Museum im Blick haben. Auch hier gilt wieder, dass sich die Wächter nicht hin und her bewegen, sondern auf ihren Plätzen bleiben und sich nur um ihre Achse drehen können. Dann benötigt man folgende Anzahl an Wächtern:

Für jedes Museum mit [math]n[/math] Wänden reichen [math]\lfloor \frac{n}{3} \rfloor[/math] Wächter aus.

Beweis nach Steve Fisk

Um diesen Satz zu beweisen, müssen wir zuerst das Museum mathematisch beschreiben können. Dazu führen wir zwei Definitionen ein:

Definition: Polygon

Ein Polygon ist ein Tupel [math]P=: \left(P_1,P_2,\dots,P_n \right)[/math], von n verschiedenen Punkten [math]P_i,\ 1\leq i\leq n,\ n\in\mathbb{N}[/math]. Dabei heißen die n Punkte Eckpunkte des Polygons (man spricht auch von einem n-Eck) und die Strecken [math]\overline{P_iP_{i+1}}[/math] für [math] (1\leq i\leq n-1)[/math] und [math]\overline{P_1P_n}[/math] zwischen den Eckpunkten werden als Kanten oder Seiten bezeichnet. Die Verbindungsstrecken zweier Punkte die keinen Kanten sind werden als Diagonalen bezeichnet.
In unserem Fall betrachten wir nur planare Polygone, das heißt n-Ecken, welche in der Ebene liegen. Zusätzlich kann es sein, dass sich die Kanten nicht nur in den Eckpunkten schneiden, in diesem Fall spricht man von einem überschlagenen Polygon.

  • ein überschlagenes Polygon

  • ein konkaves Polygon

  • ein konvexes Polgon

Definition: Triangulation

Als Triangulation eines Polygons bezeichnen wir hier einen planaren Graph, welcher entsteht, wenn man die Innenfläche des Polygons durch Diagonalen, welche sich nicht schneiden, mit Dreiecken ausfüllt.

Für konvexe Polynome ist klar, dass eine Triangulation immer möglich ist

Satz: Für alle ebenen Polygone P existiert eine Triangulation

Beweis: Wir zeigen nun die Aussage für nichtkonvexe Polygone. Sei n die Zahl der Ecken.

IA: für n=3 ist P ein Dreieck also schon trianguliert.

IV: Der Satz gilt für alle Polygone mit weniger als n Ecken

IS: [math]n-1\rightarrow n[/math] Wir suchen eine Diagonale, die P in zwei Polygone [math]P_1[/math] und [math]P_2[/math] teilt. Dazu nehmen wir eine Ecke [math]E_1[/math] mit Innenwinkel kleiner als 180° (existiert immer) und verbinden die beiden zu [math]E_1[/math] benachbarten Ecken [math]E_2[/math] und [math]E_3[/math]. Nun sind 2 Fälle möglich:

Fall 1: [math]\overline{E_2E_3}[/math] ist vollständig in P enthalten. Dann ist mit dieser Diagonal das Polygon in zwei Polygone zerteilt mit jeweils weniger als n Ecken. Nach IV sind diese dann natürlich triangulierbar. Damit folgt die Behauptung auch für das gesamte Polygon.

Fall 2: [math]\overline{E_2E_3}[/math] ist nicht vollständig in P enthalten. Dann liegt also mindestens eine Ecke des Polygons innerhalb des Dreiecks [math]E_1E_2E_3[/math] liegt und kann durch eine Diagonale mit [math]E_1[/math] verbunden werden. Somit lässt sich das Polygon in 2 Polygone mit je weniger als n Ecken teilen, womit nach IV ebenfalls die Behauptung erfüllt ist.

Bemerkung: Im 3-dimensionalen ist eine Triangulation durch Tetraeder jedoch im Allgemeinen nicht möglich (vgl. Schönhardt-Polyeder).

Das Polygon hat 17 Ecken, davon vier rote, 7 blaue und 6 gelbe. Wenn man nun einen Wächter in die roten Ecken stellt. so reichen vier Wächter aus. Dies entspricht unserer Erwartung, dass wir höchstens [math] \lfloor \frac{17}{3}\rfloor = 5 [/math] Wächter benötigen.

  • Fall 1

  • Fall 2

Definition: Färbung

Sei E die Menge der Ecken eines Polygons und F die abzählbare Menge der Farben (oder Eigenschaften). Eine Färbung [math]f[/math] ordnet jeder Ecke eine Farbe zu, es handelt sich also um eine Abbildung [math]f: E\rightarrow F[/math]

Wir nennen eine Färbung eine 3-Färbung, falls:

(i) [math]\# F=3[/math]

(ii) je 2 benachbarte Ecken stets verschiedene Farben haben

Beweis:

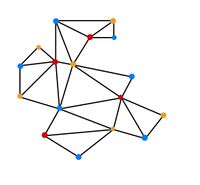
Für ein Museum mit [math]n=3[/math] Ecken ist die Anzahl der Wächter klar. Für ein Museum mit [math]n\gt 3[/math] Wänden beschreiben wir den Grundriss als Polygon. Wir verbinden alle Ecken mit [math]n-3[/math] sich nicht kreuzenden Diagonalen. Um nun die Anzahl der benötigten Wächter zu bestimmen, färben wir alle Ecken der Dreiecke in drei verschiedenen Farben ein, wir nehmen o.B.d.A die Farben rot, blau und orange. Dabei ist darauf zu achten, dass aneinanderliegende Ecken in benachbarten Dreiecken die selbe Farbe erhalten. Da unser Museum insgesamt [math]n[/math] Ecken besitzt, welche mit drei Farben eingefärbt wurden, gibt es höchstens [math]\lfloor \frac{n}{3} \rfloor[/math] Ecken einer Farbe. Wenn wir nun die Wächter in die roten (oder blauen oder orangenen) platzieren, reichen [math]\lfloor \frac{n}{3} \rfloor[/math] Wächter aus. Diese Wächter können auch auf jeden Fall ihr zugewiesenes Dreieck überblicken, da es konvex ist.

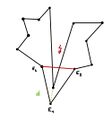
Beispielrechnung am Guggenheim-Museum Bilbao

Triangulation des Grundrisses des Guggenheim-Museum Bilbao
Guggenheim-Museum in Bilbao

Quellen

Abgerufen von „https://funfacts.mathi.uni-heidelberg.de/index.php?title=Museumswächterproblem&oldid=1180“