Zufallsmatrizen - Bohemians und die geheimnisvolle Ordnung im Chaos

• 

"Zufallsmatrix" - eine Matrix mit zufälligen Einträgen - klingt zuerst einmal vielleicht nach etwas Willkürlichem. Wie daraus solche faszinierenden Bilder entstehen, was man sonst noch alles damit anstellen kann und welche Möglichkeiten sich für die Forschung in der Physik und anderen Wissenschaften ergeben, soll in diesem Artikel gezeigt werden.

Den Anstoß zur Forschung im Bereich der Zufallsmatrizen gab der Physiker Eugene Wigner, der bei der Analyse von schweren Atomkernen darauf stieß, dass das Resonanzspektrum schwerer Kerne bei hohen Energien durch die Eigenwerte von Zufallsmatrizen beschrieben werden kann. Seit dieser Entdeckung Wigners werden zufällige Matrizen in verschiedenen Bereichen der Quantenphysik verwendet, z.B. als spektrale Signatur von Quantenchaos, zur Beschreibung mesoskopischer Systeme mit Unordnung oder in der Quantenchromodynamik. Das Vorkommen der Zufallsmatrizen in verschiedenen Bereichen zeigt, dass diese eine gewisse Universalität besitzen. Der stochastische Mechanismus, der zu solchen Verteilungen führt, ist bislang jedoch nicht allgemein verstanden. In den Spezialfällen, für die Beweise existieren, liegen explizite Formeln für die Verteilungen vor, die mit allerlei Tricks analysiert werden können. Die Beweise brechen allerdings schon bei kleinen Abwandlungen der Modelle in sich zusammen.

Zufallsmatrizen

Definition

Eine Zufallsmatrix ist eine Matrix, deren Einträge teils oder ganz zufällig sind.

Universelle Eigenschaften

Kurven der Wigner-Verteilungen

Es gibt offensichtlich sehr viele Methoden, solche Matrizen auszuwählen, dabei kann die Wahrscheinlichkeitsverteilung der Einträge, die Menge, aus der man die Einträge nimmt oder die Form der Symmetrie der Matrizen sehr stark variieren. Wir betrachten nun Matrizen, die symmetrisch bzgl. der Diagonale sind und deren Einträge unabhängig voneinander gemäß der Normalverteilung ausgewählt werden.

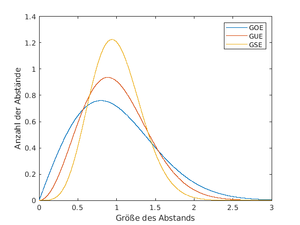
Lässt man die Größe dieser Matrizen gegen Unendlich gehen, ergeben die Abstände zwischen aufeinanderfolgenden Eigenwerten dieser Matrizen eine bestimmte Kurve (siehe Bild). Die Klasse der Zufallsmatrizen, deren Eigenwertabstände dieser Kurve folgen, nennt man gaußsches orthogonales Ensemble (GOE).

Analog ergeben Eigenwertabstände von hermiteschen Zufallsmatrizen eine andere Kurve, diese Klasse nennt man gaußsches unitäres Ensemble (GUE).

Beispiel Hermitischer Matrix:

• Eine hermitesche Matrix ist eine symmetrische Matrix mit komplexen Einträgen, bei der Spiegelung wird das Vorzeichen des Imaginärteils gedreht (komplex konjugiert): [math]\,\begin{pmatrix} 1 & 2 & 3+i \\ 2 & 5 & 6-2i \\ 3-i & 6+2i & 7 \end{pmatrix}\,[/math]Ihre Eigenwerte sind alle reell.

Diese Kurven gehören zu den sogenannten Wigner-Verteilungen, benannt nach dem oben genannten Physiker Eugene Wigner.

Seitdem wurden viele weitere Familien von Zufallsmatrizen untersucht und dabei andere Ensembles entdeckt, deren Eigenwertabstände anderen Kurven folgen. Man fand dabei heraus, dass diese Eigenwertabstände nicht von der Wahrscheinlichkeitsverteilung der Einträge abhängig sind, sondern nur von den Symmetrien der entsprechenden Matrizen. Der Grund dafür ist die extreme Größe der Matrizen. Dadurch heben sich nämlich die komplizierten Effekte der Eigenwertberechnung im Mittel auf, und die Funktion strebt gegen einen Durchschnittswert. Allerdings lassen sich diese universellen Eigenschaften schwer beweisen und bis heute gibt es noch viele offene Probleme in diesem Teilgebiet.

Nicht universelle Eigenschaften

Eigenwertdichte von einer symmetrischen 1500x1500 Matrix mit Einträgen aus einer Normalverteilung

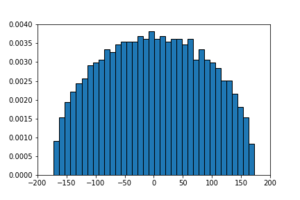
Eine Eigenschaft einer Zufallsmatrix ist nicht universell, wenn sie von der Wahrscheinlichkeitsverteilung der Einträge abhängt, ein Beispiel dafür ist die Dichte der Eigenwerte. Allerdings gibt es auch hier interessante Gesetzmäßigkeiten, wie zum Beispiel die sogenannten Wigner-Halbkreise. Dabei handelt es sich wieder um symmetrische Zufallsmatrizen, deren Einträge gemäß der Normalverteilung ausgewählt werden. Diesmal trägt man nicht die Eigenwertabstände in einem Histogramm auf, sondern die Häufigkeit von einzelnen Eigenwerten. Dies ergibt einen Halbkreis mit Mittelpunkt im Ursprung. Je größer die Zufallsmatrizen sind, desto mehr nähert sich das Histogramm einem Halbkreis an.

Anwendungsgebiete

Zufallsmatrizen können in den unterschiedlichsten, teils überraschenden Themengebieten genutzt werden, um (Natur-)Phänomene zu beschreiben oder Daten zu modellieren.

So etwa bei:

• Verknüpfung von Neuronen im Gehirn, künstlicher Intelligenz und maschinellem Lernen
• Datenkompression/Signalübertragung, Mobilfunk
• Finanzwirtschaft (Fluktuation von Börsenkursen)
• der Statistik ankommender U-Bahnen in New York, Abstände parkender Autos und von Bäumen im Urwald

Warum genau es so gut funktioniert, diese doch sehr unterschiedlichen Dinge treffend durch Zufallsmatrizen zu beschreiben, ist überwiegend unbekannt.

Nicht nur in praktischen Anwendungsgebieten werden Zufallsmatrizen benutzt: Auch bei theoretischen Problemen in der Mathematik, wie dem Beweis der Riemannschen Vermutung, sind Zufallsmatrizen ein vielversprechender Ansatz, zu einer Lösung zu gelangen. Beispielsweise über eine (hypothetische) Matrix, von den Wissenschaftlern Riemannium getauft, deren Eigenwerte den Nullstellen der Riemannschen Zeta-Funktion entsprechen.

Eine Klasse von Zufallsmatrizen, die besonders viel mit der Dichte von Eigenwerten zu tun hat, ist die sogenannte Klasse der Bohemian Matrices. Auch Fraktale wie Julia- und Mandelbrotmengen tauchen im Zusammenhang mit Zufallsmatrizen auf (vgl. Bohemians mit Einträgen aus diskreter Menge, sowie die externe Galerie [1]).

Im Folgenden werden beispielhaft zwei sehr unterschiedliche Anwendungsgebiete genauer ausgeführt.

Bildverarbeitung

Zufallsmatrizen sind jedem von uns sicherlich schon einmal in einem ihrer praktischen Anwendungsgebiete begegnet: Der digitalen Bildverarbeitung.

Bei der Aufnahme von Fotos begegnet man oft dem sogenannten Bildrauschen, bei dem ein Bild störende Pixel aufweist, die in Farbe und Helligkeit deutlich von eigentlichen Bild abweichen. Dies tritt vor allem bei einer schlechten Belichtungssituation, wie während der Dämmerung oder nachts, auf.

Es existieren verschiedene Arten von derartigen Bildstörungen, u. a. das Gaußsche Rauschen, dessen Wahrscheinlichkeitsverteilung mithilfe der Normalverteilung als Formel beschrieben werden kann: [math]\frac{1}{\sqrt{2 \cdot \pi \cdot \mu}} \cdot e^{-\frac{x^2}{2 \cdot \mu}}[/math].

Unter der Annahme, dass jede zu diesen Pixeln assoziierte Matrix zufällig ist und damit ihre Eigenwertdichte berechenbar ist, kann man, indem man herausfindet, in welchem Maße sich der Eigenwert des Originalbilds zu dem des verrauschten Bildes verändert, das störende Gaußsche Rauschen eliminieren. Dabei werden die wichtigen Informationen des Originalbildes beibehalten.

Quantenmechanik

Die Untersuchung schwerer Atomkerne bzw. das Messen ihrer unterschiedlichen Energieniveaus ist nicht ganz einfach, wie man vermuten kann, wenn man die Schrödingergleichung [math]\mathrm i \hbar \frac{\partial \psi}{\partial t} = - \frac{\hbar^2}{2m} \nabla^2 \psi + V \psi[/math] betrachtet ([math]\hbar[/math] ist die reduzierte Plancksche Konstante). In diesem Zusammenhang erwähnenswert ist der sogenannte Hamilton-Operator, welcher angewendet auf den Zustand eines quantenmechanischen Systems dessen zeitliche Entwicklung beschreibt.

Wenn man nun [math]H \psi := \mathrm i \hbar \frac{\partial \psi}{\partial t}[/math] sowie [math]E \psi := - \frac{\hbar^2}{2m} \nabla^2 \psi + V \psi[/math] definiert, kann die erste Gleichung vereinfacht als [math]H \psi = E \psi[/math] geschrieben werden. [math]H[/math] ist der Hamilton-Operator, [math]\psi[/math] ein Eigenvektor und [math]E[/math] der korrespondierende Eigenwert, hinter welchem sich die verschiedenen Energieniveaus verbergen. Auch die allgemeinste Form der Schrödingergleichung [math]\mathrm{i}\hbar\frac{\partial}{\partial t} |\,\psi (t) \rangle = \hat{H} |\,\psi (t) \rangle[/math] (wobei [math]\hat{H}[/math] der Hamilton-Operator und [math]|\,\psi (t) \rangle[/math] der Zustandsvektor sind) macht den Zusammenhang zu Eigenwerten sichtbarer.

Nach Eugene Wigner kann nun, statt mit dem komplizierten Hamilton-Operator (welcher auf einem unendlich-dimensionalen Vektorraum definiert ist) zu arbeiten, die Verteilung der Eigenwerte einer Familie von Zufallsmatrizen betrachtet werden, um auf die Verteilung der Energieniveaus zu schließen. Dies geschieht, indem man nach Werten sucht, gegen welche diese Verteilung läuft (asymptotisches Verhalten), wenn die Größe dieser Matrizen gegen unendlich geht.

Bohemian Matrices

Bohemian Matrices sind eine bestimmte Form von Zufallsmatrizen. Der Name Bohemian steht dabei für bounded height integer matrix eigenvalues, woraus aus der Abkürzung BHIME dann Bohemian wurde. Ihre Untersuchung ist ein recht neues und noch relativ unerforschtes Gebiet und wird bislang im Rahmen der angewandten Mathematik betrachtet. Durchleuchtet werden dabei bspw. die Verteilung der Eigenwerte, ihre Symmetrien sowie Zahlenfolgen, die sich aus ihren Eigenschaften ergeben. Diese weisen überraschend oft Querverbindungen mit anderen Bereichen der Mathematik auf.

Bohemian Matrices sind Zufallsmatrizen, deren Einträge auf eine Menge ganzer Zahlen aus einem endlichen Intervall beschränkt sind, wie z. B. [math]\{-1, 0, 1\}[/math]. Die ausgewählten Zahlen sind dabei unabhängig von der Dimension der Matrix. Das Feld der Bohemian Matrices umfasst mittlerweile auch Matrizen mit Einträgen aus kontinuierlichen bzw. nicht-endlichen Mengen, obwohl diese nach dieser Namensgebung streng genommen nicht mit inbegriffen wären. Zusätzlich kann eine bestimmte Struktur der Matrix vorgegeben werden (z. B. Diagonalmatrix, Dreiecksmatrix etc.).

Wie macht man daraus Bilder?

Um die Eigenwerte der Zufallsmatrizen zu visualisieren, wird zunächst ein Satz von Matrizen nach dem gewünschten Muster generiert. Die Anzahl liegt dabei meist zwischen [math] 10^6[/math] und [math]10^7[/math] und die Größe etwa zwischen [math]3 \times 3 [/math] und [math]20 \times 20 [/math]. Bei nur schwach zu sehenden Mustern müssen teilweise auch deutlich mehr Matrizen einberechnet werden, um ein besseres Bild zu erhalten.

Von diesen Matrizen werden dann die Eigenwerte und deren Dichte berechnet, das heißt je häufiger ein Eigenwert in den Matrizen vorkommt, desto stärker fällt dieser ins Gewicht.

Real- und Imaginärteil dieser Dichte werden dann in der komplexen Zahlenebene aufgetragen, wobei die Farbe nach einem vorher ausgewählten Farbschema anhand der Dichte festgelegt wird.

Der Code zum Berechnen der Bilder ist frei verfügbar für Python: https://github.com/BohemianMatrices/bohemian-python und Matlab: https://github.com/BohemianMatrices/BHIME-Project. Die Bilder in diesem Artikel wurden in Matlab generiert.

Galerie

Je nachdem, wie man die Einträge und die Struktur einer Zufallsmatrix auswählt, kommen bei der Betrachtung der Eigenwertdichte unterschiedliche Muster und Formen zustande. In dieser Galerie sollen einige davon mit den zugehörigen Bildern vorgestellt werden. Es handelt sich bei allen Bildern um unsere Eigenkreationen (no pun intended).

Zufällige Matrix mit Einträgen aus diskreter Menge

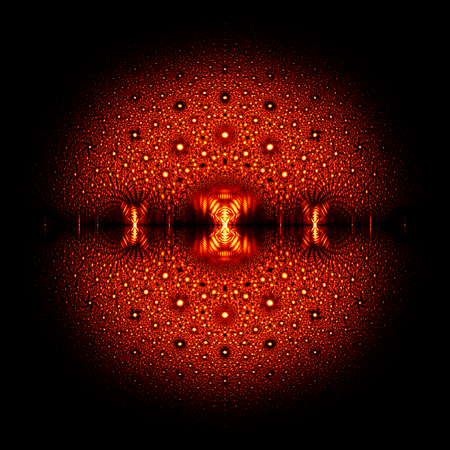
Die wohl einfachste Art von Zufallsmatrizen sind [math]n\times n[/math] Matrizen, bei denen jeder Eintrag zufällig aus einer endlichen Menge von vorher festgelegten Werten ausgewählt wird. Dabei entstehen Muster mit annähernd fraktal aussehenden Strukturen entlang der reellen Achse.

• 

  Eigenwertdichte von 10 Millionen [math]6 \times 6 \:[/math] Matrizen mit Einträgen aus der Menge [math] \{-1, -\frac{1}{1000}, 0, \frac{1}{1000}, 1\} [/math]

• 

  Zoom in die Mitte des linken Bildes

• 

  "Eigenkäfer" - Eigenwertdichte von 10 Millionen [math]6 \times 6\:[/math]Matrizen mit Einträgen aus der Menge [math] \{-1, -\frac{1}{100}, 0, \frac{1}{1000}, 12\} [/math]

Betaverteilung

Bei diesen Matrizen werden alle Einträge zufällig aus einer Betaverteilung mit vorher festgelegten Parametern generiert. Zusätzlich wird eine Amplitude und Verschiebung hinzugefügt, sodass die Einträge von der Form [math]A \cdot x+b[/math] sind, wobei [math]x[/math] der Wert aus der Betaverteilung ist. Dadurch entstehen je nach Wahl der Parameter Linienmuster, auf denen sich die Eigenwerte häufen.

• 

  Eigenwertdichte von 15 Millionen [math]6\times 6[/math] Matrizen mit Werten aus einer Betaverteilung mit den Parametern [math] \alpha = 0{,}001, \: \beta = 0{,}001 [/math] (die Eigenwerte wurden an der imaginären Achse gespiegelt)

• 

  Eigenwertdichte von 5 Millionen [math]3\times 3[/math] Matrizen mit Werten aus einer Betaverteilung mit den Parametern [math] \alpha = 0{,}01, \: \beta = 0{,}01, \: A=5, \: b=-0{,}5[/math] (die Eigenwerte wurden an der imaginären Achse gespiegelt)

• 

  Eigenwertdichte von 30 Millionen [math]6\times 6[/math] Matrizen mit Werten aus einer Betaverteilung mit den Parametern [math] \alpha = 0{,}001, \: \beta = 0{,}01, \: A=5, \: b=-2 [/math] (die Eigenwerte wurden an der imaginären Achse gespiegelt)

Obere Hessenbergmatrix / Tridiagonalmatrix

Eine obere Hessenbergmatrix ist ähnlich wie eine obere Dreiecksmatrix, nur dass diese auch Einträge auf der ersten Nebendiagonalen unter der Hauptdiagonalen besitzt.

Beispielsweise ist [math]\,\begin{pmatrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 0 & 9 & 10 & 11 \\ 0 & 0 & 12 & 13 \end{pmatrix}\,[/math] eine obere Hessenbergmatrix. Analog ist [math]\,\begin{pmatrix} 1 & 2 & 0 & 0 \\ 3 & 4 & 5 & 0 \\ 6 & 7 & 8 & 9 \\ 10 & 11 & 12 & 13 \end{pmatrix}\,[/math] eine untere Hessenbergmatrix.

Eine Tridiagonalmatrix ist sowohl eine obere als auch eine untere Hessenbergmatrix und hat somit nur Einträge auf der Hauptdiagonalen und den beiden angrenzenden Nebendiagonalen, wie z. B. [math]\,\begin{pmatrix} 1 & 2 & 0 & 0 \\ 3 & 4 & 5 & 0 \\ 0 & 6 & 7 & 8 \\ 0 & 0 & 9 & 10 \end{pmatrix}\,[/math].

• 

  Eigenwertdichte von 20 Millionen [math]12 \times 12[/math] oberer Hessenbergmatrizen mit Toeplitz-Struktur und Einträgen aus der Menge [math]\{-1, 0, 1\}[/math]

• 

  Eigenwertdichte von 10 Millionen [math]10 \times 10[/math] Tridiagonalmatrizen mit Einträgen aus der Menge [math]\{-π, π\}[/math]

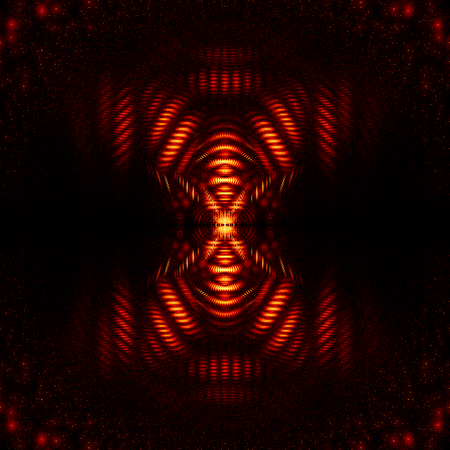
Feste Matrix mit kontinuierlicher Verteilung in bestimmten Werten (Eigenfish)

Hier wurden Matrizen von der Form [math]\,\begin{pmatrix} 0 & 0 & 0 & A \\ -1 & -1 & 0 & 0 \\ B & 0 & 0 & 0 \\ -1 & 1 & 1 & -1 \end{pmatrix}\,[/math] verwendet. Die Einträge A und B wurden dabei zufällig aus einem kontinuierlichen Intervall ausgewählt.

Kleine Änderungen an den Einträgen der Matrix können dabei vollkommen unterschiedliche Formen hervorbringen. Für die Bilder wurde die obige Matrix teilweise leicht verändert und es wurden unterschiedliche Intervallgrenzen ausgewählt.

• 

  Eigenwertdichte von 3 Millionen Matrizen

• 

  Eigenwertdichte von 3 Millionen Matrizen

• 

  Animation von Matrizen mit [math]A,B \in [-\pi(1+i),\pi(1+i)][/math], wobei der Imaginärteil der unteren Grenze im Laufe der Animation bis auf [math]20i[/math] erhöht wurde.