Zauberwürfel
Der Zauberwürfel ist ein Drehpuzzle in Würfelform. Durch ihn kann man sich die Symmetrische Gruppe anschaulich vorstellen und mit ihrer Hilfe Aussagen über die Lösbarkeit des Würfels treffen.
Symmetrische Gruppe
Die Symmetrische Gruppe [math]S_n[/math] ist die Gruppe, die aus allen Permutationen (Vertauschungen) einer [math] n [/math]-elementigen Menge besteht. Man bezeichnet [math] n \in ℕ [/math] den Grad der Gruppe (Anzahl der Elemente).
Die Gruppenoperation in der symmetrischen Gruppe ist die Komposition (Hintereinanderausführung) der Permutationen.
Das neutrale Element der Gruppe ist die Identitätsabbildung, welche bewirkt, dass keine Permutation stattfindet.
Die symmetrische Gruppe [math]S_n[/math] ist endlich und besitzt die Ordnung [math]n![/math].
Für Grad [math]n\gt 2[/math] ist die [math]S_n[/math] nichtabelsch. [1]
Zur Veranschaulichung folgt ein Beispiel anhand eines Bücherregals:
Zunächst führen wir die Anfangsaufstellung der Bücher ein. Hierbei beschreibt 1 = "LA" , 2 = "Fun Facts" , 3 = "Discord Chat" , 4 = "PTP1" , 5 = "PEP1"
Als nächstes wird die Permutation [math] \sigma [/math] auf die Aufstellung angewandt, wobei
- [math] σ = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 2 & 3 & 1 & 4 & 5 \end{pmatrix} [/math].
Zur Notation der Zweizeilenform: In der ausführlichen Darstellung einer [math] n [/math]-stelligen Permutation [math] \pi [/math] schreibt man diese als Matrix mit zwei Zeilen und [math] n [/math] Spalten. In der oberen Zeile stehen die Zahlen von [math] 1 [/math] bis [math] n [/math] (in beliebiger Reihenfolge). Unter jeder Zahl [math] j\in \{1,...,n\} [/math] steht dann in der zweiten Zeile der Funktionswert [math] \pi(j)[/math] :
[math]
\pi = \begin{pmatrix} 1 & 2 & 3 & ... & n \\ \pi(1) & \pi(2) & \pi(3) & ... & \pi(n) \end{pmatrix}
[/math]
Auch in der zweiten Zeile steht somit jede Zahl von [math] 1 [/math] bis [math] n [/math] genau einmal.
Sei [math] \mu [/math] eine andere Permutation.
Zuletzt wird [math] \mu [/math] auf die bereits von [math] \sigma [/math] permutierte Aufstellung angewandt. Hieraus ergibt sich für die Endaufstellung = [math] \sigma \circ \mu [/math]
- [math] μ = \begin{pmatrix} 1 & 2 & 3 & 4 & 5 \\ 4 & 3 & 5 & 1 & 2 \end{pmatrix} [/math]
Zykelschreibweise
Die Vertauschungen werden häufig in sogenannten "Zykeln" geschrieben. Dabei werden die Positionen die durch die Vertauschungen geändert werden hintereinander in eine Klammer geschrieben. Dementsprechend ist die Zykelschreibweise nicht eindeutig. Die klassische Notation ist in der Klammer aufsteigend.
Die Zykelschreibweise von [math]\sigma[/math] wäre zum Beispiel:
- [math] \sigma = ( 1 ~ 2 ~ 3) (4) (5) = ( 1 ~ 2 ~ 3) [/math]
Dabei werden in der Notation die Zyklen der Länge 1 nicht mitgeschrieben.
Analog zu oben wäre die Schreibweise zu [math]\mu[/math] :
- [math] \mu = ( 1 ~ 4) (2 ~3 ~ 5)[/math]
Zu beachten ist hierbei, dass die Permutationen im Generellen nicht kommutieren:
- [math] \sigma \circ \mu = ( 1 ~ 2 ~ 3) ( 1 ~ 4) (2 ~3 ~ 5)= (1 ~ 4 ~ 2)(3~5) [/math]
- [math] \mu \circ \sigma = ( 1 ~ 4) (2 ~3 ~ 5)( 1 ~ 2 ~ 3)= (1 ~ 3 ~ 4)(2~5) [/math]
- [math]\mapsto \sigma \circ \mu \neq \mu \circ \sigma [/math]
Nice to know: Disjunkte Zykel kommutieren
Signumsabbildung
Die Signumsabbildung ist eine surjektive Abbildung welche eine beliebige Permutation auf [math] 1 [/math] oder [math] -1 [/math] abbildet. Dabei kann man die [math] 1 [/math] so interpretieren, dass die abgebildete Permutation eine gerade Anzahl von Fehlstellen hat. Die [math] -1 [/math] zeigt somit eine ungerade Anzahl von Fehlstellen an.
Als Fehlstelle versteht man in diesem Kontext, dass ein Element welches vorher hinter einem anderen Element platziert war, durch die Permutation vor das andere Element gezogen wurde. Ein Beispiel für eine Permutation mit zwei Fehlstellen wäre:
- [math] \mu = ( 1 ~ 2 ~ 3) \longrightarrow sgn(\mu) = +1 [/math]
In diesem Beispiel entsteht die Fehlstelle dadurch, dass die [math] 3 [/math] "vor" die [math] 1 [/math] und [math] 2 [/math] geschoben wird.
Für eine generelle Berechnung der Fehlstellen für [math] \pi \in S_n [/math] kann die Formel:
- [math]sgn(\pi) = \prod_{1 \leq i\lt j \leq n} \frac{\pi(j)-\pi(i)}{j-i}[/math]
genutzt werden.[2]
Die Abbildung : [math]sgn: S_n \mapsto \{ \pm 1 \}[/math] ist dabei ein Gruppenhomomorphismus.
Alternierende Gruppe
Die alternierende Gruppe vom Grad [math]n[/math] ist eine Untergruppe der symmetrischen Gruppe [math]S_n[/math]. Sie besteht aus allen gerad-anzahligen Permutationen einer [math]n[/math]-elementigen Menge.
Sie ist definiert als:
[math]A_n[/math] := [math]\{\sigma \in S_n |sgn(\sigma)=1\} \subset S_n [/math].
Die Verknüpfung der alternierenden Gruppe ist, wie auch die der symmetrischen Gruppe, die Verkettung (Hintereinanderausführung) der Permutationen.
Lemma: [math]A_n[/math] wird erzeugt von Zykeln der Form [math](12i)[/math] mit [math]i \in \{3,...,n\}[/math] mit [math]n \geq 3[/math].
D.h. für jedes [math]\sigma \in A_n[/math] gibt es eine Darstellung [math]\sigma = (12i_1)(12i_2)...(12i_k)[/math] mit [math]i_1 ...i_k \in \{3,...,k\}[/math].
Anwendung auf den Zauberwürfel
Notation
Gruppeneigenschaften
Sowohl bei der Betrachtung der Würfelecken, als auch der Würfelkanten stellt, jede Drehung (jeweils im mathematisch negativen Sinn) einer der Würfelscheiben eine zyklische Permutation dar, die als Element der symmetrischen Gruppe [math]S_8[/math] (für die Permutionen der Eckwürfelchen), oder [math]S_{12}[/math] (für die Permutationen der Kanten), aufgefasst werden kann. Jede mögliche Würfeldrehung ist dabei als Zusammensetzung von Verknüpfungen der genannten sechs Grundpermutationen [math]\{V,H,R,L,O,U\}[/math] darstellbar.[4]
Sei [math]G[/math] die Menge aller möglichen Drehoperationen am Zauberwürfel. Mit der Verknüpfung "[math]\circ[/math]"[math]: G \times G \rightarrow G [/math] wird [math]G[/math] eine Gruppe:
- Die Abgeschlossenheit durch die Verknüpfung "[math]\circ[/math]" der Gruppenelemente ist gegeben.
- Da auf Elemente aus [math]S_n, n \in \{8,12\}[/math] zurückgegriffen wird, gilt das Assoziativgesetz.
- Das neutrale Element [math]e_n, n \in \{8,12\}[/math] ist die Nulloperation, also das Nicht-Verdrehen des Würfels, sodass gilt: [math]\forall g \in G: g \circ e_n = e_n \circ g =g [/math]
- Es existiert ein eindeutiges Inverses [math]g^{-1}[/math]zu jedem [math] g \in G : g \circ g^{-1} = g^{-1} \circ g = e_n [/math]. Für die Grundpermutationen ist dies anschaulich jeweils die Rückdrehung im mathematischen Uhrzeigersinn.
Die Gruppe [math]G[/math] ist nicht abelsch; so ist beispielsweise [math]V \circ L \neq L \circ V [/math].
Ordnung
Die Ordnung der Gruppe G ergibt sich aus der Anzahl [math]\vert G \vert[/math] der möglichen Drehoperationen. Zu deren Bestimmung ist die natürliche Bijektion zwischen der Gruppe [math]G[/math] und der Menge aller möglichen, durch ein [math]g \in G[/math] erreichten, Würfelpositionen nützlich:
Die Würfelposition kann eindeutig durch den Positionsvektor [math](\rho, \sigma, x, y) \in S_8 \times S_{12} \times (\mathbb{Z} / 3\mathbb{Z})^8 \times (\mathbb{Z} / 2\mathbb{Z})^{12} [/math] dargestellt werden. Dabei zeigt [math]\rho \in S_8[/math] die Permutation der Eckwürfelchen, [math]\sigma \in S_{12} [/math] die Permutation der Kanten, [math]x \in (\mathbb{Z} / 3\mathbb{Z})^8[/math] die Orientierung der Eckwürfelchen und [math]y \in (\mathbb{Z} / 2\mathbb{Z})^{12} [/math]die Orientierung der Kanten, jeweils ausgehend von der Grundstellung, an. [5]
Orientierung
Die angesprochenen Orientierungen sind dabei folgendermaßen definiert:
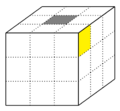
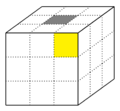
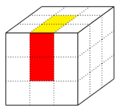
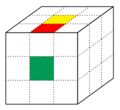
Für die Orientierung der Ecken wird die Tatsache verwendet, dass jeder Eckwürfel genau eine gelbe oder weiße Seite hat. Ist diese Seite auf der Deckenfläche (diese wird so gewählt, dass sich eine weiße oder gelbe Teilfläche (im Bild als grau dargestellt) auf der mittleren Position befindet) positioniert, so wird der Orientierung die Äquivalenzklasse der [math][0][/math] zugeordnet. Ist sie von dort aus entgegen des mathematischen Sinns zur Seite gedreht, wird ihr die [math][1][/math] zugeordnet, und ist sie von dort aus, aus Sicht der angrenzenden Seitenfläche, im mathematischen Sinn nach vorne gedreht, die [math][2][/math]. Wird dies für jedes der acht Eckwürfelchen [math]x_i, i \in \{1, \ldots, 8\}[/math]durchgeführt, erhält man den Orientierungsvektor [math]x=(x_1, \ldots, x_8) \in (\mathbb{Z} / 3\mathbb{Z})^8 [/math]. Dies wird an den folgenden Abbildungen ersichtlich:
Orientierung einer Ecke als Äquivalenzklasse der [math][0][/math]
Orientierung einer Ecke als Äquivalenzklasse der [math][1][/math]
Orientierung einer Ecke als Äquivalenzklasse der [math][2][/math]
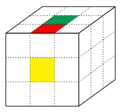
Für die Orientierung der Kanten verwendet man, dass jede Kante zwei Farben aus zwei verschiedenen Farbgruppen [math]([/math]diese sind gelb/weiß [math](ge/w)[/math], grün/blau ([math](gr/b)[/math], rot/orange [math](r/o))[/math] besitzt. Stellt man die Farbauswahl schematisch als [math](ge / w \,\,\,\, gr / b \,\,\,\, r / o\,\,\,\, ge / w \,\,\,\, gr / b)[/math] dar, so kann man eine Auswahl für die beiden möglichen Orientierungen der Kante wie folgt treffen: Man vergleicht jeweils die Farben der Mittelwürfelchen und der direkt aufeinandertreffenden Seitenwürfelchen der Zauberwürfelseiten, zwischen denen die gewünschte Kante liegt. Anschließend bestimmt man, je für die beiden Mittelwürfelchen und dann für die Seitenwürfelchen, in welcher Richtung die dargebotene Farbe des Vorderseitenwürfels aus der des Oberseitenwürfels aus dem Schema [math](ge / w \,\,\,\, gr / b \,\,\,\, r / o\,\,\,\, ge / w \,\,\,\, gr / b)[/math] hervorgeht, also ob die Folgerichtung rechts oder links ist. Stimmen die Richtungen auf den Feldern derselben Zauberwürfelseite überein, so entspricht die Kantenorientierung der Äquivalenzklasse der [math][0][/math], ansonsten der der [math][1][/math]. Dies wird anhand der folgenden Beispiele verdeutlicht:
Orientierung einer Kante als Äquivalenzklasse der [math][0][/math]
Orientierung einer Kante als Äquivalenzklasse der [math][0][/math]
Orientierung einer Kante als Äquivalenzklasse der [math][1][/math]
Die Ordnung von [math]G[/math] ergibt sich nun aus der Anzahl der möglichen Positionen der Eckwürfel, der Kantenwürfel, sowie der möglichen Orientierungen der Ecken und Kanten und den Aspekten des Lösbarkeitssatzes [6]als
[math]\vert G \vert = \frac{8!\cdot 12!\cdot 3^8\cdot 2^{12}}{2 \cdot 2 \cdot3} = 43\,\,\, 252\,\,\, 003\,\,\, 274\,\,\, 489\,\,\, 856\,\,\, 000 [/math][7]
Mögliche Untergruppen
Eine recht einfache Oberkategorie möglicher Untergruppen am Zauberwürfel ist durch die sogenannten zyklischen Untergruppen gegeben. Das sind jene Untergruppen, die sich nur aus einem einzigen [math]g \in G [/math] und dessen Verknüpfungen zusammensetzten. Ein Beispiel hierfür ist etwa die Teilmenge der Drehungen der oberen Würfelscheibe entgegen des mathematisch negativen Sinnes [math]\{O\} \subset G [/math] mit der Verknüpfung "[math]\circ[/math]".
Das neutrale Element ist enthalten durch [math] e = O^4 \in (\{O\},\circ)[/math] und somit gilt auch [math] O \circ O^{-1}=e \in (\{O\},\circ) [/math].
Weitere Beispiele für Untergruppen sind die orientierungserhaltende Untergruppe [math] G_1 := \{g=(\rho, \sigma, x, y) \in G| x=0, y=0\} [/math]
und die, nur die Orientierung ändernde, Untergruppe [math] G_2 := \{g=(\rho, \sigma, x, y) \in G| \rho=1, \sigma=1\} [/math].[8]
Der 3x3 Zauberwürfel
Eigenschaften
- 27 kleien cubies
- 6 mittleren cubies
- 12 Kantencubies
- 8 Eckcubies
- 6 verdrehbare Seiten, 27-6 verdrehbare Cubies
→ 43*10^18 Möglichkeiten den Würfel zu verdrehen
[math]10^{18}[/math]
Lösungsstrategie
Weitere Zauberwürfel
2x2 Zauberwürfel
.... Form des Zauberwürfels
Quellen
- ↑ https://de.wikipedia.org/wiki/Symmetrische_Gruppe
- ↑ https://mampf.mathi.uni-heidelberg.de/mediaforward/medium/16609/manuscript/ef7c2209ceb055a6c08e459784dca941.pdf
- ↑ Bearbeitung erfolgt durch die Gruppe "Lösungsstrategien am Zauberwürfel".
- ↑ Christoph Bandelow: Inside rubik’s cube and beyond, Boston, 1982, ISBN 978-0-8176-3078-2
- ↑ Christoph Bandelow: Inside rubik’s cube and beyond, Boston, 1982, ISBN 978-0-8176-3078-2
- ↑ Erläuterung erfolgt durch die Gruppe "Lösungsstrategien am Zauberwürfel".
- ↑ https://mampf.mathi.uni-heidelberg.de/mediaforward/medium/16609/manuscript/ef7c2209ceb055a6c08e459784dca941.pdf
- ↑ Christoph Bandelow: Inside rubik’s cube and beyond, Boston, 1982, ISBN 978-0-8176-3078-2