Banach-Tarski-Paradox

Verdopplung eines Balles nach Banach-Tarski.

Das Banach-Tarski-Paradoxon (eng. Banach-Tarski-Paradox) oder auch Satz von Banach und Tarski ist ein Satz aus der geometrische Mengenlehre, welcher die Grenzen des anschaulichen Volumenbegriffs deutlich macht. Nach dem Satz gegeben eine Kugel in drei oder mehr Dimensionen, existiert eine Zerlgung der Kugel in endlich viele disjunkte Teilmengen bzw. Teilen, sodass sich aus den Teilen zwei Kugeln des selben Radius als die ursprüngliche Kugel konstruieren lassen. Dadurch verdoppelt sich das Volumen unersichtlich (denn eine Kugel wurde in zwei genauso große zerteilt). Dieses Paradoxon veranschaulicht somit, dass das mathematische Modell des Raumes in der Mathematik die Realität nicht an allen Eigenschaften wiederspiegelt.

Im Gegensatz zu vielen anderen Sätzen aus der Geometrie ist der Banch-Tarski Satz ziemlich abhängig von der Wahl der Axiomen. Das Axiom der Wahl (eng. Axiom of Choice) erlaubt für einen Beweis, da überabzählbar viele Wähle getroffen werden müssen. Dies folgt aus der Natur der Teilmengen in welche man den Ball zerlegt, diese sind nämlich unednlich filigran bzw. staubwolkenartig (siehe Löwenzahn^[1]). Eine andere Auswahl an Axiomen gibt es aber, sodass eine solche Zerlegung und Rekonstruktion der Kugel nicht möglich sind.

Vorwissen

Hilberts Hotel

Hilberts Hotel (eng. Hilbert's Paradox of the Grand Hotel) ist ein Gedankenexperiment, erschaffen von David Hilbert und eingeführt in seiner Vorlesung "Über das Unendliche" im Jahre 1924. Es demonstriert die konterintuitiven Eigenschaften des Unendlichen, wie z.B. die Eigenschaft, dass ein Hotel mit unendlichen Räumen und einem Gast pro Raum nicht voll besetzt ist und weitere Gäste problemlos einen Raum zugewiesen kriegen können, oder die uns wichtigere Eigenschaft, dass, wenn ein Gast das Hotel verlässt, alle anderen Gäste so umgeschoben werden können, dass wieder jeder Raum besetzt ist und das Hotel scheinbar wieder vollgebucht ist.

Da Hilberts Hotel in der Vorlesung besprochen wurde und auch schon von einer anderen Gruppe behandelt wird, werden wir den Artikel Hilberts Hotel hier verlinken.

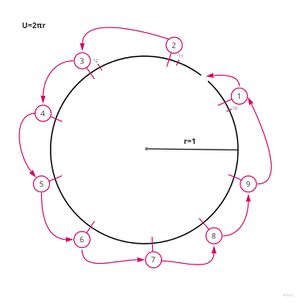
In einem Kreis lassen sich abzählbar viele Lücken füllen nur durch das Umordnen der existierenden Punkten.

Hilberts Hotel kann auch auf Formen angewandt werden. Wenn man aus einem Kreis einen einzigen Punkt entfernt^[2], entsteht scheinbar eine Lücke. Da aber der Umpfang eines Kreises immer irrational ist, kann man einfach von der Lücke aus entlang dem Umpfang Strecken von einer rationalen Länge abmessen und den entsprechenden Punkt markieren (den ersten mit 1, den zweiten mit 2 etc.). Am Ende des Prozesses hat man unendlich viele Punkte markiert, mit denen man entsprechend Hilberts Hotel die Lücke einfüllen kann: Punkt 1 füllt die Lücke, Punkt 2 füllt die Lücke, die durch Punkt 1 entstanden ist und so weiter. Somit ist also Hilberts Hotel auch anwendbar auf Formen und Körper.

Hyperwebster

Der Hyperwebster ist eine Erfindung von Dr Ian Steward, um zu veranschaulichen, wie groß unzählbare Unendlichkeit sein kann.

Der Hyperwebster ist eine Version von Webster's Dictionary, wo jede mögliche Buchstabenkombination vorkommen soll. Man starte mit dem Buchstaben A, dann AA, dann AAA, und so weiter bis man unendlich viele A's hat. Danach kommt AB, ABA, ABAA, ABAAA, ..., AC, ..., AZ, ..., B, BA, BAA, ..., Z, ZA, ZAA etc. Am Ende sieht der Hyperwebster dann ungefähr so aus:

A, AA, AAA, AAAA, ..., AB, ABA, ABAA, .... AAB, AABA, ..., AC, ... AZ, AZAA, ...

B, BA, BAA, ..., BB, BBA, ..., BZ, BZA, ...

...

Z, ZA, ZAA, ..., ZB, ZBA, ..., ZZZZZZZZZZZZZZZ...

Nun haben wir ein Wörterbuch, welches jedes mögliche Wort, jeden möglichen Satz, jede mögliche Buchstabenkombination enthält. Der Verlag möchte jetzt dieses Wörterbuch ausdrucken, es wäre aber viel zu groß. Der Verlag fasst also alle Wörter in 26 Bände zusammen, somit werden alle Wörter mit einem bestimmten Anfangsbuchstaben in einen Band gepackt.

Um jetzt Platz zu sparen, nimmt der Verlag jeden Band und streicht den Anfangsbuchstaben jedes Wortes, da jeder Anfangsbuchstabe nur ein Mal pro Band vorkommt. Dabei stellt sich heraus, dass, wenn man den Anfangsbuchstaben jedes Bandes kürzt, man wieder den Hyperwebster selbst erhält. Der Hyperwebster ist also in diesem Sinne ein sich selbst enthaltendes Fraktal, da man durch die oben beschriebene Methode aus einem Hyperwebster gleich 26 machen kann.

Paradox

Der Banach-Tarski Satz widerspricht die gängliche geometrische Intuition und wird somit oft auch Banach-Tarski Paradoxon genannt. Nach Banach-Tarski wird ein Ball in zwei weitere Bälle mit demselben Volumen zerlegt ohne den Ball zu dehnen, biegen oder neue Punkte dem Ball zuzufügen, tatsächlich werden die Teile, in welche der Ball zerlegt wird, nur rotiert und geschoben (entspricht eine Translation in der Mathematik). Es scheint unmöglich zu sein, durch diese Operationen das Volumen zu erhöhen, da sie, intuitiv betrachtet, das Volumen erhalten. Mathematisch ist es auch oft so nun kann man dieselbe Intuition bei dieser Zerlegung des Balles nicht anwenden da für die Teile in welche der Ball zerlegt wird, kein Volumen definiert werden kann.

Man kann sich die Teile in welche der Ball zerlegt wird jeweils als eine reife Löwenzahnpflanze vorstellen. Also, mathematisch gesehen, eine Sammlung an Punkten um einen Mittelpunkt zusammen mit dem Liniensegment, welcher den Punkt zum Mittelpunkt verbindet. Ein solches Konstrukt existiert in 3 Dimensionen hat aber kein Volumen.

Nach dem Widerzusammenfügen der Teile lässt sich wieder ein Volumen definieren und nun ist es so dass das Volumen anders als das urspüngliche Volumen ist (nämlich doppelt so groß). In der Realität lassen sich solche Umformungen leider nicht durchführen da der Ball in unendlich feine bzw. dünne Teile zerlegt wird.

Eine allgemeinere Version des Satzes existiert, oft informell "pea and the Sun paradox" (dt. Das Erbse-Sonne Paradoxon) genannt, besagt er dass eine Erbse in Stücke zerlegt werden kann und dass sich aus den entstehenden Stücken dann die Sonne kontruieren lässt.

Geschichte, Banach und Tarski

In einem in 1924 veröffentlichem Paper gaben Stefan Banach und Alfred Tarski eine Konstruktion einer solchen paradoxischen Zerlegung, gegründet in der früheren Arbeit von Giuseppe Vitali. Banach und Tarski haben den folgenden, allgemeineren (auch stärkeren) Satz bewiesen:

Sei [math]d \ge 3[/math] eine ganze Zahl und seien [math]X, Y\subset \mathbb{R}^d[/math] beschränkte Mengen mit nicht-leerem Inneren. Dann gibt es eine natürliche Zahl [math]n[/math] und eine disjunkte Zerlegung [math]X_1, \dots, X_n[/math] von [math]X[/math] und zugehörige Bewegung [math]\beta_1, \dots, \beta_n[/math] derart, dass [math]Y[/math] die disjunkte Vereinigung der Mengen [math]\beta_1(X_1), \dots, \beta_n(X_n)[/math] ist.

Das heißt in [math]\mathbb{R}^d:d\geq 3[/math] lässt sich eine beschränkte Menge mit nicht-leerem Inneren disjunkt zerelegen und dann in eine belibiege, beschränkte Menge mit nicht-leerem Inneren wieder disjunkt vereineigen. Da wir die durch die Zerlegung konstruierte Teilmenge nur bewegen, werden keine neue Punkten erzeugt und die Abstände zwischen allen Punkten werden paarweise erhalten. Somit folgt das Banach-Tarski Paradoxon als ein bestimmter Fall: Sei die Menge [math]X[/math] von oben ein Ball und die Menge [math]Y[/math] zwei Kopien des Balles mit denselben Radius als der Ball [math]X[/math]. Dann gilt: [math]X,Y\subset \mathbb{R^3}[/math], da Bälle per definition beschränkt sind und ein nichtleeres Innere haben. Gilt nach dem Satz dass eine disjunkte Zerlegung [math]X_1,..., X_n[/math] von [math]X[/math] zusammen mit der zugehörigen Bewegung [math]\beta _1,..., \beta _n[/math] existiert sodass [math]Y=\beta _1(X_1)\cup \beta _2(X_2)\ \cup ... \cup\ \beta _n(X_n)[/math] gilt.

Der allgemeinere Satz von Banach und Tarski gilt in einer und zwei Dimensionen nicht, denn die Bewegungsfreiheit in diesen Dimensionen zu beschränkt ist. Als Folge dessen besitzen alle Figuren, welche durch eine Zerlegung und eine zugehörige Bewegung der Teile, sich ineinander umformen lassen, denselben Flächeninhalt. Banach und Tarski haben aber gezeigt dass, wenn Zerlegungen in abzählbar viele Teile (statt endlich viele) erlaubt sind, die analoge Version des Satzes immer noch gilt.

Beweisskizze

Anmerkung: hier erklären wir bloß die Grundzüge des Beweises, eine ausführlichere Beweisskizze finden Sie hier.

Der Beweis benutzt die Tatsache dass Drehungen im Raum mathematisch als Elemente einer Gruppe aufgefasst werden können. Somit kann man die miteinander verknüpfen und auf andere Objekte anwenden, wobei die Bedingungen der Gruppe erfüllt sind:

Die Verknüpfung mehrerer Drehungen ist wiederum eine Drehung.
Die Verknüpfungsoperation ist assoziativ.
In einer Verknüpfungskette [math] g_1\dots\ g_i g_i^{-1}\dots\ g_n g_1\dots\ g_ig_i^{-1}\dots\ g_n [/math] eliminieren sich die benachbarten Elemente [math] g_{i}g_{i} [/math] und [math] g_{i}^{-1}g_i^{-1} [/math] da sie zueinander invers sind. Dies gilt für Drehungen ebenso. Drehungen operieren auf Punkten oder Punktmengen im Raum, indem sie deren Lage verändern.

Für den Beweis wird eine ganz besondere Gruppe betrachtet; Die freie Gruppe [math]F_2[/math] mit ihren Erzeugern [math]a[/math] und [math]b[/math] besteht abstrakt definiert aus Wörtern über dem Alphabet (Alphabete sind Mengen von Buchstaben) [math]E:=\{a,a^{-1},b,b^{-1}\}[/math], in denen keine Inversen benachbart sind. Die Verknüpfung der Gruppe stellt die Konkatenation dar, wobei möglicherweise entstandene Invers-Paare iterativ entfernt werden, bis keine solchen Paare im verknüpften Wort mehr vorkommen. Das leere Wort [math]\varepsilon[/math] stellt das neutrale Element der Gruppe dar. Die Darstellung jedes Elements von [math]F_2[/math] als gekürztes Wort ist dabei eindeutig.

Schritt I

Wir definieren die Mengen [math]S(a), S(b), S(a^{-1}), S(b^{-1})[/math]. Hier ist [math]S(a)[/math] die Menge aller Wörter aus [math]F_2[/math], die links mit [math]a[/math] beginnen, z.Bs.: [math]ab, abb,aba^{-1}[/math]. Die anderen S-Mengen sind analog definiert. Wir fordern wir oben dass die Darstellung der Wörter gekürzt ist, aslo [math]a[/math] und [math]a^{-1}[/math] kommen nicht nebeneinander vor, [math]aa^{-1}[/math] ist nicht erlaubt!

Schritt II

Wie zeigen dass eine paradoxe Zerlegung von [math]F_2[/math] existiert. Neben der üblichen Zerlegung: [math]F_2={e}\cup S(a)\cup S(a^{-1})\cup S(b)\cup S(b^{-1})[/math] gelten auch die folgende Zerlegungen: [math]F_2=aS(a^{-1})\cup S(a)[/math], und [math]F_2=bS(b^{-1})\cup S(b)[/math],
denn
[math]aS(a^{-1}):=\{ax|x\in S(a^{-1}) \}=\{aa^{-1} \}\cup \{ax|x=a^{-1}g_0...,a\neq g_0\in E \}[/math]

[math]=\{e \}\cup \{aa^{-1}g_0...|a\neq g_0\in E \}=\{e \}\cup S(b)\cup S(b^{-1})\cup S(a^{-1})[/math]

und
[math]bS(b^{-1}):=\{bx|x\in S(b^{-1}) \}=\{bb^{-1} \}\cup \{bx|x=b^{-1}g_0...,b\neq g_0\in E \}[/math]

[math]=\{e \}\cup \{bb^{-1}g_0...|b\neq g_0\in E \}=\{e \}\cup S(a)\cup S(b^{-1})\cup S(a^{-1})[/math].

Jetzt haben wir [math]F_2[/math] paradox zerlegt. Dass heißt wir haben aus einer disjunkter Zerlegung zwei Kopien von der Gruppe erzeugt (bzw. der Menge an Wörtern). Dabei haben wir keine neue Wörter erzeugt sondern nur die bereits in den Teilmengen enthaltenen Wörter durch die Gruppenverknüpfgung modifiziert: von [math]S(a^{-1})[/math] zu [math]aS(a^{-1})[/math]. Jetzt benutzten wir diese Zerlegung für die Verdoppelung des Balles.

Schritt III

Dafür müssen wir eine Menge von Drehungen mit der [math]F_2[/math] Gruppe identifizieren. Dafür ist es notwendig dass diese Menge unendlich viele Elemente besitzt, denn [math]F_2[/math] besitzt auch unendlich viele Elementen. Die Gruppe der Drehungen um 120° ist somit kein gültiger Kandidat, denn sie enthält nur drei Elementen: nach einer dreifachen Drehung um 120° erreicht man die Ausgangsposition. Drehen wir um einen irrationalen Bruchteil von [math]\pi[/math], z. B. mit [math]\theta =\arccos \left({\tfrac {1}{3}}\right)[/math], und sei [math]a[/math] eine entsprechende Drehung um die x-Achse, sowie [math]b[/math] eine um die y-Achse, dann lässt sich zeigen, dass die dabei erzeugte Gruppe isomorph zu [math]F_2[/math] ist. Wir nennen sie [math]H[/math].

Schritt IV

[HIER KOMMT NOCH WAS]

Implikationen des Paradoxons im echten Leben

Verschwindende Schokolade

Ein Beispiel für eine "Anwendung" des Banach-Tarski-Paradoxons in der Realität ist das Phänomen der "verschwindenden" Schokolade, welches in multiplen Videos über Social Media verbreitet wurde. Ähnlich wie auch bei Banach-Tarski geht es um ein Objekt, welches in unterschiedliche Teile zerlegt wurde, so zusammen zu setzen, dass man wieder das ursprüngliche Objekt erhält, dabei jedoch eines der Teile weg gelassen werden kann.

Besteht eine Schokoladentafel zum Beispiel aus 4 mal 8 einzelnen Stückchen, so lässt sich die Tafel auf eine bestimmte Weise zerschneiden, sodass sie beim erneuten Zusammensetzen wieder die ursprünglichen 4 mal 8 Stückchen enthält. Eines der Stückchen ist jedoch beim Zusammensetzen übrig geblieben und doch scheint es so als hätte die Schokoladentafel immer noch ihre ursprüngliche Größe.

Realistisch ist die Schokoladentafel um genau das herausgeschnittene Stückchen kürzer, was bedeutet, dass nicht mehr alle Stückchen der Tafel die selbe Größe haben.

Hadron Physics and Transfinite Set Theory

Hadronen sind in der Physik subatomare Teilchen, die durch starke Wechselwirkung zusammengehalten werden. Die bekanntesten sind Protonen und Neutronen, also die Bestandteile von Atomkernen. Die Hadron Physics and Transfinite Set Theorie, welche erstmals von B.W.Augenstein 1984 veröffentlicht wurde, basiert auf der Quark-Theorie. Laut dieser bestehen Hadronen aus sehr viel kleineren Quarks. Die mathematische Verbindung zwischen dem Banach-Tarski-Paradoxon und dieser Theorie der Quantenphysik stellen die nicht-abelschen Gruppen dar, welche in der Hadronenphysik und in paradoxen Zerlegungen eine essenzielle Rolle spielen.

Das von uns gewählte Paradoxon beschreibt grob gesagt eine Kugel, welche sich in mbeispielsweise fünf Teile zerlegen lässt. Drei dieser Teile ergeben eine Kopie der ursprünglichen Kugel, die zwei restlichen Teile ergeben eine zweite Kopie. Die Kugel könnte nun als ein Hadron aufgefasst werden und die einzelnen Bruchstücke als Quarks. Zerfällt nun ein fünf-Quark Hadron in einzelne Quarks, so kann daraus theoretisch ein zwei-Quark Hadron und ein drei-Quark Hadron zusammen gesetzt werden.

Bisher gibt es keine Experimente, die mit dieser Theorie unvereinbar wären.

[math][/math]

Quellen

[1] ttps://funfacts.mathi.uni-heidelberg.de/index.php/Datei:Dandelion_(107276119).jpg

[2] ttps://funfacts.mathi.uni-heidelberg.de/index.php/Datei:Circle_graphic.jpg

[3] ttps://en.wikipedia.org/wiki/Banach%E2%80%93Tarski_paradox#Obtaining_infinitely_many_balls_from_one

[1]

[2]

[3]