Surreale Zahlen

Surreale Zahlen wurden zunächst von John Conway vorgestellt, der sie zunächst einfach "Zahlen" (engl. Numbers) nannte, Bekanntheit erlangten sie 1974 durch den in Dialogform verfassten Roman Surreal Numbers: How Two Ex-Students Turned on to Pure Mathematics and Found Total Happiness von Donald E. Knuth. Dieser benutzte dabei den Begriff der Surrealen Zahlen, den auch Conway später verwendete. Surreale Zahlen lassen sich allein aus dem Vorhandensein von Mengen konstruieren, sind aber selbst nur eine Klasse. Sie enthalten die reellen und auch hyperreellen Zahlen als Teilmenge. Desweiteren eignen sie sich zur spieltheoretischen Analyse von bestimmten Spielen.

Erste Konstruktionsschritte

Grundidee

jede surreale Zahl [math]x [/math] lässt sich als [math]x = \{L|R\} [/math] mit zwei Mengen [math]L [/math] (linke Menge von [math]x [/math]) und [math]R [/math] (rechte Menge von [math]x [/math]) schreiben, wobei gelten soll:

• [math]L [/math] und [math]R [/math] sind selber Mengen surrealer Zahlen oder die leere Menge
• Wohlgeformtheit: Jedes Element aus [math]L [/math] ist kleiner als jedes Element aus [math]R [/math] (siehe Ordnungsrelation)

Die so entstandene Zahl [math]x [/math] ist größer als jedes Element aus [math]L [/math] und kleiner als jedes Element aus [math]R [/math].

Rekursiv werden dann weitere surreale Zahlen erzeugt, die einzelnen Rekursionsschritte bezeichnet man dabei mit Tagen, beginnend mit Tag 0. Der Tag, an dem eine surreale Zahl erzeugt wird, nennt man den Geburtstag dieser Zahl.

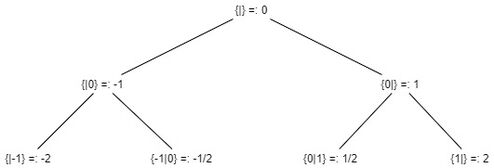
Wir betrachten die Äquivalenzrelation: [math]x == y :⇔ x ≤ y [/math] und [math]y ≤ x [/math] (Die Definition der Äquivalenzklassen ist rein rekursiv) und geben den entsprechenden Äquivalenzklassen der Form [math][x] [/math] neue Bezeichnungen, wobei als Repräsentant das älteste Mitglied der Äquivalenzklasse gewählt wird (also das, welches als erstes gezeugt wurde und somit den frühesten Geburtstag hat, siehe Abbildung zu Tag 0 bis Tag 2)

Notation

Wir schreiben der Einfachheit und Übersichtlichkeit halber [math]\{a,b|x\} [/math] statt [math]\{\{a,b\}|\{x\}\} [/math] und [math]\{|y\} [/math] statt [math]\{∅|\{y\}\} [/math].

Ordnungsrelation

Seien [math]x = \{L_x|R_x\}[/math], [math]y = \{L_y|R_y\}[/math] surreale Zahlen.

Dann gilt [math]x ≤ y[/math] genau dann, wenn [math]y[/math] kleinergleich keinem Element von [math]L_x[/math] und kein Element von [math]R_y[/math]kleinergleich [math]x[/math] ist. [math]x \lt y[/math] wird als "nicht [math]y ≤ x[/math]" definiert.

(Quantorenschreibweise: [math]x ≤ y :⇔ ∀l_x∈L_x: l_x \lt y, ∀r_y∈R_y: r_y \gt x[/math]

Bemerkung: Diese Definition ist zunächst etwas verwirrend, weil für die Definition der ≤-Relation die ≤-Relation bereits selber verwendet wird. Die Relation ist also rein rekursiv gegeben.

Beispiel:

( [math]0[/math] bezeichnet [math]\{|\}[/math], [math]-1[/math] bezeichnet [math]\{|0\}[/math], mehr dazu: siehe unten) zeige, dass [math]-1 \lt 0[/math]: [math]-1 \lt 0[/math] [math]⇔ \{|0\} \lt \{|\}[/math] [math]⇔ ¬(\{|\} ≤ \{|0\})[/math] [math]⇔ ¬(∀l_x∈∅: l_x \lt \{|0\} [/math] und [math]∀r_y∈\{0\}: r_y \gt \{|\}) [/math] [math]⇔ ¬(∀r_y∈\{0\}: r_y \gt \{|\})[/math] [math]⇔ ∃r_y∈\{0\}: r_y ≤ \{|\}[/math] [math]⇔ 0 ≤ 0[/math] (✓)

Tag 0 bis zur Unendlichkeit

So lassen sich die ersten surrealen Zahlen konstruieren:

Wähle für die linke und rechte Menge der neuen surrealen Zahl Mengen bereits bekannter surrealer Zahlen bzw. die leere Menge. Überprüfe dann, ob die so entstandenen Zahlen wohlgeformt sind. Falls ja, betrachte die Äquivalenzklassen bezüglich der Gleichheitsrelation und benenne sie neu (Schema zur neuen Bezeichnung: siehe Abbildung)

(Bemerkung: Die Notation ist zunächst etwas verwirrend, da zum Beispiel [math]0[/math] sowohl die surreale Zahl [math]\{|\}[/math]als auch deren Äquivalenzklasse bezeichnet. Diese Überladung wird dadurch aufgelöst, dass bezüglich der ==-Relation äquivalente Zahlen nicht mehr einzeln betrachtet werden.)

(Bemerkung: warum die Bezeichnungen genau so gewählt sind, ergibt sich erst wirklich, wenn die surrealen Zahlen als Körper betrachtet werden. Dazu werden die arithmetischen Verknüpfungen im Abschnitt "Rechnen mit surrealen Zahlen" definiert. )

Tag 0

Wir beginnen mit der leeren Menge als rechte sowie linke Menge. Da die leere Menge keine Elemente enthält, wird keine Regel verletzt und wir erhalten die wohlgeformte surreale Zahl [math]\{|\}[/math], die wir (wie auch ihre Äquivalenzklasse) [math]0[/math] nennen.

/

Tag 1

Nun können wir aus der leeren Menge und unserer ersten surrealen Zahl [math]0[/math] folgende weitere surreale Zahlen konstruieren: [math]\{|0\} := -1[/math] und [math]\{0|\} := 1[/math]. Die Zahl [math]\{0|0\}[/math] ist dabei nicht wohlgeformt, da alle Elemente der linken Menge strikt kleiner als alle Elemente der rechten Menge sein müssen und [math]0 ≤ 0[/math] gilt. Es ergibt sich die Anordnung [math]-1 \lt 0 \lt 1[/math].

/

Tag 2

An Tag 2 betrachten wir alle surrealen Zahlen, die wir mit der leeren Menge und unseren surrealen Zahlen [math]-1[/math], [math]0[/math] und [math]1[/math] erzeugen können. Dabei ergeben sich neben unzulässigen Zahlen wie [math]\{0|-1\}[/math] auch die wohlgeformten surrealen Zahlen [math]\{ |-1\}:=-2 \lt -1 \lt \{-1|0\}:=-\frac{1}{2} \lt 0 \lt \{0|1\}:=\frac{1}{2} \lt 1 \lt \{1|\}:=2[/math] Es ergeben sich auch surreale Zahlen, die in bereits bekannten Äquivalenzklassen sind wie [math]\{-1|1\} == 0[/math]. erläutert: [math]\{-1|1\} == 0[/math] . [math]⇔ \{-1|1\} \lt = 0 [/math] und [math]0 \lt = \{-1|1\}[/math] [math]⇔ \{-1|1\} \lt = \{ | \} [/math] und [math]\{ | \} \lt = \{-1|1\} [/math] [math]⇔ \{-1|1\} \lt = \{ | \} [/math] und [math]\{ | \} \lt = \{-1|1\} [/math] [math]⇔ ∀l_x∈\{-1\}: l_x \lt \{|\}, ∀r_y∈∅: r_y \gt \{-1|1\}) [/math] und [math]∀l_x∈∅: l_x \lt \{-1|1\}, ∀r_y∈\{1\}: r_y \gt \{|\})[/math] [math]⇔ -1 \lt 0 [/math] und [math]1 \gt 0[/math](✓) An Tag zwei umfassen die neu erzeugten Äquivalenzklassen gleich zu Beginn mehrere Elemente, z.B gilt [math]\{0,1|\}[/math], [math]\{-1,1|\}[/math], [math]\{-1,0,1|\} ∈ [\{1|\}] = 2[/math]

/

Dieses Muster wird weiter fortgeführt, allgemein gilt:

Sind die Zahlen am n-ten Tag [math]−x_m \lt −x_{m−1} \lt · · · \lt −x_2 \lt −x_1 \lt x_0 = 0 \lt x_1 \lt x_2 \lt · · · \lt x_{m−1} \lt x_m[/math],

so entstehen an Tag n+1 die weiteren Zahlen [math]\{|−x_m\} \lt \{−x_m|−x_{m−1}\} \lt · · · \lt \{−x_2|−x_1\} \lt \{−x_1|0\} \lt \{0|x_1\} \lt \{x_1|x_2\} \lt · · · \lt \{x_{m−1}|x_m\} \lt \{x_m|\}[/math],

wobei alle Zahlen an Tag n+1 sowie an allen vorhergehenden der Form [math]\frac{m}{2^n} [/math] mit [math]m,n \in \mathbb{Z} [/math] sind

Tag ω und danach

Konstruktion von reellen Zahlen

Alle Zahlen, die wir durch Induktion über n erhalten haben, besitzen die Form [math]\frac{m}{2^n}, m,n \in \mathbb{Z} [/math]. Alle diese Zahlen haben endliche Dezimaldarstellungen. Den Tag, an welchem alle diese Zahlen bereits existieren (also "ein Tag" nach abzählbar unendlich vielen Tagen) und wir mit diesen neue Zahlen erschaffen, nennen wir Tag ω. Wir werden sehen, dass sich nun auch Zahlen mit nicht endlichen Dezimaldarstellungen konstruieren lassen. Wir betrachten dazu:

Beispiel: Konstruktion von [math]\frac{1}{3}[/math]

Es soll hier zunächst die Konstruktionsidee skizziert werden, welche in ähnlicher Form in weiteren Konstruktionen angewandt werden wird:

Konstruktionsidee

Wir wollen erreichen, dass [math]x=\frac{1}{3} [/math]

Wir wissen, dass [math] X_L \lt x \lt X_R [/math] . Wir füllen nun also [math]X_L [/math] mit Zahlen, die kleiner sind als [math]\frac{1}{3}[/math] und [math]X_R [/math] mit entsprechend größeren. Wir benötigen also also zwei nach 1/3 konvergente Folgen in den bereits existenten Zahlen. Setze also [math]x= \{a_n \in (a)_n | b_n \in (b)_n\}[/math], wobei [math](a)_n[/math]eine monoton steigende und [math](b)_n[/math]eine monoton fallende Folge ist.

Ansatz

Setze

[math]a_n=\frac{(4^n-1)/3}{4^n}[/math]

und

[math]b_n=\frac{(2^{2n+1}+1)/3}{2^{2n+1}}[/math]

Man kann sich leicht überlegen, dass die Folgen die gewünschten Eigenschaften besitzen.

Da sich die reellen Zahlen vollständig durch Cauchyfolgen konstruieren lassen, ist somit ganz [math]\mathbb{R} [/math] an Tag ω erschaffen.

Konstruktion von hyperrellen Zahlen

An Tag ω werden aber nicht nur die Reellen Zahlen erschaffen, sondern ebenfalls infinitesmal benachtbarte und infinite Zahlen. Diese können mit solchen aus den hyperreellen Zahlen identifiziert werden.

Beispiel: Konstruktion von ε

Setze [math]a_n=\frac{1}{2^n}[/math]. Dann ist [math]\epsilon = \{ 0 | a_n \in (a)_n\}[/math]kleiner als jede positive Zahl, aber größer als Null, also eine infinitismal kleine Zahl. Durch Addition [math]x+\epsilon[/math] (oder subtraktion) lässt sich zu zu jeder Zahl x eine infinitismal benachtbarte Zahl schaffen.

Beachte, dass [math](a)_n[/math]eine beliebige Nulllfolge sein kann.

Beispiel: Konstruktion von ω

Setze [math]a_n=n[/math]. Dann ist [math]\omega = \{ a_n \in (a)_n| \}=\{ 1,2,3,4,...| \}[/math]offenbar größer als jede reelle Zahl.

Es ist desweiteren εω = 1, was hier gezeigt wird.

Rechnen mit surrealen Zahlen

Grundrechenarten

Die surrealen Zahlen erhalten mit den folgenden arithmetischen Operationen Körpereigenschaften (mit 0 als neutralem Element der Addition und 1 als neutralem Element der Multiplikation):

Zu [math]x = \{X_L|X_R\} [/math], [math]y = \{Y_L|Y_R\} [/math] definieren wir:

• [math]-x = - \{ X_L | X_R \} = \{ -X_R | -X_L \}[/math]
• [math]x + y = \{ X_L | X_R \} + \{ Y_L | Y_R \} = \{ X_L + y, x + Y_L | X_R + y, x + Y_R \}[/math] mit [math]X + y = \{ x + y: x \in X \} , x + Y = \{ x + y: y \in Y \}[/math]
• [math]x − y := x + (−y) [/math]
• [math]\begin{align} xy & = \{ X_L | X_R \} \{ Y_L | Y_R \} \\ & = \left\{ X_L y + x Y_L - X_L Y_L, X_R y + x Y_R - X_R Y_R | X_L y + x Y_R - X_L Y_R, x Y_L + X_R y - X_R Y_L \right\} \\ \end{align}[/math]
• [math]\frac xy = x \left( \frac 1y \right)[/math] mit [math]\frac 1y = \Bigg \{0, \frac{1+(y_R-y)(\frac1y)_L}{y_R}, \frac{1+(y_L-y)(\frac1y)_R}{y_L} \Bigg | \frac{1+(y_L-y)(\frac1y)_L}{y_L}, \frac{1+(y_R-y)(\frac1y)_R}{y_R} \Bigg \}[/math]

Rechenregeln

Die Rechenregeln sind analog zu den Rechenregeln für reelle Zahlen, es gilt zum Beispiel das Assoziativgesetz ([math](x + y) + z = x + (y + z)[/math]) oder auch Aussagen wie [math]x + 0 = x[/math]beziehungsweise [math]1 · y = y[/math].

(Beweise: siehe hier)

Spieltheorie

Spiele, die bestimmten Regeln folgen, lassen sich durch surreale Zahlen beschreiben. Für muss ein Spiel allerdings folgende Eigenschaften aufweisen:

• Es gibt nur zwei Spieler.
• Das Spiel ist deterministisch (kein Zufallseinfluss).
• Alle Informationen sind offen zugänglich.
• Die Spieler machen abwechselnd ihren Zug.
• Das Spiel endet nach einer endlichen Anzahl an Zügen mit dem Sieg eines Spielers.
• Kann ein Spieler keinen Zug mehr machen, verliert er und das Spiel endet.

Bekannte Beispiele für solche Spiele sind Schach, Mühle, Dame und Go.

Games

Verallgemeinert man die surrealen Zahlen, indem man die Bedingung, dass jedes Element aus [math]L [/math] kleiner ist als jedes Element aus [math]R [/math] weglässt, dann erhält man die Games.

Konstruktionsregel

Sind [math]L[/math] und [math]R[/math] zwei Mengen von Games, dann ist [math]\{ L | R \}[/math] ein Game.

Mit dieser Konstruktionsregel lässt sich ein Game konstruieren. Operationen, wie Vergleich, Äquivalenz, Addition, Negation und Multiplikation sind genauso wie für surreale Zahlen definiert.

Da Games eine größere Klasse von Objekten als die surrealen Zahlen definiert, ist jede surreale Zahl auch ein Game. Eine später noch wichtige Eigenschaft der Games ist, dass ein Game entweder größer, gleich, kleiner als [math]0[/math] oder unvergleichbar (später auch fuzzy genannt) mit [math]0[/math] ist.

Anwendung auf Spiele

Nimmt man an, dass beide Spieler sich in einer bestimmten Spielsituation befinden (Game: [math]x[/math]), dann steht der Ausgang des Spiels fest:

• [math]x\gt 0[/math]Links gewinnt unabhängig davon, wer den nächsten Zug macht.
• [math]x\lt 0[/math]Rechts gewinnt unabhängig davon, wer den nächsten Zug macht.
• [math]x=0[/math]Der Spieler, der am Zug ist, verliert das Spiel.
• [math]x[/math]fuzzy Der Spieler, der am Zug ist, gewinnt das Spiel.

Teilpartien

Viele Spiele können nicht von Anfang an vollständig analysiert werden, zerfallen aber nach einigen Runden in voneinander unabhängige Teilspiele, die jeweils vollständig analysiert werden können (Bsp.: Endspiele bei Go). Um aus mehreren Teilpartien Rückschlüsse auf das gesamte Spiel zu ziehen lässt sich folgendes Theorem anwenden:

Wenn eine große Partie in zwei kleinere, unabhängige Partien zerfällt und die beiden Partien die Games [math]x[/math] und [math]y[/math] haben, dann hat die große Partie das Game [math]x+y[/math].

So lassen sich aus den Games Teilpartien erschließen, wie der Ausgang des gesamten Spiels aussieht.