Gegenbeispiele der Funktionentheorie und Analysis

Diese Seite untersucht Gegenbeispiele in den mathematischen Teilgebieten "Funktionentheorie" und "Analysis".

Der Abschnitt Gegenbeispiele der Analysis führt in das Studium der bekanntesten Gegenbeispiele der Analysis ein, und zeigt, welche pathologischen Eigenschaften diese jeweils haben.

In den Abschnitten, die sich mit der Funktionentheorie beschäftigen, wird insbesondere auf die Unterschiede zwischen komplexer Differenzierbarkeit und totaler, reeller Differenzierbarkeit eingegangen. Hierfür werden einige besondere Eigenschaften komplex-differenzierbarer (holomorpher) Funktionen formuliert, und reelle Gegenbeispiele, für welche diese Aussagen nicht gelten, gefunden.

Motivation

Die Untersuchung von Gegenbeispielen lässt sich unter anderem durch folgende drei Punkte motivieren:

• Gegenbeispiele können naheliegende und "intuitiv richtige" Aussage, die tatsächlich nicht gelten, widerlegen. So zeigt die Weierstraß-Funktion , dass Stetigkeit auf einem Intervall nicht Differenzierbarkeit in (irgend-)einem Punkt implizieren muss.
• Weiter können diese beweisen, dass zwei Definitionen verschieden sind, und, je nach Situation, möglicherweise auch, wodrin diese Unterschiede liegen. So zeigt die Indikatorfunktion der rationalen Zahlen (in den reellen Zahlen), die Lebesgue-integrierbar, aber nicht Riemann-integrierbar ist, dass diese beiden Definition der Integrierbarkeit/des Integrals nicht zusammenfallen können.
• Schließlich zeigen Gegenbeispiele (einer bestimmten Aussage) meist pathologische Sonderfälle auf, die durch geschickte Wahl der Definition und Voraussetzung der Aussage ausgeschlossen werden können.

Gegenbeispiele der Analysis

Neben der Funktionentheorie und der Topologie lassen sich auch in der Analysis viele Gegenbeispiele finden.

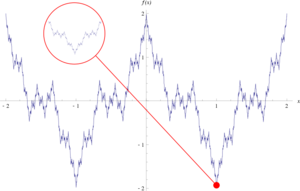
Die Weierstraß-Funktion

Der Graph einer Weierstraß-Funktion, die überall stetig, aber nirgendwo differenzierbar ist.

Die Weierstraß-Funktion [math]f:\mathbb{R} \rightarrow \mathbb{R}[/math] ist eine stetige Funktion, die in keinem Punkt differenzierbar ist.

Zur Definition wähle man [math]a \in (0,1)[/math] und [math]b \in \mathbb{N}[/math] ungerade, sodass [math]ab \gt 1 + \frac{3\pi}{2}[/math]. Dann ist die Weierstraß-Funktion durch [math]f: \mathbb{R} \rightarrow \mathbb{R}, x \mapsto \sum\limits_{n = 0}^{\infty} a^n \cos\left(b^n \pi x\right)[/math] gegeben.

Man kann zeigen, dass

1. die Weierstraß-Funktion [math]f[/math] stetig ist.
2. die Weierstraß-Funktion [math]f[/math] in keinem Punkt differenzierbar ist.

Beweis der Stetigkeit

Man betrachte die Weierstraß-Funktion als Funktionenreihe der Funktionen [math]\left(f_n: \mathbb{R} \rightarrow \mathbb{R}, x \mapsto a^n \cos\left(b^n\pi x\right)\right)_{n \in \mathbb{N}}[/math], die jeweils stetig in [math]x[/math] sind und der Abschätzung [math]|a^n \cos\left(b^n\pi x\right)| \leq |a^n| \leq a^n[/math] genügen. Als geometrische Reihe konvergiert [math]\sum\limits_{n = 0}^{\infty} a^n = \frac{1}{1 - a}[/math], sodass (über den Majorantensatz von Weierstraß) auch die Funktionenreihe [math]\sum\limits_{n = 0}^{\infty} a^n\cos\left(b^n\pi x\right)[/math] gleichmäßig auf [math]\mathbb{R}[/math] konvergiert. Nimmt man beide obigen Aussagen zusammen, so folgt bereits, dass die Weierstraß-Funktion als gleichmäßig konvergente Funktionsreihe stetiger Funktionen selbst stetig ist.

Beweis der Nicht-Differenzierbarkeit

Sei nun [math]x_0 \in \mathbb{R}[/math] ein beliebiger Punkt. Um zu zeigen, dass in diesem Punkt die Ableitung der Weierstraß-Funktion, also der Grenzwert [math]\lim\limits_{x \to x_0} \frac{f(x) - f(x_0)}{x - x_0}[/math], nicht existiert, reicht es eine Folge zu finden, die gegen [math]x_0[/math] konvergiert, während der dazugehörige Differenzenquotient keinen Grenzwert in [math]\mathbb{R}[/math] besitzt. Man wähle nun für jedes [math]m \in \mathbb{N}[/math] die eindeutige ganze Zahl [math]c_m \in \mathbb{Z}[/math], sodass [math]b^m x_0 - c_m \in \left(-\frac{1}{2}, \frac{1}{2}\right][/math] gilt. Weiter definiere man für jedes [math]m \in \mathbb{N}[/math] die reellen Zahlen [math]x_m := b^m x_0 - c_m[/math] und [math]y_m := \frac{c_m - 1}{b^m}[/math]. Für diese gelten die Ungleichung [math]y_m - x_0 = - \frac{1 + x_m}{b^m} \lt 0 [/math], also [math]y_m \lt x_0[/math]. Insbesondere folgt nun: [math]\lim\limits_{m \to \infty} |y_m - x_0| = \lim\limits_{m \to \infty} x_0 - y_m = \lim\limits_{m \to \infty} \frac{1 + x_m}{b^m} = 0[/math]. Die Folge [math](y_m)_{m \in \mathbb{N}}[/math] konvergiert also von unten gegen [math]x_0[/math]. Weiter gilt: [math]\phantom{=}\frac{f(y_m) - f(x_0)}{y_m - x_0} = \frac{\sum\limits_{n = 0}^{\infty}a^n\cos\left(b^n\pi y_m\right) - \sum\limits_{n = 0}^{\infty}a^n\cos\left(b^n\pi x_0\right)}{y_m - x_0} \\ = \sum\limits_{n = 0}^{\infty} a^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{y_m - x_0} \\ = \sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)} + \sum\limits_{n = m}^{\infty} a^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{y_m - x_0} \\ = \sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)} + \sum\limits_{n = 0}^{\infty} a^{n + m} \frac{\cos\left(b^{n + m}\pi y_m\right) - \cos\left(b^{n + m}\pi x_0\right)}{y_m - x_0} [/math]. Die erste Summe lässt sich nun mithilfe einer trigonometrischen Identität umformen; dann gilt: [math]\phantom{=}\sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)}\\ =\sum\limits_{n = 0}^{m - 1} \frac{-2(ab)^n }{b^n(y_m - x_0)}\sin\left(\frac{b^n\pi(y_m + x_0)}{2}\right)\sin\left(\frac{b^n\pi(y_m - x_0)}{2}\right) \\ = \sum\limits_{n = 0}^{m - 1}-\pi(ab)^n\sin\left(\frac{b^n\pi(y_m + x_0)}{2}\right)\frac{\sin\left(\frac{b^n\pi(y_m - x_0)}{2}\right)}{\frac{b^n\pi(y_m - x_0)}{2}} [/math]. Verwendet man nun die Dreiecks-Ungleichung und den Fakt, dass [math]\left|\frac{\sin(x)}{x}\right| \leq 1[/math] für alle [math]x \in \mathbb{R}\setminus\{0\}[/math], so ergibt sich weiter die Abschätzung: [math]\phantom{=}\left|\sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)}\right| \leq \sum\limits_{n = 0}^{m - 1}\pi (ab)^n = \pi\frac{(ab)^m - 1}{ab - 1} \lt \pi \frac{(ab)^m}{ab - 1}[/math]. Es existiert also ein [math]\epsilon \in (-1, 1)[/math], sodass [math]\sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)} = \epsilon \pi \frac{(ab)^m}{ab - 1}[/math]. Für die Terme in der zweiten Summe lassen sich folgende Vereinfachungen finden, wenn man beachtet, dass [math]b[/math] eine ungerade und [math]c_m[/math] eine beliebige ganze Zahl ist: [math]\cos\left(b^{n + m}\pi y_m\right) = \cos\left(b^n\pi (c_m - 1)\right) = (-1)^{b^n (c_m - 1)} = (-1)^{c_m - 1} = -(-1)^{c_m}[/math] Und mit dem trigonometrischen Additionstheorem für den Kosinus erhält man: [math]\cos\left(b^{n + m}\pi x_0\right) = \cos\left(b^n\pi(x_m + c_m)\right) = \cos\left(b^n\pi x_m\right)\cos\left(b^n \pi c_m\right) - \sin\left(b^n \pi x_m\right)\sin\left(b^n \pi c_m\right) = (-1)^{b^n c_m}\cos\left(b^n \pi c_m\right) - 0 = (-1)^{c_m}\cos\left(b^n\pi c_m\right)[/math]. Damit ergibt sich: [math]\phantom{=}\sum\limits_{n = 0}^{\infty} a^{n + m} \frac{\cos\left(b^{n + m}\pi y_m\right) - \cos\left(b^{n + m}\pi x_0\right)}{y_m - x_0} \\ = \sum\limits_{n = 0}^{\infty} a^{n + m} \frac{-(-1)^{c_m} - (-1)^{c_m}\cos\left(b^n\pi x_m\right)}{y_m - x_0} \\ = \sum\limits_{n = 0}^{\infty} a^{n + m}(-1)(-1)^{c_m} \frac{1 + \cos\left(b^n\pi x_m\right)}{-\frac{1 + x_m}{b^n}} \\ = (ab)^m(-1)^{c_m}\sum\limits_{n = 0}^{\infty} a^{n} \frac{1 + \cos\left(b^n\pi x_m\right)}{1 + x_m}. [/math] Beachtet man, dass [math]x_m \in \left(-\frac{1}{2}, \frac{1}{2}\right][/math], so folgt, dass alle Terme der obigen Summe positiv sind. Lässt man alle Terme für [math]n \geq 1[/math] weg, so ergibt sich die Abschätzung: [math]\phantom{=}\sum\limits_{n = 0}^{\infty} a^n \frac{1 + \cos\left(b^n\pi x_m\right)}{1 + x_m} \geq \frac{1 + \cos\left(\pi x_m\right)}{1 + x_m} \geq \frac{1}{1 + \frac{1}{2}} = \frac{2}{3}[/math], es gibt also ein [math]\eta \geq 1[/math], sodass [math](ab)^m(-1)^{c_m}\sum\limits_{n = 0}^{\infty} a^{n} \frac{1 + \cos\left(b^n\pi x_m\right)}{1 + x_m} = \frac{2}{3}(ab)^m(-1)^{c_m}\eta[/math]. Fügt man nun die Ausdrücke für beide Summen zusammen, so erhält man: [math]\phantom{=}\frac{f(y_m) - f(x_0)}{y_m - x_0} = \sum\limits_{n = 0}^{m - 1} (ab)^n \frac{\cos\left(b^n\pi y_m\right) - \cos\left(b^n\pi x_0\right)}{b^n(y_m - x_0)} + \sum\limits_{n = 0}^{\infty} a^{n + m} \frac{\cos\left(b^{n + m}\pi y_m\right) - \cos\left(b^{n + m}\pi x_0\right)}{y_m - x_0} = \epsilon\frac{\pi(ab)^m}{ab - 1} + \frac{2}{3}(ab)^m(-1)^{c_m}\eta = (-1)^{c_m}(ab)^m\eta\left(\frac{2}{3} + (-1)^{c_m}\frac{\epsilon}{\eta}\frac{\pi}{ab - 1}\right)[/math]. Erinnert man sich, dass [math]a[/math] und [math]b[/math] so gewählt wurden, dass [math]ab \gt 1 + \frac{3\pi}{2} \iff \frac{\pi}{ab - 1} = \frac{2}{3}[/math] und weiter [math]|\epsilon| \lt 1 [/math] und [math]\eta \geq 1[/math] gelten, so ergibt sich: [math]\phantom{=}\frac{2}{3} + (-1)^{c_m}\frac{\epsilon}{\eta}\frac{\pi}{ab - 1} \gt \frac{2}{3} - \frac{\pi}{ab - 1} \gt 0[/math]. Insbesondere folgt: [math]\phantom{=}\left|\frac{f(y_m) - f(x_0)}{y_m - x_0}\right| \gt (ab)^m\left(\frac{2}{3} - \frac{\pi}{ab - 1}\right) \rightarrow \infty[/math], sodass [math]f[/math] nicht in [math]x_0[/math] differenzierbar sein kann. Da [math]x_0[/math] beliebig gewählt war, ist die Weierstraß-Funktion [math]f[/math] also nirgendwo differenzierbar.

Die modifizierte Dirichlet-Funktion

Graph der modifizierten Dirichlet-Funktion auf dem Intervall (0,1).

Eine weitere interessante Funktion, die das intuitive Verständnis der Stetigkeit herausfordert, ist die modifizierte Dirichlet-Funktion. Diese ist teilweise auch als thomaesche Funktion bekannt.

Diese ist definiert durch [math]g: \mathbb{R} \rightarrow \mathbb{R}, x \mapsto \begin{cases}\frac{1}{q} & \text{für } x = \frac{p}{q} \in \mathbb{Q} \\ 0 & \text{für } x \in \mathbb{R}\setminus\mathbb{Q} \end{cases}[/math], sodass die Funktion folgende sonderbaren Eigenschaften hat:

1. Sie ist in den rationalen Zahlen [math]\mathbb{Q}[/math] unstetig.
2. Sie ist in den irrationalen Zahlen [math]\mathbb{R}\setminus\mathbb{Q}[/math] stetig.

Beweis der Unstetigkeit in den rationalen Zahlen

Wir zeigen zuerst die Unstetigkeit in den rationalen Zahlen. Dafür sei [math]x \in \mathbb{Q}[/math] eine beliebige rationale Zahl, sowie [math]p \in \mathbb{Z}, q \in \mathbb{N}[/math] die (eindeutigen) teilerfremden ganzen Zahlen, sodass [math]x = \frac{p}{q}[/math]. Damit gilt dann: [math]g(x_0) = \frac{1}{q}[/math]. Sei nun [math]0 \lt \epsilon \leq \frac{1}{q}[/math]. Es ist bekannt, dass für jedes [math]\delta \in \mathbb{R}_{\gt 0}[/math] unendlich viele irrationale Zahlen in der Umgebung [math]U_\delta (x_0) = (x_0 - \delta, x_0 + \delta)[/math] liegen. Für eine beliebige irrationale Zahl [math]x \in U_\delta (x_0) \cap \mathbb{R}\setminus\mathbb{Q}[/math] gilt nun: [math]|f(x_0) - f(x)| = |\frac{1}{q} - 0| = \frac{1}{q} \geq \varepsilon[/math]. Da [math]\delta[/math] beliebig gewählt war, kann [math]g[/math] nicht stetig in [math]x_0[/math] sein. Da [math]x_0[/math] beliebig gewählt war, ist nirgendwo in [math]\mathbb{Q}[/math] stetig.

Beweis der Stetigkeit in den irrationalen Zahlen

Nun zeigen wir, dass [math]g[/math] in den irrationalen Zahlen stetig ist. Sei dafür [math]x \in \mathbb{R}\setminus\mathbb{Q}[/math] eine beliebige irrationale Zahl und [math]\varepsilon \gt 0[/math]. Nun setze man [math]\delta_1 = \varepsilon[/math]. Weiter bezeichne [math]M_{\delta_1} := \{y \in (x_0 - \delta_1, x_0 + \delta_1) | \varepsilon \leq |g(y) - g(x_0)| = |g(y)|\}[/math] die Menge aller Punkte im Intervall [math](x_0 - \delta_1, x_0 + \delta_1)[/math], die die Stetigkeitsungleichung [math]|g(y) - g(x_0)| \leq \varepsilon[/math] nicht erfüllen. Per Konstruktion der Funktion [math]g[/math], gilt für die Menge [math]\mathbb{R}\setminus\mathbb{Q}[/math] der irrationalen Zahlen bereits, dass [math]g\left(\mathbb{R}\setminus\mathbb{Q}\right) \equiv 0[/math], also [math]M_{\delta_1} \subseteq \mathbb{Q}[/math]. Sei nun also [math]x = \frac{p}{q} \in M_{\delta_1} \subseteq \mathbb{Q}[/math]. Es gilt [math]\frac{1}{q} = g(x) = |g(x)| = |g(x) - g(x_0)| \geq \varepsilon[/math], also auch [math]q \leq \frac{1}{\varepsilon}[/math]. Da die Menge [math]N := \{n \in \mathbb{N} | n \leq \frac{1}{\varepsilon}\}[/math] offensichtlich endlich ist, können nur endlich viele Nenner [math]q_1, q_2, ..., q_n \in N[/math] in den (rationalen) Zahlen aus [math]M_{\delta_1}[/math] vorkommen. Da [math](x_0 - \delta_1, x_0 + \delta_1)[/math] beschränkt ist, können somit nur endlich viele rationale Zahlen mit Nennern [math]q_1, q_2, ..., q_n[/math] in [math](x_0 - \delta_1, x_0 + \delta_1)[/math] und somit in [math]M_{\delta_1}[/math] sein. Da [math]M_{\delta_1}[/math] in den rationalen Zahlen enthalten ist, ist [math]M_{\delta_1}[/math] somit endlich. Es kann also ohne Probleme ein [math]0 \lt \delta_0 \leq \delta_1[/math] gefunden werden, sodass [math](x_0 - \delta_0, x_0 + \delta_0) \cap M_{\delta_1} = \emptyset[/math]. Per Konstruktion von [math]M_{\delta_1}[/math] und [math]\delta_0[/math] gilt nun insbesondere, dass [math]g((x_0 - \delta_0, x_0 + \delta_0)) \subseteq (g(x_0) - \varepsilon, g(x_0) + \varepsilon)[/math]. Da [math]\varepsilon[/math] beliebig gewählt war, ist [math]g[/math] in [math]x_0[/math] stetig. Da [math]x_0[/math] beliebig (aus den irrationalen Zahlen [math]\mathbb{R}\setminus\mathbb{Q}[/math]) gewählt war, ist [math]g[/math] in den irrationalen Zahlen [math]\mathbb{R}\setminus\mathbb{Q}[/math] stetig.

Die Cantor-Funktion

Die Cantor-Funktion [math]f: [0,1] \rightarrow [0,1][/math] ist ein Funktion, die auf der ebenso unintuitiven Cantor-Menge [math]C \subset [0,1][/math] aufbaut und folgende Eigenschaften besitzt:

1. Sie ist monoton wachsend, beginnend bei [math]f(0) = 0[/math] und endend bei [math]f(1) = 1[/math].
2. Sie ist in den Punkten [math][0,1] \setminus C[/math] differenzierbar und ihre Ableitung besitzt dort jeweils den Wert [math]0[/math].

Die Indikatorfunktion der rationalen Zahlen

Ein letztes Gegenbeispiel der Analysis ist die Indikatorfunktion [math]\chi_{\mathbb{Q}}: \mathbb{R} \rightarrow \{0,1\}, x \mapsto \begin{cases}1 & \text{für } x \in \mathbb{Q} \\ 0 & \text{für } x \in \mathbb{R}\setminus\mathbb{Q}\end{cases}[/math] der rationalen Zahlen [math]\mathbb{Q}[/math] in den reellen Zahlen [math]\mathbb{R}[/math], welche die Unterschiedlichkeit der Lebesgue- und Riemann-Integrierbarkeit zeigt.

Denn für ebendiese Funktion [math]\chi_{\mathbb{Q}}[/math] lässt sich zeigen, dass sie:

1. Lebesgue-integrierbar ist.
2. nicht Riemann-integrierbar ist.

Beweis der Lebesgue-Integrierbarkeit

Nach der Definition des Lebesgue-Integrals gilt bereits: [math]\int_\mathbb{R} \chi_\mathbb{Q} \mathrm{d}\mathbb{\lambda} = \mathbb{\lambda}\left(\mathbb{Q}\right) = 0[/math]. Insbesondere ist [math]\chi_\mathbb{Q}[/math] also Lebesque-integrierbar.

Beweis der Nicht-Riemann-Integrierbarkeit

Bekanntermaßen impliziert die Riemann-Integrierbarkeit einer Funktion [math]f[/math], dass sie der gleichmäßige Grenzwert einer Folge [math](t_n)_{n \in \mathbb{N}}[/math] von Treppenfunktionen ist, also [math]\lim\limits_{n \rightarrow \infty}\|f - t_n\|_\infty = \lim\limits_{n \rightarrow \infty}\sup\limits_{x \in \mathbb{R}}|f(x) - t_n(x)| = 0[/math] gilt. Betrachtet man nun die Funktion [math]f = \chi_\mathbb{Q}[/math], so sieht man schnell ein, dass diese kein gleichmäßiger Grenzwert von Treppenfunktionen sein kann, da für jede beliebige Treppenfunktion mit beliebigen Stützpunkten und beliebigen Werten zwischen diesen Stützpunkten immer [math]\lim\limits_{n \rightarrow \infty}\|\chi_\mathbb{Q} - t_n\|_\infty \geq \frac{1}{2} \neq 0[/math] gilt. Dies liegt daran, dass in dem Intervall zwischen zwei Stützpunkten einer Treppenfunktion (auf dem die Treppenfunktion per Definition konstant einen Wert [math]w \in \mathbb{R}[/math] annimmt) jeweils eine rationale Zahl [math]x \in \mathbb{Q}[/math] und eine irrationale Zahl [math]y \in \mathbb{R}\setminus\mathbb{Q}[/math] mit [math]\chi_\mathbb{Q}(x) = 1[/math] und [math]\chi_\mathbb{Q}(y) = 0[/math] liegen. Offensichtlich gilt nun [math]max\{|\chi_\mathbb{Q}(x) - w|, |\chi_\mathbb{Q}(y) - w|\} \geq \frac{1}{2}[/math].

Holomorphe Funktionen

Motivation

In der eindimensionalen reellen Analysis definieren wir die Differenzierbarkeit einer Funktion [math]f\colon\mathbb{R} \to \mathbb{R}[/math] im Punkt [math]x_0[/math] über ihren Differenzenquotienten [math]\frac {f(x) - f(x_0)} {x-x_0}[/math].

Für mehrdimensionale Funktionen [math]f\colon\mathbb{R^n} \to \mathbb{R^m}[/math] ist dieser Ausdruck aber nicht mehr sinnvoll, da man hier durch einen Vektor [math]x-x_0 \in \mathbb{R^n}[/math] teilen würde. Daher benötigt man dort die Definition über das totale Differential.

Für den Spezialfall [math]f\colon\mathbb{R}^2 \to \mathbb{R}^2[/math] können wir jedoch auch [math]\mathbb{R}^2[/math] mit [math]\mathbb{C}[/math] identifizieren und die Körperstruktur von [math]\mathbb{C}[/math] nutzen. Dort ist also die Division durch [math]x-x_0 \in \mathbb{C}[/math] möglich, und wir erhalten mit dem klassischen Differenzenquotienten eine stärkere Art der Differenzierbarkeit, welche die Existenz eines totalen Differentials impliziert und darüber hinaus geht.

Definition

Sei [math]U\subseteq \mathbb{C}[/math] eine offene Teilmenge der komplexen Ebene. Eine Funktion [math]f\colon U \to \mathbb{C}[/math] heißt komplex differenzierbar im Punkt [math]z_0 \in U[/math], falls der Grenzwert [math]\lim \limits_{h \to 0}\frac{f(z_0+h)-f(z_0)}{h}[/math] existiert. Den Grenzwert bezeichnet man als [math]f'(z_0)[/math].

Ist [math]f[/math] in jedem Punkt [math]z \in U[/math] komplex differenzierbar, so heißt [math]f[/math] holomorph in [math]U[/math].

Ist [math]f[/math] auf ganz [math]\mathbb{C}[/math] komplex differenzierbar, so heißt [math]f[/math] ganze Funktion.

Beispiele

• [math]f\colon\mathbb{C} \to \mathbb{C}[/math], [math]z \rightarrow z^2+1[/math] ist ganz mit Ableitung [math]f'(z)=2z[/math]

Hierzu betrachte man den Differenzenquotienten:

[math]f'(z)=\lim \limits_{h \to 0}\frac{f(z+h)-f(z)}{h}=\lim \limits_{h \to 0}\frac{(z+h)^2+1-(z^2+1)}{h}=\lim \limits_{h \to 0}\frac{z^2+2zh+h^2+1-z^2-1}{h}=\lim \limits_{h \to 0}\frac{2zh+h^2}{h}=\lim \limits_{h \to 0}2z+h=2z[/math]

• Alle komplexen Polynome sind ganze Funktionen und es gelten die gleichen Ableitungsregeln wie in [math]\mathbb{R}[/math].

• Die reelle Exponentialfunktion und die trigonometrischen Funktionen [math]\sin[/math] und [math]\cos[/math] lassen sich auf eindeutige Weise zu ganzen Funktionen auf [math]\mathbb{C}[/math] fortsetzen.

Die Exponentialfunktion ist dabei definiert als [math]\exp(z):=e^{\text{Re}(z)}(\cos(\text{Im}(z))+i\sin(\text{Im}(z)))[/math]. Es gelten dann die aus dem Reellen bekannten Eigenschaften, z.B [math]\exp(x+y)=\exp(x)\exp(y)[/math] und [math]\exp'(z)=\exp(z)[/math].

Man sieht hier auch, dass die komplexe Exponentialfunktion eingeschränkt auf [math]\mathbb{R}[/math], genau die reelle Exponentialfunktion ist, da [math]\cos(0)+i\sin(0)=1[/math]

Der komplexe Sinus und der komplexe Cosinus sind dann wiederum durch die Exponentialfunktion definiert.

• Der reelle natürliche Logarithmus lässt sich eindeutig zu einer holomorphen Funktion auf dem Gebiet [math]\mathbb{C}\setminus\mathbb{R}^-_0[/math] fortsetzen.

• [math]z \rightarrow \text{Re}(z)[/math] und [math]z \rightarrow \text{Im}(z)[/math] sind in keinem Punkt [math]z \in \mathbb{C}[/math] komplex differenzierbar.

Differenzenquotient im Punkt [math]z[/math]:

[math]\lim \limits_{h \to 0}\frac{\text{Re}(z+h)-\text{Re}(z)}{h}=\lim \limits_{h \to 0}\frac{\text{Re}(h)}{h}[/math] existiert nicht, da der Grenzwert von der Wahl einer Folge für [math]h[/math] abhängt. Wähle für [math]h[/math] z.B die Folgen [math]a_n:=\frac{i}{n}[/math] und [math]b_n:=\frac{1}{n}[/math]. Es gilt [math]\text{Re}(a_n)=0[/math] und [math]\text{Re}(b_n)=b_n[/math], und daher

[math]\lim \limits_{n \to \infty}\frac{\text{Re}(a_n)}{a_n}=0[/math] und [math]\lim \limits_{n \to \infty}\frac{\text{Re}(b_n)}{b_n}=1[/math]

Dass die Projektionen auf Real- und Imaginärteil nicht holomorph sind, hat zur Folge, dass beliebige Verkettungen dieser im Allgemeinen auch nicht holomorph sind. Zum Beispiel der komplexe Betrag

[math]z\rightarrow |z|:=\sqrt{\text{Re}(z)^2+\text{Im}(z)^2}[/math] oder

[math]k(z):=\cos(\text{Re}(z))+i\cos(\text{Im}(z))[/math]

Totale Differenzierbarkeit

Definition

Sei [math]U\subseteq \mathbb{R}^2[/math] eine offene Teilmenge der reellen Ebene. Eine Funktion [math]f\colon U \to \mathbb{R}^2[/math] heißt (total) differenzierbar im Punkt [math]x_0[/math], falls eine lineare Abbildung [math]L\colon\mathbb{R}^2 \to \mathbb{R}^2[/math] existiert, so dass [math]\lim \limits_{h \to 0}\frac{f(x_0+h)-f(x_0)-L(h)}{||h||}=0[/math].

Die Abbildung [math]L[/math] wird als (totales) Differential von [math]f[/math] im Punkt [math]x_0[/math] bezeichnet.

Jacobi-Matrix

Wir schreiben eine Funktion [math]f\colon U \to \mathbb{R}^2[/math] mithilfe ihrer reellwertigen Komponenten [math]f_1, f_2\colon U \to \mathbb{R}[/math]

[math]f(x_1,x_2):= \left(\begin{array}{c} f_1(x_1,x_2) \\ f_2(x_1,x_2) \end{array}\right)[/math]

Die lineare Abbilidung [math]L[/math] ist durch die Jacobi-Matrix [math]J_f(x_0) := \left( \begin{array}{rr} \frac{\partial f_1}{\partial x_1}(x_0) & \frac{\partial f_1}{\partial x_2}(x_0) \\ \frac{\partial f_2}{\partial x_1}(x_0) & \frac{\partial f_2}{\partial x_2}(x_0) \\ \end{array}\right)[/math] gegeben, wobei [math]\frac{\partial f_i}{\partial x_j}[/math] die partiellen Ableitungen bezeichnen, also die Ableitung der reellwertigen Funktion [math]f_i[/math] nach der Variablen [math]x_j[/math].

Es gelten die folgenden Zusammenhänge:

• [math]f[/math] ist total differenzierbar auf [math]U \Rightarrow[/math] Alle partiellen Ableitungen existieren und [math]L[/math] ist eindeutig durch die Jacobi-Matrix gegeben.

• Alle partiellen Ableitungen von [math]f[/math] existieren und sind stetig auf [math]U \Rightarrow f[/math] ist total differenzierbar auf [math]U[/math]

Identifikation mit komplexwertigen Funktionen

Man kann nun die Komponenten [math]f_1[/math] und [math]f_2[/math] als Real- bzw. Imaginärteil einer komplexwertigen Funktion auffassen.

Sei [math]z:=z_1+iz_2 \in \mathbb{C}[/math].

[math]f(z):=f_1(z_1,z_2)+if_2(z_1,z_2)[/math] ist nun die entsprechende Funktion von [math]\mathbb{C}[/math] nach [math]\mathbb{C}[/math]. Diese kann man also auf Holomorphie untersuchen, und es stellt sich die Frage, wie die beiden Differenzierbarkeitsbegriffe zusammenhängen.

Direkter Vergleich

Beispiele

Wir fassen nun die im Abschnitt über Holomorphie diskutierten Beispiele [math]\quad f(z):=z^2+1,\quad \exp(z), \quad g(z):=\text{Re}(z), \quad h(z):=|z|=\sqrt{\text{Re}(z)^2+\text{Im}(z)^2}, \quad k(z):=\cos(\text{Re}(z))+i\cos(\text{Im}(z)), \quad[/math]als Funktionen von [math]\mathbb{R}^2[/math] nach [math]\mathbb{R}^2[/math] auf, und untersuchen sie auf totale Differenzierbarkeit.

Dazu schreiben wir [math]z=z_1+iz_2[/math] und berechnen die jeweiligen Real- und Imaginärteile:

• [math]\: f(z)=f(z_1+iz_2)=z_1^2+i^2z_2^2+2iz_1z_2+1=z_1^2-z_2^2+2iz_1z_2+1\\ \Rightarrow \text{Re}(f)=z_1^2-z_2^2+1,\quad \text{Im}(f)=2z_1z_2[/math]

• [math]\text{Re}(\exp(z))=e^{z_1}\cos(z_2), \quad \text{Im}(\exp)=e^{z_1}\sin(z_2)[/math]

• [math]\text{Re}(g(z))=z_1, \quad \text{Im}(g)=0[/math]

• [math]\text{Re}(h(z))=\sqrt{z_1^2+z_2^2}, \quad \text{Im}(h)=0[/math]

• [math]\text{Re}(k(z))=\cos(z_1), \quad \text{Im}(k)=\cos(z_2)[/math]

Die entsprechenden reellen Funktionen sind also:

• [math]f(x)=\left(\begin{array}{c} x_1^2-x_2^2+1 \\ 2x_1x_2 \end{array}\right)[/math]

• [math]\exp(x)=\left(\begin{array}{c} e^{x_1}\cos(x_2) \\ e^{x_1}\sin(x_2) \end{array}\right)[/math]

• [math]g(x)=\left(\begin{array}{c} x_1 \\ 0 \end{array}\right)[/math]

• [math]h(x)=\left(\begin{array}{c} \sqrt{x_1^2+x_2^2} \\ 0 \end{array}\right)[/math]

• [math]k(x)=\left(\begin{array}{c} \cos(x_1) \\ \cos(x_2) \end{array}\right)[/math]

Berechnen der partiellen Ableitungen liefert:

• [math]J_f(x) := \left( \begin{array}{rr} \frac{\partial f_1}{\partial x_1}(x) & \frac{\partial f_1}{\partial x_2}(x) \\ \frac{\partial f_2}{\partial x_1}(x) & \frac{\partial f_2}{\partial x_2}(x) \\ \end{array}\right)=\left( \begin{array}{rr} 2x_1 & -2x_2 \\ 2x_2 & 2x_1 \\ \end{array}\right)\\[/math]

Alle partiellen Ableitungen existieren und diese sind stetig auf ganz [math]\mathbb{R^2}[/math], [math]f[/math] ist dort also auch total differenzierbar. [math]f[/math] ist auch ganz.

• [math]J_{\exp}(x) = \left( \begin{array}{rr} \frac{\partial}{\partial x_1}(e^{x_1}\cos(x_2)) & \frac{\partial}{\partial x_2}(e^{x_1}\cos(x_2)) \\ \frac{\partial}{\partial x_1}(e^{x_1}\sin(x_2)) & \frac{\partial}{\partial x_2}(e^{x_1}\sin(x_2)) \\ \end{array}\right)=\left( \begin{array}{rr} e^{x_1}\cos(x_2) & -e^{x_1}\sin(x_2) \\ e^{x_1}\sin(x_2) & e^{x_1}\cos(x_2) \\ \end{array}\right)\\[/math]

Alle partiellen Ableitungen existieren und diese sind stetig auf ganz [math]\mathbb{R^2}[/math], [math]\exp[/math] ist dort also auch total differenzierbar. [math]\exp[/math] ist auch ganz.

• [math]J_g(x) := \left( \begin{array}{rr} \frac{\partial g_1}{\partial x_1}(x) & \frac{\partial g_1}{\partial x_2}(x) \\ \frac{\partial g_2}{\partial x_1}(x) & \frac{\partial g_2}{\partial x_2}(x) \\ \end{array}\right)=\left( \begin{array}{rr} 1 & 0 \\ 0 & 0 \\ \end{array}\right)\\[/math]

Alle partiellen Ableitungen existieren und diese sind stetig auf ganz [math]\mathbb{R^2}[/math], [math]g[/math] ist dort also auch total differenzierbar. [math]g[/math] ist in keinem Punkt komplex differenzierbar.

• [math]J_h(x) := \left( \begin{array}{rr} \frac{\partial h_1}{\partial x_1}(x) & \frac{\partial h_1}{\partial x_2}(x) \\ \frac{\partial h_2}{\partial x_1}(x) & \frac{\partial h_2}{\partial x_2}(x) \\ \end{array}\right)=\left( \begin{array}{rr} \frac{x_1}{\sqrt{x_1^2+x_2^2}} & \frac{x_2}{\sqrt{x_1^2+x_2^2}} \\ 0 & 0 \\ \end{array}\right)\\[/math]

Alle partiellen Ableitungen existieren auf [math]\mathbb{R^2}\setminus\lbrace 0\rbrace[/math] und sind dort stetig. [math]h[/math] ist also total differenzierbar auf [math]\mathbb{R^2}\setminus\lbrace 0\rbrace[/math], aber nicht holomorph. [math]h[/math] ist weder differenzierbar noch komplex differenzierbar in [math](0,0)[/math], da dort die partiellen Ableitungen nicht existieren.

• [math]J_k(x) := \left( \begin{array}{rr} \frac{\partial k_1}{\partial x_1}(x) & \frac{\partial k_1}{\partial x_2}(x) \\ \frac{\partial k_2}{\partial x_1}(x) & \frac{\partial k_2}{\partial x_2}(x) \\ \end{array}\right)=\left( \begin{array}{rr} -\sin(x_1) & 0 \\ 0 & -\sin(x_2) \\ \end{array}\right)[/math]

[math]k[/math] ist total differenzierbar auf [math]\mathbb{R^2}[/math], aber in keinem Gebiet holomorph.

Cauchy-Riemannsche partielle Differentialgleichungen

Die betrachteten Beispiele zeigen, dass aus totaler Differenzierbarkeit nicht unbedingt Holomorphie folgt. Sie lassen aber vermuten, dass holomorphe Funktionen auch total differenzierbar sind, und dass die Jacobimatrizen holomorpher Funktionen die spezielle Form [math]J = \left( \begin{array}{rr} a & -b \\ b & a \\ \end{array}\right)[/math] haben.

In der Tat kann man anhand der Definitionen mit einer elementaren Rechnung herleiten, dass die zu einer holomorphen Funktion gehörige reelle Auffassung total differenzierbar ist, und gleichzeitig die Cauchy-Riemannschen Differentialgleichungen erfüllt:

[math]\begin{align} \frac{\partial f_1}{\partial x_1}(x) &= \frac{\partial f_2}{\partial x_2}(x) & \qquad \\ \frac{\partial f_1}{\partial x_2}(x) &= -\frac{\partial f_2}{\partial x_1}(x) & \qquad \end{align}[/math]

Dies entspricht der oben genannten Form für die Jacobimatrix.

Die Umkehrung dieser Aussage gilt auch, und somit:

[math]f\colon \mathbb{C} \rightarrow \mathbb{C}[/math] ist holomorph auf dem Gebiet [math]U[/math] [math]\Longleftrightarrow f\colon \mathbb{R^2} \rightarrow \mathbb{R^2}[/math] ist total differenzierbar auf [math]U[/math] und erfüllt dort die Cauchy-Riemannschen Differentialgleichungen

Die Erfüllung der CR-DGL ist eine sehr starke Eigenschaft und führt zu einigen interessanten Implikationen, die im reellen kein Gegenstück besitzen. Die Menge der holomorphen Funktionen ist sehr "klein", in dem Sinne, dass sie sich bereits durch sehr wenige Informationen eindeutig identifizieren lassen.

Analytizität

Die Ableitung einer holomorphen Funktion ist wieder holomorph. Das bedeutet, dass jede holomorphe Funktion beliebig oft komplex differenzierbar ist.

Außerdem sind holomorphe Funktionen analytisch, das heißt sie lassen sich lokal durch eine konvergente Potenzreihe beschreiben.

Beide Aussagen sind im reellen falsch. Selbst im Falle einer unendlich oft differenzierbaren reellen Funktion, muss ihre Taylorreihe nicht unbedingt konvergieren.

Satz von Liouville

Der Satz von Liouville besagt, dass eine ganze Funktion (auf ganz [math]\mathbb{C}[/math] holomorphe Funktion), die auch beschränkt ist, bereits konstant sein muss.

Es gibt also keine beschränkten, ganzen Funktionen, die nicht konstant sind. Die beiden besprochenen Beispiele für ganze Funktionen, [math]f(z)=z^2+1[/math] und [math]\exp(z)[/math], sind beide unbeschränkt auf [math]\mathbb{C}[/math], da diese bereits auf den reellen Zahlen unbeschränkt sind.

Hierbei ist die Bedingung auf ganz [math]\mathbb{C}[/math] holomorph zu sein wichtig, der Satz gilt nicht für beliebige Gebiete [math]U\subseteq \mathbb{C}[/math], weder für beschränkte noch für unbeschränkte Gebiete.

Beispiel

Wir betrachten ein unbeschränktes Gebiet [math]U \subset \mathbb{C}[/math] und die Exponentialfunktion.

Die Exponentialfunktion ist [math]2\pi i[/math] -periodisch. Das ergibt sich aus ihrer Definition:

[math]\exp(z+2\pi i)=e^{\text{Re}(z+2\pi i)}(\cos(\text{Im}(z+2\pi i))+i\sin(\text{Im}(z+2\pi i)))=e^{z_1}(\cos(z_2+2\pi)+i\sin(z_2+2\pi))=e^{z_1}(\cos(z_2)+i\sin(z_2))=\exp(z)[/math]

Die Exponentialfunktion ist stetig und daher auf Kompakta beschränkt, somit ist sie auf dem Rechteck [math][0,1] \times [0,2\pi][/math] beschränkt. Wegen der Periodizität ist sie also auch auf dem unbeschränkten Gebiet [math]U=(0,1) \times (-\infty,\infty)[/math] beschränkt. Sie ist dort auch holomorph, aber kann dort nicht konstant sein, da sie bereits auf dem reellen Intervall [math](0,1)[/math] nicht konstant ist.

Beispiel

Um zu sehen, dass der Satz von Liouville im Reellen falsch ist, betrachten wir unser Beispiel [math]k(x):=\left(\begin{array}{c} \cos(x_1) \\ \cos(x_2) \end{array}\right)[/math]

Diese Funktion ist auf ganz [math]\mathbb{R^2}[/math] differenzierbar und außerdem beschränkt, da [math]\cos(x) \le 1[/math]. Sie ist aber nicht konstant.

Siehe auch

• Cantor-Funktion

Literatur

• Jürgen Appell: Analysis in Beispielen und Gegenbeispielen: Eine Einführung in die Theorie der reellen Zahlen, Springer-Verlag, Berlin [u.a.], 2009, ISBN 978-3-540-88902-1
• Bernard R. Gelbaum, John M. H. Olmsted: Counterexamples in Analysis, Dover Publications, Mineola.], 2003, ISBN 978-0486428758